Affine plads - Affine space

I matematik er et affin rum en geometrisk struktur, der generaliserer nogle af egenskaberne for euklidiske rum på en sådan måde, at disse er uafhængige af begreberne afstand og måling af vinkler, og kun bevarer egenskaberne relateret til parallelisme og forholdet mellem længder for parallel linjesegmenter .

I et affint rum er der ikke noget fornemt punkt, der tjener som oprindelse. Derfor har ingen vektor en fast oprindelse, og ingen vektor kan entydigt knyttes til et punkt. I et affint rum er der i stedet forskydningsvektorer , også kaldet oversættelsesvektorer eller blot oversættelser , mellem to punkter i rummet. Det er således fornuftigt at fratrække to punkter i rummet og give en oversættelsesvektor, men det giver ikke mening at tilføje to punkter i rummet. Det er ligeledes fornuftigt at tilføje en forskydningsvektor til et punkt i et affint rum, hvilket resulterer i et nyt punkt oversat fra startpunktet med den pågældende vektor.

Ethvert vektorrum kan ses som et affint rum; dette svarer til at glemme den særlige rolle, som nulvektoren spiller . I dette tilfælde kan elementerne i vektorrummet ses enten som punkter i det affine rum eller som forskydningsvektorer eller translationer . Når den betragtes som et punkt, kaldes nulvektoren for oprindelsen . Tilføjelse af en fast vektor til elementerne i et lineært underrum i et vektorrum frembringer et affint underrum . Man siger sædvanligvis, at dette affine underrum er opnået ved at oversætte (væk fra oprindelsen) det lineære underrum med oversættelsesvektoren. I endelige dimensioner er et sådant affint underrum løsningen af ​​et inhomogent lineært system. Forskydningsvektorerne for det affine rum er løsningerne af det tilsvarende homogene lineære system, som er et lineært underrum. Lineære underrum indeholder derimod altid oprindelsen af ​​vektorrummet.

Den dimension af en affin rum er defineret som dimension af vektorrum af sine oversættelser. Et affint rum af dimension et er en affin linje . Et affinrum af dimension 2 er et affineplan . Et affint underrum af dimension n - 1 i et affint rum eller et vektorrum af dimension n er et affint hyperplan .

Uformel beskrivelse

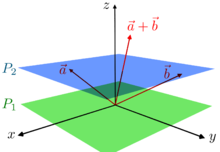
Den følgende karakterisering kan være lettere at forstå end den sædvanlige formelle definition: et affin rum er det, der er tilbage af et vektorrum, efter at du har glemt, hvilket punkt der er oprindelsen (eller, med den franske matematiker Marcel Bergers ord , "En affine space er ikke andet end et vektorrum, hvis oprindelse vi forsøger at glemme, ved at tilføje oversættelser til de lineære kort "). Forestil dig, at Alice ved, at et bestemt punkt er den faktiske oprindelse, men Bob mener, at et andet punkt - kald det p - er oprindelsen. To vektorer, a og b , skal tilføjes. Bob tegner en pil fra punkt p til punkt a og en anden pil fra punkt p til punkt b , og fuldender parallelogrammet for at finde, hvad Bob mener er a + b , men Alice ved, at han faktisk har beregnet

p + ( a - p ) + ( b - p ) .

På samme måde kan Alice og Bob evaluere enhver lineær kombination af a og b eller af et endeligt sæt vektorer og vil generelt få forskellige svar. Men hvis summen af ​​koefficienterne i en lineær kombination er 1, kommer Alice og Bob til det samme svar.

Hvis Alice rejser til

λ a + (1 - λ) b

så kan Bob på samme måde rejse til

p + λ ( a - p ) + (1 - λ) ( b - p ) = λ a + (1 - λ) b .

Under denne betingelse, for alle koefficienter λ + (1 - λ) = 1 , beskriver Alice og Bob det samme punkt med den samme lineære kombination, på trods af at de bruger forskellig oprindelse.

Selvom kun Alice kender den "lineære struktur", kender både Alice og Bob "affinestrukturen" - dvs. værdierne for affine kombinationer , defineret som lineære kombinationer, hvor summen af ​​koefficienterne er 1. Et sæt med en affin struktur er et affine plads.

Definition

En affin rum er et sæt A sammen med et vektorrum , og en transitiv og frie handling af den additive gruppe af på sættet A . Elementerne i affinrummet A kaldes punkter . Vektorrummet siges at være forbundet med det affine rum, og dets elementer kaldes vektorer , translationer eller undertiden frie vektorer . ${\ displaystyle {\ overrightarrow {A}}}$${\ displaystyle {\ overrightarrow {A}}}$${\ displaystyle {\ overrightarrow {A}}}$

Eksplicit betyder definitionen ovenfor, at handlingen er en kortlægning, generelt betegnet som en tilføjelse,

${\ displaystyle {\ begin {align} A \ times {\ overrightarrow {A}} & \ to A \\ (a, v) \; & \ mapsto a+v, \ end {align}}}$

der har følgende egenskaber.

1. Den rigtige identitet:

   ${\ displaystyle \ forall a \ i A, \; a+0 = a}$, hvor 0 er nulvektoren i${\ displaystyle {\ overrightarrow {A}}}$

2. Associativitet:

   ${\ displaystyle \ forall v, w \ in {\ overrightarrow {A}}, \ forall a \ in A, \; (a+v)+w = a+(v+w)}$(her er det sidste + tilføjelsen i )${\ displaystyle {\ overrightarrow {A}}}$

3. Gratis og transitiv handling:

   For hver er kortlægningen en bijection .${\ displaystyle a \ i A}$${\ displaystyle {\ overrightarrow {A}} \ til A \ colon v \ mapsto a+v}$

De to første egenskaber er simpelthen definerende egenskaber for en (højre) gruppeaktion. Den tredje egenskab karakteriserer frie og transitive handlinger, til -karakteren kommer fra transitivitet, og derefter følger den injektive karakter af, at handlingen er fri. Der er en fjerde ejendom, der følger af 1, 2 ovenfor:

4. Eksistensen af ​​en-til-en- oversættelser

For alle , kortlægningen er en bijektion.${\ displaystyle v \ in {\ overrightarrow {A}}}$${\ displaystyle A \ til A \ colon a \ mapsto a+v}$

Ejendom 3 bruges ofte i følgende tilsvarende form.

5. Subtraktion:

For hver a , b i A findes der en unik , betegnet b - a , sådan at .${\ displaystyle v \ in {\ overrightarrow {A}}}$${\ displaystyle b = a+v}$

En anden måde at udtrykke definitionen på er, at et affint rum er et principielt homogent rum for virkningen af ​​den additive gruppe af et vektorrum. Homogene rum er pr. Definition udstyret med en transitiv gruppeaktion, og for et principielt homogent rum er en sådan transitiv handling pr. Definition fri.

Subtraktion og Weyls aksiomer

Gruppeaktionens egenskaber muliggør definitionen af ​​subtraktion for ethvert givet ordnet par ( b , a ) punkter i A , der producerer en vektor af . Denne vektor, betegnet eller , er defineret til at være den unikke vektor i sådan ${\ displaystyle {\ overrightarrow {A}}}$${\ displaystyle ba}$${\ displaystyle {\ overrightarrow {ab}}}$${\ displaystyle {\ overrightarrow {A}}}$

${\ displaystyle a+(ba) = b.}$

Eksistens følger af handlingens transitivitet, og entydighed følger, fordi handlingen er gratis.

Denne subtraktion har de to følgende egenskaber, kaldet Weyls aksiomer:

1. ${\ displaystyle \ forall a \ in A, \; \ forall v \ in {\ overrightarrow {A}}}$, der er et unikt punkt sådan${\ displaystyle b \ i A}$${\ displaystyle ba = v.}$
2. ${\ displaystyle \ forall a, b, c \ i A, \; (cb)+(ba) = ca.}$

I euklidisk geometri kaldes det andet Weyls aksiom almindeligvis parallelogramreglen .

Affinierum kan defineres tilsvarende som et punktsæt A , sammen med et vektorrum og en subtraktion, der tilfredsstiller Weyls aksiomer. I dette tilfælde er tilføjelsen af ​​en vektor til et punkt defineret ud fra de første Weyls aksiomer. ${\ displaystyle {\ overrightarrow {A}}}$

Affinere delrum og parallelisme

Et affint underrum (også kaldet, i nogle sammenhænge, ​​en lineær variant , en flad eller, over de reelle tal , en lineær manifold ) B i et affin rum A er en delmængde af A, så set, givet et punkt , mængden af vektorer er et lineært underrum af . Denne egenskab, som ikke er afhængig af valget af a , indebærer, at B er et affin -rum, som har sit tilhørende vektorrum. ${\ displaystyle a \ i B}$${\ displaystyle {\ overrightarrow {B}} = \ {ba \ mid b \ i B \}}$${\ displaystyle {\ overrightarrow {A}}}$${\ displaystyle {\ overrightarrow {B}}}$

De affine underrum af A er formens undergrupper af A

${\ displaystyle a+V = \ {a+w: w \ i V \},}$

hvor a er et punkt på A , og V et lineært underrum af . ${\ displaystyle {\ overrightarrow {A}}}$

Det lineære underrum, der er forbundet med et affint underrum, kaldes ofte sit retning , og to underrum, der deler samme retning, siges at væreparallelle.

Dette indebærer følgende generalisering af Playfair s aksiom : Givet en retning V , for ethvert punkt en af A der er én og kun én affine underrum af retning V , som passerer gennem en , nemlig underrummet en + V .

Hver oversættelse kortlægger ethvert affint underrum til et parallelt underrum. ${\ displaystyle A \ til A: a \ mapsto a+v}$

Udtrykket parallel bruges også til to affine underrum, således at retning for den ene er inkluderet i den anden.

Affine kort

I betragtning af to affine mellemrum A og B, hvis tilknyttede vektorrum er og , er et affin kort eller affin homomorfisme fra A til B et kort ${\ displaystyle {\ overrightarrow {A}}}$${\ displaystyle {\ overrightarrow {B}}}$

${\ displaystyle f: A \ til B}$

sådan

${\ displaystyle {\ begin {align} {\ overrightarrow {f}}: {\ overrightarrow {A}} & \ to {\ overrightarrow {B}} \\ ba & \ mapsto f (b) -f (a) \ end {align}}}$

er et veldefineret lineært kort. Med at være veldefineret menes, at b - a = d - c indebærer f ( b ) - f ( a ) = f ( d ) - f ( c ) . ${\ displaystyle f}$

Dette indebærer, at man for et punkt og en vektor har ${\ displaystyle a \ i A}$${\ displaystyle v \ in {\ overrightarrow {A}}}$

${\ displaystyle f (a+v) = f (a)+{\ overpil {f}} (v).}$

Da b = a + v for et unikt v , for enhver given b i A , er f derfor fuldstændigt defineret af dens værdi på et enkelt punkt og det tilhørende lineære kort . ${\ displaystyle {\ overrightarrow {f}}}$

Vektorrum som affine rum

Hvert vektorrum V kan betragtes som et affint rum over sig selv. Dette betyder, at hvert element i V kan betragtes enten som et punkt eller som en vektor. Dette affine rum er undertiden betegnet ( V , V ) for at understrege den dobbelte rolle af elementerne i V . Når det betragtes som et punkt, betegnes nulvektoren sædvanligvis o (eller O , når store bogstaver bruges til punkter) og kaldes oprindelse .

Hvis A er et andet affint rum over det samme vektorrum (det vil sige ), vælger ethvert punkt a i A en unik affin isomorfisme, som er identiteten af V og kortlægger a til o . Med andre ord giver valget af en oprindelse a i A os mulighed for at identificere A og ( V , V ) op til en kanonisk isomorfisme . Modstykket til denne egenskab er, at affinrummet A kan identificeres med vektorrummet V , hvor "oprindelsesstedet er glemt". ${\ displaystyle V = {\ overpil {A}}}$

Forholdet til euklidiske rum

Definition af euklidiske rum

Euklidiske rum (herunder den endimensionelle linje, todimensionale plan og tredimensionelle rum, der sædvanligvis studeres i elementær geometri, samt højere-dimensionelle analoger) er affine rum.

I de fleste moderne definitioner er et euklidisk rum defineret til at være et affint rum, således at det tilhørende vektorrum er et reelt indre produktrum med en endelig dimension, det vil sige et vektorrum over realerne med en positiv-bestemt kvadratisk form q ( x ) . Det indre produkt af to vektorer x og y er værdien af ​​den symmetriske bilinære form

${\ displaystyle x \ cdot y = {\ frac {1} {2}} (q (x+y) -q (x) -q (y)).}$

Den sædvanlige euklidiske afstand mellem to punkter A og B er

${\ displaystyle d (A, B) = {\ sqrt {q (BA)}}.}$

I en ældre definition af euklidiske rum gennem syntetisk geometri er vektorer defineret som ækvivalensklasser af ordnede par punkter under ækvipollens (parene ( A , B ) og ( C , D ) er ækvipollente, hvis punkterne A , B , D , C ( i denne rækkefølge) danne et parallelogram ). Det er ligetil at kontrollere, at vektorerne danner et vektorrum, kvadratet i den euklidiske afstand er en kvadratisk form på vektors rum , og de to definitioner af euklidiske rum er ækvivalente.

Affine ejendomme

I euklidisk geometri refererer den almindelige sætning " affine property " til en egenskab, der kan bevises i affine rum, det vil sige, at den kan bevises uden at bruge den kvadratiske form og dens tilhørende indre produkt. Med andre ord er en affine ejendom en ejendom, der ikke involverer længder og vinkler. Typiske eksempler er parallelisme og definitionen af ​​en tangent . Et ikke-eksempel er definitionen på en normal .

Tilsvarende er en affin ejendom en ejendom, der er invariant under affine transformationer af det euklidiske rum.

Affine kombinationer og barycenter

Lad en ₁ , ..., en _n være en samling af n punkter i et affin rum, og være n elementer af jordfeltet . ${\ displaystyle \ lambda _ {1}, \ dots, \ lambda _ {n}}$

Antag det . For to punkter o og o ' har man ${\ displaystyle \ lambda _ {1} +\ dots +\ lambda _ {n} = 0}$

${\ displaystyle \ lambda _ {1} {\ overrightarrow {oa_ {1}}} +\ dots +\ lambda _ {n} {\ overrightarrow {oa_ {n}}} = \ lambda _ {1} {\ overrightarrow { o'a_ {1}}} +\ dots +\ lambda _ {n} {\ overrightarrow {o'a_ {n}}}.}$

Denne sum er således uafhængig af valget af oprindelse, og den resulterende vektor kan betegnes

${\ displaystyle \ lambda _ {1} a_ {1} +\ dots +\ lambda _ {n} a_ {n}.}$

Når , man henter definitionen af ​​subtraktion af punkter. ${\ displaystyle n = 2, \ lambda _ {1} = 1, \ lambda _ {2} =-1}$

Antag nu i stedet, at feltelementerne tilfredsstiller . For nogle valg af en oprindelse o , betegnes med det unikke punkt sådan, at ${\ displaystyle \ lambda _ {1} +\ dots +\ lambda _ {n} = 1}$${\ displaystyle g}$

${\ displaystyle \ lambda _ {1} {\ overrightarrow {oa_ {1}}} +\ dots +\ lambda _ {n} {\ overrightarrow {oa_ {n}}} = {\ overrightarrow {og}}.}$

Man kan vise, at det er uafhængigt af valget af o . Derfor, hvis ${\ displaystyle g}$

${\ displaystyle \ lambda _ {1} +\ dots +\ lambda _ {n} = 1,}$

kan man skrive

${\ displaystyle g = \ lambda _ {1} a_ {1} +\ dots +\ lambda _ {n} a_ {n}.}$

Pointen kaldes barycenter af for vægtene . Man siger også, at det er en affin kombination af de med koefficienter . ${\ displaystyle g}$${\ displaystyle a_ {i}}$${\ displaystyle \ lambda _ {i}}$${\ displaystyle g}$${\ displaystyle a_ {i}}$${\ displaystyle \ lambda _ {i}}$

Eksempler

• Når børn finde svar på beløb såsom 4 + 3 eller 4 - 2 ved at tælle til højre eller venstre på en række linje , de behandler nummeret linje som en endimensional affin plads.
• Enhver coset af et underrum V i et vektorrum er et affint rum over dette underrum.
• Hvis T er en matrix og b ligger i dets søjlerum , er mængden af ​​løsninger i ligningen T x = b et affint rum over underrummet af løsninger på T x = 0 .
• Løsningerne af en inhomogen lineær differentialligning danner et affin rum over løsningerne af den tilsvarende homogene lineære ligning.
• Generalisering af alt det ovenstående, hvis T  : V → W er en lineær kortlægning og y ligger i sit billede, er sæt af løsninger x ∈ V til ligningen T x = y en coset af kernen af T  , og er derfor en affine rum i Ker  T  .
• Pladsen for (lineære) komplementære underrum af et vektordelrum V i et vektorrum W er et affint rum over Hom ( W / V , V ) . Det vil sige, at hvis 0 → V → W → X → 0 er en kort nøjagtig sekvens af vektorrum, så bærer rummet for alle opdelinger i den nøjagtige sekvens naturligvis strukturen af ​​et affint rum over Hom ( X , V ) .

Affine spændvidde og baser

For enhver delmængde X af en affin rum A , der er en mindste affin underrum, der indeholder det, kaldet affine span af X . Det er skæringspunktet mellem alle affine underrum indeholder X , og dens retning er skæringspunktet mellem retningerne af affine underrum, der indeholder X .

Den affine span X er mængden af alle (finite) affin kombinationer af point fra X , og dens retning er den lineære span af x - y for x og y i X . Hvis man vælger et bestemt punkt x ₀ , retningen af affine span X er også den lineære span af x - x ₀ for x i X .

Man siger også, at den affine span X er genereret af X , og at X er et genererende sæt af sin affine span.

Et sæt X af punkter i et affint rum siges at væreaffinely uafhængig eller simpelthenuafhængig, hvis affin spændvidde for enstreng delmængdeaf X er en streng delmængde af X 's affine span. Anaffin basis ellerbarycentrisk ramme(se§ Barycentriske koordinaternedenfor) for et affin rum er et genereringssæt, der også er uafhængigt (det er et minimalt genererende sæt).

Husk, at dimensionen af et affint rum er dimensionen af ​​dets tilknyttede vektorrum. Baserne i et affin rum med endelig dimension n er de uafhængige delmængder af n + 1 elementer, eller tilsvarende de genererende undersæt af n + 1 elementer. Tilsvarende er { x ₀ , ..., x _n } et affint grundlag for et affint rum, hvis og kun hvis { x ₁ - x ₀ , ..., x _n - x ₀ } er et lineært grundlag for den tilhørende vektor plads.

Koordinater

Der er to stærkt relaterede former for koordinatsystemer, der kan defineres på affine rum.

Barycentriske koordinater

Lad A være en affin rum af dimension n over et felt k , og være en affin basis af A . Egenskaberne for et affint grundlag indebærer, at for hvert x i A er der en unik ( n + 1) - tuppel af elementer af k, således at ${\ displaystyle \ {x_ {0}, \ dots, x_ {n} \}}$ ${\ displaystyle (\ lambda _ {0}, \ dots, \ lambda _ {n})}$

${\ displaystyle \ lambda _ {0} +\ dots +\ lambda _ {n} = 1}$

og

${\ displaystyle x = \ lambda _ {0} x_ {0} +\ dots +\ lambda _ {n} x_ {n}.}$

De kaldes de barycentriske koordinater for x over det affine grundlag . Hvis x _i ses som legemer, der har vægte (eller masser) , er punktet x dermed barycenter for x _i , og dette forklarer oprindelsen af ​​udtrykket barycentriske koordinater . ${\ displaystyle \ lambda _ {i}}$${\ displaystyle \ {x_ {0}, \ dots, x_ {n} \}}$${\ displaystyle \ lambda _ {i}}$

De barycentriske koordinater definerer en affin isomorfisme mellem affinrummet A og det affine underrum af k ^{n + 1} defineret af ligningen . ${\ displaystyle \ lambda _ {0} +\ dots +\ lambda _ {n} = 1}$

For affine mellemrum med uendelig dimension gælder den samme definition, idet der kun bruges begrænsede summer. Det betyder, at for hvert punkt er kun et begrænset antal koordinater ikke-nul.

Affinere koordinater

En affin ramme af et affin rum består af et punkt, kaldet oprindelse , og et lineært grundlag for det tilhørende vektorrum. Mere præcist, for et affint rum A med tilhørende vektorrum , tilhører oprindelsen o A , og det lineære grundlag er et grundlag ( v ₁ , ..., v _n ) af (for enkeltheden af ​​notationen betragter vi kun tilfælde af en endelig dimension, er den generelle sag lignende). ${\ displaystyle {\ overrightarrow {A}}}$${\ displaystyle {\ overrightarrow {A}}}$

For hvert punkt p i A er der en unik sekvens af elementer i jordfeltet, således at ${\ displaystyle \ lambda _ {1}, \ dots, \ lambda _ {n}}$

${\ displaystyle p = o+\ lambda _ {1} v_ {1}+\ dots+\ lambda _ {n} v_ {n},}$

eller tilsvarende

${\ displaystyle {\ overrightarrow {op}} = \ lambda _ {1} v_ {1} +\ dots +\ lambda _ {n} v_ {n}.}$

De kaldes affin koordinaterne for p over affin rammen ( o , v ₁ , ..., v _n ) . ${\ displaystyle \ lambda _ {i}}$

Eksempel: I euklidisk geometri er kartesiske koordinater affine koordinater i forhold til en orthonormal ramme , det vil sige en affin ramme ( o , v ₁ , ..., v _n ) således at ( v ₁ , ..., v _n ) er en ortonormalt grundlag .

Forholdet mellem barycentriske og affine koordinater

Barycentriske koordinater og affine koordinater er stærkt relaterede og kan betragtes som ækvivalente.

Faktisk givet en barycentrisk ramme

${\ displaystyle (x_ {0}, \ dots, x_ {n}),}$

man udleder straks den affine ramme

${\ displaystyle (x_ {0}, {\ overrightarrow {x_ {0} x_ {1}}}, \ dots, {\ overrightarrow {x_ {0} x_ {n}}}) = \ left (x_ {0} , x_ {1} -x_ {0}, \ prikker, x_ {n} -x_ {0} \ højre),}$

og hvis

${\ displaystyle \ left (\ lambda _ {0}, \ lambda _ {1}, \ dots, \ lambda _ {n} \ right)}$

er de barycentriske koordinater for et punkt over den barycentriske ramme, så er affinekoordinaterne for det samme punkt over den affine ramme

${\ displaystyle \ left (\ lambda _ {1}, \ dots, \ lambda _ {n} \ right).}$

Omvendt, hvis

${\ displaystyle \ left (o, v_ {1}, \ dots, v_ {n} \ right)}$

er en affin ramme, altså

${\ displaystyle \ left (o, o+v_ {1}, \ dots, o+v_ {n} \ right)}$

er en barycentrisk ramme. Hvis

${\ displaystyle \ left (\ lambda _ {1}, \ dots, \ lambda _ {n} \ right)}$

er affinitetskoordinaterne for et punkt over affinrammen, så er dets barycentriske koordinater over den barycentriske ramme

${\ displaystyle \ left (1- \ lambda _ {1}-\ dots-\ lambda _ {n}, \ lambda _ {1}, \ dots, \ lambda _ {n} \ right).}$

Derfor er barycentriske og affine koordinater næsten ækvivalente. I de fleste applikationer foretrækkes affine koordinater, idet de involverer færre koordinater, der er uafhængige. I de situationer, hvor de vigtige punkter i det undersøgte problem er affinitetsuafhængige, kan barycentriske koordinater imidlertid føre til enklere beregning, som i det følgende eksempel.

Eksempel på trekanten

Hodepunkterne i en ikke-flad trekant danner et affin grundlag for det euklidiske plan . De barycentriske koordinater tillader let karakterisering af elementerne i trekanten, der ikke involverer vinkler eller afstand:

Hjørner er punkterne for barycentriske koordinater (1, 0, 0) , (0, 1, 0) og (0, 0, 1) . Linjerne, der understøtter kanterne, er de punkter, der har en nulkoordinat. Selve kanterne er de punkter, der har en nulkoordinat og to ikke -negative koordinater. Det indre af trekanten er de punkter, hvis alle koordinater er positive. De medianer er de punkter, der har to lige store koordinater, og den geometriske tyngdepunkt er pointen med koordinaterne ( 1/3, 1/3, 1/3) .

Ændring af koordinater

Tilfælde af affine koordinater

Tilfælde af barycentriske koordinater

Egenskaber ved affine homomorfier

Matrix repræsentation

Billede og fibre

Lade

${\ displaystyle f \ colon E \ til F}$

være en affin homomorfisme, med

${\ displaystyle {\ overrightarrow {f}} \ colon {\ overrightarrow {E}} \ to {\ overrightarrow {F}}}$

som tilhørende lineært kort.

Den billede af f er den affine underrum f (E) af F , der har som associerede vektorrum. Da et affint rum ikke har et nulelement, har et affint homomorfisme ikke en kerne . For ethvert punkt x i f ( E ) er det inverse billede f ^–1 ( x ) af x imidlertid et affint underrum af E , af retning . Dette affine underrum kaldes fiberen af x . ${\ displaystyle {\ overrightarrow {f}} ({\ overrightarrow {E}})}$ ${\ displaystyle {\ overrightarrow {f}}^{-1} ({\ overrightarrow {F}})}$

Projektion

Et vigtigt eksempel er projektionen parallelt med en eller anden retning på et affint underrum. Betydningen af ​​dette eksempel ligger i det faktum, at euklidiske rum er affine rum, og at denne form for fremskrivninger er grundlæggende i euklidisk geometri .

Mere præcist, givet et affint rum E med tilhørende vektorrum , lad F være et affint underrum af retning , og D være et komplementært underrum af in (dette betyder, at hver vektor af kan nedbrydes på en unik måde som summen af ​​et element af og et element af D ). For hvert punkt x i E er dets fremskrivning til F parallelt med D det unikke punkt p ( x ) i F, således at ${\ displaystyle {\ overrightarrow {E}}}$${\ displaystyle {\ overrightarrow {F}}}$${\ displaystyle {\ overrightarrow {F}}}$${\ displaystyle {\ overrightarrow {E}}}$${\ displaystyle {\ overrightarrow {E}}}$${\ displaystyle {\ overrightarrow {F}}}$

${\ displaystyle p (x) -x \ i D.}$

Dette er en affin homomorfisme, hvis tilhørende lineære kort er defineret af ${\ displaystyle {\ overrightarrow {p}}}$

${\ displaystyle {\ overrightarrow {p}} (xy) = p (x) -p (y),}$

for x og y i E .

Billedet af dette fremspring er F , og dets fibre er underrummene retningsændringer D .

Kvoteplads

Selvom kerner ikke er defineret for affine mellemrum, er kvotientrum defineret. Dette skyldes, at "tilhørende den samme fiber af en affin homomorfisme" er et ækvivalensforhold.

Lad E være et affint rum, og D være et lineært underrum af det tilhørende vektorrum . Den kvotient E / D af E af D er kvotienten af E ved ækvivalensrelationen således at x og y er tilsvarende, hvis ${\ displaystyle {\ overrightarrow {E}}}$

${\ displaystyle xy \ i D.}$

Denne kvotient er et affint rum, der har som tilhørende vektorrum. ${\ displaystyle {\ overrightarrow {E}}/D}$

For hver affin homomorfisme er billedet isomorft i forhold til E -kvotienten ved kernen på det tilhørende lineære kort. Dette er den første isomorfisme -sætning for affine rum. ${\ displaystyle E \ til F}$

Affinere transformation

Aksiomer

Affinierum undersøges normalt ved analytisk geometri ved hjælp af koordinater eller tilsvarende vektorrum. De kan også studeres som syntetisk geometri ved at nedskrive aksiomer, selvom denne tilgang er meget mindre almindelig. Der er flere forskellige aksiomer til affin rum.

Coxeter (1969 , s. 192) aksiomatiserer det særlige tilfælde af affin geometri over realerne som ordnet geometri sammen med en affin form af Desargues sætning og et aksiom, der angiver, at der i et fly højst er en linje gennem et givet punkt, der ikke møder en given linje.

Affine -fly opfylder følgende aksiomer ( Cameron 1991 , kapitel 2): ​​(hvor to linjer kaldes parallelle, hvis de er ens eller uensartede):

• Enhver to forskellige punkter ligger på en unik linje.
• I betragtning af et punkt og en linje er der en unik linje, der indeholder punktet og er parallel med linjen
• Der findes tre ikke-kollinære punkter.

Udover affine fly over felter (eller delingsringe ) er der også mange ikke-desarguesiske fly, der opfylder disse aksiomer. ( Cameron 1991 , kapitel 3) giver aksiomer til højere dimensionelle affinrum.

Rent aksiomatisk affin geometri er mere generel end affine rum og behandles i en separat artikel .

Forhold til projektive rum

Affinierum er indeholdt i projektive rum . For eksempel kan et affineplan fås fra ethvert projektionsplan ved at fjerne en linje og alle punkterne på det, og omvendt kan ethvert affineplan bruges til at konstruere et projektivt plan som en lukning ved at tilføje en linje i det uendelige, hvis punkter svarer til ækvivalensklasser af parallelle linjer . Lignende konstruktioner holder i højere dimensioner.

Endvidere giver transformationer af projektivt rum, der bevarer affin rum (ækvivalent, der efterlader hyperplanet ved uendelig invariant som et sæt ) transformationer af affint rum. Omvendt strækker enhver affin lineær transformation sig entydigt til en projektiv lineær transformation, så affinegruppen er en undergruppe af den projektive gruppe . For eksempel er Möbius -transformationer (transformationer af den komplekse projektive linje eller Riemann -kugle ) affine (transformationer af det komplekse plan), hvis og kun hvis de fikser punktet i det uendelige .

Affinere algebraisk geometri

I algebraisk geometri defineres en affin sort (eller mere generelt et affin algebraisk sæt ) som delsættet af et affin rum, der er sættet af de fælles nuller i et sæt såkaldte polynomiske funktioner over affinrummet . For at definere en polynomisk funktion over affinrummet skal man vælge en affin ramme . Derefter er en polynomfunktion en funktion, så billedet af et hvilket som helst punkt er værdien af ​​en multivariat polynomfunktion af punktets koordinater. Da en ændring af affine koordinater kan udtrykkes ved lineære funktioner (mere præcist affine funktioner) i koordinaterne, er denne definition uafhængig af et bestemt valg af koordinater.

Valget af et system med affine koordinater for et affint rum af dimension n frem for et felt k inducerer en affin isomorfisme mellem og affin koordinatrummet k ⁿ . Dette forklarer, hvorfor mange lærebøger forenkling skriver og introducerer affine algebraiske sorter som de almindelige nuller af polynomfunktioner over k ⁿ . ${\ displaystyle \ mathbb {A} _ {k}^{n}}$ ${\ displaystyle \ mathbb {A} _ {k}^{n}}$ ${\ displaystyle \ mathbb {A} _ {k}^{n} = k^{n}}$

Da hele affine rum er det sæt af fælles nuller af polynomiet nul , affine rum er affine algebraisk sorter.

Ring af polynomiske funktioner

Ved definitionen ovenfor giver valget af en affin ramme i et affin rum mulighed for at identificere de polynomiske funktioner på med polynomier i n variabler, hvor den i variabel repræsenterer den funktion, der knytter et punkt til dets i koordinat. Det følger heraf, at sættet med polynomiske funktioner over er en k -algebra , betegnet , som er isomorf i forhold til polynomringen . ${\ displaystyle \ mathbb {A} _ {k}^{n}}$${\ displaystyle \ mathbb {A} _ {k}^{n}}$${\ displaystyle \ mathbb {A} _ {k}^{n}}$${\ displaystyle k \ venstre [\ mathbb {A} _ {k}^{n} \ højre]}$ ${\ displaystyle k \ venstre [X_ {1}, \ dots, X_ {n} \ højre]}$

Når man ændrer koordinater, ændres isomorfismen mellem og ændres i overensstemmelse hermed, og dette fremkalder en automorfisme af , som kortlægger hver ubestemt til et polynom af grad 1. Det følger heraf, at den samlede grad definerer en filtrering af , som er uafhængig af valget af koordinater. Den samlede grad definerer også en graduering , men det afhænger af valget af koordinater, da en ændring af affine koordinater kan kortlægge ubestemte på ikke- homogene polynomier . ${\ displaystyle k \ venstre [\ mathbb {A} _ {k}^{n} \ højre]}$${\ displaystyle k [X_ {1}, \ dots, X_ {n}]}$${\ displaystyle k \ venstre [X_ {1}, \ dots, X_ {n} \ højre]}$${\ displaystyle k \ venstre [\ mathbb {A} _ {k}^{n} \ højre]}$

Zariski topologi

Affinere mellemrum over topologiske felter , såsom de reelle eller de komplekse tal, har en naturlig topologi . Zariski -topologien, der er defineret for affine mellemrum over ethvert felt, tillader under alle omstændigheder brug af topologiske metoder. Zariski -topologi er den unikke topologi på et affint rum, hvis lukkede sæt er affine algebraiske sæt (det er sæt af de almindelige nuller af polynomfunktioner over det affine sæt). Da polynomiske funktioner over et topologisk felt er kontinuerlige, lukkes hvert Zariski -lukket sæt for den sædvanlige topologi, hvis der er nogen. Med andre ord, over et topologisk felt er Zariski -topologi grovere end den naturlige topologi.

Der er en naturlig indsprøjtningsfunktion fra en affin plads til sættet med primære idealer (det er spektret ) i dens ring af polynomfunktioner. Når affine koordinater er valgt, kortlægger denne funktion koordinatpunktet til det maksimale ideal . Denne funktion er en homeomorfisme (for Zariski -topologien i affinrummet og spektret af ringen af ​​polynomfunktioner) af affinrummet på funktionens billede. ${\ displaystyle \ left (a_ {1}, \ dots, a_ {n} \ right)}$ ${\ displaystyle \ left \ langle X_ {1} -a_ {1}, \ dots, X_ {n} -a_ {n} \ right \ rangle}$

Tilfældet med et algebraisk lukket jordfelt er især vigtigt i algebraisk geometri, fordi homeomorfismen ovenfor i dette tilfælde er et kort mellem affinrummet og sættet af alle maksimale idealer for funktionsringen (dette er Hilberts Nullstellensatz ).

Dette er udgangspunktet for skema -teorien om Grothendieck , som består i, for at studere algebraiske sorter, at betragte som "punkter", ikke kun punkterne i det affine rum, men også alle spektrets primære idealer. Dette tillader sammenlimning algebraisk sorter på en lignende måde som for manifolder , diagrammer er limet sammen for at opbygge en manifold.

Kohomologi

Som alle andre affinesorter kan lokale data om et affineret rum altid lappes sammen globalt: kohomologien i affin rum er triviel. Mere præcist for alle sammenhængende skiver F og heltal . Denne ejendom nyder også alle andre affine sorter . Men også alle de étale kohomologigrupper på affin rum er trivielle. Især hver linjebundel er triviel. Mere generelt indebærer Quillen -Suslin -sætningen, at hver algebraisk vektorgruppe over et affin rum er trivielt. ${\ displaystyle H^{i} \ left (\ mathbb {A} _ {k}^{n}, \ mathbf {F} \ right) = 0}$${\ displaystyle i> 0}$

Se også

• Affine skrog  - Mindste affine underrum, der indeholder et delsæt
• Kompleks affin rum  - Affinér plads over de komplekse tal
• Eksotisk affin rum  - Virkelig affin rum af jævn dimension, der ikke er isomorf til et komplekst affin rum
• Rum (matematik)  - Matematisk sæt med en ekstra struktur

Noter

Referencer

• Berger, Marcel (1984), "Affine spaces" , Problemer i geometri , Springer-Verlag, ISBN 978-0-387-90971-4
• Berger, Marcel (1987), Geometry I , Berlin: Springer, ISBN 3-540-11658-3
• Cameron, Peter J. (1991), Projective and polar spaces , QMW Maths Notes, 13 , London: Queen Mary and Westfield College School of Mathematical Sciences, MR  1153019
• Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2. udgave), New York: John Wiley & Sons , ISBN 978-0-471-50458-0, MR  0123930
• Dolgachev, IV ; Shirokov, AP (2001) [1994], "Affine space" , Encyclopedia of Mathematics , EMS Press
• Hartshorne, Robin (1977). Algebraisk geometri . Springer-Verlag . ISBN 978-0-387-90244-9. Zbl  0367.14001 .
• Nomizu, K .; Sasaki, S. (1994), Affine Differential Geometry (Ny red.), Cambridge University Press, ISBN 978-0-521-44177-3
• Snapper, Ernst; Troyer, Robert J. (1989), Metric Affine Geometry (Dover -udgaven, først udgivet i 1989 -red.), Dover Publications, ISBN 0-486-66108-3
• Reventós Tarrida, Agustí (2011), "Affine spaces", Affine Maps, Euclidean Motions and Quadrics , Springer, ISBN 978-0-85729-709-9