Bijection - Bijection
| Fungere |
|---|
| x ↦ f ( x ) |
| Eksempler på domæner og kodomener |
| Klasser/ejendomme |
| Konstruktioner |
| Generaliseringer |
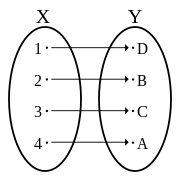
I matematik er en bijektion , bijektiv funktion , en-til-en-korrespondance eller inverterbar funktion en funktion mellem elementerne i to sæt , hvor hvert element i et sæt er parret med nøjagtigt et element i det andet sæt, og hvert element af det andet sæt er parret med præcis ét element i det første sæt. Der er ingen uparrede elementer. Matematisk, en bijektiv funktion f : X → Y er en en-til-en (injektiv) og på (Surjective) kortlægning af et sæt X til et sæt Y . Udtrykket en-til-en-korrespondance må ikke forveksles med en-til-en-funktion (en injektiv funktion ; se figurer).
En bijection fra sættet X til den indstillede Y har en omvendt funktion fra Y til X . Hvis X og Y er begrænsede sæt , betyder eksistensen af en bijektion, at de har det samme antal elementer. For uendelige sæt er billedet mere kompliceret, hvilket fører til begrebet kardinalnummer - en måde at skelne de forskellige størrelser af uendelige sæt på.
En bijektiv funktion fra et sæt til sig selv kaldes også en permutation , og sættet af alle permutationer af et sæt danner den symmetriske gruppe .
Bijektive funktioner er afgørende for mange matematikområder, herunder definitionerne af isomorfisme , homeomorfisme , diffeomorfisme , permutationsgruppe og projektivt kort .
Definition
For at en parring mellem X og Y (hvor Y ikke behøver at være forskellig fra X ) skal være en bijektion, skal fire egenskaber have:
- hvert element i X skal være parret med mindst et element af Y ,
- intet element i X må parres med mere end et element af Y ,
- hvert element i Y skal være parret med mindst et element af X og
- noget element af Y kan være parret med mere end et element af X .
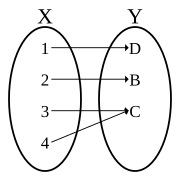
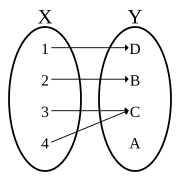
Opfylder egenskaber (1) og (2) betyder, at en parring er en funktion med domæne X . Det er mere almindeligt at se egenskaber (1) og (2) er skrevet som en enkelt sætning: Hvert element i X er parret med præcis ét element i Y . Funktioner, der tilfredsstiller egenskab (3) siges at være " på Y " og kaldes surjections (eller surjektive funktioner ). Funktioner, der opfylder egenskaben (4) siges at være " en-til-en-funktioner " og kaldes injektioner (eller injektive funktioner ). Med denne terminologi er en bijektion en funktion, der både er en overvejelse og en indsprøjtning, eller ved hjælp af andre ord, er en bijektion en funktion, der både er "en-til-en" og "på".
Bijections undertiden betegnet med en to-headed pil mod højre med hale ( U + 2916 ⤖ mod højre TO pil med hale ), som i f : X ⤖ Y . Dette symbol er en kombination af den tohovede pil mod højre ( U+ 21A0, HØJRE TO HEADED PIL ), nogle gange brugt til at betegne surjections, og pilen til højre med en pindehale ( U+ 21A3 ↣ HØJRE PIL MED HAL ), nogle gange brugt til at betegne injektioner.
Eksempler
Batting line-up af et baseball- eller crickethold
Overvej slagopstillingen for et baseball- eller crickethold (eller en liste over alle spillere på ethvert sportshold, hvor hver spiller har en bestemt plads i en line-up). Sættet X vil være spillerne på holdet (af størrelse ni i tilfælde af baseball) og sæt Y vil være positionerne i slagorden (1., 2., 3. osv.) "Parringen" er givet ved hvilken spilleren er i hvilken position i denne rækkefølge. Ejendom (1) er tilfreds, da hver spiller er et sted på listen. Ejendom (2) er tilfreds, da ingen spiller slår i to (eller flere) positioner i rækkefølgen. Ejendom (3) siger, at for hver position i rækkefølgen er der en spiller, der slår i den position, og ejendom (4) angiver, at to eller flere spillere aldrig slår på den samme position på listen.
Pladser og elever i et klasseværelse
I et klasseværelse er der et vist antal pladser. En flok elever kommer ind i lokalet, og instruktøren beder dem om at sidde. Efter et hurtigt kig rundt i rummet erklærer instruktøren, at der er en sammenføjning mellem elevsættet og sædesættet, hvor hver elev er parret med det sæde, de sidder i. Hvad instruktøren observerede for at nå frem til denne konklusion var det:
- Hver elev var på et sæde (der var ingen, der stod),
- Ingen studerende havde mere end ét sæde,
- Hvert sæde havde nogen siddende der (der var ingen tomme pladser), og
- Ingen plads havde mere end en elev i det.
Instruktøren kunne konkludere, at der var lige så mange pladser, som der var elever, uden at skulle tælle begge sæt.
Flere matematiske eksempler og nogle ikke-eksempler
- For ethvert sæt X er identitetsfunktionen 1 X : X → X , 1 X ( x ) = x bijektiv.
- Funktionen f : R → R , f ( x ) = 2 x + 1 er bijektiv, da der for hver y er en unik x = ( y - 1)/2, således at f ( x ) = y . Mere generelt er enhver lineær funktion over realerne f : R → R , f ( x ) = ax + b (hvor a er ikke-nul) en bijektion. Hvert reelt tal y er hentet fra (eller parret med) det reelle tal x = ( y - b )/ a .
- Funktionen f : R → (−π/2, π/2), givet ved f ( x ) = arctan ( x ) er bijektiv, da hvert reelt tal x er parret med nøjagtigt en vinkel y i intervallet (−π/ 2, π/2), så tan ( y ) = x (det vil sige y = arctan ( x )). Hvis codomain (−π/2, π/2) blev gjort større til at omfatte et heltal multiplum af π/2, ville denne funktion ikke længere være på (surjektiv), da der ikke er noget reelt tal, der kunne parres med multiplum af π/2 ved denne arctan -funktion.
- Den eksponentielle funktion , g : R → R , g ( x ) = e x , er ikke bijektiv: for eksempel er der ingen x i R, så g ( x ) = −1, hvilket viser, at g ikke er på (surjektiv) . Men hvis codomain er begrænset til de positive reelle tal , så ville g være bijektiv; dens omvendte (se nedenfor) er den naturlige logaritmefunktion ln.
- Funktionen h : R → R + , h ( x ) = x 2 er ikke bijektiv: for eksempel h (−1) = h (1) = 1, der viser, at h ikke er en-til-en (injektiv). Men hvis domænet er begrænset til , så ville h være bijektiv; dens omvendte er den positive kvadratrods funktion.
- Af Cantor-Bernstein-Schroder teorem , givet nogen to sæt X og Y , og to injektive funktioner f : X → Y og g : Y → X eksisterer der et bijektiv funktion h : X → Y .
Inverser
En bijektion f med domæne X (angivet med f : X → Y i funktionel notation ) definerer også en omvendt relation, der starter i Y og går til X (ved at dreje pilene rundt). Processen med "vende pilene omkring" til en vilkårlig funktion ikke, i almindelighed , udbytte en funktion, men egenskaber (3) og (4) af en bijection sige, at denne inverse relation er en funktion med domæne Y . Desuden siger egenskaber (1) og (2) så, at denne inverse funktion er en overvejelse og en injektion, det vil sige, at den inverse funktion eksisterer og også er en bijektion. Funktioner, der har inverse funktioner, siges at være inverterbare . En funktion er inverterbar, hvis og kun hvis det er en bijektion.
Angivet i kortfattet matematisk notation er en funktion f : X → Y bijektiv, hvis og kun hvis den opfylder betingelsen
- for hvert y i Y er der et unikt x i X med y = f ( x ).
Fortsat med baseball-batting line-up-eksemplet, den funktion, der defineres, tager som input navnet på en af spillerne og udsender placeringen af denne spiller i slagordren. Da denne funktion er en bijektion, har den en invers funktion, der som input indtager en position i slagordren og udsender den spiller, der vil slå i den position.
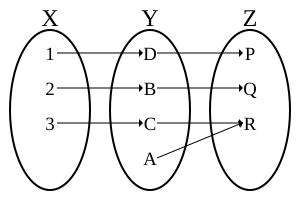
Sammensætning
Den sammensætning af to bijections f : X → Y og g : Y → Z er en bijection, hvis inverse er givet ved er .
Omvendt, hvis sammensætningen af to funktioner er bijektiv, følger det kun, at f er injektiv og g er subjektiv .
Kardinalitet
Hvis X og Y er begrænsede sæt , eksisterer der en bijection mellem de to sæt X og Y, hvis og kun hvis X og Y har samme antal elementer. I aksiomatisk sætteori betragtes dette faktisk som definitionen af "samme antal elementer" ( ækvivalensitet ), og generalisering af denne definition til uendelige sæt fører til begrebet kardinalnummer , en måde at skelne mellem de forskellige størrelser af uendelige sæt.
Ejendomme
- En funktion f : R → R er bijektiv, hvis og kun hvis grafen møder hver vandret og lodret linje nøjagtigt én gang.
- Hvis X er et sæt, danner den bijektive funktion fra X til sig selv sammen med funktionen af funktionel sammensætning (∘) en gruppe , den symmetriske gruppe af X , som betegnes forskelligt med S ( X ), S X eller X ! ( X factorial ).
- Bijections bevarer kardinaliteter i sæt: for en delmængde A af domænet med kardinalitet | A | og delmængde B af kodomenet med kardinalitet | B |, man har følgende ligheder:
- | f ( A ) | = | A | og | f −1 ( B ) | = | B |.
- Hvis X og Y er endelige sæt med samme kardinalitet og f : X → Y , er følgende ækvivalente:
- f er en bijection.
- f er en indsigelse .
- f er en injektion .
- Til et endeligt sæt S , der er en bijection mellem sættet af mulige samlede rækkefølger af elementerne og sættet af bijections fra S til S . Det vil sige, at antallet af permutationer af elementer i S er det samme som antallet af samlede bestillinger af dette sæt - nemlig n !.
Kategoriteori
Bijections er netop isomorfierne i kategorien Set af sæt og sætfunktioner . Imidlertid er sammenhængene ikke altid isomorfierne for mere komplekse kategorier. For eksempel i kategorien Grp af grupper skal morfismerne være homomorfismer, da de skal bevare gruppestrukturen, så isomorfierne er gruppeisomorfier, som er bijektive homomorfismer.
Generalisering til delfunktioner
Forestillingen om en-til-en-korrespondance generaliserer til delvise funktioner , hvor de kaldes partielle bijections , selvom partielle bijections kun kræves for at være injektive. Årsagen til denne lempelse er, at en (korrekt) delvis funktion allerede er udefineret for en del af sit domæne; der er således ingen overbevisende grund til at begrænse dens inverse til at være en total funktion , dvs. defineret overalt på sit domæne. Sættet af alle partielle bijections på et givet basesæt kaldes den symmetriske inverse semigruppe .
En anden måde at definere det samme begreb på er at sige, at en delvis bijektion fra A til B er enhver relation R (som viser sig at være en delvis funktion) med den egenskab, at R er grafen for en bijektion f : A ′ → B ′ , hvor a ' er en delmængde af a og B' er en delmængde af B .
Når den partielle bijektion er på det samme sæt, kaldes det undertiden en en-til-en delvis transformation . Et eksempel er Möbius -transformationen, der ganske enkelt er defineret på det komplekse plan, snarere end dens fuldførelse til det udvidede komplekse plan.
Se også
- Ax – Grothendieck sætning
- Bijection, injektion og overgivelse
- Bijektiv tal
- Bijective bevis
- Kategoriteori
- Funktion med flere værdier
Noter
Referencer
Dette emne er et grundlæggende begreb i sætteori og kan findes i enhver tekst, der indeholder en introduktion til sætteori. Næsten alle tekster, der omhandler en introduktion til at skrive beviser, vil indeholde et afsnit om sætteori, så emnet kan findes i nogen af disse:
- Wolf (1998). Bevis, logik og formodning: En matematikers værktøjskasse . Freeman.
- Sundstrom (2003). Matematisk ræsonnement: Skrivning og bevis . Prentice-Hall.
- Smith; Eggen; St.Andre (2006). En overgang til avanceret matematik (6. udgave) . Thomson (Brooks/Cole).
- Schumacher (1996). Kapitel Zero: Grundlæggende forestillinger om abstrakt matematik . Addison-Wesley.
- O'Leary (2003). Bevisstrukturen: Med logik og sætteori . Prentice-Hall.
- Morash. Bro til abstrakt matematik . Tilfældigt hus.
- Maddox (2002). Matematisk tænkning og skrivning . Harcourt/ Academic Press.
- Lay (2001). Analyse med introduktion til bevis . Prentice Hall.
- Gilbert; Vanstone (2005). En introduktion til matematisk tænkning . Pearson Prentice-Hall.
- Fletcher; Patty. Grundlaget for højere matematik . PWS-Kent.
- Iglewicz; Stoyle. En introduktion til matematisk ræsonnement . MacMillan.
- Devlin, Keith (2004). Sæt, funktioner og logik: En introduktion til abstrakt matematik . Chapman & Hall/ CRC Press.
- D'Angelo; West (2000). Matematisk tænkning: Problemløsning og beviser . Prentice Hall.
- Cupillari . Bevisernes møtrikker og bolte . Wadsworth.
- Bånd. Introduktion til abstrakt matematik . Brooks/Cole.
- Barnier; Feldman (2000). Introduktion til avanceret matematik . Prentice Hall.
- Aske. En primer af abstrakt matematik . MAA.