Centripetal kraft - Centripetal force

Del af en serie om
Klassisk mekanik
${\ displaystyle {\ textbf {F}} = {\ frac {d} {dt}} (m {\ textbf {v}})}$ Anden lov om bevægelse
Historie Tidslinje Lærebøger
Grene
Grundlæggende
Formuleringer
Kerneemner
Rotation
Forskere
Fysik portal  Kategori
v t e

En centripetal kraft (fra latinsk centrum , "center" og petere , "at søge") er en kraft, der får et legeme til at følge en buet vej . Dens retning er altid ortogonal i forhold til kroppens bevægelse og mod det faste punkt i det øjeblikkelige krumningscenter for stien. Isaac Newton beskrev det som "en kraft, hvormed kroppe bliver trukket eller skubbet eller på en eller anden måde har tendens til et punkt som til et centrum". I Newtons mekanik giver tyngdekraften den centripetalkraft, der forårsager astronomiske baner .

Et almindeligt eksempel, der involverer centripetalkraft, er det tilfælde, hvor et legeme bevæger sig med ensartet hastighed langs en cirkelbane. Centripetalkraften er rettet vinkelret på bevægelsen og også langs radius mod midten af ​​cirkelbanen. Den matematiske beskrivelse blev udledt i 1659 af den hollandske fysiker Christiaan Huygens .

Formel

Størrelsen af ​​centripetalkraften på et objekt med masse m, der bevæger sig med tangential hastighed v langs en sti med krumningsradius r er:

${\ displaystyle F_ {c} = ma_ {c} = {\ frac {mv^{2}} {r}}}$

${\ displaystyle a_ {c} = \ lim _ {\ Delta {t} \ to 0} {\ frac {| \ Delta {\ textbf {v}} |} {\ Delta {t}}}}$

hvor er centripetalacceleration og er forskellen mellem hastighedsvektorerne. Da hastighedsvektorerne i ovenstående diagram har en konstant størrelse, og da hver enkelt er vinkelret på sin respektive positionsvektor, indebærer enkel vektorsubtraktion to ens ensartede trekanter med kongruente vinkler - den ene omfatter en base af og en benlængde på , og den anden en basis af (position vektor forskel ) og en ben længde : ${\ displaystyle a_ {c}}$${\ displaystyle \ Delta {\ textbf {v}}}$${\ displaystyle \ Delta {\ textbf {v}}}$${\ displaystyle v}$${\ displaystyle \ Delta {\ textbf {r}}}$${\ displaystyle r}$

${\ displaystyle {\ frac {| \ Delta {\ textbf {v}} |} {v}} = {\ frac {| \ Delta {\ textbf {r}} |} {r}}}$

${\ displaystyle | \ Delta {\ textbf {v}} | = {\ frac {v} {r}} | \ Delta {\ textbf {r}} |}$

Derfor kan være substitueret med : ${\ displaystyle | \ Delta {\ textbf {v}} |}$${\ displaystyle {\ frac {v} {r}} | \ Delta {\ textbf {r}} |}$

${\ displaystyle a_ {c} = \ lim _ {{\ Delta} t \ to 0} {\ frac {| \ Delta {\ textbf {v}} |} {\ Delta {t}}} = {\ frac { v} {r}} \ lim _ {{\ Delta} t \ to 0} {\ frac {| \ Delta {\ textbf {r}} |} {\ Delta {t}}} = \ omega \ lim _ { {\ Delta} t \ to 0} {\ frac {| \ Delta {\ textbf {r}} |} {\ Delta {t}}} = v \ omega = {\ frac {v^{2}} {r }}}$

Kraftens retning er mod midten af ​​den cirkel, hvor objektet bevæger sig, eller den osculerende cirkel (den cirkel, der passer bedst til objektets lokale vej, hvis stien ikke er cirkulær). Hastigheden i formlen er kvadreret, så to gange hastigheden har brug for fire gange kraften. Det omvendte forhold til krumningsradius viser, at halvdelen af ​​den radiale afstand kræver dobbelt så stor kraft. Denne kraft er også undertiden skrevet i form af objektets vinkelhastighed ω omkring midten af ​​cirklen, relateret til tangentialhastigheden ved formlen

${\ displaystyle v = \ omega r}$

så det

${\ displaystyle F_ {c} = mr \ omega ^{2} \ ,.}$

Udtrykt ved hjælp af orbitalperioden T til en omdrejning af cirklen,

${\ displaystyle \ omega = {\ frac {2 \ pi} {T}} \,}$

ligningen bliver

${\ displaystyle F_ {c} = mr \ venstre ({\ frac {2 \ pi} {T}} \ højre)^{2}.}$

I partikelacceleratorer kan hastigheden være meget høj (tæt på lysets hastighed i vakuum), så den samme hvilemasse udøver nu større inerti (relativistisk masse) og kræver derved større kraft for den samme centripetale acceleration, så ligningen bliver:

${\ displaystyle F_ {c} = {\ frac {\ gamma mv^{2}} {r}}}$

hvor

${\ displaystyle \ gamma = {\ frac {1} {\ sqrt {1-{\ frac {v^{2}} {c^{2}}}}}}}}$

er Lorentz -faktoren .

Således er centripetalkraften givet ved:

${\ displaystyle F_ {c} = \ gamma mv \ omega}$

som er ændringshastigheden for relativistisk momentum . ${\ displaystyle \ gamma mv}$

Kilder

Et legeme, der oplever ensartet cirkulær bevægelse, kræver en centripetalkraft mod aksen som vist for at bevare sin cirkulære vej.

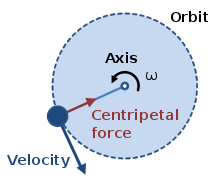
I tilfælde af et objekt, der svinger rundt på enden af ​​et reb i et vandret plan, tilføres centripetalkraften på objektet af rebets spænding. Rebeksemplet er et eksempel, der involverer en 'træk' kraft. Centripetalkraften kan også leveres som en "push" -kraft, f.eks. I det tilfælde, hvor en vægs normale reaktion forsyner centripetalkraften med en dødsfald eller en Rotor -rytter.

Newtons idé om en centripetal kraft svarer til det, der i dag omtales som en central kraft . Når en satellit er i kredsløb omkring en planet , anses tyngdekraften for at være en centripetalkraft, selvom gravitationskraften i tilfælde af excentriske baner er rettet mod fokus og ikke mod det øjeblikkelige krumningens centrum.

Et andet eksempel på centripetalkraft opstår i spiralen, der spores ud, når en ladet partikel bevæger sig i et ensartet magnetfelt i fravær af andre ydre kræfter. I dette tilfælde er den magnetiske kraft den centripetalkraft, der virker mod helixaksen.

Analyse af flere sager

Nedenfor er tre eksempler på stigende kompleksitet, med afledninger af formlerne, der styrer hastighed og acceleration.

Ensartet cirkulær bevægelse

Ensartet cirkulær bevægelse refererer til tilfælde af konstant rotationshastighed. Her er to tilgange til at beskrive denne sag.

Calculus -afledning

I to dimensioner kan positionsvektoren , der har størrelse (længde) og rettet i en vinkel over x-aksen, udtrykkes i kartesiske koordinater ved hjælp af enhedsvektorerne og : ${\ displaystyle {\ textbf {r}}}$${\ displaystyle r}$${\ displaystyle \ theta}$ ${\ displaystyle {\ hat {x}}}$${\ displaystyle {\ hat {y}}}$

${\ displaystyle {\ textbf {r}} = r \ cos (\ theta) {\ hat {x}}+r \ sin (\ theta) {\ hat {y}}.}$

Antag ensartet cirkulær bevægelse , hvilket kræver tre ting.

1. Objektet bevæger sig kun på en cirkel.
2. Cirkelens radius ændrer sig ikke med tiden.${\ displaystyle r}$
3. Objektet bevæger sig med konstant vinkelhastighed rundt om cirklen. Derfor, hvor er tiden.${\ displaystyle \ omega}$${\ displaystyle \ theta = \ omega t}$${\ displaystyle t}$

Find nu bevægelsens hastighed og acceleration ved at tage derivater af position med hensyn til tid. ${\ displaystyle {\ textbf {v}}}$ ${\ displaystyle {\ textbf {a}}}$

${\ displaystyle {\ textbf {r}} = r \ cos (\ omega t) {\ hat {x}}+r \ sin (\ omega t) {\ hat {y}}}$

${\ displaystyle {\ dot {\ textbf {r}}} = {\ textbf {v}} =-r \ omega \ sin (\ omega t) {\ hat {x}}+r \ omega \ cos (\ omega t) {\ hat {y}}}$

${\ displaystyle {\ ddot {\ textbf {r}}} = {\ textbf {a}} =-r \ omega ^{2} \ cos (\ omega t) {\ hat {x}}-r \ omega ^ {2} \ sin (\ omega t) {\ hat {y}}}$

${\ displaystyle {\ textbf {a}} =-\ omega ^{2} (r \ cos (\ omega t) {\ hat {x}}+r \ sin (\ omega t) {\ hat {y}} )}}$

Bemærk, at udtrykket i parentes er det originale udtryk for i kartesiske koordinater . Følgelig, ${\ displaystyle {\ textbf {r}}}$

${\ displaystyle {\ textbf {a}} =-\ omega ^{2} {\ textbf {r}}.}$

negativ viser, at accelerationen peger mod midten af ​​cirklen (modsat radius), derfor kaldes den "centripetal" (dvs. "center-seek"). Mens objekter naturligt følger en lige vej (på grund af inerti ), beskriver denne centripetalacceleration den cirkulære bevægelsesbane forårsaget af en centripetalkraft.

Afledning ved hjælp af vektorer

Vektorforhold til ensartet cirkulær bevægelse; vektor Ω, der repræsenterer rotationen, er normal for kredsløbets plan med polaritet bestemt af højre regel og størrelse dθ / dt .

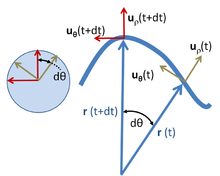
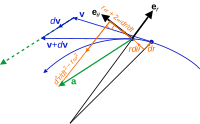
Billedet til højre viser vektorforholdene for ensartet cirkulær bevægelse. Selve rotationen repræsenteres af vinkelhastighedsvektoren Ω , som er normal i forhold til kredsløbets plan (ved hjælp af den højre regel ) og har størrelsen givet ved:

${\ displaystyle | \ mathbf {\ Omega} | = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} = \ omega \,}$

med θ vinkelpositionen på tidspunktet t . I dette underafsnit antages d θ /d t konstant, uafhængigt af tid. Den tilbagelagte afstand dℓ af partiklen i tiden d t langs cirkelbanen er

${\ displaystyle \ mathrm {d} {\ boldsymbol {\ ell}} = \ mathbf {\ Omega} \ times \ mathbf {r} (t) \ mathrm {d} t \,}$

som ved egenskaberne af vektorkrydsproduktet har størrelsen r d θ og er i retningen tangent til cirkelbanen.

Følgelig,

${\ displaystyle {\ frac {\ mathrm {d} \ mathbf {r}} {\ mathrm {d} t}} = \ lim _ {{\ Delta} t \ to 0} {\ frac {\ mathbf {r} (t+{\ Delta} t)-\ mathbf {r} (t)} {{\ Delta} t}} = {\ frac {\ mathrm {d} {\ boldsymbol {\ ell}}} {\ mathrm {d } t}} \.}$

Med andre ord,

${\ displaystyle \ mathbf {v} \ {\ stackrel {\ mathrm {def}} {=}} \ {\ frac {\ mathrm {d} \ mathbf {r}} {\ mathrm {d} t}} = { \ frac {\ mathrm {d} \ mathbf {\ boldsymbol {\ ell}}} {\ mathrm {d} t}} = \ mathbf {\ Omega} \ times \ mathbf {r} (t) \.}$

Differentiering med hensyn til tid,

${\ displaystyle \ mathbf {a} \ {\ stackrel {\ mathrm {def}} {=}} \ {\ frac {\ mathrm {d} \ mathbf {v}} {d \ mathrm {t}}} = \ mathbf {\ Omega} \ times {\ frac {\ mathrm {d} \ mathbf {r} (t)} {\ mathrm {d} t}} = \ mathbf {\ Omega} \ times \ left [\ mathbf {\ Omega} \ times \ mathbf {r} (t) \ right] \.}$

Lagranges formel siger:

${\ displaystyle \ mathbf {a} \ times \ left (\ mathbf {b} \ times \ mathbf {c} \ right) = \ mathbf {b} \ left (\ mathbf {a} \ cdot \ mathbf {c} \ højre)-\ mathbf {c} \ venstre (\ mathbf {a} \ cdot \ mathbf {b} \ højre) \.}$

Anvendelse af Lagranges formel med den observation, at Ω • r ( t ) = 0 til enhver tid,

${\ displaystyle \ mathbf {a} =-{| \ mathbf {\ Omega |}}^{2} \ mathbf {r} (t) \.}$

Med ord peger accelerationen til enhver tid direkte modsat radialforskydningen r og har en størrelse:

${\ displaystyle | \ mathbf {a} | = | \ mathbf {r} (t) | \ venstre ({\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} \ højre)^{ 2} = r {\ omega}^{2} \}$

hvor lodrette stænger | ... | betegne vektorstørrelsen, som i tilfælde af r ( t ) ganske enkelt er stiens radius r . Dette resultat stemmer overens med det foregående afsnit, selvom notationen er en smule anderledes.

Når rotationshastigheden gøres konstant i analysen af ikke -ensartet cirkulær bevægelse , stemmer denne analyse overens med denne.

En fordel ved vektormetoden er, at den er åbenbart uafhængig af ethvert koordinatsystem.

Eksempel: Den bankede sving

Øverste panel: Bold på et banket cirkulært spor, der bevæger sig med konstant hastighed v ; Nederste panel: Kræfter på bolden

Det øverste panel på billedet til højre viser en kugle i cirkulær bevægelse på en kurve. Kurven bankes i en vinkel θ fra vandret, og vejens overflade anses for at være glat. Målet er at finde, hvilken vinkel banken skal have, så bolden ikke glider af vejen. Intuition fortæller os, at bolden på en flad kurve uden bank overhovedet bare vil glide af vejen; med en meget stejl bank, vil bolden glide til midten, medmindre den bevæger kurven hurtigt.

Bortset fra enhver acceleration, der kan forekomme i banens retning, angiver billedets nederste panel kræfterne på bolden. Der er to kræfter; den ene er tyngdekraften lodret nedad gennem kuglens massecenter m g , hvor m er kuglens masse og g er tyngdeaccelerationen ; den anden er den normale opadgående kraft, der udøves af vejen i en ret vinkel i forhold til vejbanen m a _n . Den centripetalkraft, der kræves af den buede bevægelse, er også vist ovenfor. Denne centripetalkraft er ikke en tredje kraft, der påføres bolden, men skal snarere tilvejebringes af nettokraften på bolden som følge af vektortilsætning af den normale kraft og tyngdekraften . Den resulterende eller nettokraft på bolden fundet ved vektortilsætning af den normale kraft, der udøves af vejen, og lodret kraft på grund af tyngdekraften skal svare til centripetalkraften, der er dikteret af behovet for at rejse en cirkulær vej. Den buede bevægelse opretholdes, så længe denne nettokraft tilvejebringer den centripetalkraft, der er nødvendig for bevægelsen.

Den vandrette netkraft på bolden er den vandrette komponent af kraften fra vejen, som har størrelsen | F _h | = m | en _n | synd θ . Den lodrette komponent af kraften fra vejen skal modvirke tyngdekraften: | F _v | = m | a _n | cos θ = m | g |, hvilket indebærer | en _n | = | g | / cos θ . Substituerer til ovenstående formel for | F _h | giver en vandret kraft til at være:

${\ displaystyle | \ mathbf {F} _ {\ mathrm {h}} | = m | \ mathbf {g} | {\ frac {\ mathrm {sin} \ \ theta} {\ mathrm {cos} \ \ theta} } = m | \ mathbf {g} | \ mathrm {tan} \ \ theta \.}$

På den anden side ved hastighed | v | på en cirkulær bane med radius r siger kinematik, at den kraft, der er nødvendig for at vende bolden kontinuerligt ind i svinget, er den radialt indadgående centripetalkraft F _c af størrelsesorden:

${\ displaystyle | \ mathbf {F} _ {\ mathrm {c}} | = m | \ mathbf {a} _ {\ mathrm {c}} | = {\ frac {m | \ mathbf {v} |^{ 2}} {r}} \.}$

Følgelig er bolden i en stabil bane, når vejens vinkel er indstillet til at tilfredsstille betingelsen:

${\ displaystyle m | \ mathbf {g} | \ mathrm {tan} \ \ theta = {\ frac {m | \ mathbf {v} |^{2}} {r}} \,}$

eller,

${\ displaystyle \ mathrm {tan} \ \ theta = {\ frac {| \ mathbf {v} |^{2}} {| \ mathbf {g} | r}} \.}$

Som krængningsvinklen θ nærmer 90 °, den tangensfunktion nærmer uendelig, tillader større værdier for | v | ² / r . Med ord siger denne ligning, at for større hastigheder (større | v |) skal vejen bankes mere stejlt (en større værdi for θ ), og for skarpere sving (mindre r ) skal vejen også bankes mere stejlt, hvilket stemmer overens med intuition. Når vinklen θ ikke opfylder ovenstående betingelse, giver den vandrette kraftkomponent, der udøves af vejen, ikke den korrekte centripetalkraft, og en yderligere friktionskraft, der er tangential til vejoverfladen, opfordres til at give forskellen. Hvis friktion ikke kan gøre dette (dvs. friktionskoefficienten overskrides), glider bolden til en anden radius, hvor balancen kan realiseres.

Disse ideer gælder også for flyvning. Se FAA -pilotens manual.

Ujævn cirkulær bevægelse

Hastighed og acceleration for ikke -ensartet cirkulær bevægelse: Hastighedsvektoren er tangential til banen, men accelerationsvektoren er ikke radialt indad på grund af dens tangentielle komponent a _θ, der øger rotationshastigheden: d ω / dt = | en _θ | / R .

Som en generalisering af den ensartede cirkulære bevægelseskasse, antag at vinkelhastigheden ikke er konstant. Accelerationen har nu en tangential komponent, som vist på billedet til højre. Denne case bruges til at demonstrere en afledningsstrategi baseret på et polært koordinatsystem .

Lad r ( t ) være en vektor, der beskriver positionen af ​​en punktmasse som en funktion af tiden. Da vi antager cirkulær bevægelse , lad r ( t ) = R · u _r , hvor R er en konstant (cirkelens radius) og u _r er enhedsvektoren, der peger fra oprindelsen til punktmassen. Retningen af u _r er beskrevet af θ er vinklen mellem x-aksen og enhedsvektoren, målt mod uret fra x-aksen. Den anden enhedsvektor for polære koordinater, u _θ er vinkelret på u _r og peger i retning af stigende θ . Disse polare enhedsvektorer kan udtrykkes i form af kartesiske enhedsvektorer i x- og y -retningerne betegnet henholdsvis i og j :

u _r = cos θ i + sin θ j

og

u _θ = -sin θ i + cos θ j .

Man kan differentiere for at finde hastighed:

${\ displaystyle \ mathbf {v} = r {\ frac {\ mathrm {d} \ mathbf {u} _ {\ mathrm {r}}} {\ mathrm {d} t}} = r {\ frac {\ mathrm {d}} {\ mathrm {d} t}} \ venstre (\ mathrm {cos} \ \ theta \ \ mathbf {i} +\ mathrm {sin} \ \ theta \ \ mathbf {j} \ right)}$

${\ displaystyle = r {\ frac {d \ theta} {dt}} \ left (-\ mathrm {sin} \ \ theta \ \ mathbf {i} +\ mathrm {cos} \ \ theta \ \ mathbf {j} \ret)\,}$

${\ displaystyle = r {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {\ theta}} \,}$

${\ displaystyle = \ omega r \ mathbf {u} _ {\ mathrm {\ theta}} \,}$

hvor ω er vinkelhastigheden d θ /d t .

Dette resultat for hastigheden matcher forventningerne om, at hastigheden skal rettes tangentielt til cirklen, og at størrelsen af ​​hastigheden skal være rω . Differentierer igen, og bemærker det

${\ displaystyle {{\ frac {\ mathrm {d} \ mathbf {u} _ {\ mathrm {\ theta}}} {\ mathrm {d} t}} =-{\ frac {\ mathrm {d} \ theta } {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {r}} =-\ omega \ mathbf {u} _ {\ mathrm {r}}} \,}$

vi finder, at accelerationen, a er:

${\ displaystyle \ mathbf {a} = r \ venstre ({\ frac {\ mathrm {d} \ omega} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {\ theta}}-\ \ omega ^{2} \ mathbf {u} _ {\ mathrm {r}} \ right) \.}$

Således er accelerationens radiale og tangentielle komponenter:

${\ displaystyle \ mathbf {a} _ {\ mathrm {r}} =-\ omega ^{2} r \ \ mathbf {u} _ {\ mathrm {r}} =-{\ frac {| \ mathbf {v } |^{2}} {r}} \ \ mathbf {u} _ {\ mathrm {r}} \}$   og   ${\ displaystyle \ \ mathbf {a} _ {\ mathrm {\ theta}} = r \ {\ frac {\ mathrm {d} \ omega} {\ mathrm {d} t}} \ \ mathbf {u} _ { \ mathrm {\ theta}} = {\ frac {\ mathrm {d} | \ mathbf {v} |} {\ mathrm {d} t}} \ \ mathbf {u} _ {\ mathrm {\ theta}} \ ,}$

hvor | v | = r ω er størrelsen af ​​hastigheden (hastigheden).

Disse ligninger udtrykker matematisk, at i tilfælde af et objekt, der bevæger sig langs en cirkelbane med en skiftende hastighed, kan kroppens acceleration nedbrydes til en vinkelret komponent, der ændrer bevægelsesretningen (den centripetale acceleration) og en parallel eller tangential komponent , der ændrer hastigheden.

Generel plan bevægelse

Placer vektor r , peger altid radielt fra oprindelsen.

Hastighedsvektor v , der altid tangerer bevægelsesvejen.

Accelerationsvektor a , ikke parallel med den radiale bevægelse, men opvejet af vinkel- og Coriolis -accelerationerne, og heller ikke tangent til stien, men opvejet af centripetal- og radialaccelerationerne.

Kinematiske vektorer i plane polære koordinater. Bemærk, at opsætningen ikke er begrænset til 2d -rum, men et fly i enhver højere dimension.

Polare enhedsvektorer to gange t og t + dt for en partikel med bane r ( t ); til venstre flyttes enhedsvektorerne u _ρ og u _θ på de to tidspunkter, så deres haler alle mødes, og det vises at de sporer en bue af en enhedsradiuscirkel. Deres rotation i tiden dt er d θ, bare den samme vinkel som rotationen af ​​banen r ( t ).

Polære koordinater

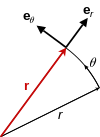
Ovenstående resultater kan måske afledes mere enkelt i polære koordinater og samtidig udvides til generel bevægelse inden for et plan, som vist nedenfor. Polare koordinater i planet anvender en radial enhedsvektor u _ρ og en vinkel enhedsvektor u _θ , som vist ovenfor. En partikel i position r er beskrevet af:

${\ displaystyle \ mathbf {r} = \ rho \ mathbf {u} _ {\ rho} \,}$

hvor notationen ρ bruges til at beskrive stiens afstand fra oprindelsen i stedet for R for at understrege, at denne afstand ikke er fast, men varierer med tiden. Enhedsvektoren u _ρ bevæger sig med partiklen og peger altid i samme retning som r ( t ). Enhedsvektor u _θ bevæger sig også med partiklen og forbliver ortogonal til u _ρ . Således u _p og u _Ø danne en lokal kartesisk koordinatsystem fæstnet til partiklen, og bundet til den bane af partiklen. Ved at flytte enhedsvektorerne, så deres haler falder sammen, som det ses i cirklen til venstre for billedet ovenfor, ses det, at u _ρ og u _θ danner et retvinklet par med spidser på enhedscirklen, der sporer frem og tilbage på omkredsen af ​​denne cirkel med samme vinkel θ ( t ) som r ( t ).

Når partiklen bevæger sig, er dens hastighed

${\ displaystyle \ mathbf {v} = {\ frac {\ mathrm {d} \ rho} {\ mathrm {d} t}} \ mathbf {u} _ {\ rho}+\ rho {\ frac {\ mathrm { d} \ mathbf {u} _ {\ rho}} {\ mathrm {d} t}} \.}$

For at evaluere hastigheden er derivatet af enhedsvektoren u _ρ nødvendig. Fordi u _ρ er en enhedsvektor, er dens størrelse fast, og den kan kun ændre sig i retning, det vil sige, at dens ændring d u _{ρ kun} har en komponent vinkelret på u _ρ . Når banen r ( t ) roterer en mængde d θ , roterer u _ρ , som peger i samme retning som r ( t ), også med d θ . Se billedet ovenfor. Derfor er ændringen i u _ρ er

${\ displaystyle \ mathrm {d} \ mathbf {u} _ {\ rho} = \ mathbf {u} _ {\ theta} \ mathrm {d} \ theta \,}$

eller

${\ displaystyle {\ frac {\ mathrm {d} \ mathbf {u} _ {\ rho}} {\ mathrm {d} t}} = \ mathbf {u} _ {\ theta} {\ frac {\ mathrm { d} \ theta} {\ mathrm {d} t}} \.}$

På lignende måde findes ændringshastigheden for u _θ . Som med u _ρ er u _θ en enhedsvektor og kan kun rotere uden at ændre størrelse. For at forblive ortogonal til u _ρ, mens banen r ( t ) roterer en mængde d θ , u _θ , som er ortogonal til r ( t ), roteres også med d θ . Se billedet ovenfor. Derfor er ændringen d u _θ ortogonal til u _θ og proportional med d θ (se billedet ovenfor):

${\ displaystyle {\ frac {\ mathrm {d} \ mathbf {u} _ {\ theta}} {\ mathrm {d} t}} =-{\ frac {\ mathrm {d} \ theta} {\ mathrm { d} t}} \ mathbf {u} _ {\ rho} \.}$

Billedet ovenfor viser tegnet at være negativ: at opretholde orthogonality, hvis d u _ρ er positiv med d θ , så d u _θ skal falde.

Substituerer derivatet af u _ρ i udtrykket for hastighed:

${\ displaystyle \ mathbf {v} = {\ frac {\ mathrm {d} \ rho} {\ mathrm {d} t}} \ mathbf {u} _ {\ rho}+\ rho \ mathbf {u} _ { \ theta} {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} = v _ {\ rho} \ mathbf {u} _ {\ rho}+v _ {\ theta} \ mathbf {u } _ {\ theta} = \ mathbf {v} _ {\ rho}+\ mathbf {v} _ {\ theta} \.}$

For at opnå accelerationen udføres en anden tidsdifferentiering:

${\ displaystyle \ mathbf {a} = {\ frac {\ mathrm {d} ^{2} \ rho} {\ mathrm {d} t ^{2}}} \ mathbf {u} _ {\ rho}+{ \ frac {\ mathrm {d} \ rho} {\ mathrm {d} t}} {\ frac {\ mathrm {d} \ mathbf {u} _ {\ rho}} {\ mathrm {d} t}}+ {\ frac {\ mathrm {d} \ rho} {\ mathrm {d} t}} \ mathbf {u} _ {\ theta} {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t }}+\ rho {\ frac {\ mathrm {d} \ mathbf {u} _ {\ theta}} {\ mathrm {d} t}} {\ frac {\ mathrm {d} \ theta} {\ mathrm { d} t}}+\ rho \ mathbf {u} _ {\ theta} {\ frac {\ mathrm {d} ^{2} \ theta} {\ mathrm {d} t ^{2}}} \.}$

Ved at erstatte derivaterne af u _ρ og u _θ er accelerationen af ​​partiklen:

${\ displaystyle \ mathbf {a} = {\ frac {\ mathrm {d} ^{2} \ rho} {\ mathrm {d} t ^{2}}} \ mathbf {u} _ {\ rho} +2 {\ frac {\ mathrm {d} \ rho} {\ mathrm {d} t}} \ mathbf {u} _ {\ theta} {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t }}-\ rho \ mathbf {u} _ {\ rho} \ venstre ({\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} \ højre)^{2}+\ rho \ mathbf {u} _ {\ theta} {\ frac {\ mathrm {d} ^{2} \ theta} {\ mathrm {d} t ^{2}}} \,}$

${\ displaystyle = \ mathbf {u} _ {\ rho} \ venstre [{\ frac {\ mathrm {d} ^{2} \ rho} {\ mathrm {d} t ^{2}}}-\ rho \ venstre ({\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} \ højre)^{2} \ højre]+\ mathbf {u} _ {\ theta} \ venstre [2 {\ frac {\ mathrm {d} \ rho} {\ mathrm {d} t}} {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}}+\ rho {\ frac {\ mathrm { d} ^{2} \ theta} {\ mathrm {d} t ^{2}}} \ højre] \}$

${\ displaystyle = \ mathbf {u} _ {\ rho} \ venstre [{\ frac {\ mathrm {d} v _ {\ rho}} {\ mathrm {d} t}}-{\ frac {v _ {\ theta }^{2}} {\ rho}} \ højre]+\ mathbf {u} _ {\ theta} \ venstre [{\ frac {2} {\ rho}} v _ {\ rho} v _ {\ theta}+ \ rho {\ frac {\ mathrm {d}} {\ mathrm {d} t}} {\ frac {v _ {\ theta}} {\ rho}} \ right] \.}$

Som et bestemt eksempel, hvis partiklen bevæger sig i en cirkel med konstant radius R , så d ρ /d t = 0, v = v _θ og:

${\ displaystyle \ mathbf {a} = \ mathbf {u} _ {\ rho} \ venstre [-\ rho \ venstre ({\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} \ \ højre)^{2} \ højre]+\ mathbf {u} _ {\ theta} \ venstre [\ rho {\ frac {\ mathrm {d}^{2} \ theta} {\ mathrm {d} t^{ 2}}} \ højre] \}$

${\ displaystyle = \ mathbf {u} _ {\ rho} \ venstre [-{\ frac {v^{2}} {r}} \ højre]+\ mathbf {u} _ {\ theta} \ venstre [{ \ frac {\ mathrm {d} v} {\ mathrm {d} t}} \ right] \}$

hvor ${\ displaystyle v = v _ {\ theta}.}$

Disse resultater stemmer overens med dem ovenfor for ikke -ensartet cirkulær bevægelse . Se også artiklen om ikke-ensartet cirkulær bevægelse . Hvis denne acceleration ganges med partikelmassen, er det ledende udtryk centripetalkraften, og negativet i det andet udtryk relateret til vinkelacceleration kaldes undertiden Euler -kraften .

For andre baner end cirkulær bevægelse, for eksempel den mere generelle bane, der ses på billedet ovenfor, er det øjeblikkelige rotationscenter og kurvens radius for banen kun indirekte relateret til koordinatsystemet defineret af u _ρ og u _θ og til længde | r ( t ) | = ρ . Derfor er det i det generelle tilfælde ikke ligetil at adskille centripetal- og Euler -udtryk fra ovenstående generelle accelerationsligning. For at håndtere dette problem er lokale koordinater at foretrække, som diskuteret næste gang.

Lokale koordinater

Lokalt koordinatsystem til plan bevægelse på en kurve. To forskellige positioner er vist for afstande s og s + ds langs kurven. På hver position s peger enhedsvektor u _n langs den udadgående normal til kurven, og enhedsvektor u _t er tangential til stien. Kurvens radius af stien er ρ som fundet fra tangentens rotationshastighed til kurven i forhold til buelængde og er radius for den osculerende cirkel i position s . Enhedscirklen til venstre viser enhedsvektorernes rotation med s .

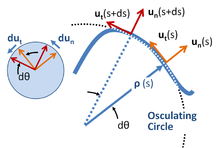
Lokale koordinater betyder et sæt koordinater, der rejser med partiklen og har orientering bestemt af partikelens vej. Enhedsvektorer dannes som vist på billedet til højre, både tangentielt og normalt for stien. Dette koordinatsystem omtales undertiden som indre eller stikkoordinater eller nt-koordinater , for normal-tangential , med henvisning til disse enhedsvektorer. Disse koordinater er et helt specielt eksempel på et mere generelt begreb om lokale koordinater fra teorien om forskellige former.

Afstand langs partiklens vej er buelængden s , der anses for at være en kendt tidsfunktion.

${\ displaystyle s = s (t) \.}$

Et krumningscenter er defineret ved hver position s placeret i en afstand ρ ( krumningsradius ) fra kurven på en linje langs de normale u _n ( s ). Den krævede afstand ρ ( s ) ved buelængde s er defineret i forhold til tangentens rotationshastighed til kurven, som igen bestemmes af selve stien. Hvis tangens orientering i forhold til en eller anden startposition er θ ( s ), er ρ ( s ) defineret af derivatet d θ /d s :

${\ displaystyle {\ frac {1} {\ rho (s)}} = \ kappa (s) = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s}} \.}$

Krumningsradius tages normalt som positiv (det vil sige som en absolut værdi), mens krumningen κ er en signeret størrelse.

En geometrisk tilgang til at finde krumningens centrum og krumningsradius bruger en begrænsende proces, der fører til den osculerende cirkel . Se billedet ovenfor.

Ved hjælp af disse koordinater ses bevægelsen langs stien som en række af cirkulære stier i stadigt skiftende centrum, og på hver position udgør s ikke-ensartet cirkulær bevægelse på den position med radius ρ . Den lokale værdi af vinkelhastigheden er derefter givet ved:

${\ displaystyle \ omega (s) = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s }} {\ frac {\ mathrm {d} s} {\ mathrm {d} t}} = {\ frac {1} {\ rho (s)}} \ {\ frac {\ mathrm {d} s} { \ mathrm {d} t}} = {\ frac {v (s)} {\ rho (s)}} \,}$

med den lokale hastighed v givet af:

${\ displaystyle v (s) = {\ frac {\ mathrm {d} s} {\ mathrm {d} t}} \.}$

Som for de andre eksempler ovenfor, fordi enhedsvektorer ikke kan ændre størrelse, er deres ændringshastighed altid vinkelret på deres retning (se indsatsen til venstre i billedet ovenfor):

${\ displaystyle {\ frac {d \ mathbf {u} _ {\ mathrm {n}} (s)} {ds}} = \ mathbf {u} _ {\ mathrm {t}} (s) {\ frac { d \ theta} {ds}} = \ mathbf {u} _ {\ mathrm {t}} (s) {\ frac {1} {\ rho}} \;}$ ${\ displaystyle {\ frac {d \ mathbf {u} _ {\ mathrm {t}} (s)} {\ mathrm {d} s}} =-\ mathbf {u} _ {\ mathrm {n}} ( s) {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s}} =-\ mathbf {u} _ {\ mathrm {n}} (s) {\ frac {1} {\ rho }} \.}$

Derfor er hastigheden og accelerationen:

${\ displaystyle \ mathbf {v} (t) = v \ mathbf {u} _ {\ mathrm {t}} (s) \;}$

og ved hjælp af differentieringsreglen :

${\ displaystyle \ mathbf {a} (t) = {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {t}} (s)-{ \ frac {v^{2}} {\ rho}} \ mathbf {u} _ {\ mathrm {n}} (s) \;}$ med den tangentielle acceleration ${\ displaystyle {\ frac {\ mathrm {\ mathrm {d}} v} {\ mathrm {\ mathrm {d}} t}} = {\ frac {\ mathrm {d} v} {\ mathrm {d} s }} \ {\ frac {\ mathrm {d} s} {\ mathrm {d} t}} = {\ frac {\ mathrm {d} v} {\ mathrm {d} s}} \ v \.}$

I dette lokale koordinatsystem ligner accelerationen udtrykket for ikke -ensartet cirkulær bevægelse med den lokale radius ρ ( r ), og centripetalaccelerationen identificeres som det andet udtryk.

At udvide denne tilgang til tredimensionelle rumkurver fører til Frenet -Serret -formlerne .

Alternativ tilgang

Når man ser på billedet ovenfor, kan man undre sig over, om der er taget tilstrækkeligt hensyn til forskellen i krumning mellem ρ ( s ) og ρ ( s + d s ) ved beregning af buelængden som d s = ρ ( s ) d θ . Beroligelse på dette punkt kan findes ved hjælp af en mere formel tilgang beskrevet nedenfor. Denne tilgang gør også forbindelse til artiklen om krumning .

For at introducere enhedsvektorerne i det lokale koordinatsystem er en tilgang at begynde med kartesiske koordinater og beskrive de lokale koordinater i form af disse kartesiske koordinater. Med hensyn til buelængde s , lad stien beskrives som:

${\ displaystyle \ mathbf {r} (s) = \ venstre [x (s), \ y (s) \ højre] \.}$

Derefter beskrives en inkrementel forskydning langs stien d s af:

${\ displaystyle \ mathrm {d} \ mathbf {r} (s) = \ left [\ mathrm {d} x (s), \ \ mathrm {d} y (s) \ right] = \ left [x '( s), \ y '(s) \ right] \ mathrm {d} s \,}$

hvor primtal indføres for at betegne derivater med hensyn til s . Størrelsen af ​​denne forskydning er d s , hvilket viser at:

${\ displaystyle \ left [x '(s)^{2}+y' (s)^{2} \ right] = 1 \.}$ (Ligning 1)

Denne forskydning er nødvendigvis en tangent til kurven ved s , hvilket viser, at enhedsvektoren, der tangenter til kurven, er:

${\ displaystyle \ mathbf {u} _ {\ mathrm {t}} (s) = \ left [x '(s), \ y' (s) \ right] \,}$

mens den ydre enhedsvektor normal til kurven er

${\ displaystyle \ mathbf {u} _ {\ mathrm {n}} (s) = \ left [y '(s), \ -x' (s) \ right] \,}$

Orthogonality kan verificeres ved at vise, at vektoren dot produkt er nul. Enhedsstørrelsen af ​​disse vektorer er en konsekvens af ligning. 1 . Ved hjælp af tangentvektoren er vinklen θ for tangenten til kurven givet ved:

${\ displaystyle \ sin \ theta = {\ frac {y '(s)} {\ sqrt {x' (s)^{2}+y '(s)^{2}}}} = y' (s) \;}$ og ${\ displaystyle \ cos \ theta = {\ frac {x '(s)} {\ sqrt {x' (s)^{2}+y '(s)^{2}}}} = x' (s) \.}$

Krumningsradius indføres fuldstændigt formelt (uden behov for geometrisk fortolkning) som:

${\ displaystyle {\ frac {1} {\ rho}} = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s}} \.}$

Afledningen af θ kan findes fra det for synd θ :

${\ displaystyle {\ frac {\ mathrm {d} \ sin \ theta} {\ mathrm {d} s}} = \ cos \ theta {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s }} = {\ frac {1} {\ rho}} \ cos \ theta \ = {\ frac {1} {\ rho}} x '(r) \.}$

Nu:

${\ displaystyle {\ frac {\ mathrm {d} \ sin \ theta} {\ mathrm {d} s}} = {\ frac {\ mathrm {d}} {\ mathrm {d} s}} {\ frac { y '(s)} {\ sqrt {x' (s)^{2}+y '(s)^{2}}}}}$ ${\ displaystyle = {\ frac {y '' (s) x '(s)^{2} -y' (s) x '(s) x' '(s)} {\ left (x' (s)) ^{2}+y '(r)^{2} \ right)^{3/2}}} \,}$

hvor nævneren er enhed. Med denne formel for sinusens derivat bliver krumningsradius:

${\ displaystyle {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} s}} = {\ frac {1} {\ rho}} = y '' (s) x '(s) -y '(s) x' '(s) \}$ ${\ displaystyle = {\ frac {y '' (s)} {x '(s)}} =-{\ frac {x' '(s)} {y' (s)}} \ \}}$

hvor formernes ækvivalens stammer fra differentiering af ligning. 1 :

${\ displaystyle x '(s) x' '(s)+y' (s) y '' (s) = 0 \.}$

Med disse resultater kan accelerationen findes:

${\ displaystyle \ mathbf {a} (s) = {\ frac {\ mathrm {d}} {\ mathrm {d} t}} \ mathbf {v} (s)}$ ${\ displaystyle = {\ frac {\ mathrm {d}} {\ mathrm {d} t}} \ venstre [{\ frac {\ mathrm {d} s} {\ mathrm {d} t}} \ venstre (x '(s), \ y' (s) \ right) \ right] \}$

${\ displaystyle = \ left ({\ frac {\ mathrm {d} ^{2} s} {\ mathrm {d} t ^{2}}} \ right) \ mathbf {u} _ {\ mathrm {t} } (s)+\ venstre ({\ frac {\ mathrm {d} s} {\ mathrm {d} t}} \ right)^{2} \ left (x '' (s), \ y '' ( s) \ højre)}$

${\ displaystyle = \ left ({\ frac {\ mathrm {d} ^{2} s} {\ mathrm {d} t ^{2}}} \ right) \ mathbf {u} _ {\ mathrm {t} } (r)-\ venstre ({\ frac {\ mathrm {d} s} {\ mathrm {d} t}} \ right)^{2} {\ frac {1} {\ rho}} \ mathbf {u } _ {\ mathrm {n}} (r) \,}$

som kan verificeres ved at tage prikproduktet med enhedsvektorerne u _t ( s ) og u _n ( s ). Dette resultat for acceleration er det samme som for cirkulær bevægelse baseret på radius ρ . Ved hjælp af dette koordinatsystem i inertialrammen er det let at identificere den kraft, der er normal på banen som centripetalkraften og den parallelt med banen som tangentialkraften. Fra et kvalitativt synspunkt kan stien tilnærmes en cirkelbue i en begrænset periode, og i den begrænsede tid, en bestemt krumningsradius gælder, kan centrifugalkræfterne og Eulerkræfterne analyseres på basis af cirkulær bevægelse med den radius .

Dette resultat for acceleration stemmer overens med det, der blev fundet tidligere. I denne tilgang håndteres spørgsmålet om ændringen i krumningsradius med s helt formelt, i overensstemmelse med en geometrisk fortolkning, men ikke afhængig af det, og derved undgås eventuelle spørgsmål, som billedet ovenfor kan foreslå om negligering af variationen i ρ .

Eksempel: cirkulær bevægelse

For at illustrere ovenstående formler, lad x , y gives som:

${\ displaystyle x = \ alpha \ cos {\ frac {s} {\ alpha}} \; \ y = \ alpha \ sin {\ frac {s} {\ alpha}} \.}$

Derefter:

${\ displaystyle x^{2}+y^{2} = \ alpha^{2} \,}$

som kan genkendes som en cirkulær vej rundt om oprindelsen med radius α . Positionen s = 0 svarer til [ α , 0] eller klokken 3. For at bruge ovenstående formalisme er derivaterne nødvendige:

${\ displaystyle y^{\ prime} (s) = \ cos {\ frac {s} {\ alpha}} \; \ x^{\ prime} (s) =-\ sin {\ frac {s} {\ alfa}} \,}$

${\ displaystyle y^{\ prime \ prime} (s) =-{\ frac {1} {\ alpha}} \ sin {\ frac {s} {\ alpha}} \; \ x^{\ prime \ prime } (s) =-{\ frac {1} {\ alpha}} \ cos {\ frac {s} {\ alpha}} \.}$

Med disse resultater kan man kontrollere, at:

${\ displaystyle x^{\ prime} (s)^{2}+y^{\ prime} (s)^{2} = 1 \; \ {\ frac {1} {\ rho}} = y^{ \ prime \ prime} (s) x^{\ prime} (s) -y^{\ prime} (s) x^{\ prime \ prime} (s) = {\ frac {1} {\ alpha}} \.}$

Enhedsvektorerne kan også findes:

${\ displaystyle \ mathbf {u} _ {\ mathrm {t}} (s) = \ venstre [-\ sin {\ frac {s} {\ alpha}} \, \ \ cos {\ frac {s} {\ alfa}} \ højre] \; \ \ mathbf {u} _ {\ mathrm {n}} (s) = \ venstre [\ cos {\ frac {s} {\ alpha}} \, \ \ sin {\ frac {s} {\ alpha}} \ right] \,}$

som tjener til at vise, at s = 0 er placeret på position [ ρ , 0] og s = ρ π/2 ved [0, ρ ], hvilket stemmer overens med de originale udtryk for x og y . Med andre ord, s måles mod uret rundt om cirklen fra klokken 3. Desuden kan derivaterne af disse vektorer findes:

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} s}} \ mathbf {u} _ {\ mathrm {t}} (s) =-{\ frac {1} {\ alpha} } \ venstre [\ cos {\ frac {s} {\ alpha}} \, \ \ sin {\ frac {s} {\ alpha}} \ right] =-{\ frac {1} {\ alpha}} \ mathbf {u} _ {\ mathrm {n}} (r) \;}$

${\ displaystyle \ {\ frac {\ mathrm {d}} {\ mathrm {d} s}} \ mathbf {u} _ {\ mathrm {n}} (s) = {\ frac {1} {\ alpha} } \ venstre [-\ sin {\ frac {s} {\ alpha}} \, \ \ cos {\ frac {s} {\ alpha}} \ right] = {\ frac {1} {\ alpha}} \ mathbf {u} _ {\ mathrm {t}} (r) \.}$

For at opnå hastighed og acceleration er en tidsafhængighed for s nødvendig. Til bevægelse mod uret ved variabel hastighed v ( t ):

${\ displaystyle s (t) = \ int _ {0}^{t} \ dt^{\ prime} \ v (t^{\ prime}) \,}$

hvor v ( t ) er hastigheden og t er tiden, og s ( t = 0) = 0. Derefter:

${\ displaystyle \ mathbf {v} = v (t) \ mathbf {u} _ {\ mathrm {t}} (s) \,}$

${\ displaystyle \ mathbf {a} = {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {t}} (s)+v {\ frac {\ mathrm {d}} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {t}} (s) = {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {t}} (s) -v {\ frac {1} {\ alpha}} \ mathbf {u} _ {\ mathrm {n}} (s) {\ frac {\ mathrm {d} s} {\ mathrm {d} t}}}$

${\ displaystyle \ mathbf {a} = {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} \ mathbf {u} _ {\ mathrm {t}} (s)-{\ frac { v^{2}} {\ alpha}} \ mathbf {u} _ {\ mathrm {n}} (r) \,}$

hvor det allerede er fastslået, at α = ρ. Denne acceleration er standardresultatet for ikke-ensartet cirkulær bevægelse .

Se også

Noter og referencer

Yderligere læsning

• Serway, Raymond A .; Jewett, John W. (2004). Fysik for forskere og ingeniører (6. udgave). Brooks/Cole. ISBN 978-0-534-40842-8.
• Tipler, Paul (2004). Fysik for forskere og ingeniører: Mekanik, oscillationer og bølger, termodynamik (5. udgave). WH Freeman. ISBN 978-0-7167-0809-4.
• Centripetal force vs. Centrifugal force , fra en online Regents Exam fysikundervisning af Oswego City School District

eksterne links

• Notater fra University of Winnipeg
• Noter fra fysik og astronomi HyperPhysics ved Georgia State University ; se også hjemmesiden
• Noter fra Britannica
• Noter fra PhysicsNet
• NASA -noter af David P. Stern
• Noter fra U Texas .
• Analyse af smart jojo
• Inuiterne jojo
• Kinematic Models for Design Digital Library (KMODDL)
  Film og fotos af hundredvis af mekaniske systemmodeller ved Cornell University. Indeholder også et e-bogs bibliotek med klassiske tekster om mekanisk design og teknik.