Cirkulær bevægelse - Circular motion

Del af en serie om
Klassisk mekanik
${\displaystyle {\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})}$ Anden lov om bevægelse
Historie Tidslinje Lærebøger
Grene
Grundlæggende
Formuleringer
Kerneemner
Rotation
Forskere
Fysik portal  Kategori
v t e

I fysikken er cirkulær bevægelse en bevægelse af et objekt langs en cirkels omkreds eller rotation langs en cirkulær vej. Det kan være ensartet, med konstant vinkelhastighed og konstant hastighed eller ikke-ensartet med en skiftende rotationshastighed. Den rotati on af et tredimensionalt legeme involverer cirkulær bevægelse af dens dele. Bevægelsesligningerne beskriver bevægelsen af et krops massecenter . I cirkulær bevægelse forbliver afstanden mellem kroppen og et fast punkt på overfladen den samme.

Eksempler på cirkulær bevægelse omfatter: en kunstig satellit, der kredser om jorden i en konstant højde, en loftsventilators blade roterer omkring et nav, en sten, der er bundet til et reb og svinges i cirkler, en bil, der drejer gennem en kurve i en racerbane , en elektron, der bevæger sig vinkelret på et ensartet magnetfelt , og et gear, der drejer inde i en mekanisme.

Da objektets hastighedsvektor konstant ændrer retning, undergår det bevægelige objekt acceleration med en centripetalkraft i retning af rotationscentrum. Uden denne acceleration ville objektet bevæge sig i en lige linje i henhold til Newtons bevægelseslove .

Ensartet cirkulær bevægelse

Figur 1: Hastighed v og acceleration a i ensartet cirkulær bevægelse med vinkelhastighed ω; hastigheden er konstant, men hastigheden er altid tangent til kredsløbet; accelerationen har konstant størrelse, men peger altid mod rotationscentrum.

Figur 2: Hastighedsvektorerne på tidspunktet t og tidspunktet t + dt flyttes fra kredsløbet til venstre til nye positioner, hvor deres haler falder sammen til højre. Fordi hastigheden er fastsat i størrelsesorden ved v = r ω, fejer hastighedsvektorerne også en cirkulær vej med vinkelhastighed ω. Som dt → 0 bliver accelerationsvektoren a vinkelret på v , hvilket betyder, at den peger mod midten af ​​kredsløbet i cirklen til venstre. Vinkel ω dt er den meget lille vinkel mellem de to hastigheder og har en tendens til nul som dt → 0.

Figur 3: (Venstre) Bold i cirkulær bevægelse - reb giver centripetalkraft til at holde bolden i cirkel (højre) Rebet skæres og bolden fortsætter i lige linje med hastighed på tidspunktet for rebskæring i overensstemmelse med Newtons inertilov, fordi centripetalkraft ikke længere er der.

I fysik , jævne cirkelbevægelse beskriver bevægelsen af et legeme gennemkører en cirkulær bane ved konstant hastighed . Da kroppen beskriver cirkulær bevægelse, forbliver dens afstand fra rotationsaksen konstant. Selvom kroppens hastighed er konstant, er dens hastighed ikke konstant: hastighed, en vektormængde , afhænger af både kroppens hastighed og dens kørselsretning. Denne ændrede hastighed indikerer tilstedeværelsen af ​​en acceleration; denne centripetalacceleration er af konstant størrelse og til enhver tid rettet mod rotationsaksen. Denne acceleration produceres til gengæld af en centripetalkraft, som også er konstant i størrelse og rettet mod rotationsaksen.

I tilfælde af rotation omkring en fast akse i et stift legeme , der ikke er ubetydeligt lille i forhold til banens radius, beskriver hver partikel af kroppen en ensartet cirkulær bevægelse med samme vinkelhastighed, men med hastighed og acceleration, der varierer med position i forhold til aksen.

Formler

Figur 1: Vektorforhold til ensartet cirkulær bevægelse; vektor ω, der repræsenterer rotationen, er normal i forhold til kredsløbets plan.

For bevægelse i en cirkel med radius r er cirkelens omkreds C = 2 π r . Hvis perioden for en rotation er T , er vinkelhastigheden, også kendt som vinkelhastighed , ω:

${\displaystyle \omega ={\frac {2\pi }{T}}=2\pi f={\frac {d\theta }{dt}}}$ og enhederne er radianer/sekund

Hastigheden på objektet, der bevæger sig rundt i cirklen, er:

${\displaystyle v={\frac {2\pi r}{T}}=\omega r}$

Vinklen θ fejet ud på en tid t er:

${\displaystyle \theta =2\pi {\frac {t}{T}}=\omega t\,}$

Den vinkelacceleration , α , af partiklen er:

${\displaystyle \alpha ={\frac {d\omega }{dt}}}$

I tilfælde af ensartet cirkulær bevægelse vil α være nul.

Accelerationen på grund af ændring i retningen er:

${\displaystyle a_{c}={\frac {v^{2}}{r}}=\omega ^{2}r}$

Den centripetal og centrifugal kraft kan også findes ved anvendelse acceleration:

${\displaystyle F_{c}={\dot {p}}\ {\overset {{\dot {m}}=0}{=}}\ ma_{c}={\frac {mv^{2}}{r}}}$

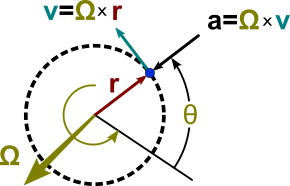
Vektorforholdene er vist i figur 1. Rotationsaksen er vist som en vektor ω vinkelret på kredsløbets plan og med en størrelse ω = d θ / dt . Retningen for ω vælges ved hjælp af højre håndsregel . Med denne konvention til afbildning af rotation er hastigheden givet af et vektorkryds -produkt som

${\displaystyle \mathbf {v} ={\boldsymbol {\omega }}\times \mathbf {r} ,}$

som er en vektor vinkelret på både ω og r ( t ), tangential til banen og af størrelse ω r . På samme måde er accelerationen givet af

${\displaystyle \mathbf {a} ={\boldsymbol {\omega }}\times \mathbf {v} ={\boldsymbol {\omega }}\times \left({\boldsymbol {\omega }}\times \mathbf {r} \right),}$

som er en vektor vinkelret på både ω og v ( t ) af størrelse ω | v | = ω ² r og rettet modsat r ( t ).

I det enkleste tilfælde er hastigheden, massen og radius konstant.

Betragt et legeme på et kilo, der bevæger sig i en cirkel med en radius på en meter, med en vinkelhastighed på en radian i sekundet .

• Den hastighed er 1 meter per sekund.
• Den indadgående acceleration er 1 meter pr. Kvadrat sekund, v ² /r.
• Den udsættes for en centripetalkraft på 1 kilogram meter pr. Kvadrat sekund, hvilket er en newton .
• Den fremdrift af kroppen er 1 kg · m · s ^-1 .
• Den Inertimomentet er 1 kg · m ² .
• Den impulsmoment er 1 kg · m ² · s ^-1 .
• Den kinetiske energi er 1 joule .
• Den omkreds af kredsløb er 2 π (~ 6,283) meter.
• Bevægelsens periode er 2 π sekunder pr. Omgang .
• Den frekvens er (2 π ) ^-1 hertz .

I polære koordinater

Figur 4: Polære koordinater for cirkulær bane. Til venstre er en enhedscirkel, der viser ændringerne og i enhedsvektorerne og for et lille trin i vinkel .${\displaystyle \mathbf {d{\hat {u}}_{R}} }$${\displaystyle \mathbf {d{\hat {u}}_{\theta }} }$${\displaystyle \mathbf {{\hat {u}}_{R}} }$${\displaystyle \mathbf {{\hat {u}}_{\theta }} }$${\displaystyle \mathrm {d\theta } }$${\displaystyle \mathrm {\theta } }$

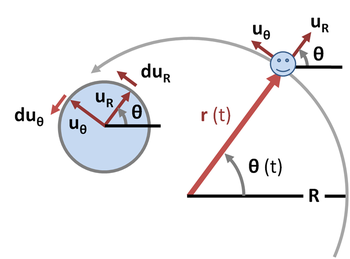
Under cirkulær bevægelse bevæger kroppen sig på en kurve, der kan beskrives i polært koordinatsystem som en fast afstand R fra kredsløbets centrum taget som oprindelse, orienteret i en vinkel θ ( t ) fra en eller anden referenceretning. Se figur 4. Forskydningen vektor er den radiale vektor fra origo til partikel placering: ${\displaystyle {\vec {r}}}$

${\displaystyle {\vec {r}}(t)=R{\hat {u}}_{R}(t)\ ,}$

hvor er enhedsvektoren parallel med radiusvektoren på tidspunktet t og peger væk fra oprindelsen. Det er praktisk også at introducere enhedsvektoren ortogonal til , nemlig . Det er sædvanligt at orientere sig til at pege i kørselsretningen langs banen. ${\displaystyle {\hat {u}}_{R}(t)}$${\displaystyle {\hat {u}}_{R}(t)}$${\displaystyle {\hat {u}}_{\theta }(t)}$${\displaystyle {\hat {u}}_{\theta }(t)}$

Hastigheden er tidsderivatet af forskydningen:

${\displaystyle {\vec {v}}(t)={\frac {d}{dt}}{\vec {r}}(t)={\frac {dR}{dt}}{\hat {u}}_{R}(t)+R{\frac {d{\hat {u}}_{R}}{dt}}\ .}$

Fordi cirkelens radius er konstant, er hastighedens radiale komponent nul. Enhedsvektoren har en tidsvariabel størrelse af enhed, så som tiden varierer, ligger dens spids altid på en cirkel af enhedsradius, med en vinkel θ den samme som vinklen på . Hvis partikelforskydningen roterer gennem en vinkel d θ i tiden dt , gør det også en beskrivelse af en bue på enhedscirklen med størrelse d θ. Se enhedscirklen til venstre i figur 4. Derfor: ${\displaystyle {\hat {u}}_{R}(t)}$${\displaystyle {\vec {r}}(t)}$${\displaystyle {\hat {u}}_{R}(t)}$

${\displaystyle {\frac {d{\hat {u}}_{R}}{dt}}={\frac {d\theta }{dt}}{\hat {u}}_{\theta }(t)\ ,}$

hvor retningen for ændringen skal være vinkelret på (eller med andre ord langs ), fordi enhver ændring i retningen af ville ændre størrelsen på . Tegnet er positivt, fordi en stigning i d θ indebærer objektet og har bevæget sig i retning af . Derfor bliver hastigheden: ${\displaystyle {\hat {u}}_{R}(t)}$${\displaystyle {\hat {u}}_{\theta }(t)}$${\displaystyle d{\hat {u}}_{R}(t)}$${\displaystyle {\hat {u}}_{R}(t)}$${\displaystyle {\hat {u}}_{R}(t)}$${\displaystyle {\hat {u}}_{R}(t)}$${\displaystyle {\hat {u}}_{\theta }(t)}$

${\displaystyle {\vec {v}}(t)={\frac {d}{dt}}{\vec {r}}(t)=R{\frac {d{\hat {u}}_{R}}{dt}}=R{\frac {d\theta }{dt}}{\hat {u}}_{\theta }(t)=R\omega {\hat {u}}_{\theta }(t)\ .}$

Kroppens acceleration kan også opdeles i radiale og tangentielle komponenter. Accelerationen er tidsafledt af hastigheden:

${\displaystyle {\begin{aligned}{\vec {a}}(t)&={\frac {d}{dt}}{\vec {v}}(t)={\frac {d}{dt}}\left(R\omega {\hat {u}}_{\theta }(t)\right)\\&=R\left({\frac {d\omega }{dt}}{\hat {u}}_{\theta }(t)+\omega {\frac {d{\hat {u}}_{\theta }}{dt}}\right)\ .\end{aligned}}}$

Tidsafledningen af findes på samme måde som for . Igen er en enhedsvektor, og dens spids sporer en enhedscirkel med en vinkel, der er π /2 + θ. Dermed en forøgelse af vinkel d θ ved indebærer spor en bue størrelsesorden d θ, og som er ortogonal til , har vi: ${\displaystyle {\hat {u}}_{\theta }(t)}$${\displaystyle {\hat {u}}_{R}(t)}$${\displaystyle {\hat {u}}_{\theta }(t)}$${\displaystyle {\vec {r}}(t)}$${\displaystyle {\hat {u}}_{\theta }(t)}$${\displaystyle {\hat {u}}_{\theta }(t)}$${\displaystyle {\hat {u}}_{R}(t)}$

${\displaystyle {\frac {d{\hat {u}}_{\theta }}{dt}}=-{\frac {d\theta }{dt}}{\hat {u}}_{R}(t)=-\omega {\hat {u}}_{R}(t)\ ,}$

hvor et negativt tegn er nødvendigt at holde ortogonal til . (Ellers vinklen mellem og ville falde med stigning i d . Θ) Se enhedscirklen til venstre i figur 4. Følgelig accelerationen er: ${\displaystyle {\hat {u}}_{\theta }(t)}$${\displaystyle {\hat {u}}_{R}(t)}$${\displaystyle {\hat {u}}_{\theta }(t)}$${\displaystyle {\hat {u}}_{R}(t)}$

${\displaystyle {\begin{aligned}{\vec {a}}(t)&=R\left({\frac {d\omega }{dt}}{\hat {u}}_{\theta }(t)+\omega {\frac {d{\hat {u}}_{\theta }}{dt}}\right)\\&=R{\frac {d\omega }{dt}}{\hat {u}}_{\theta }(t)-\omega ^{2}R{\hat {u}}_{R}(t)\ .\end{aligned}}}$

Den centripetalaccelerationen er den radiale komponent, som er rettet radialt indad:

${\displaystyle {\vec {a}}_{R}(t)=-\omega ^{2}R{\hat {u}}_{R}(t)\ ,}$

mens den tangentielle komponent ændrer hastighedens størrelse :

${\displaystyle {\vec {a}}_{\theta }(t)=R{\frac {d\omega }{dt}}{\hat {u}}_{\theta }(t)={\frac {dR\omega }{dt}}{\hat {u}}_{\theta }(t)={\frac {d\left|{\vec {v}}(t)\right|}{dt}}{\hat {u}}_{\theta }(t)\ .}$

Brug af komplekse tal

Cirkulær bevægelse kan beskrives ved hjælp af komplekse tal . Lad x -aksen være den reelle akse og aksen være den imaginære akse. Kroppens position kan derefter angives som en kompleks "vektor": ${\displaystyle y}$${\displaystyle z}$

${\displaystyle z=x+iy=R(\cos[\theta (t)]+i\sin[\theta (t)])=Re^{i\theta (t)}\ ,}$

hvor i er den imaginære enhed , og er argumentet for det komplekse tal som en funktion af tiden, t . ${\displaystyle \theta (t)}$

Da radius er konstant:

${\displaystyle {\dot {R}}={\ddot {R}}=0\ ,}$

hvor en prik angiver differentiering i forhold til tid.

Med denne notation bliver hastigheden:

${\displaystyle v={\dot {z}}={\frac {d\left(Re^{i\theta [t]}\right)}{dt}}=R{\frac {d\left(e^{i\theta [t]}\right)}{dt}}=Re^{i\theta (t)}{\frac {d(i\theta [t])}{dt}}=iR{\dot {\theta }}(t)e^{i\theta (t)}=i\omega Re^{i\theta (t)}=i\omega z}$

og accelerationen bliver:

${\displaystyle {\begin{aligned}a&={\dot {v}}=i{\dot {\omega }}z+i\omega {\dot {z}}=\left(i{\dot {\omega }}-\omega ^{2}\right)z\\&=\left(i{\dot {\omega }}-\omega ^{2}\right)Re^{i\theta (t)}\\&=-\omega ^{2}Re^{i\theta (t)}+{\dot {\omega }}e^{i{\frac {\pi }{2}}}Re^{i\theta (t)}\ .\end{aligned}}}$

Det første udtryk er modsat i retning af forskydningsvektoren, og det andet er vinkelret på det, ligesom de tidligere resultater vist før.

Hastighed

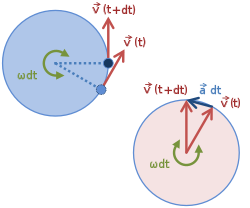
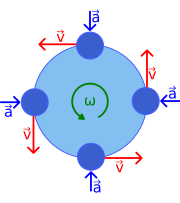
Figur 1 illustrerer hastigheds- og accelerationsvektorer til ensartet bevægelse på fire forskellige punkter i kredsløbet. Fordi hastigheden v er tangent til cirkelbanen, peger der ikke to hastigheder i samme retning. Selvom objektet har en konstant hastighed , ændres dets retning altid. Denne hastighedsændring skyldes en acceleration a , hvis størrelse (ligesom hastighedens) holdes konstant, men hvis retning også altid ændrer sig. De acceleration punkter radialt indad ( centripetalt ) og er vinkelret på hastigheden. Denne acceleration er kendt som centripetal acceleration.

For en sti med radius r , når en vinkel θ fejes ud, er den tilbagelagte afstand på kredsløbets periferi s = r θ. Derfor er rejsehastigheden omkring kredsløbet

${\displaystyle v=r{\frac {d\theta }{dt}}=r\omega ,}$

hvor vinkelhastigheden er ω. (Ved omlægning, ω = v / r .) Således er v en konstant, og hastighedsvektoren v roterer også med konstant størrelse v , med den samme vinkelhastighed ω.

Relativistisk cirkulær bevægelse

I dette tilfælde er tre-accelerationsvektoren vinkelret på trehastighedsvektoren,

${\displaystyle {\vec {u}}\cdot {\vec {a}}=0.}$

og kvadratet med korrekt acceleration, udtrykt som en skalær invariant, det samme i alle referencerammer,

${\displaystyle \alpha ^{2}=\gamma ^{4}a^{2}+\gamma ^{6}({\vec {u}}\cdot {\vec {a}})^{2},}$

bliver udtryk for cirkulær bevægelse,

${\displaystyle \alpha ^{2}=\gamma ^{4}a^{2}.}$

eller ved at tage den positive kvadratrod og bruge tre-accelerationen, når vi frem til den korrekte acceleration for cirkulær bevægelse:

${\displaystyle \alpha =\gamma ^{2}{\frac {v^{2}}{r}}.}$

Acceleration

Den venstre cirkel i figur 2 er kredsløbet, der viser hastighedsvektorerne på to tilstødende tidspunkter. Til højre flyttes disse to hastigheder, så deres haler falder sammen. Fordi hastigheden er konstant, fejer hastighedsvektorerne til højre en cirkel ud, efterhånden som tiden skrider frem. For en fejet vinkel d θ = ω dt er ændringen i v en vektor i vinkel på v og af størrelse v d θ, hvilket igen betyder, at accelerationens størrelse er givet ved

${\displaystyle a_{c}=v{\frac {d\theta }{dt}}=v\omega ={\frac {v^{2}}{r}}}$

Ikke-ensartet

I ikke-ensartet cirkulær bevægelse bevæger et objekt sig i en cirkulær bane med en varierende hastighed . Da hastigheden ændrer sig, er der tangential acceleration ud over normal acceleration.

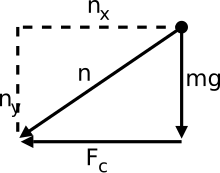
I ikke-ensartet cirkulær bevægelse er netaccelerationen (a) langs Δv-retningen, som er rettet inde i cirklen, men ikke passerer gennem dens centrum (se figur). Nettoaccelerationen kan opdeles i to komponenter: tangential acceleration og normal acceleration også kendt som centripetal eller radial acceleration. I modsætning til tangential acceleration er centripetal acceleration til stede i både ensartet og ikke-ensartet cirkulær bevægelse.

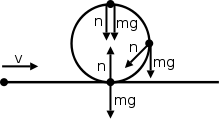
Uensartet cirkelbevægelse, normalkraften ikke altid peger i den modsatte retning af vægt . Her er et eksempel med et objekt, der bevæger sig i en lige sti og derefter sløjfer en sløjfe tilbage i en lige sti igen.

Dette diagram viser den normale kraft, der peger i andre retninger frem for modsat vægtkraften. Den normale kraft er faktisk summen af ​​de radiale og tangentielle kræfter. Komponenten af ​​vægtkraft er ansvarlig for den tangentielle kraft her (Vi har tilsidesat friktionskraft). Radialkraften (centripetalkraft) skyldes ændringen i hastighedsretningen som diskuteret tidligere.

Ved ikke-ensartet cirkulær bevægelse kan normal kraft og vægt pege i samme retning. Begge kræfter kan pege nedad, men alligevel vil objektet forblive i en cirkulær vej uden at falde lige ned. Lad os først se, hvorfor normal kraft i første omgang kan pege nedad. I det første diagram, lad os sige, at objektet er en person, der sidder inde i et plan, de to kræfter peger kun ned, når det når toppen af ​​cirklen. Grunden til dette er, at den normale kraft er summen af ​​den tangentielle kraft og centripetalkraften. Den tangentiale kraft er nul øverst (da der ikke udføres noget arbejde, når bevægelsen er vinkelret på den kraft, der påføres. Her er vægtkraften vinkelret på objektets bevægelsesretning øverst i cirklen) og centripetalkraftpunkter ned, således vil normal kraft også pege ned. Fra et logisk synspunkt vil en person, der rejser i flyet, være på hovedet i toppen af ​​cirklen. I det øjeblik presser personens sæde faktisk ned på personen, hvilket er den normale kraft.

Grunden til, at objektet ikke falder ned, når det kun udsættes for nedadgående kræfter, er en enkel. Tænk på, hvad der holder et objekt oppe, efter at det er kastet. Når et objekt først er kastet i luften, er der kun den nedadgående kraft af jordens tyngdekraft, der virker på objektet. Det betyder ikke, at når et objekt er kastet i luften, vil det falde øjeblikkeligt. Det, der holder objektet oppe i luften, er dets hastighed . Den første af Newtons bevægelseslove siger, at et objekts inerti holder det i bevægelse, og da objektet i luften har en hastighed, vil det have en tendens til at blive ved med at bevæge sig i den retning.

En varierende vinkelhastighed for et objekt, der bevæger sig i en cirkulær bane, kan også opnås, hvis det roterende legeme ikke har en homogen massefordeling. For inhomogene genstande er det nødvendigt at nærme sig problemet som i.

Ansøgninger

At løse applikationer, der beskæftiger sig med ikke-ensartet cirkulær bevægelse, indebærer kraftanalyse. Med ensartet cirkulær bevægelse er den eneste kraft, der virker på et objekt, der bevæger sig i en cirkel, centripetalkraften. I ikke-ensartet cirkulær bevægelse virker der yderligere kræfter på objektet på grund af en tangential acceleration uden nul. Selvom der er yderligere kræfter, der virker på objektet, skal summen af ​​alle de kræfter, der virker på objektet, være lig med centripetalkraften.

${\displaystyle {\begin{aligned}F_{\text{net}}&=ma\\F_{\text{net}}&=ma_{r}\\F_{\text{net}}&={\frac {mv^{2}}{r}}\\F_{\text{net}}&=F_{c}\end{aligned}}}$

Radial acceleration bruges ved beregning af den samlede kraft. Tangential acceleration bruges ikke til at beregne total kraft, fordi den ikke er ansvarlig for at holde objektet i en cirkulær bane. Den eneste acceleration, der er ansvarlig for at holde et objekt i bevægelse i en cirkel, er den radiale acceleration. Da summen af ​​alle kræfter er centripetalkraften, er det ikke nødvendigt at trække centripetalkraft ind i et frit legemsdiagram og anbefales normalt ikke.

Ved hjælp af kan vi tegne frie kropsdiagrammer for at liste alle de kræfter, der virker på et objekt, og derefter sætte det lig med . Bagefter kan vi løse det, der nogensinde er ukendt (dette kan være masse, hastighed, krumningsradius, friktionskoefficient, normal kraft osv.). For eksempel vil det visuelle ovenfor, der viser et objekt øverst i en halvcirkel, blive udtrykt som . ${\displaystyle F_{\text{net}}=F_{c}}$${\displaystyle F_{c}}$${\displaystyle F_{c}=n+mg}$

I ensartet cirkulær bevægelse er den samlede acceleration af et objekt i en cirkulær bane lig med den radiale acceleration. På grund af tilstedeværelsen af ​​tangential acceleration i ikke -ensartet cirkulær bevægelse er det ikke længere sandt. For at finde den totale acceleration af et objekt i ikke -ensartet cirkulær skal du finde vektorsummen af ​​den tangentielle acceleration og den radiale acceleration.

${\displaystyle {\sqrt {a_{r}^{2}+a_{t}^{2}}}=a}$

Radial acceleration er stadig lig med . Tangentialaccelerationen er simpelthen den afledte af hastigheden på et givet punkt: . Denne rodsum af kvadrater med separate radiale og tangentielle accelerationer er kun korrekt for cirkulær bevægelse; for generel bevægelse inden for et plan med polære koordinater , bør Coriolis -udtrykket føjes til , hvorimod radial acceleration derefter bliver . ${\displaystyle {\frac {v^{2}}{r}}}$${\displaystyle a_{t}={\frac {dv}{dt}}}$${\displaystyle (r,\theta )}$${\displaystyle a_{c}=2\left({\frac {dr}{dt}}\right)\left({\frac {d\theta }{dt}}\right)}$${\displaystyle a_{t}}$${\displaystyle a_{r}={\frac {-v^{2}}{r}}+{\frac {d^{2}r}{dt^{2}}}}$

Se også

• Vinklet momentum
• Bevægelsesligninger for cirkulær bevægelse
• Eksempel: cirkulær bevægelse
• Fiktiv kraft
• Geostationær bane
• Geosynkron bane
• Pendul (matematik)
• Reaktiv centrifugalkraft
• Gensidig bevægelse
• Enkel harmonisk bevægelse#Ensartet cirkulær bevægelse
• Slynge (våben)

Referencer

eksterne links

• Physclips: Mekanik med animationer og videoklip fra University of New South Wales
• Circular Motion - et kapitel fra en online lærebog
• Cirkulær bevægelsesforedrag - et videoforedrag om CM
• [1] - en online lærebog med forskellige analyser for cirkulær bevægelse