Bestemmelseskoefficient - Coefficient of determination

Almindelig mindste kvadraters regression af Okuns lov . Da regressionslinjen ikke gå glip af nogen af de punkter, som meget, R ² af regressionen er relativt høj.

Sammenligning af Theil -Sen estimator (sort) og simpel lineær regression (blå) for et sæt punkter med outliers . På grund af de mange outliers, ingen af de regressionslinjer passer godt til dataene, som målt ved den kendsgerning, at hverken giver en meget høj R ² .

I statistik er bestemmelseskoefficienten , også stavet koëfficient , betegnet R ² eller r ² og udtales "R i kvadrat", andelen af ​​variationen i den afhængige variabel, der er forudsigelig ud fra den eller de uafhængige variabler.

Det er en statistik, der bruges i forbindelse med statistiske modeller, hvis hovedformål enten er forudsigelse af fremtidige resultater eller test af hypoteser på grundlag af andre relaterede oplysninger. Det giver et mål for, hvor godt observerede resultater replikeres af modellen, baseret på andelen af ​​den totale variation af resultater forklaret af modellen.

Der er flere definitioner af R ² , der kun undertiden er ækvivalente. En klasse af sådanne tilfælde omfatter den af simpel lineær regression , hvor r ² anvendes i stedet for R ² . Når kun et skæringspunkt er inkluderet, så r ² er simpelthen kvadratet af prøven korrelationskoefficienten (dvs. r ) mellem de observerede resultater og de observerede prædiktor værdier. Hvis yderligere regressorer er inkluderet, R ² er kvadratet på koefficient af multipel korrelation . I begge sådanne tilfælde ligger bestemmelseskoefficienten normalt fra 0 til 1.

Der er tilfælde, hvor den beregningsmæssige definitionen af R ² kan give negative værdier, afhængigt af den definition, der anvendes. Dette kan opstå, når de forudsigelser, der bliver sammenlignet med de tilsvarende resultater, ikke er afledt af en modelpassende procedure ved hjælp af disse data. Selv om der er anvendt en model-fitting procedure, R ² kan stadig være negativ, for eksempel når lineær regression udføres uden at medtage et skæringspunkt, eller når en ikke-lineær funktion anvendes til at tilpasse dataene. I tilfælde, hvor der opstår negative værdier, giver middelværdien af ​​dataene en bedre tilpasning til resultaterne end de tilpassede funktionsværdier i henhold til dette særlige kriterium.

En artikel, der blev offentliggjort i PeerJ Computer Science -tidsskriftet i 2021, siger, at bestemmelseskoefficienten kan være mere sandfærdig end SMAPE , MAE , MAPE , MSE og RMSE i regressionsanalyseevaluering .

Ved evalueringen af goodness-of-fit simuleret ( Y _pred ) vs. målt ( Y _obs ) værdier, er det ikke hensigtsmæssigt at basere dette på R ² for den lineære regression (dvs. Y _obs = m · Y _pred + b ). Den R ² kvantificerer graden af enhver lineær korrelation mellem Y _obs og Y _pred , mens for goodness-of-fit evaluering bør tages kun en specifik lineær korrelation i betragtning: Y _obs = 1 · Y _pred + 0 (dvs. 1: 1 linje).

Definitioner

${\displaystyle R^{2}=1-{\frac {\color {blue}{SS_{\text{res}}}}{\color {red}{SS_{\text{tot}}}}}}$
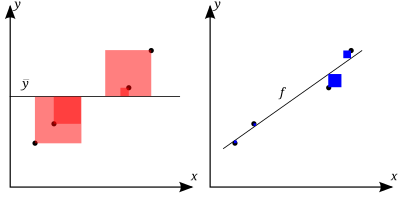
Jo bedre den lineære regression (til højre) passer til dataene i forhold til det simple gennemsnit (på den venstre graf), jo tættere er værdien af 1. Arealerne af de blå firkanter repræsenterer de kvadrerede rester i forhold til den lineære regression. Arealerne af de røde firkanter repræsenterer de kvadrerede rester i forhold til gennemsnitsværdien.${\displaystyle R^{2}}$

Et datasæt har n -værdier mærket y ₁ , ..., y _n (samlet kendt som y _i eller som en vektor y = [ y ₁ , ..., y _n ] ^T ), hver forbundet med en monteret (eller modelleret , eller forudsagt) værdi f ₁ , ..., f _n (kendt som f _i , eller undertiden ŷ _i , som en vektor f ).

Definer resterne som e _i = y _i - f _i (danner en vektor e ).

Hvis er middelværdien af ​​de observerede data: ${\displaystyle {\bar {y}}}$

${\displaystyle {\bar {y}}={\frac {1}{n}}\sum _{i=1}^{n}y_{i}}$

derefter kan datasættets variabilitet måles med to summer af kvadrater formler:

• Summen af ​​kvadrater af rester, også kaldet den resterende sum af firkanter :

${\displaystyle SS_{\text{res}}=\sum _{i}(y_{i}-f_{i})^{2}=\sum _{i}e_{i}^{2}\,}$

• Den samlede sum af firkanter (proportional med variansen af dataene):

${\displaystyle SS_{\text{tot}}=\sum _{i}(y_{i}-{\bar {y}})^{2}}$

Den mest generelle definition af bestemmelseskoefficienten er

${\displaystyle R^{2}=1-{SS_{\rm {res}} \over SS_{\rm {tot}}}\,}$

I bedste tilfælde matcher de modellerede værdier nøjagtigt de observerede værdier, hvilket resulterer i og . En baseline model, som altid forudsiger , vil have . Modeller, der har dårligere forudsigelser end denne baseline, vil have en negativ . ${\displaystyle SS_{\text{res}}=0}$${\displaystyle R^{2}=1}$${\displaystyle {\bar {y}}}$${\displaystyle R^{2}=0}$${\displaystyle R^{2}}$

Forholdet til uforklarlig varians

I generel form, R ² kan ses at være relateret til den del af varians ikke forklares (FVU), idet det andet udtryk sammenligner uforklaret varians (varians af modellens fejl) med den samlede varians (af data):

${\displaystyle R^{2}=1-{\text{FVU}}}$

Som forklaret varians

Antag R ² = 0,49. Dette indebærer, at der er redegjort for 49% af variabiliteten af ​​den afhængige variabel i datasættet, og de resterende 51% af variablen er stadig ikke redegjort for. For regressionsmodeller defineres regressionssummen for kvadrater, også kaldet den forklarede sum af firkanter , som

${\displaystyle SS_{\text{reg}}=\sum _{i}(f_{i}-{\bar {y}})^{2}}$

I nogle tilfælde, som ved simpel lineær regression , er den samlede sum af kvadrater lig med summen af ​​de to andre summer af firkanter defineret ovenfor:

${\displaystyle SS_{\text{res}}+SS_{\text{reg}}=SS_{\text{tot}}}$

Se Partitionering i den generelle OLS -model for en afledning af dette resultat for et tilfælde, hvor forholdet holder. Når dette forhold gør hold, den ovennævnte definition af R ² er ækvivalent med

${\displaystyle R^{2}={\frac {SS_{\text{reg}}}{SS_{\text{tot}}}}={\frac {SS_{\text{reg}}/n}{SS_{\text{tot}}/n}}}$

hvor n er antallet af observationer (tilfælde) på variablerne.

I denne form R ² er udtrykt som forholdet mellem den forklarede varians (varians af modellens forudsigelser, som er SS _reg / n ) til den samlede varians (stikprøvevariansen for den afhængige variable, der er SS _tot / n ).

Denne opdeling af summen af ​​kvadrater gælder for eksempel når modelværdierne ƒ _i er opnået ved lineær regression . En mildere tilstrækkelig tilstand lyder som følger: Modellen har formen

${\displaystyle f_{i}={\widehat {\alpha }}+{\widehat {\beta }}q_{i}\,}$

hvor q _i er vilkårlige værdier, der måske eller måske ikke afhænger af i eller af andre frie parametre (det almindelige valg q _i  =  x _i er kun et specielt tilfælde), og koefficienten estimerer og opnås ved at minimere den resterende sum af kvadrater . ${\displaystyle {\widehat {\alpha }}}$${\displaystyle {\widehat {\beta }}}$

Dette sæt betingelser er vigtigt, og det har en række implikationer for egenskaberne af de monterede rester og de modellerede værdier. Især under disse betingelser:

${\displaystyle {\bar {f}}={\bar {y}}.\,}$

Som kvadratisk korrelationskoefficient

I lineær mindste kvadraters multipel regression med en anslået udtryk for skæringspunktet, R ² er lig med kvadratet på Pearson korrelationskoefficienten mellem de observerede og modellerede (forventede) dataværdier for den afhængige variabel. ${\displaystyle y}$${\displaystyle f}$

I en lineær mindste kvadraters regression med et skæringspunkt og en enkelt forklarer er dette også lig med den kvadrerede Pearson -korrelationskoefficient for den afhængige variabel og forklarende variabel${\displaystyle y}$${\displaystyle x.}$

Det skal ikke forveksles med korrelationskoefficienten mellem to skøn, defineret som

${\displaystyle \rho _{{\widehat {\alpha }},{\widehat {\beta }}}={\operatorname {cov} \left({\widehat {\alpha }},{\widehat {\beta }}\right) \over \sigma _{\widehat {\alpha }}\sigma _{\widehat {\beta }}},}$

hvor kovariansen mellem to koefficientestimater samt deres standardafvigelser er hentet fra covariansmatrixen for koefficientestimaterne.

Under mere generelle modellering forhold, hvor de forudsagte værdier kunne genereres fra en model forskellig fra lineær mindste kvadraters regression, en R ² kan værdien beregnes som kvadratet på korrelationskoefficienten mellem de oprindelige og modellerede dataværdier. I dette tilfælde er værdien ikke direkte et mål for, hvor gode de modellerede værdier er, men derimod et mål for, hvor god en forudsigelse kan konstrueres ud fra de modellerede værdier (ved at oprette en revideret forudsigelse af formen α  +  βƒ _i ). Ifølge Everitt er denne brug specifikt definitionen af ​​udtrykket "koefficient for bestemmelse": kvadratet af korrelationen mellem to (generelle) variabler. ${\displaystyle y}$${\displaystyle f}$

Fortolkning

R ² er en statistik, der vil give nogle oplysninger om godheden i en model. I regression, den R ² determinationskoefficienten er et statistisk mål for hvor godt regression forudsigelser tilnærme de reelle datapunkter. En R ² på 1 angiver, at regression forudsigelser perfekt passer til dataene.

Værdier af R ² uden for området 0 til 1 kan opstå, når modellen passer til data værre end en horisontal hyperplan. Dette ville forekomme, når den forkerte model blev valgt, eller nonsensiske begrænsninger blev anvendt ved en fejl. Hvis ligning 1 af Kvålseth anvendes (dette er den anvendte ligning oftest), R ² kan være mindre end nul. Hvis ligning 2 for Kvålseth bruges, kan R ² være større end én.

I alle tilfælde, hvor R ² er anvendt, er prædiktorer beregnet ved almindelig mindste kvadraters regression: det er, ved at minimere SS _res . I dette tilfælde stiger R ^2, når antallet af variabler i modellen øges ( R ² er monoton stigende med antallet af variabler inkluderet - det vil aldrig falde). Dette illustrerer en ulempe ved en mulig anvendelse af R ² , hvor man kan blive ved med at tilføje variabler ( køkkenvaskregression ) for at øge R ² -værdien. For eksempel, hvis man forsøger at forudsige salget af en bilmodel ud fra bilens gasmængde, pris og motorkraft, kan man inkludere sådanne irrelevante faktorer som det første bogstav i modelnavnet eller højden på den ledende ingeniør, der designer bilen, fordi R ² aldrig vil falde, da variabler tilføjes og sandsynligvis vil opleve en stigning på grund af tilfældighederne alene.

Dette fører til den alternative fremgangsmåde at se på justerede R ² . Forklaringen på denne statistik er næsten det samme som R ² , men det straffer statistikken som ekstra variable er inkluderet i modellen. For andre tilfælde end montering med almindelige mindst kvadrater kan R ² -statistikken beregnes som ovenfor og kan stadig være et nyttigt mål. Hvis montering er af vægtede mindste kvadraters eller generaliserede mindste kvadrater , alternative versioner af R ² kan beregnes i forhold til disse statistiske rammer, mens "rå" R ² stadig kan være nyttig, hvis den er lettere fortolket. Værdier for R ² kan beregnes for enhver form for prædiktiv model, som ikke behøver have et statistisk grundlag.

I en multipel lineær model

Overvej en lineær model med mere end en enkelt forklarende variabel af formen

${\displaystyle Y_{i}=\beta _{0}+\sum _{j=1}^{p}\beta _{j}X_{i,j}+\varepsilon _{i},}$

hvor, for i th tilfælde er svaret variable, er p regressorer, og er en middelværdi nul fejl sigt. Mængderne er ukendte koefficienter, hvis værdier anslås med mindst kvadrater . Bestemmelseskoefficienten R ² er et mål for modellens globale pasform. Specifikt R ² er et element af [0, 1] og repræsenterer andelen af variabilitet i Y _i , der kan tilskrives nogle lineær kombination af regressorer ( forklarende variabler ) i X . ${\displaystyle {Y_{i}}}$${\displaystyle X_{i,1},\dots ,X_{i,p}}$${\displaystyle \varepsilon _{i}}$${\displaystyle \beta _{0},\dots ,\beta _{p}}$

R ² tolkes ofte som andelen af respons variation "forklarede" af regressorer i modellen. Således  angiver R ² = 1, at den tilpassede model forklarer al variabilitet i , mens R ²  = 0 ikke angiver noget 'lineært' forhold (for retlinjeregression betyder det, at modellen med lige linje er en konstant linje (hældning = 0, skæringspunkt) =  ) mellem responsvariablen og regressorer). En indre værdi, såsom R ²  = 0,7 kan fortolkes som følger: "Halvfjerds procent af variansen i responsvariabel kan forklares med de forklarende variable De resterende tredive procent kan tilskrives ukendt, lurer variabler . Eller iboende variabilitet" ${\displaystyle y}$${\displaystyle {\bar {y}}}$

En forsigtighed, der gælder for R ² , som for andre statistiske beskrivelser af korrelation og association, er, at " korrelation ikke indebærer årsagssammenhæng ." Med andre ord, selvom korrelationer undertiden kan give værdifulde spor til afdækning af årsagssammenhænge mellem variabler, er en ikke-nul estimeret korrelation mellem to variabler ikke i sig selv et bevis på, at ændring af værdien af ​​en variabel ville resultere i ændringer i værdierne for andre variabler. For eksempel er praksis med at bære tændstikker (eller en lighter) korreleret med forekomsten af ​​lungekræft, men at bære tændstikker forårsager ikke kræft (i standardbetydningen "årsag").

I tilfælde af en enkelt regressor, monteret af mindste kvadraters, R ² er kvadratet på Pearsons korrelation relatere regressor og svaret variabel. Mere generelt, R ² er kvadratet af korrelationen mellem den beregnede prædiktor og svaret variabel. Med mere end én regressor kan R ² betegnes som koefficienten for multipel bestemmelse .

Inflation af R ²

I mindste kvadraters regression ved anvendelse typiske data, R ² er i det mindste svagt stigende med stigninger i antallet af regressorer i modellen. Fordi stigninger i antallet af regressorer øge værdien af R ² , R ² alene kan ikke anvendes som en meningsfuld sammenligning af modeller med meget forskellige antal uafhængige variable. For en meningsfuld sammenligning mellem to modeller kan der udføres en F-test på den resterende sum af kvadrater , svarende til F-testene i Granger-kausalitet , selvom dette ikke altid er passende. Som en påmindelse om dette, nogle forfattere betegner R ² ved R _q ² , hvor q er antallet af kolonner i X (antallet af explanators herunder konstant).

For at demonstrere denne egenskab skal du først huske på, at målet med mindste kvadraters lineær regression er

${\displaystyle \min _{b}SS_{\text{res}}(b)\Rightarrow \min _{b}\sum _{i}(y_{i}-X_{i}b)^{2}\,}$

hvor X _i er en rækkevektor med værdier af forklarende variabler for tilfælde i og b er en kolonnevektor med koefficienter for de respektive elementer i X _i .

Den optimale værdi af målsætningen er svagt mindre som flere forklarende variable tilsættes, og dermed yderligere søjler af (den forklarende data matrix, hvis jeg th række er X _i ) tilsættes, af, at mindre begrænset minimering fører til en optimal omkostninger, hvilket er svagt mindre end mere begrænset minimering gør. I betragtning af den tidligere konklusion og at bemærke, at kun afhænger y , den ikke-faldende egenskab ved R ² følger direkte fra definitionen ovenfor. ${\displaystyle X}$${\displaystyle SS_{tot}}$

Den intuitive årsag til, at brug af en yderligere forklarende variabel ikke kan sænke R ² er denne: Minimering svarer til at maksimere R ² . Når den ekstra variabel er inkluderet, dataene har altid mulighed for at give det en estimeret koefficient på nul, hvorefter de forudsagte værdier og R ² uændret. Den eneste måde, optimeringsproblemet vil give en koefficient på nul, er, hvis det forbedrer R ² . ${\displaystyle SS_{\text{res}}}$

Advarsler

R ² angiver ikke, om:

• de uafhængige variabler er en årsag til ændringerne i den afhængige variabel ;
• udeladt variabel bias eksisterer;
• den korrekte regression blev brugt;
• det mest passende sæt af uafhængige variabler er valgt;
• der er kollinearitet til stede i dataene om de forklarende variabler;
• modellen kan forbedres ved at bruge transformerede versioner af det eksisterende sæt uafhængige variabler;
• der er nok datapunkter til at drage en solid konklusion.

Udvidelser

Justeret R ²

Anvendelsen af en justeret R ² (én fælles notation , udtales "R bar kvadreret", en anden er eller ) er et forsøg på at redegøre for fænomenet med R ² automatisk og spuriously stigende når ekstra forklarende variabler sættes til modellen. Der er mange forskellige måder at justere på (se en oversigt). Langt den mest anvendte, til det punkt, at den typisk bare kaldes justeret R , er den korrektion, der er foreslået af Mordecai Ezekiel . Den justerede R ² (ifølge Ezekiel) defineres som ${\displaystyle {\bar {R}}^{2}}$${\displaystyle R_{\text{a}}^{2}}$${\displaystyle R_{\text{adj}}^{2}}$

${\displaystyle {\bar {R}}^{2}=1-(1-R^{2}){n-1 \over n-p-1}}$

hvor p er det samlede antal forklarende variabler i modellen (ikke inklusive det konstante udtryk), og n er stikprøvestørrelsen. Det kan også skrives som:

${\displaystyle {\bar {R}}^{2}={1-{SS_{\text{res}}/{\text{df}}_{e} \over SS_{\text{tot}}/{\text{df}}_{t}}}}$

hvor df _t er frihedsgraderne n  - 1 i estimatet af populationsvariansen for den afhængige variabel, og df _e er frihedsgraderne n  -  p  - 1 for estimatet af den underliggende befolkningsfejlvariation.

Den justerede R ² kan være negative, og dens værdi vil altid være mindre end eller lig med den for R ² . Modsætning R ² , de justerede R ² stiger, når stigningen i R ² (som følge af optagelse af en ny forklarende variabel) er mere end man ville forvente at se tilfældigt. Hvis et sæt forklarende variabler med en forudbestemt hierarki af betydning indføres i en regression en ad gangen, med den justeret R ² beregnes hver gang, det niveau, hvor justerede R ² når et maksimum og aftager bagefter, ville være regressionen med den ideelle kombination af at have den bedste pasform uden overskydende/unødvendige vilkår.

Justeret R ² kan fortolkes som en mindre forspændt estimator af befolkningen R ² , mens den observerede prøve R ² er en positivt forspændt estimat af befolkningen værdi. Justeret R ² er mere hensigtsmæssigt, når de evaluerer model fit (variansen i den afhængige variabel, som vedrører de uafhængige variable) og i at sammenligne alternative modeller i funktionen udvælgelse fase af model bygning.

Princippet bag den justerede R ² -statistik kan ses ved at omskrive den almindelige R ² som

${\displaystyle R^{2}={1-{{\textit {VAR}}_{\text{res}} \over {\textit {VAR}}_{\text{tot}}}}}$

hvor og er stikprøvevariationerne for henholdsvis de estimerede restværdier og den afhængige variabel, hvilket kan ses som forudindtaget skøn over populationsvariationerne af fejlene og for den afhængige variabel. Disse skøn erstattes af statistisk upartiske versioner: og . ${\displaystyle {\text{VAR}}_{\text{res}}=SS_{\text{res}}/n}$${\displaystyle {\text{VAR}}_{\text{tot}}=SS_{\text{tot}}/n}$${\displaystyle {\text{VAR}}_{\text{res}}=SS_{\text{res}}/(n-p-1)}$${\displaystyle {\text{VAR}}_{\text{tot}}=SS_{\text{tot}}/(n-1)}$

Trods ved hjælp uvildige estimatorer for befolkningen varianser af fejlen og den afhængige variabel, justeret R ² er ikke en estimator af befolkningen R ² , hvilke resultater ved at bruge befolkningen varianser af de fejl og den afhængige variabel i stedet for at estimere dem. Ingram Olkin og John W. Pratt udledte den minimal-varians upartiske estimator for befolkningen R ² , som er kendt som Olkin-Pratt estimator. Sammenligninger af forskellige tilgange til justering R ² konkluderes, at i de fleste situationer enten en omtrentlig version af Olkin-Pratt estimator eller den nøjagtige Olkin-Pratt estimator bør foretrækkes frem (Ez) tilpasset R ² .

Delbestemmelseskoefficient

Delbestemmelseskoefficienten kan defineres som andelen af ​​variation, der ikke kan forklares i en reduceret model, men kan forklares med de forudsigere, der er angivet i en fuld (er) model. Denne koefficient bruges til at give indsigt i, om en eller flere yderligere forudsigere kan være nyttige i en mere fuldstændigt specificeret regressionsmodel.

Beregningen for den delvise R ² er relativt ligetil efter estimering af to modeller og generering af ANOVA -tabeller for dem. Beregningen for den delvise R ² er

${\displaystyle {\frac {SS_{\text{ res, reduced}}-SS_{\text{ res, full}}}{SS_{\text{ res, reduced}}}},}$

som er analog med den sædvanlige bestemmelseskoefficient:

${\displaystyle {\frac {SS_{\text{tot}}-SS_{\text{res}}}{SS_{\text{tot}}}}.}$

Generalisering og nedbrydning af R ²

Som forklaret ovenfor undersøger modelvalg heuristikker som det justerede kriterium og F-testen, om totalen stiger tilstrækkeligt til at afgøre, om en ny regressor skal føjes til modellen. Hvis der tilføjes en regressor til modellen, der er stærkt korreleret med andre regressorer, der allerede er inkluderet, så stiger totalet næppe, selvom den nye regressor er relevant. Som et resultat vil ovennævnte heuristik ignorere relevante regressorer, når krydskorrelationer er høje. ${\displaystyle R^{2}}$${\displaystyle R^{2}}$${\displaystyle R^{2}}$

Geometrisk fremstilling af .${\displaystyle r^{2}}$

Alternativt kan man dekomponere en generaliseret version af for at kvantificere relevansen af ​​at afvige fra en hypotese. Som Hoornweg (2018) viser, flere svind estimatorer - såsom Bayesian lineære regression , ridge regression , og (adaptive) lasso - gøre brug af denne nedbrydning af når de gradvist skrumpe parametre fra ubegrænset OLS løsninger i retning af hypotetiske værdier. Lad os først definere den lineære regressionsmodel som ${\displaystyle R^{2}}$${\displaystyle R^{2}}$

${\displaystyle y=X\beta +\varepsilon .}$

Det antages, at matrixen er standardiseret med Z-score, og at søjlevektoren er centreret til at have et middelværdi på nul. Lad søjlevektoren referere til de hypotetiserede regressionsparametre og lad kolonnevektoren angive de estimerede parametre. Vi kan derefter definere ${\displaystyle X}$${\displaystyle y}$${\displaystyle \beta _{0}}$${\displaystyle b}$

${\displaystyle R^{2}=1-{\frac {(y-Xb)'(y-Xb)}{(y-X\beta _{0})'(y-X\beta _{0})}}.}$

Et på 75% betyder, at nøjagtigheden i prøven forbedres med 75%, hvis de dataoptimerede løsninger bruges i stedet for de hypotetiserede værdier. I det særlige tilfælde, der er en vektor af nuller, får vi det traditionelle igen. ${\displaystyle R^{2}}$${\displaystyle b}$${\displaystyle \beta _{0}}$${\displaystyle \beta _{0}}$${\displaystyle R^{2}}$

Den individuelle effekt på at afvige fra en hypotese kan beregnes med ('R-ydre'). Denne gange matrix er givet ved ${\displaystyle R^{2}}$${\displaystyle R^{\otimes }}$${\displaystyle p}$${\displaystyle p}$

${\displaystyle R^{\otimes }=(X'{\tilde {y}}_{0})(X'{\tilde {y}}_{0})'(X'X)^{-1}({\tilde {y}}_{0}'{\tilde {y}}_{0})^{-1},}$

hvor . De diagonale elementer i præcist tilføjer op til . Hvis regressorer er ukorrelerede og er en vektor af nuller, svarer det diagonale element simpelthen til værdien mellem og . Når regressorer og er korreleret, kan stige på bekostning af et fald i . Som følge heraf kan de diagonale elementer af være mindre end 0 og i mere undtagelsestilfælde større end 1. For at håndtere sådanne usikkerheder tager flere krympestimatører implicit et vægtet gennemsnit af de diagonale elementer for at kvantificere relevansen af ​​at afvige fra en hypotetiseret værdi. Klik på lassoen for et eksempel. ${\displaystyle {\tilde {y}}_{0}=y-X\beta _{0}}$${\displaystyle R^{\otimes }}$${\displaystyle R^{2}}$${\displaystyle \beta _{0}}$${\displaystyle j^{\text{th}}}$${\displaystyle R^{\otimes }}$${\displaystyle r^{2}}$${\displaystyle x_{j}}$${\displaystyle y}$${\displaystyle x_{i}}$${\displaystyle x_{j}}$${\displaystyle R_{ii}^{\otimes }}$${\displaystyle R_{jj}^{\otimes }}$${\displaystyle R^{\otimes }}$${\displaystyle R^{\otimes }}$

R ² i logistisk regression

I tilfælde af logistisk regression , der normalt passer med maksimal sandsynlighed , er der flere valg af pseudo-R ² .

Den ene er den generaliserede R ² oprindeligt foreslået af Cox & Snell, og uafhængigt af Magee:

${\displaystyle R^{2}=1-\left({{\mathcal {L}}(0) \over {\mathcal {L}}({\widehat {\theta }})}\right)^{2/n}}$

hvor er sandsynligheden for modellen med kun skæringspunktet, er sandsynligheden for den estimerede model (dvs. modellen med et givet sæt parameterestimater) og n er stikprøvestørrelsen. Det omskrives let til: ${\displaystyle {\mathcal {L}}(0)}$${\displaystyle {{\mathcal {L}}({\widehat {\theta }})}}$

${\displaystyle R^{2}=1-e^{{\frac {2}{n}}(\ln({\mathcal {L}}(0))-\ln({\mathcal {L}}({\widehat {\theta }}))}=1-e^{-D/n}}$

hvor D er teststatistikken for sandsynlighedsforholdstesten .

Nagelkerke bemærkede, at det havde følgende egenskaber:

1. Det er i overensstemmelse med den klassiske bestemmelseskoefficient, når begge kan beregnes;
2. Dens værdi maksimeres ved den maksimale sandsynlighedsestimering af en model;
3. Det er asymptotisk uafhængigt af prøvestørrelsen;
4. Fortolkningen er andelen af ​​variationen forklaret af modellen;
5. Værdierne er mellem 0 og 1, hvor 0 angiver, at modellen ikke forklarer nogen variation, og 1 angiver, at den perfekt forklarer den observerede variation;
6. Det har ikke nogen enhed.

Men i tilfælde af en logistisk model, hvor kan ikke være større end 1, R ² er mellem 0 og : således, Nagelkerke foreslået muligheden for at definere en skaleret R ² som R ² / R ² _max . ${\displaystyle {\mathcal {L}}({\widehat {\theta }})}$${\displaystyle R_{\max }^{2}=1-({\mathcal {L}}(0))^{2/n}}$

Sammenligning med norm for restprodukter

Lejlighedsvis bruges normen for restprodukter til at indikere god pasform. Dette udtryk beregnes som kvadratroden af summen af ​​kvadrater af rester :

${\displaystyle {\text{norm of residuals}}={\sqrt {SS_{\text{res}}}}=\|e\|.}$

Både R ² og normen af restprodukter har deres relative fordele. For mindste kvadraters analyse R ² varierer mellem 0 og 1, med større tal, der angiver bedre passer og 1 repræsenterer en perfekt pasform. Normen for rester varierer fra 0 til uendeligt med mindre tal, der angiver bedre pasninger og nul angiver en perfekt pasform. En fordel og ulempe ved R ² er udtrykket virker til at normalisere værdien. Hvis y _I værdier er alle multipliceret med en konstant, vil normen af restprodukter også ændre ved, at konstant, men R ² vil forblive den samme. Som et grundlæggende eksempel passer de lineære mindste firkanter til datasættet: ${\displaystyle SS_{\text{tot}}}$

${\displaystyle {\begin{array}{rcrrrrr}x&=&1,&2,&3,&4,&5\\y&=&1.9,&3.7,&5.8,&8.0,&9.6\end{array}}}$

R ² = 0,998, og norm af restprodukter = 0,302. Hvis alle værdier af y multipliceres med 1000 (for eksempel i en SI-præfiks ændre), derefter R ² forbliver den samme, men norm af restprodukter = 302.

En anden enkeltparameterindikator for tilpasning er RMSE for resterne eller standardafvigelse for resterne. Dette ville have en værdi på 0,135 for ovenstående eksempel, da tilpasningen var lineær med et uforceret skæringspunkt.

Historie

Oprettelsen af ​​bestemmelseskoefficienten er blevet tilskrevet genetikeren Sewall Wright og blev første gang offentliggjort i 1921.

Se også

• Anscombes kvartet
• Variansfraktion uforklarlig
• Pasformens godhed
• Nash – Sutcliffe model effektivitetskoefficient ( hydrologiske anvendelser )
• Pearson produkt-moment korrelationskoefficient
• Proportionelt fald i tab
• Validering af regressionsmodel
• Rod betyder kvadratisk afvigelse
• Trinvis regression
• t -test af${\displaystyle H_{0}\colon R^{2}=0.}$

Noter

Yderligere læsning

• Gujarati, Damodar N .; Porter, Dawn C. (2009). Grundlæggende økonometri (femte udgave). New York: McGraw-Hill/Irwin. s. 73–78. ISBN 978-0-07-337577-9.
• Hughes, Ann; Grawoig, Dennis (1971). Statistik: Et fundament for analyse . Læsning: Addison-Wesley. s.  344–348 . ISBN 0-201-03021-7.
• Kmenta, Jan (1986). Elements of Econometrics (anden udgave). New York: Macmillan. s.  240–243 . ISBN 978-0-02-365070-3.
• Lewis-Beck, Michael S .; Skalaban, Andrew (1990). "The R -Squared: Some Straight Talk". Politisk analyse . 2 : 153–171. doi : 10.1093/pan/2.1.153 . JSTOR  23317769 .
• Chicco, Davide; Warrens, Matthijs J .; Jurman, Giuseppe (2021). "Bestemmelseskoefficienten R-kvadrat er mere informativ end SMAPE, MAE, MAPE, MSE og RMSE i evaluering af regressionsanalyse" . PeerJ datalogi . 7 (e623): 1–24. doi : 10.7717/peerj-cs.623 .