Femdimensionalt rum - Five-dimensional space
Et femdimensionelt rum er et rum med fem dimensioner . I matematik kan en sekvens af N -tal repræsentere en placering i et N -dimensionelt rum . Hvis fortolket fysisk, som er en mere end de sædvanlige tre rumlige dimensioner og den fjerde dimension af tid brugt i relativistisk fysik . Om universet er femdimensionalt eller ej, er et debatemne.
Fysik
Meget af det tidlige arbejde med femdimensionelt rum var i et forsøg på at udvikle en teori, der forener de fire grundlæggende vekselvirkninger i naturen: stærke og svage atomkræfter, tyngdekraft og elektromagnetisme . Den tyske matematiker Theodor Kaluza og den svenske fysiker Oskar Klein udviklede uafhængigt af Kaluza -Klein -teorien i 1921, som brugte den femte dimension til at forene tyngdekraften med elektromagnetisk kraft . Selvom deres tilgange senere blev fundet at være i det mindste delvist unøjagtige, dannede konceptet et grundlag for yderligere forskning i løbet af det sidste århundrede.
For at forklare, hvorfor denne dimension ikke ville være direkte observerbar, foreslog Klein, at den femte dimension ville blive rullet op i en lille, kompakt sløjfe i størrelsesordenen 10 -33 centimeter. Under sin begrundelse forestillede han sig lyset som en forstyrrelse forårsaget af rislende i den højere dimension lige uden for menneskets opfattelse, svarende til hvordan fisk i en dam kun kan se skygger af krusninger over vandoverfladen forårsaget af regndråber. Selvom det ikke kan påvises, ville det indirekte indebære en forbindelse mellem tilsyneladende ikke -relaterede kræfter. Kaluza -Klein -teorien oplevede en genoplivning i 1970'erne på grund af fremkomsten af superstrengteori og supergravitation : konceptet om, at virkeligheden består af vibrerende energistrenge, et postulat, der kun er matematisk levedygtigt i ti dimensioner eller mere. Superstringteori udviklede sig derefter til en mere generaliseret tilgang kendt som M-teori . M-teori foreslog en potentielt observerbar ekstra dimension ud over de ti væsentlige dimensioner, der ville muliggøre eksistensen af superstrenge. De øvrige 10 dimensioner komprimeres eller "rulles op" til en størrelse under det subatomære niveau. Kaluza – Klein -teorien i dag ses i det væsentlige som en målingsteori , hvor måleren er cirkelgruppen .
Den femte dimension er vanskelig at observere direkte, selvom Large Hadron Collider giver mulighed for at registrere indirekte bevis på dens eksistens. Fysikere teoretiserer, at kollisioner af subatomære partikler igen producerer nye partikler som følge af kollisionen, herunder en graviton, der undslipper fra den fjerde dimension, eller klid , der lækker ud i en femdimensionel bulk. M-teori ville forklare tyngdekraftens svaghed i forhold til de andre grundlæggende naturkræfter, som det for eksempel kan ses, når man bruger en magnet til at løfte en nål fra et bord-magneten er i stand til at overvinde hele tyngdekraften jorden med lethed.
Matematiske tilgange blev udviklet i begyndelsen af det 20. århundrede, der betragtede den femte dimension som en teoretisk konstruktion. Disse teorier henviser til Hilbert -rummet , et begreb, der postulerer et uendeligt antal matematiske dimensioner for at give mulighed for et ubegrænset antal kvantetilstande. Einstein , Bergmann og Bargmann senere forsøgt at udvide de fire-dimensional rumtid af generelle relativitetsteori i en ekstra fysisk dimension til at indarbejde elektromagnetisme, selvom de var forgæves. I deres papir fra 1938 var Einstein og Bergmann blandt de første til at introducere det moderne synspunkt om, at en firdimensionel teori, der falder sammen med Einstein-Maxwell-teorien på lange afstande, stammer fra en femdimensionel teori med fuldstændig symmetri i alle fem dimensioner . De foreslog, at elektromagnetisme skyldes et gravitationsfelt, der er "polariseret" i den femte dimension.
Den største nyhed hos Einstein og Bergmann var seriøst at betragte den femte dimension som en fysisk enhed, snarere end en undskyldning for at kombinere den metriske tensor og det elektromagnetiske potentiale. Men de afviste derefter og ændrede teorien til at bryde dens femdimensionale symmetri. Deres ræsonnement, som foreslået af Edward Witten , var, at den mere symmetriske version af teorien forudsagde eksistensen af et nyt langdistancefelt, et som var både masseløst og skalært , hvilket ville have krævet en grundlæggende ændring af Einsteins generelle relativitetsteori . Minkowski-rummet og Maxwells ligninger i vakuum kan indlejres i en femdimensionel Riemann-krumningstensor .
I 1993 fremsatte fysikeren Gerard 't Hooft det holografiske princip , der forklarer, at informationen om en ekstra dimension er synlig som en krumning i en rumtid med en færre dimension . For eksempel er hologrammer tredimensionelle billeder placeret på en todimensionel overflade, hvilket giver billedet en krumning, når observatøren bevæger sig. På samme måde manifesterer den fjerde dimension sig i generel relativitet i observerbare tre dimensioner som krumningsbanen for en bevægelig uendelig (test) partikel. 'T Hooft har spekuleret i, at den femte dimension virkelig er rumtiden stof .
Femdimensionel geometri
Ifølge Kleins definition, "er en geometri undersøgelsen af de rumvarende egenskaber i en rumtid under transformationer i sig selv." Derfor studerer geometrien i 5. dimension de invariante egenskaber ved sådan rumtid, når vi bevæger os inden for den, udtrykt i formelle ligninger.
Polytoper
I fem eller flere dimensioner findes der kun tre almindelige polytoper . I fem dimensioner er de:
- Den 5-simplex af simplex familie, {3,3,3,3}, med 6 knudepunkter, 15 kanter, 20 flader (hver en ligesidet trekant ), 15-celler (hver en regelmæssig tetraeder ) og 6 hypercells (hver en 5-celle ).
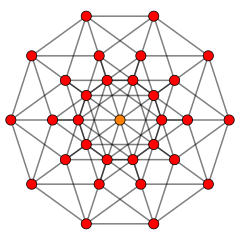
- Den 5-terning af hyperkube familien, {4,3,3,3}, med 32 vertices, 80 kanter, 80 flader (hver en firkant ), 40-celler (hver en terning ), og 10 hypercells (hver en Tesseract ) .
- Den 5-orthoplex af indlægget polytop familien, {3,3,3,4}, med 10 vertices, 40 kanter, 80 flader (hver en trekant ), 80-celler (hver en tetraeder ), og 32 hypercells (hver en 5 -celle ).
En vigtig ensartet 5-polytop er 5-demicube , h {4,3,3,3} har halvdelen af 5-terningens (16) hjørner, afgrænset af vekslende 5-cellers og 16-cellede hyperceller. Den udvidede eller sterikerede 5-simplex er toppunktsfiguren af A 5- gitteret ,
. Det og har en fordoblet symmetri fra dets symmetriske Coxeter -diagram. Gitterets kyssetal, 30, er repræsenteret i dets hjørner. Den udbedrede 5-ortoplex er toppunktfiguren af D 5- gitteret ,
. Dens 40 hjørner repræsenterer kyssetallet på gitteret og det højeste for dimension 5.
| A 5 | Aut (A 5 ) | B 5 | D 5 | ||
|---|---|---|---|---|---|
 5-simplex {3,3,3,3} |
 Sterikeret 5-simplex
|
5-terning  {4,3,3,3} |
 5-ortoplex {3,3,3,4} |
 Udbedret 5-ortoplex r {3,3,3,4} |
 5-demicube  h {4,3,3,3} |
Hypersfære
En hypersfære i 5-rum (også kaldet en 4-kugle på grund af dens overflade er 4-dimensionel) består af sættet af alle punkter i 5-rum i en fast afstand r fra et centralt punkt P. Hypervolumen, der er omsluttet af denne overflade er:
Se også
Referencer
Yderligere læsning
- Wesson, Paul S. (1999). Space-Time-Matter, Modern Kaluza-Klein Theory . Singapore: World Scientific. ISBN 981-02-3588-7.
- Wesson, Paul S. (2006). Femdimensionel fysik: Klassiske og kvante konsekvenser af Kaluza-Klein Cosmology . Singapore: World Scientific. ISBN 981-256-661-9.
- Weyl, Hermann , Raum, Zeit, Materie , 1918. 5 udg. til 1922 udg. med noter af Jūrgen Ehlers, 1980. trans. 4. udgave. Henry Brose, 1922 Space Time Matter , Methuen, rept. 1952 Dover. ISBN 0-486-60267-2 .