Gruppering - Group ring

I algebra er en gruppering et gratis modul og samtidig en ring , der er konstrueret på en naturlig måde ud fra en given ring og en given gruppe . Som et gratis modul er dens ring af skalarer den givne ring, og dens grundlag er en række elementer i den givne gruppe. Som en ring er dens tilføjelseslov den for det frie modul, og dens multiplikation strækker sig "ved lineæritet" til den givne gruppelov på grundlag. Mindre formelt er en gruppering en generalisering af en given gruppe ved at vedhæfte hvert element i gruppen en "vægtningsfaktor" fra en given ring.

Hvis ringen er kommutativ, betegnes gruppering også som en gruppealgebra , for den er faktisk en algebra over den givne ring. En gruppealgebra over et felt har en yderligere struktur af en Hopf -algebra ; i dette tilfælde kaldes det således en gruppe Hopf -algebra .

Grupperingsapparatet er især nyttigt i teorien om gruppeforestillinger .

Definition

Lad G være en gruppe, skrevet multiplicativt, og lad R være en ring. Gruppering af G over R , som vi vil betegne med R [ G ] (eller simpelthen RG ), er sættet med kortlægninger f  : G → R med begrænset støtte (f (g) er nul for kun begrænset mange elementer g) , hvor modulets skalarprodukt αf af en skalar α i R og en kortlægning f er defineret som kortlægningen , og modulgruppesummen for to kortlægninger f og g er defineret som kortlægningen . For at gøre additivgruppen R [ G ] til en ring definerer vi produktet af f og g som kortlægning ${\ displaystyle x \ mapsto \ alpha \ cdot f (x)}$${\ displaystyle x \ mapsto f (x)+g (x)}$

${\ displaystyle x \ mapsto \ sum _ {uv = x} f (u) g (v) = \ sum _ {u \ i G} f (u) g (u^{-1} x).}$

Summationen er legitim, fordi f og g er af endelig støtte, og ringaksiomerne let kan verificeres.

Nogle variationer i notation og terminologi er i brug. Især er kortlægningerne som f  : G → R undertiden skrevet som det, der kaldes "formelle lineære kombinationer af elementer af G , med koefficienter i R ":

${\ displaystyle \ sum _ {g \ i G} f (g) g,}$

eller simpelthen

${\ displaystyle \ sum _ {g \ i G} f_ {g} g,}$

hvor dette ikke skaber forvirring.

Bemærk, at hvis ringen R er i virkeligheden et felt K , hvorefter modulet struktur af gruppen ring RG er i virkeligheden en vektorrum over K .

Eksempler

1. Lad G = C ₃ , den cykliske gruppe af orden 3, med generator og identitet element 1 _G . Et element r af C [ G ] kan skrives som ${\ displaystyle a}$

${\ displaystyle r = z_ {0} 1_ {G}+z_ {1} a+z_ {2} a^{2} \,}$

hvor z ₀ , z ₁ og z ₂ er i C , de komplekse tal . Dette er det samme som et polynomium ring i variabel , således at det vil sige C [ G ] er isomorf til ringen C [ ] / . ${\ displaystyle a}$${\ displaystyle a^{3} = a^{0} = 1}$${\ displaystyle a}$${\ displaystyle (a^{3} -1)}$

Skriver et andet element s som deres sum er ${\ displaystyle s = w_ {0} 1_ {G}+w_ {1} a+w_ {2} a^{2}}$

${\ displaystyle r+s = (z_ {0}+w_ {0}) 1_ {G}+(z_ {1}+w_ {1}) a+(z_ {2}+w_ {2}) a^{2 } \,}$

og deres produkt er

${\ displaystyle rs = (z_ {0} w_ {0}+z_ {1} w_ {2}+z_ {2} w_ {1}) 1_ {G}+(z_ {0} w_ {1}+z_ { 1} w_ {0}+z_ {2} w_ {2}) a+(z_ {0} w_ {2}+z_ {2} w_ {0}+z_ {1} w_ {1}) a^{2} .}$

Bemærk, at identitetselementet 1 _G i G inducerer en kanonisk indlejring af koefficientringen (i dette tilfælde C ) i C [ G ]; imidlertid strengt taget den multiplikative identitet element i C [ G ] er 1⋅1 _G , hvor den første 1 kommer fra C , og den anden fra G . Det additive identitetselement er nul.

Når G er en ikke-kommutativ gruppe, skal man være omhyggelig med at bevare rækkefølge for gruppeelementerne (og ikke ved et uheld pendle dem), når man multiplicerer vilkårene.

2. Et andet eksempel er, at de Laurent polynomier over en ring R : disse er intet mere eller mindre end den gruppe ring i uendelige cykliske gruppe Z i R .

3. Lad Q være kvaterniongruppen med elementer . Overvej gruppering R Q , hvor R er mængden af ​​reelle tal. Et vilkårligt element i denne gruppering er af formen ${\ displaystyle \ {e, {\ bar {e}}, i, {\ bar {i}}, j, {\ bar {j}}, k, {\ bar {k}} \}}$

${\ displaystyle x_ {1} \ cdot e+x_ {2} \ cdot {\ bar {e}}+x_ {3} \ cdot i+x_ {4} \ cdot {\ bar {i}}+x_ {5 } \ cdot j+x_ {6} \ cdot {\ bar {j}}+x_ {7} \ cdot k+x_ {8} \ cdot {\ bar {k}}}$

hvor er et reelt tal. ${\ displaystyle x_ {i}}$

Multiplikation, som i enhver anden gruppering, defineres baseret på gruppeoperationen. For eksempel,

${\ displaystyle {\ begin {align} {\ big (} 3 \ cdot e+{\ sqrt {2}} \ cdot i {\ big)} {\ big (} {\ frac {1} {2}} \ cdot {\ bar {j}} {\ big)} & = (3 \ cdot e) ({\ frac {1} {2}} \ cdot {\ bar {j}})+({\ sqrt {2}} \ cdot i) ({\ frac {1} {2}} \ cdot {\ bar {j}}) \\ & = {\ frac {3} {2}} \ cdot {\ big (} (e) ( {\ bar {j}}) {\ big)}+{\ frac {\ sqrt {2}} {2}} \ cdot {\ big (} (i) ({\ bar {j}}) {\ big )} \\ & = {\ frac {3} {2}} \ cdot {\ bar {j}}+{\ frac {\ sqrt {2}} {2}} \ cdot k \ end {justeret}}. }$

Bemærk, at R Q er ikke det samme som skew området quaternions flere end R . Dette skyldes skew området quaternions opfylder yderligere forbindelser i ringen, såsom , hvorimod i gruppen ringen R Q , er ikke lig med . For at være mere specifik har gruppering R Q dimension 8 som et reelt vektorrum , mens skævfeltet i kvartærer har dimension 4 som et reelt vektorrum . ${\ displaystyle -1 \ cdot i = -i}$${\ displaystyle -1 \ cdot i}$${\ displaystyle 1 \ cdot {\ bar {i}}}$

4. Et andet eksempel på en ikke-abelsk gruppering er, hvor er den symmetriske gruppe på 3 bogstaver. Dette er ikke et integreret domæne, da vi har, hvor elementet er en transposition-en permutation, der kun bytter 1 og 2. Derfor behøver gruppering ikke at være et integreret domæne, selv når den underliggende ring er et integreret domæne. ${\ displaystyle \ mathbb {Z} [\ mathbb {S} _ {3}]}$${\ displaystyle \ mathbb {S} _ {3}}$${\ displaystyle [1- (12)]*[1+ (12)] = 1- (12)+(12)-(12) (12) = 1-1 = 0}$${\ displaystyle (12) \ in \ mathbb {S} _ {3}}$

Nogle grundlæggende egenskaber

Anvendelse af 1 til at betegne det multiplikative identitet af ringen R , og betegner gruppen enheden ved 1 _G , ringen R [ G ] indeholder en delring isomorf til R , og dens gruppe af invertible elementer indeholder en undergruppe isomorf til G . For at overveje indikatorfunktionen for {1 _G }, som er vektoren f defineret af

${\ displaystyle f (g) = 1 \ cdot 1_ {G}+\ sum _ {g \ not = 1_ {G}} 0 \ cdot g = \ mathbf {1} _ {\ {1_ {G} \}} (g) = {\ begin {cases} 1 & g = 1_ {G} \\ 0 & g \ neq 1_ {G} \ end {cases}},}$

mængden af alle skalære multipla af f er en delring af R [ G ] isomorf til R . Og hvis vi kortlægger hvert element s i G til indikatorfunktionen for { s }, som er vektoren f defineret af

${\ displaystyle f (g) = 1 \ cdot s+\ sum _ {g \ not = s} 0 \ cdot g = \ mathbf {1} _ {\ {s \}} (g) = {\ begin {cases} 1 & g = s \\ 0 & g \ neq s \ end {cases}}}$

den resulterende kortlægning er en injektiv gruppehomomorfisme (med hensyn til multiplikation, ikke addition, i R [ G ]).

Hvis R og G begge er kommutative (dvs. R er kommutative og G er en abelsk gruppe ), er R [ G ] kommutativ.

Hvis H er en undergruppe af G , så er R [ H ] en frembringelse af R [ G ]. På samme måde, hvis S er en subring af R , er S [ G ] en subring af R [ G ].

Hvis G er en begrænset rækkefølge større end 1, har R [ G ] altid nul divisorer . Overvej f.eks. Et element g i G af orden | g | = m> 1. Så er 1 - g en nuldeler:

${\ displaystyle (1-g) (1+g+\ cdots+g^{m-1}) = 1-g^{m} = 1-1 = 0.}$

Overvej f.eks. Gruppering Z [ S ₃ ] og elementet i rækkefølge 3 g = (123). I dette tilfælde,

${\ displaystyle (1- (123)) (1+ (123)+(132)) = 1- (123)^{3} = 1-1 = 0.}$

Et beslægtet resultat: Hvis gruppering er primær , så har G ingen nonidentity -begrænset normal undergruppe (især skal G være uendelig). ${\ displaystyle K [G]}$

Bevis: I betragtning af det kontrapositive , antag at det er en endelig identitet under en ikke -identitet . Tag . Siden for enhver ved vi det derfor . Tager , har vi . Ved normalitet af , pendler med et grundlag for , og derfor ${\ displaystyle H}$${\ displaystyle G}$${\ displaystyle a = \ sum _ {h \ in H} h}$${\ displaystyle hH = H}$${\ displaystyle h \ i H}$${\ displaystyle ha = a}$${\ displaystyle a^{2} = \ sum _ {h \ in H} ha = | H | a}$${\ displaystyle b = | H | \, 1-a}$${\ displaystyle ab = 0}$${\ displaystyle H}$${\ displaystyle a}$${\ displaystyle K [G]}$

${\ displaystyle aK [G] b = K [G] ab = 0}$.

Og vi ser, at det ikke er nul, hvilket viser ikke er prima. Dette viser den oprindelige erklæring. ${\ displaystyle a, b}$${\ displaystyle K [G]}$

Gruppe algebra over en endelig gruppe

Gruppe -algebraer forekommer naturligt i teorien om gruppepræsentationer af begrænsede grupper . Gruppealgebraen K [ G ] over et felt K er i det væsentlige gruppering, idet feltet K indtager ringen. Som et sæt og vektorrum, er det den frie vektorrum på G over feltet K . Det vil sige for x i K [ G ],

${\ displaystyle x = \ sum _ {g \ i G} a_ {g} g.}$

Den algebra struktur på vektoren rum er defineret ved hjælp af multiplikation i gruppen:

${\ displaystyle g \ cdot h = gh,}$

hvor g og h til venstre angiver elementer i gruppealgebraen, mens multiplikationen til højre er gruppeoperationen (betegnet ved sidestilling).

Fordi ovenstående multiplikation kan være forvirrende, kan man også skrive basisvektorerne for K [ G ] som e _g (i stedet for g ), i hvilket tilfælde multiplikationen skrives som:

${\ displaystyle e_ {g} \ cdot e_ {h} = e_ {gh}.}$

Fortolkning som funktioner

Når man tænker på det frie vektorrum som K -værdsatte funktioner på G , er algebra -multiplikationen en konvolution af funktioner.

Mens gruppegruppen for en endelig gruppe kan identificeres med funktionsrummet på gruppen, er disse for en uendelig gruppe forskellige. Gruppen algebra, der består af begrænsede summer, svarer til funktioner på gruppen, der forsvinder for uendeligt mange punkter; topologisk (ved hjælp af den diskrete topologi ) svarer disse til funktioner med kompakt støtte .

Gruppealgebraen K [ G ] og funktionsrummet K ^G  : = Hom ( G , K ) er imidlertid to: givet et element i gruppealgebraen

${\ displaystyle x = \ sum _ {g \ i G} a_ {g} g}$

og en funktion på gruppen f  : G → K disse par for at give et element af K via

${\ displaystyle (x, f) = \ sum _ {g \ i G} a_ {g} f (g),}$

hvilket er en veldefineret sum, fordi den er endelig.

Repræsentationer af en gruppealgebra

Når man tager K [ G ] til at være en abstrakt algebra, kan man bede om repræsentationer af algebraen, der virker på et K- vektorrum V af dimension d . Sådan en repræsentation

${\ displaystyle {\ tilde {\ rho}}: K [G] \ højre pil {\ mbox {End}} (V)}$

er en algebra homomorfi fra gruppen algebra til algebra af endomorphisms af V , som er isomorf med ringen af d × d matricer: . Ækvivalent, er dette en venstre K [ G ] -modul over abelsk gruppe V . ${\ displaystyle \ mathrm {End} (V) \ cong M_ {d} (K)}$

Tilsvarende en gruppe repræsentation

${\ displaystyle \ rho: G \ rightarrow {\ mbox {Aut}} (V),}$

er en gruppehomomorfi fra G til gruppen af lineære automorphisms af V , som er isomorf til den generelle lineære gruppe af invertible matricer: . Enhver sådan repræsentation fremkalder en algebra -repræsentation ${\ displaystyle \ mathrm {Aut} (V) \ cong \ mathrm {GL} _ {d} (K)}$

${\ displaystyle {\ tilde {\ rho}}: K [G] \ højre pil {\ mbox {End}} (V),}$

simpelthen ved at lade og udvide lineært. Således svarer repræsentationer af gruppen nøjagtigt til repræsentationer af algebraen, og de to teorier er i det væsentlige ækvivalente. ${\ displaystyle {\ tilde {\ rho}} (e_ {g}) = \ rho (g)}$

Regelmæssig repræsentation

Gruppen algebra er en algebra over sig selv; under korrespondance mellem repræsentationer over R- og R [ G ] -moduler er det gruppens regelmæssige repræsentation .

Skrevet som en repræsentation er det repræsentationen g ↦ ρ _g med handlingen givet af , eller ${\ displaystyle \ rho (g) \ cdot e_ {h} = e_ {gh}}$

${\ displaystyle \ rho (g) \ cdot r = \ sum _ {h \ i G} k_ {h} \ rho (g) \ cdot e_ {h} = \ sum _ {h \ i G} k_ {h} e_ {gh}.}$

Halvdelen af ​​nedbrydning

Dimensionen af ​​vektorrummet K [ G ] er lige lig med antallet af elementer i gruppen. Feltet K bruges normalt til at være de komplekse tal C eller realerne R , så man diskuterer gruppealgerne C [ G ] eller R [ G ].

Gruppen algebra C [ G ] i en endelig gruppe over de komplekse tal er en halvenkel ring . Dette resultat, Maschke sætning , giver os mulighed for at forstå C [ G ] som et endeligt produkt af matrix ringe med indgange i C . Faktisk, hvis vi angiver de komplekse ureducerbare repræsentationer af G som V _k for k = 1,. . . , m , disse svarer til gruppehomomorfier og dermed til algebrahomomorfismer . Samling af disse kortlægninger giver en algebra -isomorfisme${\ displaystyle \ rho _ {k}: G \ til \ mathrm {Aut} (V_ {k})}$${\ displaystyle {\ tilde {\ rho}} _ {k}: \ mathbb {C} [G] \ to \ mathrm {End} (V_ {k})}}$

${\ displaystyle {\ tilde {\ rho}}: \ mathbb {C} [G] \ to \ bigoplus _ {k = 1}^{m} \ mathrm {End} (V_ {k}) \ cong \ bigoplus _ {k = 1}^{m} M_ {d_ {k}} (\ mathbb {C}),}$

hvor d _k er dimensionen af V _k . Subalgebraen for C [ G ] svarende til End ( V _k ) er det tosidede ideal, der genereres af idempotent

${\ displaystyle \ epsilon _ {k} = {\ frac {d_ {k}} {| G |}} \ sum _ {g \ i G} \ chi _ {k} (g^{-1}) \, g,}$

hvor er karakteren af V _k . Disse danner et komplet system af ortogonale idempotents, således at , for j ≠ k , og . Isomorfismen er nært beslægtet med Fourier -transformation på begrænsede grupper . ${\ displaystyle \ chi _ {k} (g) = \ mathrm {tr} \, \ rho _ {k} (g)}$${\ displaystyle \ epsilon _ {k}^{2} = \ epsilon _ {k}}$${\ displaystyle \ epsilon _ {j} \ epsilon _ {k} = 0}$${\ displaystyle 1 = \ epsilon _ {1} +\ cdots +\ epsilon _ {m}}$${\ displaystyle {\ tilde {\ rho}}}$

For et mere generelt felt K, når karakteristikken for K ikke deler rækkefølgen for gruppen G , så er K [ G ] halvenkelt. Når G er en endelig abelsk gruppe , er gruppering K [G] kommutativ, og dens struktur er let at udtrykke i form af enhedens rødder .

Når K er et felt med karakteristisk p, der deler rækkefølgen af G , er gruppering ikke halvenkelt: den har en ikke-nul Jacobson-radikal , og dette giver det tilsvarende emne for modulær repræsentationsteori sin egen, dybere karakter.

Center for en gruppealgebra

Den centrum af gruppen algebra er det sæt af elementer, der pendler med alle elementer i gruppen algebra:

${\ displaystyle \ mathrm {Z} (K [G]): = \ venstre \ {z \ i K [G]: \ forall r \ i K [G], zr = rz \ højre \}.}$

Centret er lig med sættet med klassefunktioner , det er det sæt af elementer, der er konstante på hver konjugeringsklasse

${\ displaystyle \ mathrm {Z} (K [G]) = \ venstre \ {\ sum _ {g \ i G} a_ {g} g: \ forall g, h \ i G, a_ {g} = a_ { h^{-1} gh} \ right \}.}$

Hvis K = C , danner mængden af ureducerbare tegn i G et orthonormalt grundlag for Z ( K [ G ]) med hensyn til det indre produkt

${\ displaystyle \ left \ langle \ sum _ {g \ in G} a_ {g} g, \ sum _ {g \ in G} b_ {g} g \ right \ rangle = {\ frac {1} {| G |}} \ sum _ {g \ i G} {\ bar {a}} _ {g} b_ {g}.}$

Gruppen ringer over en uendelig gruppe

Meget mindre kendes i det tilfælde, hvor G er uendelig eller utallig, og dette er et område med aktiv forskning. Tilfældet, hvor R er feltet for komplekse tal, er sandsynligvis det, der bedst studeres. I dette tilfælde beviste Irving Kaplansky , at hvis a og b er elementer i C [ G ] med ab = 1 , så er ba = 1 . Om dette er sandt, hvis R er et felt med positiv karakteristik, er uvist.

En mangeårig formodning om Kaplansky (~ 1940) siger, at hvis G er en torsionsfri gruppe , og K er et felt, så har gruppering K [ G ] ingen ikke-trivielle nuldelere . Denne formodning er ækvivalent med K [ G ] der ikke har nogen ikke-trivielle nilpotents under samme hypoteser for K og G .

Faktisk kan betingelsen om, at K er et felt, slækkes til enhver ring, der kan indlejres i et integreret domæne .

Formodningen forbliver åben i fuld generalitet, men nogle særlige tilfælde af torsionsfrie grupper har vist sig at tilfredsstille nuldeler-formodningen. Disse omfatter:

• Unikke produktgrupper (f.eks. Grupper , der kan bestilles , især gratis grupper )
• Elementære modtagelige grupper (f.eks. Praktisk talt abelske grupper )
• Diffuse grupper -især grupper, der handler frit isometrisk på R -træer, og de grundlæggende grupper af overfladegrupper bortset fra de grundlæggende grupper af direkte summer på en, to eller tre kopier af det projektive plan.

Tilfældet, hvor G er en topologisk gruppe , diskuteres mere detaljeret i artiklen Gruppealgebra for en lokalt kompakt gruppe .

Kategoriteori

Tilstødende

Kategorisk , gruppen ring konstruktion er venstre adjungerede til " gruppe af enheder "; følgende funktioner er et sammenhængende par :

${\ displaystyle R [-] \ colon \ mathbf {Grp} \ til R \ mathbf {{\ text {-}} Alg}}$

${\ displaystyle (-)^{\ times} \ colon R \ mathbf {{\ text {-}} Alg} \ to \ mathbf {Grp}}$

hvor tager en gruppe til sin gruppering over R , og tager en R -algebra til sin gruppe af enheder. ${\ displaystyle R [-]}$${\ displaystyle (-)^{\ times}}$

Når R = Z , giver dette et supplement mellem kategorien af ​​grupper og kategorien af ​​ringe , og adjektionens enhed tager en gruppe G til en gruppe, der indeholder trivielle enheder: G × {± 1} = {± g }. Generelt indeholder grupperinge ikke -private enheder. Hvis G indeholder elementerne a og b sådan, at og b ikke normaliseres, er kvadratet af ${\ displaystyle a^{n} = 1}$${\ displaystyle \ langle a \ rangle}$

${\ displaystyle x = (a-1) b \ venstre (1+a+a^{2}+...+a^{n-1} \ højre)}$

er nul, derfor . Elementet 1 + x er en enhed af uendelig rækkefølge. ${\ displaystyle (1+x) (1-x) = 1}$

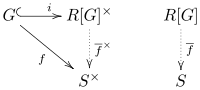
Universel ejendom

Ovenstående tillæg udtrykker en universel egenskab ved grupperinge. Lad R være en (kommutativ) ring, lad G være en gruppe, og lad S være en R -algebra. For enhver gruppehomomorfisme findes der en unik R -algebrahomomorfisme, så hvor i er inklusionen ${\ displaystyle f: G \ til S^{\ times}}$${\ displaystyle {\ overline {f}}: R [G] \ til S}$${\ displaystyle {\ overline {f}} \ circ i = f}$

${\ displaystyle {\ begin {align} i: G & \ longrightarrow R [G] \\ g & \ longmapsto 1_ {R} g \ end {align}}}$

Med andre ord er den unikke homomorfisme, der får følgende diagram til at pendle: ${\ displaystyle {\ overline {f}}}$

Enhver anden ring, der opfylder denne egenskab, er kanonisk isomorf for gruppering.

Hopf algebra

Gruppen algebra K [ G ] har en naturlig struktur af en Hopf -algebra . Komultiplikationen er defineret af , forlænget lineært, og antipoden forlænges igen lineært. ${\ displaystyle \ Delta (g) = g \ otimes g}$${\ displaystyle S (g) = g^{-1}}$

Generaliseringer

Gruppen algebra generaliserer til monoidringen og derfra til kategorien algebra , hvoraf et andet eksempel er forekomstalgebraen .

Filtrering

Hvis en gruppe har en længdefunktion - for eksempel hvis der er et valg af generatorer, og man tager ordet metrisk , som i Coxeter -grupper - så bliver gruppering til en filtreret algebra .

Se også

• Gruppealgebra af en lokalt kompakt gruppe
• Monoid ring

Repræsentationsteori

• Gruppens repræsentation
• Regelmæssig repræsentation

Kategoriteori

• Kategorisk algebra
• Gruppe af enheder
• Incident algebra
• Quiver algebra

Noter

Referencer

• AA Bovdi (2001) [1994], "Group algebra" , Encyclopedia of Mathematics , EMS Press
• Milies, César Polcino; Sehgal, Sudarshan K. En introduktion til grupperinge . Algebras og applikationer, bind 1. Springer, 2002. ISBN  978-1-4020-0238-0
• Charles W. Curtis , Irving Reiner . Repræsentationsteori for begrænsede grupper og associative algebraer , Interscience (1962)
• DS Passman, Den algebraiske struktur af grupperinge , Wiley (1977)