Invariant (matematik) - Invariant (mathematics)

Et tapet er uforanderligt under et uendeligt antal  oversættelser , medlemmer af en gruppe , hvoraf operationen betegnet med er funktionssammensætningen .${\ displaystyle \ circ}$

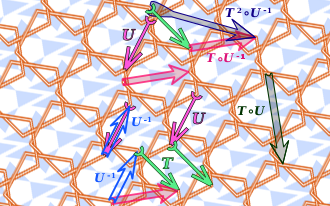
I matematik er en invariant en egenskab for et matematisk objekt (eller en klasse af matematiske objekter), der forbliver uændret, efter at operationer eller transformationer af en bestemt type er anvendt på objekterne. Den særlige klasse af objekter og typen af ​​transformationer er normalt angivet ved den sammenhæng, hvori udtrykket bruges. For eksempel er arealet af en trekant en invariant med hensyn til isometrier af det euklidiske plan . Udtrykkene "invariant under" og "invariant til" en transformation bruges begge. Mere generelt er en invariant med hensyn til en ækvivalensrelation en egenskab, der er konstant på hver ækvivalensklasse .

Invarianter bruges i forskellige områder af matematik som geometri , topologi , algebra og diskret matematik . Nogle vigtige klasser af transformation er defineret af en uforanderlig, de efterlader uændret. For eksempel er konforme kort defineret som transformationer af planet, der bevarer vinkler . Opdagelsen af ​​invarianter er et vigtigt skridt i processen med at klassificere matematiske objekter.

Eksempler

Et simpelt eksempel på uforanderlighed udtrykkes i vores evne til at tælle . For et endeligt sæt objekter af enhver art er der et nummer, som vi altid kommer til, uanset rækkefølgen , hvor vi tæller objekterne i sættet . Mængden - et hovednummer - er knyttet til sættet og er uændret under tællingsprocessen.

En identitet er en ligning, der forbliver sand for alle værdier af dens variabler. Der er også uligheder, der forbliver sande, når værdierne af deres variabler ændres.

Den afstand mellem to punkter på en række linje ændres ikke ved at tilføje den samme mængde til begge numre. På den anden side har multiplikation ikke den samme egenskab, da afstand ikke er uforanderlig under multiplikation.

Afstandens vinkler og forhold er uforanderlige under skaleringer , rotationer , oversættelser og refleksioner . Disse transformationer producerer lignende former, som er grundlaget for trigonometri . I modsætning hertil er vinkler og forhold ikke uforanderlige under ikke-ensartet skalering (såsom strækning). Summen af ​​en trekants indvendige vinkler (180 °) er uforanderlig under alle ovenstående operationer. Som et andet eksempel er alle cirkler ens: de kan omdannes til hinanden, og forholdet mellem omkredsen og diameteren er uændret (betegnet med det græske bogstav π ( pi )).

Nogle mere komplicerede eksempler:

• Den reelle del og den absolutte værdi af et komplekst tal er uforanderlige under kompleks konjugation .
• Den grad af et polynomium er invariant under en lineær ændring af variable.
• De dimension og homologigrupper af en topologisk objekt er invariant under homeomorfi .
• Antallet af faste punkter i et dynamisk system er uforanderligt under mange matematiske operationer.
• Euklidisk afstand er uforanderlig under ortogonale transformationer .
• Det euklidiske område er uforanderligt under lineære kort, der har determinant ± 1 (se Ækviarealkort § Lineære transformationer ).
• Nogle invarianter af projektive transformationer inkluderer kollinearitet på tre eller flere punkter, samtidighed på tre eller flere linjer, koniske sektioner , krydsforholdet .
• De determinant , trace og egenvektorer og egenværdier af en kvadratisk matrix er invariant under ændringer i basis . Med andre ord er spektret af en matrix uændret i forhold til grundændringen.
• De vigtigste invarianter af tensorer ændres ikke med rotation af koordinatsystemet (se Invarianter af tensorer ).
• De singulære værdier af en matrix er invariant under ortogonale transformationer.
• Lebesgue-foranstaltning er uforanderlig under oversættelser.
• Den varians af en sandsynlighedsfordeling er invariant under oversættelser af reelle akse ; derfor er variansen af ​​en tilfældig variabel uændret efter tilføjelsen af ​​en konstant.
• De faste punkter i en transformation er de elementer i domænet, der er uforanderlige under transformationen. De kan, afhængigt af applikationen, kaldes symmetriske med hensyn til denne transformation. For eksempel er objekter med translationel symmetri uændrede under visse oversættelser.
• Den integrerede del af den Gaussiske krumning af en 2-dimensionel Riemannian manifold er uforanderlig under ændringer af den Riemanniske metriske . Dette er Gauss – Bonnet sætningen .${\ textstyle \ int _ {M} K \, d \ mu}$${\ displaystyle K}$ ${\ displaystyle (M, g)}$ ${\ displaystyle g}$
• Differentielle invarianter til differentialligninger

MU-puslespil

Den MU puslespil er et godt eksempel på et logisk problem, hvor bestemme en invariant er brug for en umulighed bevis . Puslespillet beder en om at starte med ordet MI og omdanne det til ordet MU ved at bruge i hvert trin en af ​​følgende transformationsregler:

1. Hvis en streng slutter med et I, kan der tilføjes en U ( x I → x IU)
2. Strengen efter M kan være fuldstændigt duplikeret (M x → M xx )
3. Enhver tre på hinanden følgende I'er (III) kan erstattes med en enkelt U ( x III y → x U y )
4. Enhver to på hinanden følgende U'er kan fjernes ( x UU y → xy )

Et eksempel på afledning (med overskrifter, der angiver de anvendte regler) er

MI → ² MII → ² MIIII → ³ MUI → ² MUIUI → ¹ MUIUIU → ² MUIUIUUUU → ⁴ MUIUIIUIU → ...

I lyset af dette kan man undre sig over, om det er muligt at konvertere MI til MU ved kun at bruge disse fire transformationsregler. Man kunne bruge mange timer på at anvende disse transformationsregler på strenge. Det kan dog være hurtigere at finde en ejendom, der er uforanderlig for alle regler (dvs. der ikke ændres af nogen af ​​dem), og viser, at det er umuligt at komme til MU. Ved at se puslespillet fra et logisk synspunkt kan man indse, at den eneste måde at slippe af med nogen jeg er, er at have tre på hinanden følgende jeg i strengen. Dette gør følgende uændrede interessante at overveje:

Antallet af I'er i strengen er ikke et multiplum af 3 .

Dette er en invariant til problemet, hvis følgende gælder for hver af transformationsreglerne: hvis invarianten holdes inden anvendelsen af ​​reglen, vil den også holde efter anvendelse af den. Ser man på nettoeffekten af ​​at anvende reglerne på antallet af I'er og U'er, kan man se, at dette faktisk er tilfældet for alle regler:

Herske	#Er	#Os	Effekt på invariant
1	+0	+1	Antal I'er er uændret. Hvis invarianten holdt, gør det stadig.
2	× 2	× 2	Hvis n ikke er et multiplum af 3, er 2 × n heller ikke. Den uforanderlige holder stadig.
3	−3	+1	Hvis n ikke er et multiplum af 3, er n -3 heller ikke. Den uforanderlige holder stadig.
4	+0	−2	Antal I'er er uændret. Hvis invarianten holdt, gør det stadig.

Ovenstående tabel viser tydeligt, at invarianten holder for hver af de mulige transformationsregler, hvilket betyder, at hvilken som helst regel man vælger, uanset hvilken tilstand, hvis antallet af I ikke var et multiplum af tre inden anvendelsen af ​​reglen, så vil det ikke være bagefter enten.

I betragtning af at der er et enkelt I i startstrengen MI, og en der ikke er et multiplum af tre, kan man derefter konkludere, at det er umuligt at gå fra MI til MU (da antallet af I'er aldrig vil være et multiplum af tre ).

Invariant sæt

En delmængde S af domænet U af en kortlægning T : U → U er en invariant sæt under kortlægningen når Bemærk, at de elementer i S ikke er fast , selv om den indstillede S er fastgjort i indstillede effekt af U . (Nogle forfattere bruger terminologien setvis invariant versus punktvis invariant for at skelne mellem disse tilfælde.) For eksempel er en cirkel en invariant delmængde af planet under en rotation omkring cirkelens centrum. Yderligere er en konisk overflade uændret som et sæt under en homøthet af rummet. ${\ displaystyle x \ i S \ antyder T (x) \ i S.}$

En invariant sæt af en operation T siges også at være stabile under T . For eksempel er de normale undergrupper, der er så vigtige i gruppeteorien , de undergrupper, der er stabile under den indre automorfisme i den omgivende gruppe . I lineær algebra , hvis en lineær transformation T har en egenvektor v , så linien gennem 0 , og v er et invariant sæt under T , i hvilket tilfælde egenvektorerne spænde en invariant underrum , som er stabil under T .

Når T er en skrueforskydning , er skrueaksen en uforanderlig linje, men hvis tonehøjden ikke er nul, har T ingen faste punkter.

Formel erklæring

Begrebet invarians formaliseres på tre forskellige måder i matematik: via gruppeaktioner , præsentationer og deformation.

Uændret under gruppeaktion

For det første, hvis man har en gruppe G, der virker på et matematisk objekt (eller et sæt objekter) X, så kan man spørge, hvilke punkter x der er uændrede, "uændrede" under gruppehandlingen eller under et element g i gruppen.

Ofte vil man have en gruppe, der virker på et sæt X , hvilket efterlader en til at bestemme, hvilke objekter i et tilknyttet sæt F ( X ) er uforanderlige. For eksempel efterlader rotation i planet omkring et punkt det punkt, som det roterer om, uvarant, mens oversættelse i flyet ikke efterlader nogen punkter invariant, men efterlader alle linjer parallelt med retningen af ​​translation invariant som linjer. Definér formelt linjesættet i planet P som L ( P ); så tager en stiv bevægelse af planet linjer til linjer - gruppen af ​​stive bevægelser virker på linjesættet - og man kan spørge, hvilke linjer der er uændrede ved en handling.

Endnu vigtigere kan man definere en funktion på et sæt, såsom "radius af en cirkel i planet", og derefter spørge, om denne funktion er uforanderlig under en gruppehandling, såsom stive bevægelser.

Dobbelt med begrebet invarianter er møntvarianter , også kendt som baner, som formaliserer forestillingen om kongruens : objekter, der kan føres til hinanden ved en gruppeaktion. For eksempel, under gruppen af ​​stive bevægelser af planet, er omkredsen af en trekant en invariant, mens sættet af trekanter, der er kongruente til en given trekant, er en møntvariant.

Disse er forbundet som følger: invarianter er konstante på møntvarianter (for eksempel har kongruente trekanter samme omkreds), mens to objekter, der er enige i værdien af ​​en invariant, måske eller måske ikke er kongruente (for eksempel to trekanter med samme omkreds behøver ikke at være kongruent). I klassificeringsproblemer kan man søge at finde et komplet sæt invarianter , således at hvis to objekter har de samme værdier for dette sæt invarianter, så er de kongruente.

For eksempel er trekanter, således at alle tre sider er ens, kongruente under stive bevægelser via SSS-kongruens , og således danner længderne på alle tre sider et komplet sæt invarianter til trekanter. De tre vinkelmål i en trekant er også uforanderlige under stive bevægelser, men danner ikke et komplet sæt, da inkongruente trekanter kan dele de samme vinkelmål. Men hvis man tillader skalering ud over stive bevægelser, viser AAA-lighedskriteriet imidlertid , at dette er et komplet sæt af invarianter.

Uafhængig af præsentationen

For det andet kan en funktion defineres i form af en vis præsentation eller nedbrydning af et matematisk objekt; for eksempel er Euler-karakteristikken for et cellekompleks defineret som den alternerende sum af antallet af celler i hver dimension. Man kan glemme cellekompleksstrukturen og kun se på det underliggende topologiske rum ( manifolden ) - da forskellige cellekomplekser giver den samme underliggende manifold, kan man spørge, om funktionen er uafhængig af valg af præsentation, i hvilket tilfælde den er iboende defineret invariant. Dette er tilfældet for Euler-karakteristikken, og en generel metode til at definere og beregne invarianter er at definere dem til en given præsentation og derefter vise, at de er uafhængige af valget af præsentation. Bemærk, at der ikke er nogen forestilling om en gruppehandling i denne forstand.

De mest almindelige eksempler er:

• Den præsentation af en manifold med hensyn til at koordinere diagrammer - invarianter skal være uændret under forandring af koordinater .
• Forskellige mangfoldige nedbrydninger , som diskuteret for Eulers karakteristiske.
• Varianter af en præsentation af en gruppe .

Uændret under forstyrrelse

For det tredje, hvis man studerer et objekt, der varierer i en familie, som det er almindeligt i algebraisk geometri og differentiel geometri , kan man spørge, om ejendommen er uændret under forstyrrelse (for eksempel hvis et objekt er konstant på familier eller invariant under ændring af metrisk).

Invarianter inden for datalogi

I datalogi kan man støde på invarianter, som man kan stole på for at være sande under udførelsen af ​​et program eller under en del af det. Det er en logisk påstand , der altid anses for at være sand i en bestemt fase af udførelsen. For eksempel er en loop-invariant en betingelse, der er sand i begyndelsen og slutningen af ​​hver udførelse af en loop.

Invarianter er især nyttige, når man tænker over, om et computerprogram er korrekt. Teorien om optimering af kompilatorer , metodikken for design efter kontrakt og formelle metoder til bestemmelse af programkorrekthed er alt afhængig af invarianter.

Programmører bruger ofte påstande i deres kode for at gøre invarianter eksplicitte. Nogle objektorienterede programmeringssprog har en særlig syntaks til angivelse af klasseinvarianter .

Automatisk invariant detektion i tvingende programmer

Abstrakte fortolkningsværktøjer kan beregne enkle invarianter af givne vigtige computerprogrammer. Hvilke egenskaber der kan findes afhænger af de anvendte abstrakte domæner . Typiske eksempler på egenskaber er intervaller med et enkelt heltal som f.eks 0<=x<1024. Forholdet mellem flere variabler 0<=i-j<2*n-1og modulusinformation som y%4==0. Akademiske forskningsprototyper overvejer også enkle egenskaber ved markørstrukturer.

Mere sofistikerede invarianter skal generelt leveres manuelt. Især når der verificeres et bydende program ved hjælp af Hoare-beregningen , skal der tilvejebringes en loop-invariant manuelt for hver loop i programmet, hvilket er en af ​​grundene til, at denne tilgang generelt er upraktisk for de fleste programmer.

I forbindelse med ovenstående MU-puslespileksempel er der i øjeblikket ikke noget generelt automatiseret værktøj, der kan registrere, at en afledning fra MI til MU kun er umulig ved kun at bruge reglerne 1–4. Når først abstraktionen fra strengen til nummeret på dens "I" er lavet manuelt, hvilket f.eks. Fører til det følgende C-program, vil et abstrakt fortolkningsværktøj være i stand til at detektere, der ICount%3ikke kan være 0, og dermed "mens" -løkken vil aldrig ophøre.

void MUPuzzle(void) {
    volatile int RandomRule;
    int ICount = 1, UCount = 0;
    while (ICount % 3 != 0)                         // non-terminating loop
        switch(RandomRule) {
        case 1:                  UCount += 1;   break;
        case 2:   ICount *= 2;   UCount *= 2;   break;
        case 3:   ICount -= 3;   UCount += 1;   break;
        case 4:                  UCount -= 2;   break;
        }                                          // computed invariant: ICount % 3 == 1 || ICount % 3 == 2
}

Se også

Bemærkninger

Referencer

eksterne links

• "Applet: Visual Invariants in Sorting Algorithms" af William Braynen i 1997