Lineært kort - Linear map

I matematik , og mere specifikt i lineær algebra , er et lineært kort (også kaldet en lineær kortlægning , lineær transformation , vektorrumshomomorfisme eller i nogle sammenhænge lineær funktion ) en kortlægning mellem to vektorrum, der bevarer operationerne af vektortilsætning og skalar multiplikation . De samme navne og den samme definition bruges også til det mere generelle tilfælde af moduler over en ring ; se modul homomorfisme . ${\ displaystyle V \ til W}$

Hvis et lineært kort er en bijektion, kaldes det en lineær isomorfisme . I det tilfælde, hvor et lineært kort kaldes en (lineær) endomorfisme . Nogle gange refererer udtrykket lineær operator til dette tilfælde, men udtrykket "lineær operator" kan have forskellige betydninger for forskellige konventioner: det kan for eksempel bruges til at understrege det og er reelle vektorrum (ikke nødvendigvis med ), eller det kan være bruges til at understrege, at det er et funktionsrum , som er en almindelig konvention i funktionel analyse . Nogle gange har udtrykket lineær funktion samme betydning som lineært kort , mens det i analyse ikke gør det. ${\ displaystyle V = W}$${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle V = W}$${\ displaystyle V}$

En lineær afbildning fra V til W kortlægger altid oprindelsen af V til oprindelsen af W . Desuden kortlægger den lineære underrum i V til lineære underrum i W (muligvis af en lavere dimension ); for eksempel den rummer et plan gennem oprindelse i V til enten et plan gennem oprindelse i W , en linje gennem oprindelsen i W , eller bare oprindelsen i W . Lineære kort kan ofte repræsenteres som matricer , og enkle eksempler omfatter rotation og refleksion lineære transformationer .

På det sprog, kategori teori , lineære afbildninger er morfier af vektorrum.

Definition og første konsekvenser

Lad og vær vektorrum over det samme felt . En funktion siges at være et lineært kort, hvis for to vektorer og enhver skalar følgende to betingelser er opfyldt: ${\ displaystyle V}$${\ displaystyle W}$ ${\ displaystyle K}$${\ displaystyle f: V \ til W}$${\ textstyle \ mathbf {u}, \ mathbf {v} \ in V}$${\ displaystyle c \ i K}$

Additivitet / drift af tilsætning

${\ displaystyle f (\ mathbf {u} +\ mathbf {v}) = f (\ mathbf {u}) +f (\ mathbf {v})}$

Homogenitet af grad 1 / operation af skalarmultiplikation

${\ displaystyle f (c \ mathbf {u}) = cf (\ mathbf {u})}$

Således siges et lineært kort at være driftsbevarende . Med andre ord er det ligegyldigt, om det lineære kort anvendes før (højre side af ovenstående eksempler) eller efter (eksemplernes venstre side) operationerne med addition og skalarmultiplikation.

Ved associeringsgraden af ​​additionsoperationen betegnet som + gælder følgende lighed for alle vektorer og skalarer : ${\ textstyle \ mathbf {u} _ {1}, \ ldots, \ mathbf {u} _ {n} \ i V}$${\ textstyle c_ {1}, \ ldots, c_ {n} \ i K,}$

Betegner nul elementer i vektorrum og ved og henholdsvis det følger, at Lade og i ligningen for homogenitet grad 1: ${\ displaystyle V}$${\ displaystyle W}$${\ textstyle \ mathbf {0} _ {V}}$${\ textstyle \ mathbf {0} _ {W}}$${\ textstyle f (\ mathbf {0} _ {V}) = \ mathbf {0} _ {W}.}$${\ displaystyle c = 0}$${\ textstyle \ mathbf {v} \ i V}$

Lejlighedsvis og kan være vektorrum over forskellige felter. Det er derefter nødvendigt at specificere, hvilke af disse jordfelter der bruges i definitionen af ​​"lineær". Hvis og er mellemrum over det samme felt som ovenfor, taler vi om -lineariske kort. For eksempel er konjugering af komplekse tal et -linjært kort , men det er ikke -linear, hvor og er symboler, der repræsenterer sæt af reelle tal og komplekse tal, henholdsvis. ${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle K}$${\ displaystyle K}$${\ displaystyle \ mathbb {R}}$${\ displaystyle \ mathbb {C} \ to \ mathbb {C}}$${\ displaystyle \ mathbb {C}}$${\ displaystyle \ mathbb {R}}$${\ displaystyle \ mathbb {C}}$

Et lineært kort med et endimensionelt vektorrum over sig selv kaldes en lineær funktionel . ${\ displaystyle V \ til K}$${\ displaystyle K}$

Disse udsagn generaliserer til ethvert venstre modul over en ring uden ændringer, og til ethvert højre modul ved reversering af skalarmultiplikationen. ${\ textstyle {} _ {R} M}$${\ displaystyle R}$

Eksempler

• Et prototypisk eksempel, der giver lineære kort deres navn, er en funktion , hvoraf grafen er en linje gennem oprindelsen.${\ displaystyle f: \ mathbb {R} \ to \ mathbb {R}: x \ mapsto cx}$
• Mere generelt er enhver homøhed, hvor det er centreret i oprindelsen af ​​et vektorrum, et lineært kort.${\ textstyle \ mathbf {v} \ mapsto c \ mathbf {v}}$${\ displaystyle c}$
• Nulkortet mellem to vektorrum (over det samme felt ) er lineært.${\ textstyle \ mathbf {x} \ mapsto \ mathbf {0}}$
• Den identitet kort på enhver modul er en lineær operator.
• For reelle tal er kortet ikke lineært.${\ textstyle x \ mapsto x^{2}}$
• For reelle tal er kortet ikke lineært (men er en affin transformation ).${\ textstyle x \ mapsto x+1}$
• Hvis er en reel matrix , definerer derefter et lineært kort fra til ved at sende en kolonnevektor til kolonnevektoren . Omvendt kan ethvert lineært kort mellem endelige-dimensionelle vektorrum repræsenteres på denne måde; se § Matricer nedenfor.${\ displaystyle A}$${\ displaystyle m \ gange n}$ ${\ displaystyle A}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle \ mathbb {R} ^{m}}$ ${\ displaystyle \ mathbf {x} \ in \ mathbb {R} ^{n}}$${\ displaystyle A \ mathbf {x} \ in \ mathbb {R} ^{m}}$
• Hvis er en isometri mellem virkelige normerede rum , så er der et lineært kort. Dette resultat er ikke nødvendigvis sandt for komplekse normerede rum.${\ textstyle f: V \ til W}$${\ textstyle f (0) = 0}$${\ displaystyle f}$
• Differentiering definerer et lineært kort fra rummet for alle differentierbare funktioner til rummet af alle funktioner. Det definerer også en lineær operator i rummet for alle glatte funktioner (en lineær operator er en lineær endomorfisme , det er et lineært kort, hvor domænet og kodomænet for det er det samme). Et eksempel er
  $${\ displaystyle {\ frac {d} {dx}} \ venstre (c_ {1} f_ {1} (x)+c_ {2} f_ {2} (x)+\ cdots+c_ {n} f_ {n } (x) \ højre) = c_ {1} {\ frac {df_ {1} (x)} {dx}}+c_ {2} {\ frac {df_ {2} (x)} {dx}}+ \ cdots +c_ {n} {\ frac {df_ {n} (x)} {dx}}.}$$

  
• En bestemt integral over et eller andet interval I er et lineært kort fra rummet for alle reelt værdsatte integrerbare funktioner på I til . For eksempel,${\ displaystyle \ mathbb {R}}$
  $${\ displaystyle \ int _ {a}^{b} {\ venstre [c_ {1} f_ {1} (x)+c_ {2} f_ {2} (x)+\ dots+c_ {n} f_ { n} (x) \ højre] dx} = {c_ {1} \ int _ {a}^{b} f_ {1} (x) \, dx}+{c_ {2} \ int _ {a}^ {b} f_ {2} (x) \, dx} +\ cdots +{c_ {n} \ int _ {a}^{b} f_ {n} (x) \, dx}.}$$

  
• En ubestemt integral (eller antiderivativ ) med et fast integrationsudgangspunkt definerer et lineært kort fra rummet med alle reelt værdsatte integrerbare funktioner til rummet med alle reelt værdsatte, differentierbare funktioner på . Uden et fast udgangspunkt mapper antiderivative sig til kvotrummet for de differentierbare funktioner ved hjælp af det lineære rum med konstante funktioner.${\ displaystyle \ mathbb {R}}$${\ displaystyle \ mathbb {R}}$
• Hvis og er endelige-dimensionelle vektorrum over et felt F med respektive dimensioner m og n , så er funktionen, der kortlægger lineære kort til n × m matricer på den måde, der er beskrevet i § Matricer (nedenfor), et lineært kort, og endda en lineær isomorfisme .${\ displaystyle V}$${\ displaystyle W}$${\ textstyle f: V \ til W}$
• Den forventede værdi af en tilfældig variabel (som faktisk er en funktion og som sådan et element i et vektorrum) er lineær, som for tilfældige variabler, og vi har og , men variansen af en tilfældig variabel er ikke lineær.${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle E [X+Y] = E [X]+E [Y]}$${\ displaystyle E [aX] = aE [X]}$

• 

  Funktionen med er et lineært kort. Denne funktion skalerer komponenten i en vektor med faktoren . ${\ textstyle f: \ mathbb {R} ^{2} \ to \ mathbb {R} ^{2}}$${\ textstyle f (x, y) = (2x, y)}$${\ textstyle x}$${\ textstyle 2}$

• 

  Funktionen er additiv: Det er ligegyldigt, om vektorer først tilføjes og derefter kortlægges, eller om de kortlægges og til sidst tilføjes:${\ textstyle f (x, y) = (2x, y)}$${\ textstyle f (\ mathbf {a} +\ mathbf {b}) = f (\ mathbf {a}) +f (\ mathbf {b})}}$

• 

  Funktionen er homogen: Det er ligegyldigt, om en vektor først skaleres og derefter kortlægges eller først kortlægges og derefter skaleres:${\ textstyle f (x, y) = (2x, y)}$${\ textstyle f (\ lambda \ mathbf {a}) = \ lambda f (\ mathbf {a})}$

Matricer

Hvis og er endelige-dimensionelle vektorrum, og der er defineret et grundlag for hvert vektorrum, kan hvert lineært kort fra til repræsenteres af en matrix . Dette er nyttigt, fordi det tillader konkrete beregninger. Matricer giver eksempler på lineære kort: hvis er en ægte matrix, beskriver den derefter et lineært kort (se Euklidisk rum ). ${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle A}$${\ displaystyle m \ gange n}$${\ displaystyle f (\ mathbf {x}) = A \ mathbf {x}}$${\ displaystyle \ mathbb {R} ^{n} \ to \ mathbb {R} ^{m}}$

Lad være et grundlag for . Derefter bestemmes hver vektor entydigt af koefficienterne i feltet : ${\ displaystyle \ {{\ mathbf {v}} _ {1}, \ ldots, {\ mathbf {v}} _ {n} \}}$${\ displaystyle V}$${\ displaystyle {\ mathbf {v}} \ i V}$${\ displaystyle {\ mathbf {c}} _ {1}, \ ldots, {\ mathbf {c}} _ {n}}$${\ displaystyle \ mathbb {R} ^{n}}$

Hvis er et lineært kort, ${\ textstyle f: V \ til W}$

hvilket indebærer, at funktionen f er fuldstændig bestemt af vektorerne . Lad nu være et grundlag for . Derefter kan vi repræsentere hver vektor som ${\ displaystyle f ({\ mathbf {v}} _ {1}), \ ldots, f ({\ mathbf {v}} _ {n})}$${\ displaystyle \ {{\ mathbf {w}} _ {1}, \ ldots, {\ mathbf {w}} _ {m} \}}$${\ displaystyle W}$${\ displaystyle f ({\ mathbf {v}} _ {j})}$

Således bestemmes funktionen fuldstændigt af værdierne for . Hvis vi sætter disse værdier i en matrix , kan vi bekvemt bruge den til at beregne vektoroutput for en hvilken som helst vektor i . For at få , er hver kolonne af en vektor ${\ displaystyle f}$${\ displaystyle a_ {ij}}$${\ displaystyle m \ gange n}$${\ displaystyle M}$${\ displaystyle f}$${\ displaystyle V}$${\ displaystyle M}$${\ displaystyle j}$${\ displaystyle M}$

svarende til som defineret ovenfor. For at definere det mere klart, for en kolonne, der svarer til kortlægningen , ${\ displaystyle f ({\ mathbf {v}} _ {j})}$${\ displaystyle j}$${\ displaystyle f ({\ mathbf {v}} _ {j})}$ hvor er matrixen af . Med andre ord har hver kolonne en tilsvarende vektor, hvis koordinater er elementerne i kolonnen . Et enkelt lineært kort kan repræsenteres af mange matricer. Dette skyldes, at værdierne for elementerne i en matrix afhænger af de valgte baser. ${\ displaystyle M}$${\ displaystyle f}$${\ displaystyle j = 1, \ ldots, n}$${\ displaystyle f ({\ mathbf {v}} _ {j})}$${\ displaystyle a_ {1j} +\ cdots +a_ {mj}}$${\ displaystyle j}$

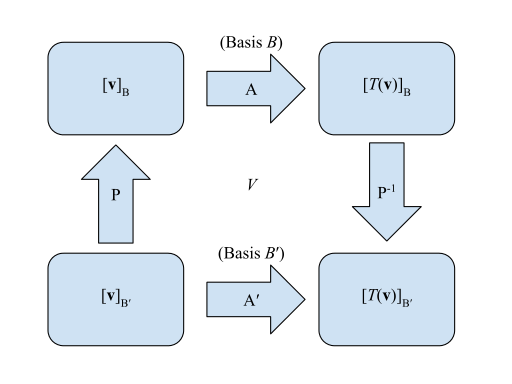
Matricerne for en lineær transformation kan repræsenteres visuelt:

1. Matrix for i forhold til :${\ textstyle T}$${\ textstyle B}$${\ textstyle A}$
2. Matrix for i forhold til :${\ textstyle T}$${\ textstyle B '}$${\ textstyle A '}$
3. Overgangsmatrix fra til :${\ textstyle B '}$${\ textstyle B}$${\ textstyle P}$
4. Overgangsmatrix fra til :${\ textstyle B}$${\ textstyle B '}$${\ textstyle P^{-1}}$

Sådan at man begyndte i nederste venstre hjørne og ledte efter det nederste højre hjørne , ville man multiplicere venstre-det vil sige . Den ækvivalente metode ville være den "længere" metode, der går med uret fra det samme punkt, så der multipliceres med eller . ${\ textstyle \ left [\ mathbf {v} \ right] _ {B '}}$${\ textstyle \ left [T \ left (\ mathbf {v} \ right) \ right] _ {B '}}$${\ tekststil A '\ venstre [\ mathbf {v} \ højre] _ {B'} = \ venstre [T \ venstre (\ mathbf {v} \ højre) \ højre] _ {B '}}$${\ textstyle \ left [\ mathbf {v} \ right] _ {B '}}$${\ textstyle P^{-1} AP}$${\ textstyle P^{-1} AP \ venstre [\ mathbf {v} \ højre] _ {B '} = \ venstre [T \ venstre (\ mathbf {v} \ højre) \ højre] _ {B'} }$

Eksempler i to dimensioner

I to- dimensionalt rum R ² lineære afbildninger er beskrevet af 2 × 2 matricer . Dette er nogle eksempler:

• rotation
  • 90 grader mod uret:
    $${\ displaystyle \ mathbf {A} = {\ begin {pmatrix} 0 & -1 \\ 1 & 0 \ end {pmatrix}}}$$

    
  • i en vinkel θ mod uret:
    $${\ displaystyle \ mathbf {A} = {\ begin {pmatrix} \ cos \ theta &-\ sin \ theta \\\ sin \ theta & \ cos \ theta \ end {pmatrix}}}$$

    
• afspejling
  • gennem x -aksen:
    $${\ displaystyle \ mathbf {A} = {\ begin {pmatrix} 1 & 0 \\ 0 & -1 \ end {pmatrix}}}$$

    
  • gennem y -aksen:
    $${\ displaystyle \ mathbf {A} = {\ begin {pmatrix} -1 & 0 \\ 0 & 1 \ end {pmatrix}}}$$

    
  • gennem en linje, der laver en vinkel θ med oprindelsen:
    $${\ displaystyle \ mathbf {A} = {\ begin {pmatrix} \ cos {2 \ theta} & \ sin {2 \ theta} \\\ sin {2 \ theta} &-\ cos {2 \ theta} \ end {pmatrix}}}$$

    
• skalering med 2 i alle retninger:
  $${\ displaystyle \ mathbf {A} = {\ begin {pmatrix} 2 & 0 \\ 0 & 2 \ end {pmatrix}} = 2 \ mathbf {I}}$$

  
• horisontal forskydningskortlægning :
  $${\ displaystyle \ mathbf {A} = {\ begin {pmatrix} 1 & m \\ 0 & 1 \ end {pmatrix}}}$$

  
• klem kortlægning :
  $${\ displaystyle \ mathbf {A} = {\ begin {pmatrix} k & 0 \\ 0 & {\ frac {1} {k}} \ end {pmatrix}}}$$

  
• projektion på y -aksen:
  $${\ displaystyle \ mathbf {A} = {\ begin {pmatrix} 0 & 0 \\ 0 & 1 \ end {pmatrix}}.}$$

  

Vektorrum af lineære kort

Sammensætningen af ​​lineære kort er lineær: hvis og er lineære, så er deres sammensætning det også . Det følger heraf, at klassen af alle vektorrum over et givet felt K sammen med K -lineære kort som morfisme danner en kategori . ${\ displaystyle f: V \ til W}$${\ textstyle g: W \ til Z}$ ${\ textstyle g \ circ f: V \ til Z}$

Den inverse af en lineær afbildning, når defineret, er igen en lineær afbildning.

Hvis og er lineære, så er deres pointvise sum , som er defineret af . ${\ textstyle f_ {1}: V \ til W}$${\ textstyle f_ {2}: V \ til W}$${\ displaystyle f_ {1}+f_ {2}}$${\ displaystyle (f_ {1}+f_ {2}) (\ mathbf {x}) = f_ {1} (\ mathbf {x})+f_ {2} (\ mathbf {x})}$

Hvis det er lineært og er et element i jordfeltet , så er kortet , defineret af , også lineært. ${\ textstyle f: V \ til W}$${\ textstyle \ alpha}$${\ textstyle K}$${\ textstyle \ alpha f}$${\ textstyle (\ alpha f) (\ mathbf {x}) = \ alpha (f (\ mathbf {x}))}}$

Sættet således af lineære afbildninger fra at selv danner et vektorrum over , undertiden betegnet . I det tilfælde, at dette vektorrum, betegnet , er en associativ algebra under sammensætning af kort , da sammensætningen af ​​to lineære kort igen er et lineært kort, og sammensætningen af ​​kort altid er associativ. Denne sag diskuteres mere detaljeret nedenfor. ${\ textstyle {\ mathcal {L}} (V, W)}$${\ textstyle V}$${\ textstyle W}$${\ textstyle K}$${\ textstyle \ operatorname {Hom} (V, W)}$${\ textstyle V = W}$${\ textstyle \ operatorname {End} (V)}$

I givet fald igen det endelige dimensionelle tilfælde, hvis baser er valgt, svarer sammensætningen af ​​lineære kort til matrixmultiplikationen , tilføjelsen af ​​lineære kort svarer til matrixadditionen , og multiplikationen af ​​lineære kort med skalarer svarer til multiplikationen af matricer med skalarer.

Endomorfier og automorfismer

En lineær transformation er en endomorfisme af ; Sættet af alle sådanne endomorfier sammen med addition, sammensætning og skalarmultiplikation som defineret ovenfor danner en associativ algebra med identitetselement over feltet (og især en ring ). Det multiplikative identitetselement i denne algebra er identitetskortet . ${\ textstyle f: V \ til V}$${\ textstyle V}$${\ textstyle \ operatorname {End} (V)}$${\ textstyle K}$ ${\ textstyle \ operatorname {id}: V \ til V}$

En endomorfisme af det er også en isomorfisme kaldes en automorfisme af . Sammensætningen af to automorphisms er igen en automorfi, og sættet af alle automorphisms af danner en gruppe , den automorfi gruppe af er som angivet ved eller . Da automorfismerne netop er de endomorfismer, der besidder inverser under sammensætning, er gruppen af enheder i ringen . ${\ textstyle V}$${\ textstyle V}$${\ textstyle V}$${\ textstyle V}$${\ textstyle \ operatorname {Aut} (V)}$${\ textstyle \ operatorname {GL} (V)}$${\ textstyle \ operatorname {Aut} (V)}$${\ textstyle \ operatorname {End} (V)}$

Hvis den har en endelig dimension , er den isomorf i forhold til den associative algebra for alle matricer med poster i . Automorfismegruppen er isomorf i forhold til den generelle lineære gruppe af alle inverterbare matricer med poster i . ${\ textstyle V}$${\ textstyle n}$${\ textstyle \ operatorname {End} (V)}$${\ tekststil n \ gange n}$${\ textstyle K}$${\ textstyle V}$ ${\ textstyle \ operatorname {GL} (n, K)}$${\ tekststil n \ gange n}$${\ textstyle K}$

Kerne, image og rang -nullitet -sætningen

Hvis er lineær, definerer vi kernen og billedet eller intervallet af by ${\ textstyle f: V \ til W}$${\ textstyle f}$

${\ textstyle \ ker (f)}$er et underrum af og er et underrum af . Følgende dimensionsformel er kendt som rank -nullity -sætningen : ${\ textstyle V}$${\ textstyle \ operatorname {im} (f)}$${\ textstyle W}$

Nummeret kaldes også rang af og skrevet som eller undertiden ,; tallet kaldes nulliteten af og skrevet som eller . Hvis og er endelig-dimensionelle, er baser valgt og repræsenteret ved matricen , så er rangen og nulliteten af ​​henholdsvis matrixens rang og nullitet . ${\ textstyle \ dim (\ operatorname {im} (f))}$${\ textstyle f}$${\ textstyle \ operatorname {rank} (f)}$${\ textstyle \ rho (f)}$${\ textstyle \ dim (\ ker (f))}$${\ textstyle f}$${\ textstyle \ operatorname {null} (f)}$${\ textstyle \ nu (f)}$${\ textstyle V}$${\ textstyle W}$${\ textstyle f}$${\ textstyle A}$${\ textstyle f}$${\ textstyle A}$

Kokernel

En subtil invariant af en lineær transformation er co -kernen , som er defineret som ${\ textstyle f: V \ til W}$

Dette er den dobbelte begreb til kernen: ligesom kernen er en sub rum domæne, co-kerne er en kvotient plads af mål. Formelt har man den nøjagtige sekvens

Disse kan fortolkes således: givet en lineær ligning f ( v ) = w at løse,

• kernen er løsningsrummet til den homogene ligning f ( v ) = 0, og dens dimension er antallet af frihedsgrader i løsningernes rum, hvis den ikke er tom;
• co-kernen er rummet af begrænsninger , som løsningerne skal opfylde, og dens dimension er det maksimale antal uafhængige begrænsninger.

Dimensionen af ​​co-kernen og dimensionen af ​​billedet (rangen) tilføjer op til målrummet. For endelige dimensioner betyder dette, at dimensionen af ​​kvotrummet W / f ( V ) er målrummets dimension minus billedets dimension.

Som et enkelt eksempel kan du overveje kortet f : R ² → R ² , givet ved f ( x , y ) = (0, y ). For at en ligning f ( x , y ) = ( a , b ) skal have en løsning, skal vi have a = 0 (en begrænsning), og i så fald er løsningsrummet ( x , b ) eller tilsvarende angivet, ( 0, b ) + ( x , 0), (en frihedsgrad). Kernen kan udtrykkes som underrummet ( x , 0) < V : værdien af x er friheden i en opløsning - mens cokernel kan udtrykkes via kortet W → R , : givet en vektor ( a , b ), værdien af a er hindringen for, at der er en løsning. ${\ textstyle (a, b) \ mapsto (a)}$

Et eksempel, der illustrerer den uendelige dimensionelle case, er givet ved kortet f : R ^∞ → R ^∞ , med b ₁ = 0 og b _{n + 1} = a _n for n > 0. Dets billede består af alle sekvenser med første element 0, og dermed består dens cokernel af klasser af sekvenser med identisk første element. Selvom dens kerne har dimension 0 (den kortlægger kun nul-sekvensen til nul-sekvensen), har dens co-kerne dimension 1. Da domænet og målrummet er det samme, tilføjes rangen og dimensionen af ​​kernen til den samme sum som rangen og dimensionen af ​​co-kernen ( ), men i det uendelige dimensionelle tilfælde kan det ikke udledes, at kernen og co-kernen af ​​en endomorfisme har den samme dimension (0 ≠ 1). Den omvendte situation opnås for kortet h : R ^∞ → R ^∞ , med c _n = a _{n + 1} . Billedet er hele målrummet, og derfor har dets co-kerne dimension 0, men da den kortlægger alle sekvenser, hvor kun det første element er nul til nul-sekvensen, har dets kerne dimension 1. ${\ textstyle \ left \ {a_ {n} \ right \} \ mapsto \ left \ {b_ {n} \ right \}}$${\ textstyle \ aleph _ {0}+0 = \ aleph _ {0} +1}$${\ textstyle \ left \ {a_ {n} \ right \} \ mapsto \ left \ {c_ {n} \ right \}}$

Indeks

For en lineær operator med endelig-dimensionel kerne og co-kerne kan man definere indeks som:

nemlig frihedsgrader minus antal begrænsninger.

For en transformation mellem endelige-dimensionelle vektorrum er dette kun forskellen dim ( V )-dim ( W ), efter rang-nullitet. Dette giver en indikation af, hvor mange løsninger eller hvor mange begrænsninger man har: Hvis man kortlægger fra et større rum til et mindre, kan kortet være på, og dermed have frihedsgrader, selv uden begrænsninger. Omvendt, hvis kortlægning fra et mindre rum til et større, kan kortet ikke være på, og dermed vil man have begrænsninger selv uden frihedsgrader.

Indekset for en operatør er netop Euler-karakteristikken for 2-termskomplekset 0 → V → W → 0. I operatorteori er indekset for Fredholm-operatører et genstand for undersøgelse, med et stort resultat at Atiyah – Singer-indekssetningen .

Algebraiske klassifikationer af lineære transformationer

Ingen klassificering af lineære kort kunne være udtømmende. Den følgende ufuldstændige liste opregner nogle vigtige klassifikationer, der ikke kræver yderligere struktur på vektorrummet.

Lad V og W betegne vektorrum over et felt F og lad T : V → W være et lineært kort.

Monomorfisme

T siges at være injektiv eller en monomorfisme, hvis en af ​​følgende ækvivalente betingelser er opfyldt:

1. T er en-til-en som et kort over sæt .
2. ker T = {0 _V }
3. dim (ker T ) = 0
4. T er monic eller venstre annulleres, hvilket vil sige, for enhver vektorrum U og helst par af lineære afbildninger R : U → V og S : U → V , ligningen TR = TS indebærer R = S .
5. T er left invertibel , hvilket vil sige at der eksisterer et lineært kort S : W → V , således at ST er identitet kortet på V .

Epimorfisme

T siges at være surjektiv eller en epimorfisme, hvis nogen af ​​følgende ækvivalente betingelser er sande:

1. T er på som et kort over sæt.
2. coker T = {0 _W }
3. T er episk eller højre-annulleres, hvilket vil sige, for enhver vektorrum U og helst par af lineære afbildninger R : W → U og S : W → U , ligningen RT = ST indebærer R = S .
4. T er højre-invertibel , hvilket vil sige at der eksisterer et lineært kort S : W → V , således at TS er identitet kortet på W .

Isomorfisme

T siges at være en isomorfisme, hvis den er både venstre- og højre-invertibel. Dette svarer til, at T er både en-til-en og på (en samling af sæt) eller også, at T er både episk og monisk, og så er en bimorfisme .

Hvis T : V → V er en endomorfisme, så:

• Hvis for et positivt heltal n , n -th iteratet af T , T ⁿ , er identisk nul, så siges T at være nulpotent .
• Hvis T ² = T , så siges T at være idempotent
• Hvis T = kI , hvor k er en eller anden skalar, siges T at være en skaleringstransformation eller skalarmultiplikationskort; se skalarmatrix .

Ændring af grundlag

I betragtning af et lineært kort, som er en endomorfisme, hvis matrix er A , transformerer det i basis B i rummet vektorkoordinater [u] som [v] = A [u]. Når vektorer ændrer sig med inversen af B (vektorer er kontravariant ) er dens inverse transformation [v] = B [v '].

Erstatter dette i det første udtryk

derfor

Derfor er matrixen i det nye grundlag A ′ = B ⁻¹ AB , idet B er matrixen for det givne grundlag.

Derfor siges lineære kort at være 1-co-1-kontra- variantobjekter eller type (1, 1) tensorer .

Kontinuitet

En lineær transformation mellem topologiske vektorrum , f.eks. Normerede rum , kan være kontinuerlig . Hvis dens domæne og codomain er det samme, vil det derefter være en kontinuerlig lineær operator . En lineær operator på et normeret lineært rum er kontinuerlig, hvis og kun hvis den er afgrænset , for eksempel når domænet er endeligt-dimensionelt. Et uendeligt-dimensionelt domæne kan have diskontinuerlige lineære operatorer .

Et eksempel på en ubegrænset, derfor diskontinuerlig, lineær transformation er differentiering på rummet af glatte funktioner udstyret med overordnede norm (en funktion med små værdier kan have et derivat med store værdier, mens derivatet af 0 er 0). For et specifikt eksempel konvergerer sin ( nx )/ n til 0, men dens afledte cos ( nx ) gør det ikke, så differentiering er ikke kontinuerlig ved 0 (og ved en variation af dette argument er den ikke kontinuerlig nogen steder).

Ansøgninger

En specifik anvendelse af lineære kort er til geometriske transformationer, såsom dem, der udføres i computergrafik , hvor oversættelse, rotation og skalering af 2D- eller 3D -objekter udføres ved brug af en transformationsmatrix . Lineære kortlægninger bruges også som en mekanisme til beskrivelse af ændringer: for eksempel i beregning svarer til derivater; eller i relativitet, bruges som en enhed til at holde styr på de lokale transformationer af referencerammer.

En anden anvendelse af disse transformationer er kompileroptimeringer af nested-loop-kode og parallelle kompileringsteknikker .

Se også

• Antilinear kort
• Bøjet funktion
• Afgrænset operatør
• Kontinuerlig lineær operator
• Lineær funktionel
• Lineær isometri

Noter

Bibliografi

• Axler, Sheldon Jay (2015). Lineær algebra udført til højre (3. udgave). Springer . ISBN 978-3-319-11079-0.
• Bronshtein, IN; Semendyayev, KA (2004). Håndbog i matematik (4. udgave). New York: Springer-Verlag. ISBN 3-540-43491-7.
• Halmos, Paul Richard (1974) [1958]. Endelige-dimensionelle vektorrum (2. udgave). Springer . ISBN 0-387-90093-4.
• Horn, Roger A .; Johnson, Charles R. (2013). Matrixanalyse (anden udgave). Cambridge University Press . ISBN 978-0-521-83940-2.
• Katznelson, Yitzhak ; Katznelson, Yonatan R. (2008). A (Terse) Introduktion til lineær algebra . American Mathematical Society . ISBN 978-0-8218-4419-9.
• Lang, Serge (1987), Lineær algebra (tredje udgave), New York: Springer-Verlag , ISBN 0-387-96412-6
• Rudin, Walter (1973). Funktionel analyse . International serie i ren og anvendt matematik. 25 (første udgave). New York, NY: McGraw-Hill Science/Engineering/Math . ISBN 9780070542259.
• Rudin, Walter (1976). Principper for matematisk analyse . Walter Rudin Student Series in Advanced Mathematics (3. udgave). New York: McGraw – Hill. ISBN 978-0-07-054235-8.
• Rudin, Walter (1991). Funktionel analyse . International serie i ren og anvendt matematik. 8 (Anden udgave). New York, NY: McGraw-Hill Science/Engineering/Math . ISBN 978-0-07-054236-5. OCLC  21163277 .
• Schaefer, Helmut H .; Wolff, Manfred P. (1999). Topologiske vektorrum . GTM . 8 (Anden udgave). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC  840278135 .
• Swartz, Charles (1992). En introduktion til funktionsanalyse . New York: M. Dekker. ISBN 978-0-8247-8643-4. OCLC  24909067 .
• Tu, Loring W. (2011). En introduktion til manifolds (2. udgave). Springer . ISBN 978-0-8218-4419-9.
• Wilansky, Albert (2013). Moderne metoder i topologiske vektorrum . Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC  849801114 .