Lineær regression - Linear regression
| Del af en serie om |
| Regressions analyse |
|---|
| Modeller |
| Estimering |
| Baggrund |
I statistik er lineær regression en lineær tilgang til modellering af forholdet mellem en skalær respons og en eller flere forklarende variabler (også kendt som afhængige og uafhængige variabler ). Tilfældet med en forklarende variabel kaldes simpel lineær regression ; for mere end én kaldes processen multipel lineær regression . Dette udtryk adskiller sig fra multivariat lineær regression , hvor flere korrelerede afhængige variabler forudsiges i stedet for en enkelt skalarvariabel.
I lineær regression, er forholdet modelleret ved hjælp lineære prædiktor funktioner hvis ukendt model parametre er estimeret fra data . Sådanne modeller kaldes lineære modeller . Almindeligvis antages det betingede middel af responset givet værdierne af de forklarende variabler (eller forudsigere) at være en affin funktion af disse værdier; mindre almindeligt bruges den betingede median eller en anden kvantil . Ligesom alle former for regressionsanalyse fokuserer lineær regression på responsens betingede sandsynlighedsfordeling givet forudsigernes værdier, snarere end på den fælles sandsynlighedsfordeling for alle disse variabler, som er domænet for multivariat analyse .
Lineær regression var den første type regressionsanalyse, der blev undersøgt grundigt og blev brugt i vid udstrækning i praktiske applikationer. Dette skyldes, at modeller, der afhænger lineært af deres ukendte parametre, er lettere at montere end modeller, der er ikke-lineært relateret til deres parametre, og fordi de statistiske egenskaber for de resulterende estimatorer er lettere at bestemme.
Lineær regression har mange praktiske anvendelser. De fleste applikationer falder ind i en af følgende to brede kategorier:
- Hvis målet er forudsigelse , forudsigelse eller fejlreduktion, kan lineær regression bruges til at tilpasse en forudsigelsesmodel til et observeret datasæt af værdier for responsen og forklarende variabler. Efter at have udviklet en sådan model, hvis yderligere værdier af de forklarende variabler indsamles uden en ledsagende responsværdi, kan den tilpassede model bruges til at forudsige svaret.
- Hvis målet er at forklare variation i responsvariablen, der kan tilskrives variation i de forklarende variabler, kan lineær regressionsanalyse anvendes til at kvantificere styrken af forholdet mellem responsen og de forklarende variabler, og især for at afgøre, om nogle forklarende variabler har muligvis slet ikke noget lineært forhold til svaret eller til at identificere, hvilke undersæt af forklarende variabler der kan indeholde redundante oplysninger om svaret.
Lineære regressionsmodeller monteres ofte ved hjælp af metoden med mindst kvadrater , men de kan også monteres på andre måder, f.eks. Ved at minimere "manglende pasform" i en anden norm (som med mindst absolutte afvigelser regression) eller ved at minimere en straffet version af de mindste kvadraters omkostningsfunktion som i ridge regression ( L 2 -normen straf) og lasso ( L 1 -normen straf). Omvendt kan tilgangen med mindst kvadrater bruges til at passe modeller, der ikke er lineære modeller. Selvom udtrykkene "mindste firkanter" og "lineær model" er tæt forbundet, er de ikke synonyme.
Formulering
Givet et data sæt af n statistiske enheder , en lineær regressionsmodel antager, at forholdet mellem den afhængige variabel y og p -vector af regressorer x er lineær . Dette forhold er modelleret gennem en forstyrrelsesbetegnelse eller fejlvariabel ε - en ikke -observeret tilfældig variabel, der tilføjer "støj" til det lineære forhold mellem den afhængige variabel og regressorer. Således tager modellen form
hvor T betegner transponeringen , så x i T β er det indre produkt mellem vektorer x i og β .
Ofte stables disse n ligninger sammen og skrives i matrixnotation som
hvor
Notation og terminologi
- er en vektor med observerede værdier af variablen kaldet regressand , endogen variabel , responsvariabel , målt variabel , kriterievariabel eller afhængig variabel . Denne variabel er også undertiden kendt som den forudsagte variabel , men dette bør ikke forveksles med forudsagte værdier , som er betegnet . Beslutningen om, hvilken variabel i et datasæt der er modelleret som den afhængige variabel, og som er modelleret som de uafhængige variabler, kan være baseret på en formodning om, at værdien af en af variablerne er forårsaget af eller direkte påvirket af de andre variabler. Alternativt kan der være en operationel grund til at modellere en af variablerne med hensyn til de andre, i hvilket tilfælde der ikke behøver at være nogen formodning om kausalitet.
-
kan ses som en matrix af rækkevektorer eller af n -dimensionale søjlevektorer , der er kendt som regressorer , eksogene variabler , forklarende variabler , kovariater , inputvariabler , forudsigelsesvariabler eller uafhængige variabler (må ikke forveksles med begrebet af uafhængige tilfældige variabler ). Matricen kaldes undertiden designmatrixen .
- Normalt er en konstant inkluderet som en af regressorerne. Især for . Det tilsvarende element i
- Nogle gange kan en af regressorerne være en ikke-lineær funktion af en anden regressor eller af dataene, som ved polynomisk regression og segmenteret regression . Modellen forbliver lineær, så længe den er lineær i parametervektoren β .
- Værdierne x ij kan betragtes som enten observerede værdier for tilfældige variabler X j eller som faste værdier valgt før observering af den afhængige variabel. Begge fortolkninger kan være passende i forskellige tilfælde, og de fører generelt til de samme estimeringsprocedurer; dog bruges forskellige tilgange til asymptotisk analyse i disse to situationer.
Tilpasning af en lineær model til et givet datasæt kræver normalt en estimering af regressionskoefficienterne, således at fejlbegrebet minimeres. For eksempel er det almindeligt at bruge summen af kvadrerede fejl som et mål for minimering.
Eksempel
Overvej en situation, hvor en lille kugle bliver kastet op i luften, og derefter måler vi dens højde for opstigning h i på forskellige tidspunkter t i . Fysik fortæller os, at hvis man ignorerer trækket, kan forholdet modelleres som
hvor β 1 bestemmer boldens starthastighed, β 2 er proportional med standardtyngdekraften , og ε i skyldes målefejl. Lineær regression kan bruges til at estimere værdierne for β 1 og β 2 ud fra de målte data. Denne model er ikke-lineær i tidsvariablen, men den er lineær i parametrene β 1 og β 2 ; hvis vi tager regressorer x i = ( x i 1 , x i 2 ) = ( t i , t i 2 ), tager modellen standardformen
Antagelser
Standard lineære regressionsmodeller med standardestimeringsteknikker gør et antal antagelser om forudsigelsesvariablerne, responsvariablerne og deres forhold. Der er udviklet utallige udvidelser, der gør det muligt at lempe hver af disse antagelser (dvs. reducere til en svagere form) og i nogle tilfælde eliminere helt. Generelt gør disse udvidelser estimeringsproceduren mere kompleks og tidskrævende og kan også kræve flere data for at producere en lige præcis model.
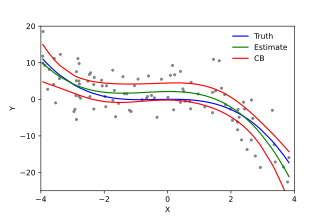
Følgende er de vigtigste antagelser fra standard lineære regressionsmodeller med standardestimeringsteknikker (f.eks. Almindelige mindste kvadrater ):
- Svag eksogenitet . Dette betyder i det væsentlige, at forudsigelsesvariablerne x kan behandles som faste værdier, snarere end tilfældige variabler . Det betyder f.eks., At forudsigelsesvariablerne antages at være fejlfrie-det vil sige ikke forurenet med målefejl. Selvom denne antagelse ikke er realistisk i mange indstillinger, fører det til betydeligt vanskeligere modeller med fejl-i-variabler ved at droppe den .
- Linearitet . Det betyder, at middelværdien af responsvariablen er en lineær kombination af parametrene (regressionskoefficienter) og forudsigelsesvariablerne. Bemærk, at denne antagelse er meget mindre restriktiv, end den umiddelbart kan synes. Fordi forudsigelsesvariablerne behandles som faste værdier (se ovenfor), er linearitet egentlig kun en begrænsning af parametrene. Selve forudsigelsesvariablerne kan transformeres vilkårligt, og faktisk kan flere kopier af den samme underliggende forudsigelsesvariabel tilføjes, hver enkelt transformeres forskelligt. Denne teknik bruges f.eks. I polynomisk regression , som bruger lineær regression til at passe responsvariablen som en vilkårlig polynomfunktion (op til en given rang) af en forudsigelsesvariabel. Med denne store fleksibilitet har modeller som polynomisk regression ofte "for meget magt", idet de har en tendens til at overmontere dataene. Som følge heraf skal der typisk bruges en form for regulering for at forhindre, at urimelige løsninger kommer ud af estimeringsprocessen. Almindelige eksempler er højderygregression og lassoregression . Bayesisk lineær regression kan også bruges, som i sin natur er mere eller mindre immun over for problemet med overmontering. (Faktisk kan rygregression og lasso -regression begge ses som særlige tilfælde af Bayesiansk lineær regression, med bestemte typer tidligere fordelinger placeret på regressionskoefficienterne.)
- Konstant varians (alias homoscedasticitet ). Det betyder, at variansen af fejlene ikke afhænger af værdierne i forudsigelsesvariablerne. Således er variabiliteten af svarene for givne faste værdier af forudsigerne den samme, uanset hvor store eller små svarene er. Dette er ofte ikke tilfældet, da en variabel, hvis gennemsnit er stor, typisk vil have en større varians end en, hvis middel er lille. For eksempel kan en person, hvis indkomst forventes at være $ 100.000 $ let have en faktisk indkomst på $ 80.000 eller $ 120.000 - det vil sige en standardafvigelse på omkring $ 20.000 - mens en anden person med en forudsagt indkomst på $ 10.000 sandsynligvis ikke vil have den samme $ 20.000 standardafvigelse , da det ville betyde, at deres faktiske indkomst kan variere alt mellem $ 10.000 og $ 30.000. (Faktisk, som dette viser, i mange tilfælde - ofte de samme tilfælde, hvor antagelsen om normalfordelte fejl fejler - bør variansen eller standardafvigelsen forudsiges at være proportional med middelværdien, snarere end konstant.) Fraværet af homoscedasticitet er kaldes heteroscedasticitet . For at kontrollere denne antagelse kan et plot af rester versus forudsagte værdier (eller værdierne for hver enkelt forudsigelse) undersøges for en "blæsende effekt" (dvs. stigende eller faldende lodret spredning, når man bevæger sig fra venstre mod højre på plottet) . Et plot af de absolutte eller kvadratiske rester versus de forudsagte værdier (eller hver forudsigelse) kan også undersøges for en tendens eller krumning. Formelle tests kan også bruges; se heteroscedasticitet . Tilstedeværelsen af heteroscedasticitet vil resultere i, at et generelt "gennemsnitligt" estimat af varians bruges i stedet for et, der tager højde for den sande variansstruktur. Dette fører til mindre præcise (men i tilfælde af almindelige mindst kvadrater , ikke forudindtaget) parameterestimater og forudindtagede standardfejl, hvilket resulterer i vildledende test og intervalestimater. Den gennemsnitlige kvadratiske fejl for modellen vil også være forkert. Forskellige estimeringsteknikker, herunder vægtede mindst kvadrater og brug af heteroscedasticitet-konsistente standardfejl, kan håndtere heteroscedasticitet på en ganske generel måde. Bayesiske lineære regressionsteknikker kan også bruges, når variansen antages at være en funktion af middelværdien. Det er også muligt i nogle tilfælde at løse problemet ved at anvende en transformation på responsvariablen (f.eks. Tilpasning af responsvariabelens logaritme ved hjælp af en lineær regressionsmodel, hvilket indebærer, at responsvariablen selv har en log-normalfordeling i stedet for en normal fordeling ).
-
Uafhængighed af fejl . Dette forudsætter, at fejlvariablerne i responsvariablerne ikke er korreleret med hinanden. (Faktisk statistisk uafhængighed er en stærkere betingelse end blot mangel på korrelation og er ofte ikke nødvendig, selvom det kan udnyttes, hvis det er kendt at holde.) Nogle metoder, såsom generaliserede mindste firkanter, er i stand til at håndtere korrelerede fejl, selvom de typisk kræver betydeligt flere data, medmindre en form for regulering bruges til at skæve modellen mod antagelse af ukorrelerede fejl. Bayesisk lineær regression er en generel måde at håndtere dette problem på.
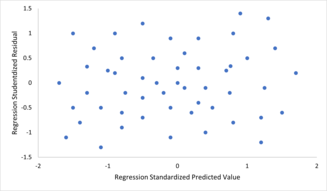 For at kontrollere for krænkelser af forudsætningerne om linearitet, konstant varians og uafhængighed af fejl inden for en lineær regressionsmodel afbildes resterne typisk mod de forudsagte værdier (eller hver af de individuelle forudsigere). En tilsyneladende tilfældig spredning af punkter om den vandrette midterlinje ved 0 er ideel, men kan ikke udelukke visse former for overtrædelser, såsom autokorrelation i fejlene eller deres korrelation med en eller flere kovariater.
For at kontrollere for krænkelser af forudsætningerne om linearitet, konstant varians og uafhængighed af fejl inden for en lineær regressionsmodel afbildes resterne typisk mod de forudsagte værdier (eller hver af de individuelle forudsigere). En tilsyneladende tilfældig spredning af punkter om den vandrette midterlinje ved 0 er ideel, men kan ikke udelukke visse former for overtrædelser, såsom autokorrelation i fejlene eller deres korrelation med en eller flere kovariater. - Manglende perfekt multicollinearitet i forudsigerne. For standardmetoder til estimering af mindste kvadrater skal designmatrixen X have fuld kolonnerangering p ; ellers eksisterer perfekt multikollinearitet i forudsigelsesvariablerne, hvilket betyder, at der eksisterer et lineært forhold mellem to eller flere forudsigelsesvariabler. Dette kan skyldes uheld ved at kopiere en variabel i dataene ved hjælp af en lineær transformation af en variabel sammen med originalen (f.eks. De samme temperaturmålinger udtrykt i Fahrenheit og Celsius) eller ved at inkludere en lineær kombination af flere variabler i modellen, såsom deres gennemsnit. Det kan også ske, hvis der er for få data til rådighed i forhold til antallet af parametre, der skal estimeres (f.eks. Færre datapunkter end regressionskoefficienter). Nær overtrædelser af denne antagelse, hvor forudsigere er stærkt, men ikke perfekt korreleret, kan reducere præcisionen af parameterestimater (se Variationsinflationsfaktor ). I tilfælde af perfekt multicollinearity vil parametervektoren β være ikke-identificerbar-den har ingen unik løsning. I et sådant tilfælde kun nogle af parametrene kan identificeres (dvs. deres værdier kan kun skønnes inden nogle lineær underrum af den fulde parameter space R p ). Se delvis mindste kvadraters regression . Metoder til tilpasning af lineære modeller med multicollinearity er blevet udviklet, hvoraf nogle kræver yderligere antagelser som "effekt sparsitet" - at en stor brøkdel af effekterne er nøjagtigt nul. Bemærk, at de mere beregningsmæssigt dyre itererede algoritmer til parameterestimering, såsom dem, der bruges i generaliserede lineære modeller , ikke lider af dette problem.
Ud over disse antagelser påvirker flere andre statistiske egenskaber af dataene stærkt forskellige estimeringsmetoders ydeevne:
- Det statistiske forhold mellem fejlbetingelserne og regressorerne spiller en vigtig rolle for at afgøre, om en estimeringsprocedure har ønskelige prøveudtagningsegenskaber, såsom at være upartisk og konsekvent.
- Arrangementet eller sandsynlighedsfordelingen af forudsigelsesvariablerne x har stor indflydelse på præcisionen af estimater af β . Prøveudtagning og design af eksperimenter er højt udviklede underfelter af statistikker, der giver vejledning til indsamling af data på en sådan måde at opnå et præcist estimat af β .
Fortolkning

En monteret lineær regressionsmodel kan bruges til at identificere forholdet mellem en enkelt forudsigelsesvariabel x j og responsvariablen y, når alle de andre forudsigelsesvariabler i modellen "holdes faste". Konkret er fortolkningen af β j den forventede ændring i y for en enhedsændring i x j, når de andre kovariater holdes faste-det vil sige den forventede værdi af det partielle derivat af y med hensyn til x j . Dette kaldes undertiden den unikke effekt af x j på y . I modsætning hertil kan den marginale effekt af x j på y vurderes ved hjælp af en korrelationskoefficient eller simpel lineær regressionsmodel , der kun vedrører x j til y ; denne effekt er det totale derivat af y med hensyn til x j .
Der skal udvises forsigtighed ved fortolkning af regressionsresultater, da nogle af regressorerne muligvis ikke tillader marginale ændringer (f.eks. Dummy -variabler eller aflytningsterm), mens andre ikke kan holdes fast (husk eksemplet fra indledningen: det ville være umuligt at "holde t i fast" og samtidig ændre værdien af t i 2 ).
Det er muligt, at den unikke effekt kan være næsten nul, selv når den marginale effekt er stor. Dette kan betyde, at en anden kovariat fanger alle oplysninger i x j , så når variablen først er i modellen, er der ikke noget bidrag fra x j til variationen i y . Omvendt kan den unikke effekt af x j være stor, mens dens marginale effekt er næsten nul. Dette ville ske, hvis de andre kovariater forklarede meget af variationen af y , men de forklarer hovedsageligt variationen på en måde, der er komplementær til det, der fanges af x j . I dette tilfælde reducerer inkluderingen af de andre variabler i modellen den del af variabiliteten af y , der ikke er relateret til x j , og styrker derved det tilsyneladende forhold til x j .
Betydningen af udtrykket "fastholdt" kan afhænge af, hvordan værdierne i forudsigelsesvariablerne opstår. Hvis eksperimentatoren direkte angiver værdierne for forudsigelsesvariablerne i henhold til et undersøgelsesdesign, kan sammenligningerne af interesse bogstaveligt talt svare til sammenligninger mellem enheder, hvis forudsigelsesvariabler er blevet "holdt fast" af eksperimentatoren. Alternativt kan udtrykket "fastholdt" referere til et udvalg, der finder sted i forbindelse med dataanalyse. I dette tilfælde "holder vi en variabel fast" ved at begrænse vores opmærksomhed på de undersæt af dataene, der tilfældigvis har en fælles værdi for den givne forudsigelsesvariabel. Dette er den eneste fortolkning af "fastholdt", der kan bruges i en observationsundersøgelse.
Forestillingen om en "unik effekt" er tiltalende, når man studerer et komplekst system, hvor flere indbyrdes forbundne komponenter påvirker responsvariablen. I nogle tilfælde kan det bogstaveligt talt tolkes som årsagseffekten af en intervention, der er knyttet til værdien af en forudsigelsesvariabel. Det er imidlertid blevet argumenteret for, at multiple regressionsanalyser i mange tilfælde ikke klarer at afklare forholdet mellem forudsigelsesvariablerne og responsvariablen, når forudsigelserne er korreleret med hinanden og ikke tildeles efter et undersøgelsesdesign.
Udvidelser
Talrige forlængelser af lineær regression er blevet udviklet, som gør det muligt at lempe nogle eller alle de forudsætninger, der ligger til grund for basismodellen.
Enkel og multipel lineær regression

Den meget enkle tilfælde af en enkelt skalar prædiktor variabel x og en enkelt skalar responsvariabel y er kendt som simpel lineær regression . Udvidelsen til flere og / eller vektor -valued prediktorvariabler (betegnet med et stort X ) er kendt som multipel lineær regression , også kendt som multivariabel lineær regression (ikke at forveksle med multivariabel lineær regression ).
Multipel lineær regression er en generalisering af simpel lineær regression i tilfælde af mere end en uafhængig variabel og et specielt tilfælde af generelle lineære modeller, begrænset til en afhængig variabel. Grundmodellen for multipel lineær regression er
for hver observation i = 1, ..., n .
I formlen ovenfor betragter vi n observationer af en afhængig variabel og p uafhængige variabler. Således, Y i er i th observation af den afhængige variabel, X ij er i th observation af j th uafhængige variabel, j = 1, 2, ..., s . Værdierne p j repræsenterer parametre, der skal estimeres, og Ea jeg er i th uafhængige identisk fordelte normal fejl.
I den mere generelle multivariate lineære regression er der en ligning af ovenstående form for hver af m > 1 afhængige variabler, der deler det samme sæt forklarende variabler og derfor estimeres samtidigt med hinanden:
for alle observationer indekseret som i = 1, ..., n og for alle afhængige variabler indekseret som j = 1, ..., m .
Næsten alle virkelige regressionsmodeller involverer flere forudsigere, og grundlæggende beskrivelser af lineær regression er ofte formuleret i form af multipel regressionsmodel. Bemærk dog, at responsvariablen y i disse tilfælde stadig er en skalar. Et andet udtryk, multivariat lineær regression , refererer til tilfælde, hvor y er en vektor, dvs. det samme som generel lineær regression .
Generelle lineære modeller
Den generelle lineære model overvejer situationen, når responsvariablen ikke er en skalar (for hver observation), men en vektor, y i . Betinget linearitet forudsættes stadig, idet en matrix B erstatter vektoren β i den klassiske lineære regressionsmodel. Multivariate analoger af almindelige mindste kvadrater (OLS) og generaliserede mindste kvadrater (GLS) er blevet udviklet. "Generelle lineære modeller" kaldes også "multivariate lineære modeller". Disse er ikke det samme som multivariable lineære modeller (også kaldet "multiple lineære modeller").
Heteroscedastiske modeller
Der er skabt forskellige modeller, der tillader heteroscedasticitet , dvs. fejlene for forskellige responsvariabler kan have forskellige afvigelser . For eksempel er vægtede mindste kvadrater en metode til at estimere lineære regressionsmodeller, når responsvariablerne kan have forskellige fejlvariationer, muligvis med korrelerede fejl. (Se også Vægtede lineære mindste kvadrater og Generaliserede mindste kvadrater .) Heteroscedasticitetskonsistente standardfejl er en forbedret metode til brug med ukorrelerede, men potentielt heteroscedastiske fejl.
Generaliserede lineære modeller
Generaliserede lineære modeller (GLM'er) er en ramme for modellering af responsvariabler, der er afgrænsede eller diskrete. Dette bruges f.eks.
- ved modellering af positive mængder (f.eks. priser eller populationer), der varierer i stor skala-som er bedre beskrevet ved hjælp af en skæv fordeling, f.eks. log-normalfordelingen eller Poisson-distributionen (selvom GLM'er ikke bruges til log-normale data, i stedet svaret variabel transformeres ganske enkelt ved hjælp af logaritmefunktionen);
- ved modellering af kategoriske data , såsom valg af en given kandidat ved et valg (hvilket er bedre beskrevet ved hjælp af en Bernoulli-fordeling / binomial distribution til binære valg, eller en kategorisk fordeling / multinomial fordeling til flervejsvalg), hvor der er en fast antal valg, der ikke kan ordnes meningsfuldt;
- ved modellering af ordinære data , f.eks. vurderinger på en skala fra 0 til 5, hvor de forskellige resultater kan ordnes, men hvor mængden i sig selv muligvis ikke har nogen absolut betydning (f.eks. kan en vurdering på 4 ikke være "dobbelt så god" i noget mål forstand som en vurdering på 2, men angiver ganske enkelt, at det er bedre end 2 eller 3, men ikke så godt som 5).
Generaliserede lineære modeller giver mulighed for en vilkårlig link funktion , g , som relaterer middelværdien af responsvariabel (erne) til prædiktorer: . Linkfunktionen er ofte relateret til fordelingen af responset, og især har den typisk virkningen af at transformere mellem den lineære forudsigelses rækkevidde og responsvariabelens område.
Nogle almindelige eksempler på GLM'er er:
- Poisson -regression for tælledata.
- Logistisk regression og probit regression for binære data.
- Multinomial logistisk regression og multinomial probit -regression for kategoriske data.
- Bestilte logit og beordrede probit -regression for ordinære data.
Enkeltindeksmodeller tillader en vis grad af ulinearitet i forholdet mellem x og y , samtidig med at den lineære forudsigelses β ′ x centrale rolle bevares som i den klassiske lineære regressionsmodel. Under visse betingelser vil ganske enkelt at anvende OLS til data fra en enkeltindeks-model konsekvent estimere β op til en proportionalitetskonstant.
Hierarkiske lineære modeller
Hierarkiske lineære modeller (eller flere regression ) organiserer data i et hierarki af regressioner, for eksempel, hvor A er svandt på B , og B er svandt på C . Det bruges ofte, hvor variablerne af interesse har en naturlig hierarkisk struktur, såsom i uddannelsesstatistik, hvor eleverne er indlejret i klasseværelser, klasseværelser er indlejret i skoler, og skoler er indlejret i en eller anden administrativ gruppering, såsom et skoledistrikt. Svarvariablen kan være et mål for elevernes præstationer, f.eks. En testscore, og forskellige kovariater vil blive indsamlet på klasse-, skole- og skoledistriktniveauer.
Fejl-i-variabler
Fejl-i-variabler-modeller (eller "målefejlmodeller") udvider den traditionelle lineære regressionsmodel, så forudsigelsesvariablerne X kan observeres med fejl. Denne fejl får standardestimatorer for β til at blive forudindtaget. Generelt er formen af bias en dæmpning, hvilket betyder, at virkningerne er forudindstillet mod nul.
Andre
- I Dempster-Shafer teori , eller en lineær tro funktion kan især en lineær regressionsmodel repræsenteres som en delvis fejet matrix, som kan kombineres med lignende matricer repræsenterer observationer og andre antagne normale fordelinger og tilstandsligninger. Kombinationen af fejede eller ikke -fejede matricer giver en alternativ metode til at estimere lineære regressionsmodeller.
Estimeringsmetoder
Et stort antal procedurer er blevet udviklet til parameterestimering og inferens i lineær regression. Disse metoder adskiller sig i beregningsmæssig enkelhed af algoritmer, tilstedeværelse af en løsning med lukket form, robusthed med hensyn til kraftige fordelinger og teoretiske antagelser, der er nødvendige for at validere ønskelige statistiske egenskaber såsom konsistens og asymptotisk effektivitet .
Nogle af de mere almindelige estimeringsteknikker til lineær regression er opsummeret nedenfor.
Forudsat at den uafhængige variabel er og modellens parametre er , så ville modellens forudsigelse være
- .
Hvis forlænges til derefter ville blive et prikprodukt af parameteren og den uafhængige variabel, dvs.
- .
I indstillingen med mindst kvadrater er den optimale parameter defineret som sådan, der minimerer summen af gennemsnitligt kvadrat tab:
Når man nu sætter de uafhængige og afhængige variabler i henholdsvis matricer og tab, kan tabsfunktionen omskrives som:
Da tabet er konveks, ligger den optimale løsning ved gradientnul. Gradienten af tabsfunktionen er (ved hjælp af nævnerlayoutkonvention ):
Indstilling af gradienten til nul giver den optimale parameter:
Bemærk: For at bevise, at det opnåede faktisk er det lokale minimum, skal man igen differentiere for at få den hessiske matrix og vise, at det er positivt bestemt. Dette leveres af Gauss -Markov -sætningen .
Lineære mindste kvadrater metoder omfatter hovedsageligt:
- Maksimal sandsynlighedsestimering kan udføres, når fordelingen af fejltermerne vides at tilhøre en bestemt parametrisk familie ƒ θ af sandsynlighedsfordelinger . Når f θ er en normalfordeling med nul middelværdi og varians θ, er det resulterende skøn identisk med OLS -estimatet. GLS -estimater er maksimale sandsynlighedsestimater, når ε følger en multivariat normalfordeling med en kendt kovariansmatrix .
- Ridge -regression og andre former for straffet estimering, såsom Lasso -regression , introducerer bevidst bias i estimeringen af β for at reducereestimatets variabilitet . De resulterende skøn har generelt lavere gennemsnitlige kvadratfejl end OLS -estimaterne, især når multicollinearitet er til stede, eller når overmontering er et problem. De bruges generelt, når målet er at forudsige værdien af responsvariablen y for værdier af forudsigerne x, der endnu ikke er blevet observeret. Disse metoder er ikke så almindeligt anvendte, når målet er slutning, da det er svært at tage højde for bias.
- Mindst absolut afvigelse (LAD) regression er en robust estimeringsteknik ved, at den er mindre følsom over for tilstedeværelsen af outliers end OLS (men er mindre effektiv end OLS, når der ikke er nogen outliers). Det svarer til maksimal sandsynlighedsestimering under en Laplace -fordelingsmodel for ε .
- Adaptiv estimering . Hvis vi antager, at fejltermer er uafhængige af regressorerne, så er den optimale estimator 2-trins MLE, hvor det første trin bruges til ikke-parametrisk at estimere fordelingen af fejlbegrebet.
Andre estimeringsteknikker

- Bayesisk lineær regression anvender rammen for bayesisk statistik til lineær regression. (Se også Bayesiansk multivariat lineær regression .) Især regressionskoefficienterne β antages at være tilfældige variabler med en specificeret forudgående fordeling . Den tidligere fordeling kan forspænde løsningerne for regressionskoefficienterne på en måde, der ligner (men mere generel end) kamregression eller lasso -regression . Derudover producerer den bayesiske estimeringsproces ikke et enkelt punktestimat for regressionskoefficienternes "bedste" værdier, men en hel posterior fordeling , der fuldstændig beskriver usikkerheden omkring mængden. Dette kan bruges til at estimere de "bedste" koefficienter ved hjælp af middelværdien, tilstanden, medianen, enhver kvantil (se kvantil regression ) eller en hvilken som helst anden funktion af den bageste fordeling.
- Fraktil regression fokuserer på de betingede fraktiler af y givet X snarere end den betingede gennemsnit af y givet X . Lineær kvantil regression modellerer en bestemt betinget kvantil, for eksempel den betingede median, som en lineær funktion β T x af forudsigerne.
- Blandede modeller bruges i vid udstrækning til at analysere lineære regressionsforhold, der involverer afhængige data, når afhængighederne har en kendt struktur. Almindelige anvendelser af blandede modeller omfatter analyse af data, der involverer gentagne målinger, såsom langsgående data eller data opnået fra klyngeudtagning. De passer generelt som parametriske modeller ved hjælp af maksimal sandsynlighed eller Bayesiansk estimering. I det tilfælde, hvor fejlene er modelleret som normale tilfældige variabler, er der en tæt forbindelse mellem blandede modeller og generaliserede mindst kvadrater. Estimering af faste effekter er en alternativ tilgang til analyse af denne type data.
- Hovedkomponentregression (PCR) bruges, når antallet af forudsigelsesvariabler er stort, eller når der er stærke korrelationer mellem forudsigelsesvariablerne. Denne totrinsprocedure reducerer først forudsigelsesvariablerne ved hjælp af hovedkomponentanalyse og bruger derefter de reducerede variabler i en OLS-regressionspasning. Selvom det ofte fungerer godt i praksis, er der ingen generel teoretisk grund til, at den mest informative lineære funktion af forudsigelsesvariablerne skal ligge blandt de dominerende hovedkomponenter i multivariatfordelingen af forudsigelsesvariablerne. Den delvise mindste kvadraters regression er forlængelsen af PCR -metoden, som ikke lider af den nævnte mangel.
- Mindste vinkelregression er en estimeringsprocedure for lineære regressionsmodeller, der blev udviklet til at håndtere højdimensionelle kovariatvektorer, muligvis med flere kovariater end observationer.
- Den Theil-Sen estimator er en simpel robust estimering teknik, der vælger hældningen af fit-linie for at være medianen af skråningerne af linjer gennem parrene af prøvepunkter. Det har lignende statistiske effektivitetsegenskaber til simpel lineær regression, men er meget mindre følsom over for udliggere .
- Andre robuste estimeringsteknikker, herunder den α-trimmede middelmetode , og L-, M-, S- og R-estimatorer er blevet introduceret.
Ansøgninger
Lineær regression bruges i vid udstrækning inden for biologiske, adfærdsmæssige og sociale videnskaber til at beskrive mulige sammenhænge mellem variabler. Det er et af de vigtigste værktøjer, der bruges i disse discipliner.
Trend linje
En trendlinje repræsenterer en trend, den langsigtede bevægelse i tidsseriedata efter at der er taget højde for andre komponenter. Det fortæller, om et bestemt datasæt (f.eks. BNP, oliepriser eller aktiekurser) er steget eller faldet over den periode. En trendlinje kunne simpelthen trækkes med øjet gennem et sæt datapunkter, men mere korrekt beregnes deres position og hældning ved hjælp af statistiske teknikker som lineær regression. Trendlinjer er typisk lige linjer, selvom nogle variationer bruger polynom i højere grad afhængigt af den ønskede krumningsgrad i linjen.
Trendlinjer bruges undertiden i virksomhedsanalyser til at vise ændringer i data over tid. Dette har fordelen ved at være enkelt. Trendlinjer bruges ofte til at argumentere for, at en bestemt handling eller begivenhed (såsom træning eller en reklamekampagne) forårsagede observerede ændringer på et tidspunkt. Dette er en simpel teknik og kræver ikke en kontrolgruppe, eksperimentelt design eller en sofistikeret analyseteknik. Det lider imidlertid af mangel på videnskabelig validitet i tilfælde, hvor andre potentielle ændringer kan påvirke dataene.
Epidemiologi
Tidlige beviser vedrørende tobaksrygning til dødelighed og sygelighed kom fra observationsstudier, der anvendte regressionsanalyse. For at reducere falske korrelationer ved analyse af observationsdata inkluderer forskere normalt flere variabler i deres regressionsmodeller ud over variablen af primær interesse. For eksempel i en regressionsmodel, hvor cigaretrygning er den uafhængige variabel af primær interesse, og den afhængige variabel er levetid målt i år, kan forskere inkludere uddannelse og indkomst som yderligere uafhængige variabler for at sikre, at enhver observeret effekt af rygning på levetiden er ikke på grund af de andre socioøkonomiske faktorer . Det er imidlertid aldrig muligt at inkludere alle mulige forvirrende variabler i en empirisk analyse. For eksempel kan et hypotetisk gen øge dødeligheden og også få folk til at ryge mere. Af denne grund er randomiserede kontrollerede forsøg ofte i stand til at generere mere overbevisende beviser for årsagssammenhænge, end der kan opnås ved hjælp af regressionsanalyser af observationsdata. Når kontrollerede eksperimenter ikke er mulige, kan varianter af regressionsanalyse såsom instrumentale variabler regression bruges til at forsøge at estimere årsagssammenhænge ud fra observationsdata.
Finansiere
Den model Capital Asset Pricing bruger lineær regression samt begrebet beta til at analysere og kvantificere den systematiske risiko ved en investering. Dette kommer direkte fra beta -koefficienten for den lineære regressionsmodel, der relaterer investeringsafkastet til afkastet af alle risikable aktiver.
Økonomi
Lineær regression er det dominerende empiriske værktøj inden for økonomi . For eksempel bruges det til at forudsige forbrugsudgifter , faste investeringsudgifter , lagerinvesteringer , indkøb af et lands eksport , udgifter til import , efterspørgslen efter at beholde likvide aktiver , efterspørgsel efter arbejdskraft og arbejdsudbud .
Miljøvidenskab
Lineær regression finder anvendelse i en lang række miljøvidenskabelige applikationer. I Canada bruger Environmental Effects Monitoring Program statistiske analyser af fisk og bentiske undersøgelser til at måle virkningerne af papirmasse- eller metalmineaffald på det akvatiske økosystem.
Maskinelæring
Lineær regression spiller en vigtig rolle i underfeltet for kunstig intelligens kendt som maskinlæring . Den lineære regressionsalgoritme er en af de grundlæggende overvågede maskinlæringsalgoritmer på grund af dens relative enkelhed og velkendte egenskaber.
Historie
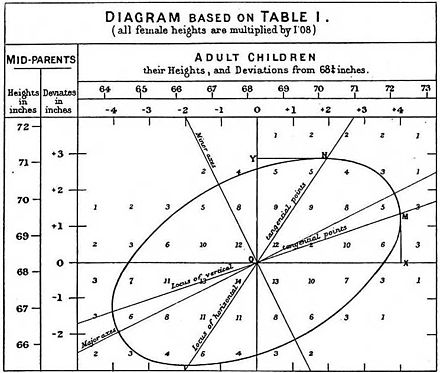
Mindste kvadrater lineær regression, som et middel til at finde en god ru lineær tilpasning til et sæt punkter blev udført af Legendre (1805) og Gauss (1809) til forudsigelse af planetarisk bevægelse. Quetelet var ansvarlig for at gøre proceduren kendt og for at bruge den i vid udstrækning inden for samfundsvidenskab.
Se også
- Variansanalyse
- Blinder – Oaxaca nedbrydning
- Censureret regressionsmodel
- Tværsnitsregression
- Kurvetilpasning
- Empiriske Bayes -metoder
- Fejl og restværdier
- Manglende pasformssum af kvadrater
- Linjefitting
- Lineær klassifikator
- Lineær ligning
- Logistisk regression
- M-estimator
- Multivariat adaptiv regression splines
- Ikke -lineær regression
- Ikke -parametrisk regression
- Normale ligninger
- Projektionsjagtregression
- Responsmodelleringsmetode
- Segmenteret lineær regression
- Trinvis regression
- Strukturel pause
- Support vektor maskine
- Afkortet regressionsmodel
- Deming regression
Referencer
Citater
Kilder
- Cohen, J., Cohen P., West, SG, & Aiken, LS (2003). Anvendt multiple regressions-/korrelationsanalyser for adfærdsvidenskaberne . (2. udgave) Hillsdale, NJ: Lawrence Erlbaum Associates
- Charles Darwin . Variationen af dyr og planter under domesticering . (1868) (Kapitel XIII beskriver, hvad man vidste om reversering på Galtons tid. Darwin bruger udtrykket "reversion".)
- Draper, NR; Smith, H. (1998). Anvendt regressionsanalyse (3. udgave). John Wiley. ISBN 978-0-471-17082-2.
- Francis Galton. "Regression mod middelmådighed i arvelig statur," Journal of the Anthropological Institute , 15: 246-263 (1886). (Telefax på: [1] )
- Robert S. Pindyck og Daniel L. Rubinfeld (1998, 4t red.). Econometriske modeller og økonomiske prognoser , kap. 1 (Intro, inkl. Bilag om Σ operatorer & afledning af parameterest.) & Bilag 4.3 (mult. Regression i matrixform).
Yderligere læsning
- Pedhazur, Elazar J (1982). Multiple regression i adfærdsforskning: Forklaring og forudsigelse (2. udgave). New York: Holt, Rinehart og Winston. ISBN 978-0-03-041760-3.
- Mathieu Rouaud, 2013: Sandsynlighed, statistik og estimering Kapitel 2: Lineær regression, lineær regression med fejlstænger og ikke -lineær regression.
- National Physical Laboratory (1961). "Kapitel 1: Lineære ligninger og matricer: Direkte metoder". Moderne computermetoder . Noter om anvendt videnskab. 16 (2. udgave). Hendes Majestæts brevpapir .
eksterne links
- Mindste kvadraters regression , PhET interaktive simuleringer, University of Colorado at Boulder
- DIY lineær pasform






























![{\ displaystyle {\ vec {x_ {i}}} = \ venstre [x_ {1}^{i}, x_ {2}^{i}, \ ldots, x_ {m}^{i} \ højre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/156ecace8a311d501c63ca49c73bba6efc915283)
![{\ displaystyle {\ vec {\ beta}} = \ venstre [\ beta _ {0}, \ beta _ {1}, \ ldots, \ beta _ {m} \ højre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32434f0942d63c868f23d5af39442bb90783633b)


![{\ displaystyle {\ vec {x_ {i}}} = \ venstre [1, x_ {1}^{i}, x_ {2}^{i}, \ ldots, x_ {m}^{i} \ højre ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f72fa7acd1682497c285884b0686d784d8b0eb15)








