Lorenz-system - Lorenz system

Ikke forveksles med Lorenz-kurve eller Lorentz-distribution .
En prøveopløsning i Lorenz-tiltrækkeren, når ρ = 28, σ = 10 og β = 8/3

Den Lorenz-systemet er et system af ordinære differentialligninger først undersøgt af Edward Lorenz . Det er bemærkelsesværdigt for at have kaotiske løsninger til bestemte parameterværdier og indledende betingelser. Især Lorenz-tiltrækkeren er et sæt kaotiske løsninger i Lorenz-systemet. I populære medier stammer " sommerfugleffekten " fra virkeligheden af ​​Lorenz-tiltrækkeren, dvs. vores vinger), vil vores evne til at forudsige dets fremtidige kurs altid mislykkes. Dette understreger, at fysiske systemer kan være helt deterministiske og alligevel stadig være uforudsigelige, selv i fravær af kvanteeffekter. Formen på selve Lorenz-tiltrækkeren, når den er tegnet grafisk, kan også ses som en sommerfugl.

Oversigt

I 1963 udviklede Edward Lorenz med hjælp fra Ellen Fetter en forenklet matematisk model til atmosfærisk konvektion . Modellen er et system med tre almindelige differentialligninger, nu kendt som Lorenz-ligningerne:

Ligningerne vedrører egenskaberne af et todimensionelt væskelag, der er opvarmet ensartet nedenfra og afkølet ovenfra. Især beskriver ligningerne hastigheden for ændring af tre størrelser med hensyn til tid: er proportional med konvektionshastigheden, den vandrette temperaturvariation og den lodrette temperaturvariation. Konstanterne , og er systemparametre, der er proportionale med Prandtl-nummeret , Rayleigh-nummeret og visse fysiske dimensioner af selve laget.

Lorenz-ligningerne opstår også i forenklede modeller til lasere , dynamoer , termosyphoner , børsteløse jævnstrømsmotorer , elektriske kredsløb , kemiske reaktioner og fremad osmose . Lorenz-ligningerne er også de styrende ligninger i Fourier-rummet for Malkus-vandhjulet . Malkus vandhjul udviser kaotisk bevægelse, i stedet for at dreje i en retning med konstant hastighed, vil dets rotation fremskynde, bremse, stoppe, ændre retninger og svinge frem og tilbage mellem kombinationer af sådan adfærd på en uforudsigelig måde.

Fra et teknisk synspunkt er Lorenz-systemet ikke- lineært , ikke-periodisk, tredimensionelt og deterministisk . Lorenz-ligningerne har været genstand for hundredvis af forskningsartikler og mindst en undersøgelse af boglængden.

Analyse

Et normalt antager, at parametrene , og er positive. Lorenz brugte værdierne , og . Systemet udviser kaotisk adfærd for disse (og nærliggende) værdier.

Hvis der så kun er ét ligevægtspunkt, som er ved oprindelsen. Dette punkt svarer til ingen konvektion. Alle baner konvergerer til oprindelsen, som er en global tiltrækker , når .

En bifkorking af gaffel forekommer ved , og for yderligere to kritiske punkter vises ved: og Disse svarer til konstant konvektion. Dette par af ligevægtspunkter er kun stabilt, hvis

som kun kan holde for positive hvis . Ved den kritiske værdi mister begge ligevægtspunkter stabilitet gennem en subkritisk Hopf-bifurkation .

Når , og , har Lorenz-systemet kaotiske løsninger (men ikke alle løsninger er kaotiske). Næsten alle indledende punkter har tendens til at være et invariant sæt - Lorenz-tiltrækkeren - en mærkelig tiltrækker , en fraktal og en selvopspændt tiltrækker med hensyn til alle tre ligevægte. Dens Hausdorff-dimension estimeres ovenfra af Lyapunov-dimensionen (Kaplan-Yorke-dimensionen) til 2,06 ± 0,01, og korrelationsdimensionen estimeres til at være 2,05 ± 0,01. Den nøjagtige Lyapunov-formel for den globale tiltrækning kan findes analytisk under klassiske begrænsninger for parametrene:

Lorenz-tiltrækkeren er vanskelig at analysere, men virkningen af ​​differentialligningen på tiltrækkeren er beskrevet af en ret simpel geometrisk model. Bevis for, at dette faktisk er tilfældet, er det fjortende problem på listen over Smales problemer . Dette problem var det første, der blev løst af Warwick Tucker i 2002.

For andre værdier af viser systemet knyttede periodiske baner. For eksempel bliver den en T (3,2) torusknude .

Eksempel på løsninger til Lorenz-systemet til forskellige værdier af ρ
Lorenz Ro14 20 41 20-200px.png Lorenz Ro13-200px.png
ρ = 14, σ = 10, β = 8/3 (Forstør) ρ = 13, σ = 10, β = 8/3 (Forstør)
Lorenz Ro15-200px.png Lorenz Ro28-200px.png
ρ = 15, σ = 10, β = 8/3 (Forstør) ρ = 28, σ = 10, β = 8/3 (Forstør)
For små værdier på ρ er systemet stabilt og udvikler sig til en af ​​to fastpunkttraktorer. Når ρ er større end 24,74, bliver de faste punkter frastødende, og banen afvises af dem på en meget kompleks måde.
Følsom afhængighed af den oprindelige tilstand
Tid t = 1 (Forstør) Tid t = 2 (Forstør) Tid t = 3 (Forstør)
Lorenz caos1-175.png Lorenz caos2-175.png Lorenz caos3-175.png
Disse tal - lavet ved hjælp af ρ = 28, σ = 10 og β = 8/3 - viser tre tidssegmenter af 3D-udviklingen af ​​to baner (den ene i blå, den anden i gul) i Lorenz-tiltrækkeren, der starter ved to indledende punkter, der kun adskiller sig med 10 −5 i x- koordinaten. Oprindeligt synes de to baner at være sammenfaldende (kun den gule kan ses, da den er trukket over den blå), men efter nogen tid er forskellen tydelig.

Forbindelse til teltkort

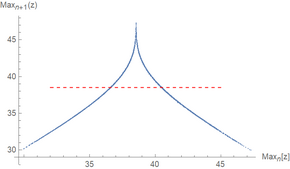
En rekreation af Lorenz's resultater skabt på Mathematica . Punkter over den røde linje svarer til systemets skiftende lapper.

I figur 4 i sit papir afbildede Lorenz den relative maksimale værdi i z-retningen opnået af systemet mod det tidligere relative maksimum i z-retningen. Denne procedure blev senere kendt som et Lorenz-kort (ikke at forveksle med et Poincaré-plot , som tegner krydset mellem en bane med en foreskrevet overflade). Det resulterende plot har en form, der minder meget om teltkortet . Lorenz fandt også, at når den maksimale z-værdi er over en bestemt afskæring, skifter systemet til den næste lap. Ved at kombinere dette med det kaos, der vides at være udstillet af teltkortet, viste han, at systemet skifter kaotisk mellem de to lapper.

Simuleringer

MATLAB-simulering

% Solve over time interval [0,100] with initial conditions [1,1,1]
% ''f'' is set of differential equations
% ''a'' is array containing x, y, and z variables
% ''t'' is time variable

sigma = 10;
beta = 8/3;
rho = 28;
f = @(t,a) [-sigma*a(1) + sigma*a(2); rho*a(1) - a(2) - a(1)*a(3); -beta*a(3) + a(1)*a(2)];
[t,a] = ode45(f,[0 100],[1 1 1]);     % Runge-Kutta 4th/5th order ODE solver
plot3(a(:,1),a(:,2),a(:,3))

Mathematica simulation

Standard måde: 

tend = 50;
eq = {x'[t] == σ (y[t] - x[t]), 
      y'[t] == x[t] (ρ - z[t]) - y[t], 
      z'[t] == x[t] y[t] - β z[t]};
init = {x[0] == 10, y[0] == 10, z[0] == 10};
pars = {σ->10, ρ->28, β->8/3};
{xs, ys, zs} = 
  NDSolveValue[{eq /. pars, init}, {x, y, z}, {t, 0, tend}];
ParametricPlot3D[{xs[t], ys[t], zs[t]}, {t, 0, tend}]

Mindre detaljeret: 

lorenz = NonlinearStateSpaceModel[{{σ (y - x), x (ρ - z) - y, x y - β z}, {}}, {x, y, z}, {σ, ρ, β}];
soln[t_] = StateResponse[{lorenz, {10, 10, 10}}, {10, 28, 8/3}, {t, 0, 50}];
ParametricPlot3D[soln[t], {t, 0, 50}]

Python-simulering

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D

rho = 28.0
sigma = 10.0
beta = 8.0 / 3.0

def f(state, t):
    x, y, z = state  # Unpack the state vector
    return sigma * (y - x), x * (rho - z) - y, x * y - beta * z  # Derivatives

state0 = [1.0, 1.0, 1.0]
t = np.arange(0.0, 40.0, 0.01)

states = odeint(f, state0, t)

fig = plt.figure()
ax = fig.gca(projection="3d")
ax.plot(states[:, 0], states[:, 1], states[:, 2])
plt.draw()
plt.show()

Afledning af Lorenz-ligningerne som model for atmosfærisk konvektion

Lorenz-ligningerne stammer fra Oberbeck – Boussinesq-tilnærmelsen til ligningerne, der beskriver væskecirkulation i et lavt lag af væske, opvarmet ensartet nedenfra og afkølet ensartet ovenfra. Denne væskecirkulation er kendt som Rayleigh-Bénard-konvektion . Væsken antages at cirkulere i to dimensioner (lodret og vandret) med periodiske rektangulære randbetingelser.

De delvise differentialligninger, der modellerer systemets strømfunktion og temperatur, udsættes for en spektral Galerkin-tilnærmelse : De hydrodynamiske felter udvides i Fourier-serier, der derefter afkortes kraftigt til et enkelt udtryk for strømfunktionen og to udtryk for temperaturen. Dette reducerer modelligningerne til et sæt af tre koblede, ikke-lineære almindelige differentialligninger. En detaljeret afledning kan for eksempel findes i ikke-lineære dynamiske tekster. Lorenz-systemet er en reduceret version af et større system, der tidligere blev undersøgt af Barry Saltzman.

Løsning af Smales 14. problem

Smales 14. problem siger 'Udviser egenskaberne til Lorenz-tiltrækkeren det for en mærkelig tiltrækker ?', Blev det besvaret bekræftende af Warwick Tucker i 2002. For at bevise dette resultat brugte Tucker strenge numeriske metoder som intervalregning og normale former . For det første definerede Tucker et tværsnit , der skæres på tværs af strømningsbanerne. Ud fra dette kan man definere kortet for første retur , som tildeler hver det punkt, hvor banen for første skærer hinanden .

Derefter opdeles beviset i tre hovedpunkter, der bevises og antyder eksistensen af ​​en mærkelig tiltrækker. De tre punkter er:

  • Der findes en region, der er uforanderlig under kortet med første retur, hvilket betyder
  • Returkortet tillader et fremad invariant keglefelt
  • Vektorer inde i dette invariante keglefelt udvides ensartet med afledningen af returkortet.

For at bevise det første punkt bemærker vi, at tværsnittet er skåret af to buer dannet af (se). Tucker dækker placeringen af ​​disse to buer med små rektangler , hvilket foreningen af ​​disse rektangler giver . Nu er målet at bevise, at for alle punkter ind , vil strømmen bringe punkterne tilbage ind . For at gøre det tager vi en plan nedenfor på en lille afstand , så ved at tage centrum af og bruge Euler-integrationsmetoden kan man estimere, hvor strømmen bringer ind, hvilket giver os et nyt punkt . Derefter kan man estimere, hvor punkterne i vil blive kortlagt ved hjælp af Taylor-ekspansion, dette giver os et nyt rektangel centreret på . Således ved vi, at alle punkter i vil blive kortlagt . Målet er at gøre denne metode rekursivt, indtil strømmen kommer tilbage til, og vi får et rektangel i sådan, at vi ved det . Problemet er, at vores skøn kan blive upræcis efter flere iterationer, og det, hvad Tucker gør, er at opdele i mindre rektangler og derefter anvende processen rekursivt. Et andet problem er, at når vi anvender denne algoritme, bliver strømmen mere 'vandret' (se), hvilket fører til en dramatisk stigning i upræcision. For at forhindre dette ændrer algoritmen tværsnitsretningen og bliver enten vandret eller lodret.

Bidrag

Lorenz anerkender bidragene fra Ellen Fetter i sin artikel, som er ansvarlig for de numeriske simuleringer og figurer. Også, Margaret Hamilton hjulpet i de indledende, numeriske beregninger, der fører op til resultaterne af Lorenz-modellen.

Galleri

  • En løsning i Lorenz-tiltrækkeren afbildet med høj opløsning i xz-planet.

  • En løsning i Lorenz-tiltrækkeren gengivet som en SVG.

  • En animation, der viser baner med flere løsninger i et Lorenz-system.

  • En løsning i Lorenz-tiltrækkeren gengivet som en metaltråd til at vise retning og 3D- struktur.

  • En animation, der viser forskellen på nærliggende løsninger til Lorenz-systemet.

  • En visualisering af Lorenz-tiltrækkeren nær en periodisk cyklus.

  • To strømlinjer i et Lorenz-system, fra rho = 0 til rho = 28 (sigma = 10, beta = 8/3)

  • Animation af et Lorenz-system med rhoafhængighed

Se også

Bemærkninger

Referencer

Yderligere læsning

eksterne links