Matematik -Mathematics

Matematik
Ren Fundamenter Analyse Algebra Talteori Kombinatorik Geometri Topologi Anvendt Sandsynlighed Statistikker Beregningsvidenskab Matematisk fysik Operationsforskning Matematisk optimering Beregningsbiologi Beregningslingvistik
Artikler
0-9 EN B C D E F G H jeg J K L M N O P Q R S T U V W x Y Z
Videnskabsmænd
EN B C D E F G H jeg J K L M N O P Q R S T U V W x Y Z
Navigation
Lister Omrids Portal Områder
v t e

3. århundrede f.Kr. græsk matematiker Euklid (holder skydemåtter ), som forestillet af Rafael i denne detalje fra The School of Athens (1509-1511)

Matematik (fra oldgræsk μάθημα ( máthēma )  'viden, undersøgelse, læring') er et vidensområde, som omfatter studiet af emner som tal ( aritmetik og talteori ), formler og relaterede strukturer ( algebra ), former og rum hvori de er indeholdt ( geometri ), og mængder og deres ændringer ( kalkulus og analyse ). Der er ingen generel konsensus om dets nøjagtige omfang eller epistemologiske status .

Det meste af matematisk aktivitet består i at opdage og bevise (ved ren ræsonnement) egenskaber ved abstrakte objekter . Disse objekter er enten abstraktioner fra naturen (såsom naturlige tal eller linjer ), eller (i moderne matematik) abstrakte enheder, af hvilke visse egenskaber, kaldet aksiomer , er fastsat. Et bevis består af en række anvendelser af nogle deduktive regler til allerede kendte resultater, herunder tidligere beviste sætninger , aksiomer og (i tilfælde af abstraktion fra naturen) nogle grundlæggende egenskaber, der betragtes som sande udgangspunkter for den undersøgte teori. Resultatet af et bevis kaldes en sætning .

Matematik er meget brugt i videnskaben til modellering af fænomener. Dette muliggør udvinding af kvantitative forudsigelser fra eksperimentelle love. For eksempel kan planeternes bevægelse forudsiges med høj nøjagtighed ved hjælp af Newtons tyngdelov kombineret med matematisk beregning. Den matematiske sandheds uafhængighed af enhver eksperimentering indebærer, at nøjagtigheden af ​​sådanne forudsigelser kun afhænger af modellens tilstrækkelighed til at beskrive virkeligheden. Så når der opstår nogle unøjagtige forudsigelser, betyder det, at modellen skal forbedres eller ændres, ikke at matematikken er forkert. For eksempel kan perihelionpræcessionen af ​​Merkur ikke forklares af Newtons tyngdelov, men forklares nøjagtigt af Einsteins generelle relativitetsteori . Denne eksperimentelle validering af Einsteins teori viser, at Newtons tyngdelov kun er en tilnærmelse (som stadig er meget nøjagtig i hverdagen).

Matematik er afgørende på mange områder, herunder naturvidenskab , ingeniørvidenskab , medicin , finans , datalogi og samfundsvidenskab . Nogle områder af matematik, såsom statistik og spilteori , er udviklet i direkte sammenhæng med deres anvendelser og er ofte grupperet under navnet anvendt matematik . Andre matematiske områder udvikles uafhængigt af enhver applikation (og kaldes derfor ren matematik ), men praktiske applikationer opdages ofte senere. Et passende eksempel er problemet med heltalsfaktorisering , som går tilbage til Euclid , men som ikke havde nogen praktisk anvendelse før dens brug i RSA-kryptosystemet (til sikkerhed for computernetværk ).

Matematik har været en menneskelig aktivitet lige så langt tilbage, som der findes skriftlige optegnelser . Men begrebet "bevis" og dets tilhørende " matematiske stringens " dukkede først op i græsk matematik , især i Euklids elementer . Matematik udviklede sig i et relativt langsomt tempo indtil renæssancen , hvor algebra og infinitesimalregning blev tilføjet til aritmetik og geometri som hovedområder i matematikken. Siden da har samspillet mellem matematiske innovationer og videnskabelige opdagelser ført til en hurtig stigning i antallet af matematiske opdagelser. I slutningen af ​​det 19. århundrede førte matematikkens grundlæggende krise til systematiseringen af ​​den aksiomatiske metode . Dette gav igen anledning til en dramatisk stigning i antallet af matematikområder og deres anvendelsesområder; et vidne til dette er Mathematics Subject Classification , som oplister mere end tres første-niveau områder af matematik.

Matematikområder

Før renæssancen blev matematik opdelt i to hovedområder: aritmetik , der var afsat til manipulation af tal , og geometri , der var viet til studiet af former. Der var også nogle pseudovidenskab , såsom numerologi og astrologi , der ikke var klart adskilt fra matematik.

Omkring renæssancen dukkede to nye hovedområder op. Indførelsen af ​​matematisk notation førte til algebra , som groft sagt består af undersøgelse og manipulation af formler . Calculus , en forkortelse af infinitesimalregning og integralregning , er studiet af kontinuerte funktioner , som modellerer ændringen af ​​og forholdet mellem varierende størrelser ( variable ). Denne opdeling i fire hovedområder forblev gyldig indtil slutningen af ​​det 19. århundrede, selvom nogle områder, såsom himmelmekanik og fast mekanik , som ofte blev betragtet som matematik, nu anses for at høre til fysikken . Også nogle fag udviklet i denne periode går forud for matematik (der er opdelt i forskellige) områder, såsom sandsynlighedsteori og kombinatorik , som først senere blev betragtet som selvstændige områder.

I slutningen af ​​det 19. århundrede førte den grundlæggende krise i matematikken og den deraf følgende systematisering af den aksiomatiske metode til en eksplosion i mængden af ​​matematikkens områder. Matematikfagsklassifikationen indeholder mere end 60 førsteniveauområder . Nogle af disse områder svarer til den ældre opdeling i fire hovedområder. Dette er tilfældet med talteori (det moderne navn for højere aritmetik ) og geometri . Der er dog flere andre områder på første niveau, der har "geometri" i deres navn eller almindeligvis anses for at høre til geometri. Algebra og calculus optræder ikke som områder på første niveau, men er hver opdelt i flere områder på første niveau. Andre områder på første niveau eksisterede slet ikke før det 20. århundrede (f.eks. kategoriteori ; homologisk algebra og datalogi ) eller blev ikke tidligere betragtet som matematik, såsom 03: Matematisk logik og grundlag (herunder modelteori , beregnelighedsteori , mængdelære , bevisteori og algebraisk logik ).

Talteori

Fordelingen af ​​primtal er et centralt studiepunkt i talteorien. Denne Ulam-spiral tjener til at illustrere det, idet den især antyder den betingede uafhængighed mellem at være primtal og at være en værdi af visse kvadratiske polynomier.

Talteori startede med manipulation af tal , det vil sige naturlige tal, og blev senere udvidet til heltal og rationelle tal Talteori blev tidligere kaldt aritmetik , men i dag bruges dette udtryk mest til beregningsmetoderne med tal. ${\displaystyle (\mathbb {N} ),}$ ${\displaystyle (\mathbb {Z} )}$ ${\displaystyle (\mathbb {Q} ).}$

En specificitet ved talteori er, at mange problemer, der kan angives meget elementært, er meget vanskelige, og når de er løst, har de en løsning, der kræver meget sofistikerede metoder, der kommer fra forskellige dele af matematikken. Et bemærkelsesværdigt eksempel er Fermats sidste sætning , der blev fremsat i 1637 af Pierre de Fermat og først bevist i 1994 af Andrew Wiles , ved at bruge blandt andet algebraisk geometri (mere specifikt skemateori ), kategoriteori og homologisk algebra . Et andet eksempel er Goldbachs formodning , der hævder, at hvert lige heltal større end 2 er summen af ​​to primtal . Udtalt i 1742 af Christian Goldbach er det stadig ubevist på trods af betydelig indsats.

I lyset af mangfoldigheden af ​​de undersøgte problemer og løsningsmetoderne er talteori i øjeblikket opdelt i flere underområder, som omfatter analytisk talteori , algebraisk talteori , talgeometri (metodeorienteret), diofantiske ligninger og transcendens teori (problemorienteret) .

Geometri

Geometri er, med aritmetik , en af ​​de ældste grene af matematik. Det startede med empiriske opskrifter vedrørende former, såsom linjer , vinkler og cirkler , som hovedsageligt blev udviklet til behov for opmåling og arkitektur .

En grundlæggende nyskabelse var udarbejdelsen af ​​beviser af de gamle grækere : det er ikke tilstrækkeligt at verificere ved måling, at f.eks. to længder er lige store. En sådan egenskab skal bevises ved abstrakt ræsonnement fra tidligere beviste resultater ( sætninger ) og grundlæggende egenskaber (som betragtes som selvindlysende, fordi de er for grundlæggende til at være genstand for et bevis ( postulater )). Dette princip, som er grundlæggende for al matematik, blev udarbejdet for geometriens skyld og blev systematiseret af Euklid omkring 300 f.Kr. i sin bog Elementer .

Den resulterende euklidiske geometri er studiet af former og deres arrangementer konstrueret ud fra linjer , planer og cirkler i det euklidiske plan ( plan geometri ) og det (tredimensionelle) euklidiske rum .

Euklidisk geometri blev udviklet uden ændring af metoder eller omfang indtil det 17. århundrede, hvor René Descartes introducerede det, der nu kaldes kartesiske koordinater . Dette var en stor paradigmeændring, da det i stedet for at definere reelle tal som længder af linjestykker (se tallinje ), tillod repræsentationen af ​​punkter ved hjælp af tal (deres koordinater) og til brug af algebra og senere, calculus til løsning geometriske problemer. Denne opdelte geometri i to dele, der kun adskiller sig ved deres metoder, syntetisk geometri , som bruger rene geometriske metoder, og analytisk geometri , som bruger koordinater systemisk.

Analytisk geometri tillader studiet af nye former, især kurver , der ikke er relateret til cirkler og linjer; disse kurver defineres enten som grafer over funktioner (hvis undersøgelse førte til differentialgeometri ), eller ved implicitte ligninger , ofte polynomielle ligninger (som affødte algebraisk geometri ). Analytisk geometri gør det muligt at betragte rums dimensioner højere end tre (det er tilstrækkeligt at overveje mere end tre koordinater), som ikke længere er en model af det fysiske rum.

Geometri udvidede sig hurtigt i løbet af det 19. århundrede. En stor begivenhed var opdagelsen (i anden halvdel af det 19. århundrede) af ikke-euklidiske geometrier , som er geometrier, hvor det parallelle postulat er opgivet. Dette er, udover Russels paradoks , et af udgangspunkterne for matematikkens grundlæggende krise , ved at sætte spørgsmålstegn ved sandheden af ​​det førnævnte postulat. Dette aspekt af krisen blev løst ved at systematisere den aksiomatiske metode og vedtage, at sandheden af ​​de valgte aksiomer ikke er et matematisk problem. Til gengæld giver den aksiomatiske metode mulighed for at studere forskellige geometrier opnået enten ved at ændre aksiomerne eller ved at overveje egenskaber, der er invariante under specifikke transformationer af rummet . Dette resulterer i en række underområder og generaliseringer af geometri, der inkluderer:

• Projektiv geometri , introduceret i det 16. århundrede af Girard Desargues , udvider den euklidiske geometri ved at tilføje punkter i det uendelige , hvor parallelle linjer skærer hinanden. Dette forenkler mange aspekter af klassisk geometri ved at undgå at have en anderledes behandling for krydsende og parallelle linjer.
• Affin geometri , studiet af egenskaber i forhold til parallelitet og uafhængig af længdebegrebet.
• Differentialgeometri , studiet af kurver, overflader og deres generaliseringer, som defineres ved hjælp af differentiable funktioner
• Manifold teori , studiet af former, der ikke nødvendigvis er indlejret i et større rum
• Riemannsk geometri , studiet af afstandsegenskaber i buede rum
• Algebraisk geometri , studiet af kurver, overflader og deres generaliseringer, som defineres ved hjælp af polynomier
• Topologi , studiet af egenskaber, der holdes under kontinuerlige deformationer
  • Algebraisk topologi , anvendelse i topologi af algebraiske metoder, hovedsageligt homologisk algebra
• Diskret geometri , studiet af endelige konfigurationer i geometri
• Konveks geometri , studiet af konvekse sæt , som tager sin betydning fra sine applikationer til optimering
• Kompleks geometri , geometrien opnået ved at erstatte reelle tal med komplekse tal

Algebra

Algebra kan ses som kunsten at manipulere ligninger og formler . Diophantus (3. århundrede) og Al-Khwarizmi (9. århundrede) var to hovedforløbere for algebra. Den første løste nogle relationer mellem ukendte naturlige tal (det vil sige ligninger) ved at udlede nye relationer, indtil man fik løsningen. Den anden introducerede systematiske metoder til at transformere ligninger (såsom at flytte et led fra en side af en ligning til den anden side). Udtrykket algebra er afledt af det arabiske ord, som han brugte til at navngive en af ​​disse metoder i titlen på hans hovedafhandling .

Den andengradsformel udtrykker kortfattet løsningerne af alle andengradsligninger

Algebra begyndte kun at være et specifikt område med François Viète (1540-1603), som introducerede brugen af ​​bogstaver ( variabler ) til at repræsentere ukendte eller uspecificerede tal. Dette gør det muligt kortfattet at beskrive de operationer , der skal udføres på tallene repræsenteret af variablerne.

Indtil det 19. århundrede bestod algebra hovedsageligt af studiet af lineære ligninger , der kaldes i øjeblikket lineær algebra , og polynomieligninger i en enkelt ukendt , som blev kaldt algebraiske ligninger (et udtryk, der stadig er i brug, selvom det kan være tvetydigt). I løbet af det 19. århundrede begyndte variabler at repræsentere andre ting end tal (såsom matricer , modulære heltal og geometriske transformationer ), som nogle operationer kan fungere på, som ofte er generaliseringer af aritmetiske operationer. For at håndtere dette blev begrebet algebraisk struktur introduceret, som består af et sæt, hvis elementer er uspecificerede, af operationer, der virker på elementerne i sættet, og regler, som disse operationer skal følge. Så omfanget af algebra udviklede sig til i det væsentlige at blive studiet af algebraiske strukturer. Dette algebraobjekt blev kaldt moderne algebra eller abstrakt algebra , det sidstnævnte udtryk bliver stadig brugt, hovedsageligt i en pædagogisk kontekst, i modsætning til elementær algebra , som handler om den ældre måde at manipulere formler på.

Rubiks terning: studiet af dens mulige bevægelser er en konkret anvendelse af gruppeteori

Nogle typer algebraiske strukturer har egenskaber, der er nyttige og ofte grundlæggende inden for mange områder af matematikken. Deres undersøgelse er i dag autonome dele af algebra, som omfatter:

• gruppeteori ;
• feltteori ;
• vektorrum , hvis undersøgelse i det væsentlige er det samme som lineær algebra ;
• ringteori ;
• kommutativ algebra , som er studiet af kommutative ringe , omfatter studiet af polynomier og er en grundlæggende del af algebraisk geometri ;
• homologisk algebra
• Lie algebra og Lie gruppe teori;
• Boolsk algebra , som er meget udbredt til undersøgelse af computeres logiske struktur .

Studiet af typer algebraiske strukturer som matematiske objekter er genstand for universel algebra og kategoriteori . Sidstnævnte gælder for enhver matematisk struktur (ikke kun de algebraiske). Ved sin oprindelse blev det introduceret sammen med homologisk algebra for at tillade algebraisk undersøgelse af ikke-algebraiske objekter såsom topologiske rum ; dette særlige anvendelsesområde kaldes algebraisk topologi .

Kalkulation og analyse

Calculus, tidligere kaldet infinitesimal calculus , blev introduceret i det 17. århundrede af Newton og Leibniz , uafhængigt og samtidigt. Det er grundlæggende studiet af forholdet mellem to skiftende størrelser, kaldet variable , sådan at den ene afhænger af den anden. Calculus blev stort set udvidet i det 18. århundrede af Euler , med introduktionen af ​​begrebet en funktion , og mange andre resultater. I øjeblikket refererer "calculus" hovedsageligt til den elementære del af denne teori, og "analyse" bruges almindeligvis til avancerede dele.

Analyse er yderligere underopdelt i reel analyse , hvor variabler repræsenterer reelle tal og kompleks analyse, hvor variabler repræsenterer komplekse tal . I øjeblikket er der mange underområder af analyse, nogle deles med andre områder af matematik; De omfatter:

• Multivariabel beregning
• Funktionel analyse , hvor variable repræsenterer varierende funktioner;
• Integration , måleteori og potentialteori , alle stærkt forbundet med sandsynlighedsteori ;
• Almindelige differentialligninger ;
• Partielle differentialligninger ;
• Numerisk analyse , hovedsageligt afsat til beregning på computere af løsninger af almindelige og partielle differentialligninger, der opstår i mange anvendelser af matematik.

Diskret matematik

Matematisk logik og mængdelære

Disse fag hører til matematik siden slutningen af ​​det 19. århundrede. Før denne periode blev mængder ikke betragtet som matematiske objekter , og logik , selvom det blev brugt til matematiske beviser , tilhørte filosofien og blev ikke specifikt studeret af matematikere.

Før studiet af uendelige mængder af Georg Cantor , matematikere var tilbageholdende med at overveje samlinger , der faktisk er uendelige , og betragtes uendelig som et resultat af en endeløs opregning . Cantors arbejde stødte mange matematikere ikke kun ved at overveje faktisk uendelige mængder, men også ved at vise, at dette indebærer forskellige størrelser af uendelighed (se Cantors diagonale argument ) og eksistensen af ​​matematiske objekter, der ikke kan beregnes, og ikke engang kan beskrives eksplicit (f.eks. , Hamel baser af de reelle tal over de rationelle tal ). Dette førte til kontroversen om Cantors mængdeteori .

I samme periode viste det sig på forskellige områder af matematikken, at de tidligere intuitive definitioner af de grundlæggende matematiske objekter var utilstrækkelige til at sikre matematisk stringens . Eksempler på sådanne intuitive definitioner er "et sæt er en samling af objekter", " naturligt tal er det, der bruges til at tælle", "et punkt er en form med en længde på nul i hver retning", "en kurve er et spor efterladt af et bevægende punkt", osv.

Dette er oprindelsen til matematikkens grundlæggende krise . Det er til sidst blevet løst i matematikkens mainstream ved at systematisere den aksiomatiske metode i en formaliseret mængdeteori . Groft sagt er hvert matematisk objekt defineret af mængden af ​​alle lignende objekter og de egenskaber, som disse objekter skal have. For eksempel, i Peano aritmetik , er de naturlige tal defineret af "nul er et tal", "hvert tal som en unik efterfølger", "hvert tal men nul har en unik forgænger" og nogle ræsonnementsregler. "Karten" af de objekter, der er defineret på denne måde, er et filosofisk problem, som matematikere overlader til filosoffer, selvom mange matematikere har meninger om denne natur, og bruger deres mening - nogle gange kaldet "intuition" - til at lede deres undersøgelse og finde beviser.

Denne tilgang gør det muligt at betragte "logikker" (det vil sige sæt tilladte udledningsregler), sætninger , beviser osv. som matematiske objekter og at bevise sætninger om dem. For eksempel hævder Gödels ufuldstændighedssætninger groft sagt, at der i enhver teori, der indeholder de naturlige tal, er sætninger, der er sande (det kan bevises i en større teori), men som ikke kan bevises inde i teorien.

Denne tilgang til grundlaget for matematikken blev udfordret i den første halvdel af det 20. århundrede af matematikere ledet af LEJ Brouwer , der fremmede en intuitionistisk logik , der udelukker loven om udelukket mellem .

Disse problemer og debatter førte til en bred udvidelse af matematisk logik, med delområder som modelteori (modellering af nogle logiske teorier inden for anden teori), bevisteori , typeteori , beregningsbarhedsteori og beregningskompleksitetsteori . Selvom disse aspekter af matematisk logik blev introduceret før fremkomsten af ​​computere , bidrog deres brug i compilerdesign , programcertificering , korrekturassistenter og andre aspekter af datalogi til udvidelsen af ​​disse logiske teorier.

Anvendt matematik

Anvendt matematik beskæftiger sig med matematiske metoder, der typisk bruges i naturvidenskab, ingeniørvidenskab , erhvervsliv og industri . Således er "anvendt matematik" en matematisk videnskab med specialiseret viden . Begrebet anvendt matematik beskriver også det faglige speciale, hvor matematikere arbejder med praktiske problemer; som en profession fokuseret på praktiske problemer, fokuserer anvendt matematik på "formulering, undersøgelse og brug af matematiske modeller" inden for videnskab, teknik og andre områder af matematisk praksis.

Tidligere har praktiske anvendelser motiveret udviklingen af ​​matematiske teorier, som så blev genstand for studier i ren matematik, hvor matematik udvikles primært for sin egen skyld. Aktiviteten af ​​anvendt matematik er således afgørende forbundet med forskning i ren matematik .

Statistik og andre beslutningsvidenskaber

Anvendt matematik har betydeligt overlap med disciplinen statistik, hvis teori er formuleret matematisk, især med sandsynlighedsteori . Statistikere (der arbejder som en del af et forskningsprojekt) "skaber data, der giver mening" med tilfældige stikprøver og med randomiserede eksperimenter ; designet af en statistisk prøve eller et eksperiment specificerer analysen af ​​dataene (før dataene bliver tilgængelige). Når man genovervejer data fra eksperimenter og prøver eller når man analyserer data fra observationsstudier , "gør statistikere mening om dataene" ved hjælp af modelleringskunsten og inferens - teorien - med modelvalg og estimering ; de estimerede modeller og konsekvente forudsigelser bør testes på nye data .

Statistisk teori studerer beslutningsproblemer såsom at minimere risikoen ( forventet tab ) af en statistisk handling, såsom at bruge en procedure i for eksempel parameterestimering , hypotesetestning og udvælgelse af den bedste . I disse traditionelle områder af matematisk statistik formuleres et statistisk beslutningsproblem ved at minimere en objektiv funktion , såsom forventet tab eller omkostning , under specifikke begrænsninger: For eksempel involverer design af en undersøgelse ofte at minimere omkostningerne ved at estimere et befolkningsgennemsnit med en given niveau af tillid. På grund af sin brug af optimering deler den matematiske teori om statistik bekymringer med andre beslutningsvidenskaber , såsom operationsforskning , kontrolteori og matematisk økonomi .

Beregningsmatematik

Beregningsmatematik foreslår og studerer metoder til løsning af matematiske problemer , der typisk er for store til den menneskelige numeriske kapacitet. Numerisk analyse studerer metoder til problemstillinger i analyse ved hjælp af funktionel analyse og tilnærmelsesteori ; numerisk analyse omfatter bredt studiet af tilnærmelse og diskretisering med særligt fokus på afrundingsfejl . Numerisk analyse og mere generelt videnskabelig databehandling studerer også ikke-analytiske emner inden for matematisk videnskab, især algoritmisk - matrix- og - grafteori . Andre områder af beregningsmatematik omfatter computeralgebra og symbolsk beregning .

Spilteori	Væskedynamik	Numerisk analyse	Optimering	Sandsynlighedsteori	Statistikker	Kryptografi
Matematisk økonomi	Matematisk fysik	Matematisk kemi	Matematisk biologi	Matematisk økonomi	Kontrolteori

Historie

Matematikkens historie kan ses som en stadigt stigende række af abstraktioner . Evolutionært set var den første abstraktion, der nogensinde fandt sted, som deles af mange dyr, formentlig tal: erkendelsen af, at en samling af to æbler og en samling af to appelsiner (for eksempel) har noget til fælles, nemlig mængden af deres medlemmer. Som det fremgår af opgørelser fundet på knogler, kan forhistoriske mennesker ud over at genkende, hvordan man tæller fysiske objekter, også have erkendt, hvordan man tæller abstrakte mængder, såsom tid - dage, årstider eller år.

Den babylonske matematiske tavle Plimpton 322, dateret til 1800 f.Kr.

Beviser for mere kompleks matematik dukker ikke op før omkring 3000  f.Kr. , hvor babylonierne og egypterne begyndte at bruge aritmetik , algebra og geometri til beskatning og andre økonomiske beregninger, til bygning og konstruktion og til astronomi . De ældste matematiske tekster fra Mesopotamien og Egypten er fra 2000 til 1800 f.Kr. Mange tidlige tekster nævner Pythagoras tripler , og derfor synes Pythagoras sætning at være det ældste og mest udbredte matematiske koncept efter grundlæggende aritmetik og geometri. Det er i babylonsk matematik , at elementær aritmetik ( addition , subtraktion , multiplikation og division ) først optræder i den arkæologiske optegnelse. Babylonierne besad også et stedværdisystem og brugte et sexagesimalt talsystem, som stadig er i brug i dag til at måle vinkler og tid.

Archimedes brugte udmattelsesmetoden , afbildet her, for at tilnærme værdien af ​​pi .

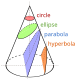
Begyndende i det 6. århundrede f.Kr. med pythagoræerne , med græsk matematik begyndte de gamle grækere en systematisk undersøgelse af matematik som et emne i sig selv. Omkring 300 f.Kr. introducerede Euklid den aksiomatiske metode, der stadig bruges i matematik i dag, bestående af definition, aksiom, sætning og bevis. Hans bog, Elementer , anses for at være den mest succesrige og indflydelsesrige lærebog nogensinde. Antikkens største matematiker anses ofte for at være Arkimedes (ca. 287-212 f.Kr.) fra Syracusa . Han udviklede formler til beregning af overfladearealet og volumen af ​​rotationsfaste stoffer og brugte udmattelsesmetoden til at beregne arealet under buen af ​​en parabel med summering af en uendelig række , på en måde, der ikke er alt for ulig fra moderne calculus. Andre bemærkelsesværdige præstationer af græsk matematik er keglesnit ( Apollonius af Perga , 3. århundrede f.Kr.), trigonometri ( Hipparchus af Nicaea , 2. århundrede f.Kr.) og begyndelsen af ​​algebra ( Diophantus , 3. århundrede e.Kr.).

Tallene brugt i Bakhshali-manuskriptet , dateret mellem det 2. århundrede f.Kr. og det 2. århundrede e.Kr.

Det hindu-arabiske talsystem og reglerne for brugen af ​​dets operationer, der er i brug over hele verden i dag, udviklede sig i løbet af det første årtusinde e.Kr. i Indien og blev overført til den vestlige verden via islamisk matematik . Andre bemærkelsesværdige udviklinger inden for indisk matematik omfatter den moderne definition og tilnærmelse af sinus og cosinus og en tidlig form for uendelig række .

En side fra al-Khwārizmīs algebra

Leonardo Fibonacci , den italienske matematiker, der introducerede det hindu-arabiske talsystem opfundet mellem det 1. og 4. århundrede af indiske matematikere, til den vestlige verden.

Under islams guldalder , især i det 9. og 10. århundrede, oplevede matematik mange vigtige innovationer, der byggede på græsk matematik. Den mest bemærkelsesværdige præstation af islamisk matematik var udviklingen af ​​algebra . Andre resultater fra den islamiske periode omfatter fremskridt inden for sfærisk trigonometri og tilføjelsen af ​​decimalkommaet til det arabiske talsystem. Mange bemærkelsesværdige matematikere fra denne periode var persiske, såsom Al-Khwarismi , Omar Khayyam og Sharaf al-Dīn al-Ṭūsī .

I den tidlige moderne periode begyndte matematikken at udvikle sig i et accelererende tempo i Vesteuropa . Udviklingen af ​​calculus af Isaac Newton og Gottfried Leibniz i det 17. århundrede revolutionerede matematikken. Leonhard Euler var den mest bemærkelsesværdige matematiker i det 18. århundrede og bidrog med adskillige teoremer og opdagelser. Den måske fremmeste matematiker i det 19. århundrede var den tyske matematiker Carl Gauss , som ydede adskillige bidrag til områder som algebra , analyse , differentialgeometri , matrixteori , talteori og statistik . I det tidlige 20. århundrede transformerede Kurt Gödel matematik ved at udgive sine ufuldstændighedssætninger , som til dels viser, at ethvert konsistent aksiomatisk system – hvis det er kraftigt nok til at beskrive aritmetik – vil indeholde sande påstande, som ikke kan bevises.

Matematik er siden blevet meget udvidet, og der har været et frugtbart samspil mellem matematik og naturvidenskab , til gavn for begge. Matematiske opdagelser bliver stadig gjort den dag i dag. Ifølge Mikhail B. Sevryuk i januar 2006-udgaven af ​​Bulletin of the American Mathematical Society : "Antallet af artikler og bøger, der er inkluderet i Mathematical Reviews -databasen siden 1940 (det første driftsår for MR) er nu mere end 1,9 millioner, og mere end 75 tusinde genstande tilføjes til databasen hvert år. Det overvældende flertal af værker i dette hav indeholder nye matematiske teoremer og deres beviser ."

Etymologi

Ordet matematik kommer fra oldgræsk máthēma ( μάθημα ), der betyder "det, der er lært", "det man får at vide", deraf også "studium" og "videnskab". Ordet for "matematik" kom til at have den snævrere og mere tekniske betydning "matematisk studie" selv i klassisk tid. Dens adjektiv er mathēmatikós ( μαθηματικός ), der betyder "relateret til læring" eller "studerende", som ligeledes yderligere kom til at betyde "matematisk". Især mathēmatikḗ tékhnē ( μαθηματικὴ τέχνη ; latin : ars mathematica ) betød "den matematiske kunst."

På samme måde var en af ​​de to vigtigste tankegange i pythagoreanismen kendt som mathēmatikoi (μαθηματικοί) – som på det tidspunkt betød "lærende" snarere end "matematikere" i moderne forstand.

På latin og på engelsk indtil omkring 1700 betød udtrykket matematik mere almindeligt " astrologi " (eller nogle gange " astronomi ") snarere end "matematik"; betydningen ændrede sig gradvist til dens nuværende fra omkring 1500 til 1800. Dette har resulteret i flere fejloversættelser. For eksempel bliver Sankt Augustins advarsel om, at kristne skal passe på mathematici , hvilket betyder astrologer, nogle gange fejloversat som en fordømmelse af matematikere.

Den tilsyneladende flertalsform på engelsk går ligesom den franske flertalsform les mathématiques (og den mindre almindeligt anvendte entalsafledning la mathématique ), tilbage til det latinske intetkøn flertal mathematica ( Cicero ), baseret på den græske flertalsform ta mathēmatiká ( τὰ μαθτιη ), καν μαθιηκ. brugt af Aristoteles (384-322 f.Kr.), og betyder groft sagt "alt matematisk", selvom det er sandsynligt, at engelsk kun lånte adjektivet matematic(al) og dannede navneordet matematik på ny efter mønsteret af fysik og metafysik , som var arvet fra græsk. På engelsk tager navneordet matematik et verbum i ental. Det er ofte forkortet til matematik eller, i Nordamerika, matematik .

Matematikkens filosofi

Der er ingen generel konsensus om matematikkens nøjagtige definition eller epistemologiske status . Aristoteles definerede matematik som "videnskaben om kvantitet", og denne definition herskede indtil det 18. århundrede. Aristoteles bemærkede dog også, at et fokus på kvantitet alene ikke kan skelne matematik fra videnskaber som fysik; efter hans opfattelse adskiller abstraktion og undersøgelse af kvantitet som en egenskab "adskillelig i tanken" fra virkelige tilfælde matematikken.

I det 19. århundrede, da matematikstudiet øgedes i strenghed og begyndte at behandle abstrakte emner som gruppeteori og projektiv geometri , som ikke har nogen entydig relation til mængde og måling, begyndte matematikere og filosoffer at foreslå en række nye definitioner .

Rigtig mange professionelle matematikere interesserer sig ikke for en definition af matematik eller anser den for udefinerbar. Der er ikke engang konsensus om, hvorvidt matematik er en kunst eller en videnskab. Nogle siger bare: "Matematik er det, matematikere gør."

Tre førende typer

Tre førende typer af definitioner af matematik i dag kaldes logiker , intuitionist og formalist , som hver afspejler en anden filosofisk tankegang. Alle har alvorlige fejl, ingen har udbredt accept, og ingen forsoning ser ud til at være mulig.

Logistiske definitioner

En tidlig definition af matematik i form af logik var Benjamin Peirces (1870): "videnskaben, der drager nødvendige konklusioner." I Principia Mathematica fremførte Bertrand Russell og Alfred North Whitehead det filosofiske program kendt som logicisme og forsøgte at bevise, at alle matematiske begreber, udsagn og principper kan defineres og bevises udelukkende i form af symbolsk logik . Et eksempel på en logistisk definition af matematik er Russells (1903) "All Mathematics is Symbolic Logic."

Intuitionistiske definitioner

Intuitionistiske definitioner, der udvikler sig fra matematikeren LEJ Brouwers filosofi , identificerer matematik med visse mentale fænomener. Et eksempel på en intuitionistisk definition er "Matematik er den mentale aktivitet, der består i at udføre konstruktioner efter hinanden." En ejendommelighed ved intuitionisme er, at den afviser nogle matematiske ideer, der anses for gyldige ifølge andre definitioner. Især mens andre matematiske filosofier tillader objekter, der kan bevises at eksistere, selvom de ikke kan konstrueres, tillader intuitionisme kun matematiske objekter, som man faktisk kan konstruere. Intuitionister afviser også loven om udelukket mellem (dvs. ). Selvom denne holdning tvinger dem til at afvise en almindelig version af bevis ved modsigelse som en levedygtig bevismetode, nemlig slutningen af ​​fra , er de stadig i stand til at udlede fra . For dem er et strengt svagere udsagn end . ${\displaystyle P\vee \neg P}$${\displaystyle P}$${\displaystyle \neg P\to \bot }$${\displaystyle \neg P}$${\displaystyle P\to \bot }$${\displaystyle \neg (\neg P)}$${\displaystyle P}$

Formalistiske definitioner

Formalistiske definitioner identificerer matematik med dens symboler og reglerne for at arbejde på dem. Haskell Curry definerede matematik simpelthen som "videnskaben om formelle systemer". Et formelt system er et sæt af symboler, eller tokens , og nogle regler for, hvordan tokens skal kombineres til formler . I formelle systemer har ordet aksiom en særlig betydning, der er forskellig fra den almindelige betydning af "en indlysende sandhed", og bruges til at henvise til en kombination af tokens, der er inkluderet i et givet formelt system uden at skulle afledes ved hjælp af systemets regler.

Matematik som videnskab

Carl Friedrich Gauss , kendt som matematikernes fyrste

Den tyske matematiker Carl Friedrich Gauss omtalte matematik som "videnskabernes dronning". For nylig har Marcus du Sautoy kaldt matematik for "videnskabens dronning ... den vigtigste drivkraft bag videnskabelig opdagelse". Filosoffen Karl Popper bemærkede, at "de fleste matematiske teorier, ligesom de inden for fysik og biologi , er hypotetisk - deduktive : ren matematik viser sig derfor at være meget tættere på naturvidenskaberne, hvis hypoteser er formodninger, end det så ud til selv for nylig." Popper bemærkede også, at "jeg vil bestemt kun indrømme et system som empirisk eller videnskabeligt, hvis det er i stand til at blive testet af erfaring."

Matematik har meget til fælles med mange områder inden for de fysiske videnskaber, især udforskningen af ​​de logiske konsekvenser af antagelser. Intuition og eksperimenter spiller også en rolle i formuleringen af ​​formodninger i både matematik og (andre) videnskaber. Eksperimentel matematik bliver ved med at vokse i betydning inden for matematik, og beregning og simulering spiller en stigende rolle i både naturvidenskab og matematik.

Flere forfattere mener, at matematik ikke er en videnskab, fordi den ikke er afhængig af empiriske beviser . Matematikernes meninger om dette spørgsmål er forskellige. Mange matematikere føler, at at kalde deres område for en videnskab er at bagatellisere betydningen af ​​dets æstetiske side og dets historie i de traditionelle syv liberale kunster ; andre føler, at at ignorere dens forbindelse til videnskaberne er at vende det blinde øje til, at grænsefladen mellem matematik og dens anvendelser inden for naturvidenskab og ingeniørvidenskab har drevet meget udvikling inden for matematikken. En måde, hvorpå denne forskel i synspunkter udspiller sig, er i den filosofiske debat om, hvorvidt matematik er skabt (som i kunst) eller opdaget (som i videnskab). I praksis er matematikere typisk grupperet med videnskabsmænd på bruttoniveau, men adskilt på finere niveauer. Dette er et af mange spørgsmål, der overvejes i matematikfilosofien .

Inspiration, ren og anvendt matematik og æstetik

Isaac Newton (til venstre) og Gottfried Wilhelm Leibniz udviklede infinitesimalregning.

Matematik udspringer af mange forskellige slags problemer. Først blev disse fundet i handel, landmåling , arkitektur og senere astronomi ; i dag stiller alle videnskaber problemer studeret af matematikere, og mange problemer opstår inden for matematikken selv. For eksempel opfandt fysikeren Richard Feynman den sti-integrale formulering af kvantemekanikken ved hjælp af en kombination af matematisk ræsonnement og fysisk indsigt, og nutidens strengteori , en videnskabelig teori i stadig udvikling, som forsøger at forene de fire grundlæggende naturkræfter , fortsætter med at inspirere. ny matematik.

Noget matematik er kun relevant i det område, der inspirerede det, og bruges til at løse yderligere problemer på dette område. Men ofte viser matematik inspireret af ét område sig nyttig på mange områder og slutter sig til den generelle bestand af matematiske begreber. Der skelnes ofte mellem ren matematik og anvendt matematik . Men rene matematikemner viser sig ofte at have anvendelser, f.eks . talteori i kryptografi .

Denne bemærkelsesværdige kendsgerning, at selv den "reneste" matematik ofte viser sig at have praktiske anvendelser, er, hvad fysikeren Eugene Wigner har kaldt " matematikkens urimelige effektivitet ". Matematikkens filosof Mark Steiner har skrevet meget om denne sag og anerkender, at matematikkens anvendelighed udgør "en udfordring for naturalismen." For matematikfilosoffen Mary Leng er den kendsgerning, at den fysiske verden handler i overensstemmelse med diktaterne af ikke-kausale matematiske enheder, der eksisterer hinsides universet, "et lykkeligt tilfælde". På den anden side, for nogle anti-realister , afspejler forbindelser, som er erhvervet blandt matematiske ting, blot de forbindelser, der erhverves mellem objekter i universet, så der er ingen "lykkelig tilfældighed".

Som i de fleste studieområder har eksplosionen af ​​viden i den videnskabelige tidsalder ført til specialisering: Der er nu hundredvis af specialiserede områder inden for matematik, og den seneste matematiske fagklassifikation strækker sig over 46 sider. Adskillige områder af anvendt matematik er smeltet sammen med relaterede traditioner uden for matematikken og er blevet discipliner i sig selv, herunder statistik, operationsforskning og datalogi .

For dem, der er matematisk tilbøjelige, er der ofte et klart æstetisk aspekt ved meget af matematikken. Mange matematikere taler om matematikkens elegance , dens iboende æstetik og indre skønhed. Enkelhed og almenhed værdsættes. Der er skønhed i et enkelt og elegant bevis , såsom Euklids bevis på, at der er uendeligt mange primtal , og i en elegant numerisk metode , der fremskynder beregningen, såsom den hurtige Fourier-transformation . GH Hardy i A Mathematician's Apology udtrykte troen på, at disse æstetiske overvejelser i sig selv er tilstrækkelige til at retfærdiggøre studiet af ren matematik. Han identificerede kriterier som betydning, uventethed, uundgåelighed og økonomi som faktorer, der bidrager til en matematisk æstetik. Matematisk forskning søger ofte kritiske træk ved et matematisk objekt. En sætning udtrykt som en karakterisering af et objekt ved disse træk er prisen. Eksempler på særligt kortfattede og åbenbarende matematiske argumenter er blevet publiceret i Proofs from THE BOOK .

Populariteten af ​​rekreativ matematik er endnu et tegn på den fornøjelse, mange finder ved at løse matematiske spørgsmål. Ved den anden sociale yderlighed fortsætter filosoffer med at finde problemer i matematikfilosofien , såsom arten af ​​matematiske beviser .

Notation, sprog og stringens

Leonhard Euler skabte og populariserede meget af den matematiske notation, der bruges i dag.

Det meste af den matematiske notation, der bruges i dag, blev opfundet efter det 15. århundrede. Før det blev matematik skrevet ud i ord, hvilket begrænsede matematisk opdagelse. Euler (1707-1783) var ansvarlig for mange af disse notationer. Moderne notation gør matematik effektiv for den professionelle, mens begyndere ofte finder det skræmmende.

Matematisk sprog giver en mere præcis betydning for almindelige ord som eller og kun, end de har i daglig tale. Andre udtryk som åbent og felt er på én gang præcise og henviser også til specifikke begreber, der kun findes i matematik. Matematisk sprog omfatter også mange tekniske termer såsom homeomorphism og integrable , der ikke har nogen betydning uden for matematik. Derudover hører stenografiske sætninger som iff for " hvis og kun hvis " til matematisk jargon . Denne specielle notation og tekniske ordforråd er både præcis og kortfattet, hvilket gør det muligt at arbejde med ideer af uforholdsmæssig kompleksitet. Matematikere omtaler denne præcision af sprog og logik som "rigor".

Gyldigheden af ​​matematiske beviser er grundlæggende et spørgsmål om strenghed . Matematikere ønsker, at deres sætninger følger af aksiomer ved hjælp af systematisk ræsonnement. Dette for at undgå fejlagtige "sætninger", baseret på fejlbarlige intuitioner, som er opstået mange gange i matematikkens historie. Den stringens, der forventes i matematik, har varieret over tid: Grækerne forventede detaljerede argumenter, men i Isaac Newtons storhedstid var de anvendte metoder mindre strenge. Problemer iboende i definitionerne brugt af Newton førte til en genopblussen af ​​omhyggelig analyse og formelle beviser i det 19. århundrede. Misforståelse af strenghed er en bemærkelsesværdig årsag til nogle af de almindelige misforståelser om matematik.

På trods af matematikkens koncision kræver mange beviser hundredvis af sider at udtrykke. Fremkomsten af ​​computerstøttede beviser har gjort det muligt for bevislængder at udvide sig yderligere. Assisterede beviser kan være fejlagtige, hvis bevissoftwaren har fejl, og hvis de er lange, svære at kontrollere. På den anden side giver korrekturassistenter mulighed for at verificere detaljer, der ikke kan gives i et håndskrevet bevis, og giver sikkerhed for rigtigheden af ​​lange beviser som f.eks. Feit-Thompson-sætningen på 255 sider .

Traditionelt blev aksiomer tænkt som "selvindlysende sandheder". Men på et formelt niveau er et aksiom blot en række af symboler, som kun har en iboende betydning i sammenhæng med de afledbare formler i et aksiomatisk system . Hilberts program forsøgte at sætte matematik på et fast aksiomatisk grundlag, men Gödels ufuldstændighedssætning ophævede det og viste, at ethvert (tilstrækkeligt kraftfuldt) aksiomatisk system har uafgørlige formler; og derfor er aksiomatisering af matematik umulig. Ikke desto mindre forestilles matematik ofte (så vidt det formelle indhold) ikke er andet end mængdeteori i en eller anden aksiomatisering, i den forstand at enhver matematisk udsagn eller bevis kunne støbes ind i formler inden for mængdeteori.

Priser

Forsiden af ​​Fields Medaljen

Nok den mest prestigefyldte pris inden for matematik er Fields Medal , etableret i 1936 og uddelt hvert fjerde år (undtagen omkring Anden Verdenskrig) til så mange som fire personer. Fields-medaljen betragtes ofte som en matematisk ækvivalent til Nobelprisen.

Ulveprisen i matematik , der blev indstiftet i 1978, anerkender livspræstationer. En anden stor international pris, Abelprisen , blev indstiftet i 2002 og uddelt første gang i 2003. Chern-medaljen blev indført i 2010 for at anerkende livsglæde. Disse priser tildeles som en anerkendelse af et bestemt arbejde, som kan være innovativt eller give en løsning på et udestående problem inden for et etableret felt.

En berømt liste over 23 åbne problemer , kaldet " Hilberts problemer ", blev udarbejdet i 1900 af den tyske matematiker David Hilbert . Denne liste opnåede stor berømthed blandt matematikere, og mindst tretten af ​​problemerne er nu løst. En ny liste med syv vigtige problemer, med titlen " Millennium Prize Problems ", blev offentliggjort i 2000. Kun et af dem, Riemann-hypotesen , kopierer et af Hilberts problemer. En løsning på ethvert af disse problemer medfører en belønning på 1 million dollar. I øjeblikket er kun et af disse problemer, Poincaré-formodningen , blevet løst.

Se også

Noter

Referencer

Bibliografi

Yderligere læsning