Routhian mekanik - Routhian mechanics

Edward John Routh , 1831–1907.

En del af en serie om
Klassisk mekanik
${\ displaystyle {\ textbf {F}} = {\ frac {d} {dt}} (m {\ textbf {v}})}$ Anden lov om bevægelse
Historie Tidslinje Lærebøger
Grene
Grundlæggende
Formuleringer
Kerneemner
Rotation
Forskere
Kategorier
v t e

I klassisk mekanik er Rouths procedure eller Routhian mekanik en hybrid formulering af Lagrangian mekanik og Hamiltonian mekanik udviklet af Edward John Routh. Tilsvarende er Routhian den funktion, der erstatter både Lagrangian- og Hamiltonian- funktionerne. Som med resten af ​​den analytiske mekanik svarer den routhiske mekanik fuldstændigt til den newtonske mekanik, alle andre formuleringer af klassisk mekanik og introducerer ingen ny fysik. Det giver en alternativ måde at løse mekaniske problemer på.

Definitioner

Routhianen, som Hamiltonian, kan fås fra en Legendre-transformation af Lagrangian og har en lignende matematisk form som Hamiltonianen, men er ikke nøjagtig den samme. Forskellen mellem de Lagrangian, Hamiltonian og Routhian funktioner er deres variabler. For et givet sæt generaliserede koordinater, der repræsenterer frihedsgraderne i systemet, er Lagrangian en funktion af koordinaterne og hastighederne, mens Hamiltonian er en funktion af koordinaterne og momentaerne.

Routhian adskiller sig fra disse funktioner, idet nogle koordinater vælges til at have tilsvarende generaliserede hastigheder, resten for at have tilsvarende generaliserede momenta. Dette valg er vilkårligt og kan gøres for at forenkle problemet. Det har også den konsekvens, at de routhiske ligninger er nøjagtigt de Hamiltoniske ligninger for nogle koordinater og tilsvarende momenta, og de Lagrangiske ligninger for resten af ​​koordinaterne og deres hastigheder. I begge tilfælde erstattes Lagrangian og Hamiltonian-funktionerne med en enkelt funktion, den routhiske. Hele sættet har således fordelene ved begge sæt ligninger med bekvemmeligheden ved at opdele et sæt koordinater til Hamilton-ligningerne og resten til Lagrangian-ligningerne.

I tilfælde af Lagrangian-mekanik, de generelle koordinater q ₁ , q ₂ , ... og de tilsvarende hastigheder dq ₁ / dt , dq ₂ / dt , ... og muligvis tid t , indtast Lagrangian,

${\ displaystyle L (q_ {1}, q_ {2}, \ ldots, {\ dot {q}} _ {1}, {\ dot {q}} _ {2}, \ ldots, t) \ ,, \ quad {\ dot {q}} _ {i} = {\ frac {dq_ {i}} {dt}} \ ,,}$

hvor overdots betegne tidsafledte .

I hamiltons mekanik går de generaliserede koordinater q ₁ , q ₂ , ... og den tilsvarende generaliserede momenta p ₁ , p ₂ , ... og muligvis tid ind i Hamilton,

${\ displaystyle H (q_ {1}, q_ {2}, \ ldots, p_ {1}, p_ {2}, \ ldots, t) = \ sum _ {i} {\ dot {q}} _ {i } p_ {i} -L (q_ {1}, q_ {2}, \ ldots, {\ dot {q}} _ {1} (p_ {1}), {\ dot {q}} _ {2} (p_ {2}), \ ldots, t) \ ,, \ quad p_ {i} = {\ frac {\ partial L} {\ partial {\ dot {q}} _ {i}}} \ ,,}$

hvor den anden ligning er definitionen af den generelle momentum p _jeg svarende til koordinatsystemet q _i ( partielt afledte er betegnet ved anvendelse ∂ ). Hastighederne dq _i / dt udtrykkes som funktioner i deres tilsvarende momenta ved at invertere deres definerende relation. I denne sammenhæng siges det at p _i er momentumet "kanonisk konjugeret" til q _i .

Routhianen er mellemliggende mellem L og H ; nogle koordinater q ₁ , q ₂ , ..., q _n vælges til at have tilsvarende generaliserede momenta p ₁ , p ₂ , ..., p _n , resten af ​​koordinaterne ζ ₁ , ζ ₂ , ..., ζ _s at have generaliserede hastigheder dζ ₁ / dt , dζ ₂ / dt , ..., dζ _s / dt , og tiden kan vises eksplicit;

hvor igen den generelle hastighed dq _i / dt skal udtrykkes som en funktion af generaliseret momentum p _i via sin afgrænser forhold. Valget af hvilke n koordinater der skal have tilsvarende momenta ud af n + s koordinaterne er vilkårlig.

Ovenstående bruges af Landau og Lifshitz og Goldstein . Nogle forfattere kan definere den routhianske som den negative af ovenstående definition.

I betragtning af længden af ​​den generelle definition er en mere kompakt notation at bruge fed skrift til tupler (eller vektorer) af variablerne, således at q = ( q ₁ , q ₂ , ..., q _n ) , ζ = ( ζ ₁ , ζ ₂ , ..., ζ _s ) , p = ( p ₁ , p ₂ , ..., p _n ) og d ζ / dt = ( dζ ₁ / dt , dζ ₂ / dt , ..., dζ _s / dt ) , således at

${\ displaystyle R (\ mathbf {q}, {\ boldsymbol {\ zeta}}, \ mathbf {p}, {\ dot {\ boldsymbol {\ zeta}}}, t) = \ mathbf {p} \ cdot { \ dot {\ mathbf {q}}} - L (\ mathbf {q}, {\ boldsymbol {\ zeta}}, {\ dot {\ mathbf {q}}}, {\ dot {\ boldsymbol {\ zeta} }}, t) \ ,,}$

hvor · er prikproduktet defineret på tuplerne, for det specifikke eksempel, der vises her:

${\ displaystyle \ mathbf {p} \ cdot {\ dot {\ mathbf {q}}} = \ sum _ {i = 1} ^ {n} p_ {i} {\ dot {q}} _ {i} \ ,.}$

Bevægelsesligninger

Til reference er Euler-Lagrange-ligningerne for s frihedsgrader et sæt s koblet anden ordens almindelige differentialligninger i koordinaterne

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {q}} _ {j}}} = {\ frac {\ partial L} {\ partial q_ {j}}} \ ,,}$

hvor j = 1, 2, ..., s og de Hamiltoniske ligninger for n frihedsgrader er et sæt af 2 n koblede ordens normale ordens differentialligninger i koordinaterne og momenta

${\ displaystyle {\ dot {q}} _ {i} = {\ frac {\ partial H} {\ partial p_ {i}}} \ ,, \ quad {\ dot {p}} _ {i} = - {\ frac {\ partial H} {\ partial q_ {i}}} \ ,.}$

Nedenfor opnås de routhiske bevægelsesligninger på to måder, i processen findes andre nyttige derivater, der kan bruges andre steder.

To frihedsgrader

Overvej tilfældet med et system med to frihedsgrader , q og ζ , med generaliserede hastigheder dq / dt og dζ / dt , og Lagrangian er tidsafhængig. (Generaliseringen til et hvilket som helst antal frihedsgrader følger nøjagtigt den samme procedure som med to). Systemets Lagrangian har formen

${\ displaystyle L (q, \ zeta, {\ dot {q}}, {\ dot {\ zeta}}, t)}$

Den forskellen af L er

${\ displaystyle dL = {\ frac {\ partial L} {\ partial q}} dq + {\ frac {\ partial L} {\ partial \ zeta}} d \ zeta + {\ frac {\ partial L} {\ partial {\ dot {q}}}} d {\ dot {q}} + {\ frac {\ partial L} {\ partial {\ dot {\ zeta}}}} d {\ dot {\ zeta}} + { \ frac {\ partial L} {\ partial t}} dt \ ,.}$

Skift nu variabler fra sættet ( q , ζ , dq / dt , dζ / dt ) til ( q , ζ , p , dζ / dt ) ved blot at skifte hastigheden dq / dt til momentum p . Denne ændring af variabler i differentierne er Legendre-transformation . Differentialet for den nye funktion til erstatning af L vil være en sum af forskelle i dq , dζ , dp , d ( dζ / dt ) og dt . Brug af definitionen af ​​generaliseret momentum og Lagrange's ligning for koordinaten q :

${\ displaystyle p = {\ frac {\ partial L} {\ partial {\ dot {q}}}} \ ,, \ quad {\ dot {p}} = {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {q}}}} = {\ frac {\ partial L} {\ partial q}}}$

vi har

${\ displaystyle dL = {\ dot {p}} dq + {\ frac {\ partial L} {\ partial \ zeta}} d \ zeta + pd {\ dot {q}} + {\ frac {\ partial L} { \ partial {\ dot {\ zeta}}}} d {\ dot {\ zeta}} + {\ frac {\ partial L} {\ partial t}} dt}$

og at erstatte pd ( dq / dt ) med ( dq / dt ) dp , huske produktreglen for differentier og erstatte

${\ displaystyle pd {\ dot {q}} = d ({\ dot {q}} p) - {\ dot {q}} dp}$

for at opnå differentieringen af ​​en ny funktion med hensyn til det nye sæt af variabler:

${\ displaystyle d (Lp {\ dot {q}}) = {\ dot {p}} dq + {\ frac {\ partial L} {\ partial \ zeta}} d \ zeta - {\ dot {q}} dp + {\ frac {\ partial L} {\ partial {\ dot {\ zeta}}}} d {\ dot {\ zeta}} + {\ frac {\ partial L} {\ partial t}} dt \ ,.}$

Introduktion til Routhian

${\ displaystyle R (q, \ zeta, p, {\ dot {\ zeta}}, t) = p {\ dot {q}} (p) -L}$

hvor hastigheden dq / dt igen er en funktion af momentum p , har vi

${\ displaystyle dR = - {\ dot {p}} dq - {\ frac {\ partial L} {\ partial \ zeta}} d \ zeta + {\ dot {q}} dp - {\ frac {\ partial L } {\ partial {\ dot {\ zeta}}}} d {\ dot {\ zeta}} - {\ frac {\ partial L} {\ partial t}} dt \ ,,}$

men fra ovenstående definition er differentieringen af ​​den routhianske

${\ displaystyle dR = {\ frac {\ partial R} {\ partial q}} dq + {\ frac {\ partial R} {\ partial \ zeta}} d \ zeta + {\ frac {\ partial R} {\ partial p}} dp + {\ frac {\ partial R} {\ partial {\ dot {\ zeta}}}} d {\ dot {\ zeta}} + {\ frac {\ partial R} {\ partial t}} dt \ ,.}$

Sammenligning af koefficienterne for differentierne dq , dζ , dp , d ( dζ / dt ) og dt , er resultaterne Hamiltons ligninger for koordinaten q ,

${\ displaystyle {\ dot {q}} = {\ frac {\ partial R} {\ partial p}} \ ,, \ quad {\ dot {p}} = - {\ frac {\ partial R} {\ partial q}} \ ,,}$

og Lagranges ligning for koordinaten ζ

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial R} {\ partial {\ dot {\ zeta}}}} = {\ frac {\ partial R} {\ partial \ zeta}} }$

som følger af

${\ displaystyle {\ frac {\ partial L} {\ partial \ zeta}} = - {\ frac {\ partial R} {\ partial \ zeta}} \ ,, \ quad {\ frac {\ partial L} {\ delvis {\ dot {\ zeta}}}} = - {\ frac {\ partial R} {\ partial {\ dot {\ zeta}}}} \ ,,}$

og tage det samlede tidsafledte af den anden ligning og lig med den første. Bemærk, at den routhianske erstatter de hamiltonske og lagrangiske funktioner i alle bevægelsesligningerne.

Den resterende ligning angiver, at deltidsderivaterne af L og R er negative

${\ displaystyle {\ frac {\ partial L} {\ partial t}} = - {\ frac {\ partial R} {\ partial t}} \ ,.}$

Et hvilket som helst antal frihedsgrader

For n + s koordinater som defineret ovenfor med Routhian

${\ displaystyle R (q_ {1}, \ ldots, q_ {n}, \ zeta _ {1}, \ ldots, \ zeta _ {s}, p_ {1}, \ ldots, p_ {n}, {\ prik {\ zeta}} _ {1}, \ ldots, {\ dot {\ zeta}} _ {s}, t) = \ sum _ {i = 1} ^ {n} p_ {i} {\ dot { q}} _ {i} (p_ {i}) - L}$

bevægelsesligningerne kan afledes ved en legendre-transformation af denne routhian som i det foregående afsnit, men en anden måde er blot at tage de delvise derivater af R med hensyn til koordinaterne q _i og ζ _j , momenta p _i og hastigheder dζ _j / dt , hvor i = 1, 2, ..., n og j = 1, 2, ..., s . Derivaterne er

${\ displaystyle {\ frac {\ partial R} {\ partial q_ {i}}} = - {\ frac {\ partial L} {\ partial q_ {i}}} = - {\ frac {d} {dt} } {\ frac {\ partial L} {\ partial {\ dot {q}} _ {i}}} = - {\ dot {p}} _ {i}}$

${\ displaystyle {\ frac {\ partial R} {\ partial p_ {i}}} = {\ dot {q}} _ {i}}$

${\ displaystyle {\ frac {\ partial R} {\ partial \ zeta _ {j}}} = - {\ frac {\ partial L} {\ partial \ zeta _ {j}}} \ ,,}$

${\ displaystyle {\ frac {\ partial R} {\ partial {\ dot {\ zeta}} _ {j}}} = - {\ frac {\ partial L} {\ partial {\ dot {\ zeta}} _ {j}}} \ ,,}$

${\ displaystyle {\ frac {\ partial R} {\ partial t}} = - {\ frac {\ partial L} {\ partial t}} \ ,.}$

De to første er identisk Hamilton-ligningerne. Ligning af det samlede tidsafledte af det fjerde sæt ligninger med det tredje (for hver værdi af j ) giver de Lagrangiske ligninger. Den femte er bare den samme sammenhæng mellem tidspartielle derivater som før. At opsummere

Det samlede antal ligninger er 2 n + s , der er 2 n Hamiltonian ligninger plus s Lagrange ligninger.

Energi

Da Lagrangian har de samme enheder som energi , er enhederne i Routhian også energi. I SI-enheder er dette Joule .

At tage det samlede tidsafledte af Lagrangian fører til det generelle resultat

${\ displaystyle {\ frac {\ partial L} {\ partial t}} = {\ frac {d} {dt}} \ left (\ sum _ {i = 1} ^ {n} {\ dot {q}} _ {i} {\ frac {\ partial L} {\ partial {\ dot {q}} _ {i}}} + \ sum _ {j = 1} ^ {s} {\ dot {\ zeta}} _ {j} {\ frac {\ partial L} {\ partial {\ dot {\ zeta}} _ {j}}} - L \ right) \ ,.}$

Hvis Lagrangian er uafhængig af tid, er den delvise tidsderivat af Lagrangian nul, ∂ L / ∂ t = 0 , så mængden under den samlede tidsderivat i parentes skal være en konstant, det er systemets samlede energi

${\ displaystyle E = \ sum _ {i = 1} ^ {n} {\ dot {q}} _ {i} {\ frac {\ partial L} {\ partial {\ dot {q}} _ {i} }} + \ sum _ {j = 1} ^ {s} {\ dot {\ zeta}} _ {j} {\ frac {\ partial L} {\ partial {\ dot {\ zeta}} _ {j} }} - L \ ,.}$

(Hvis der er eksterne felter, der interagerer med systemets bestanddele, kan de variere i hele rummet, men ikke i tid). Dette udtryk kræver delderivater af L med hensyn til alle hastigheder dq _i / dt og dζ _j / dt . Under den samme betingelse, at R er tidsuafhængig, er energien i form af den routhianske lidt enklere, og erstatter definitionen af R og de delvise derivater af R med hensyn til hastighederne dζ _j / dt ,

${\ displaystyle E = R- \ sum _ {j = 1} ^ {s} {\ dot {\ zeta}} _ {j} {\ frac {\ partial R} {\ partial {\ dot {\ zeta}} _ {j}}} \ ,.}$

Bemærk kun de delvise derivater af R med hensyn til hastighederne dζ _j / dt er nødvendige. I tilfælde af at s = 0 og den routhianske er eksplicit tidsuafhængig, så er E = R , det vil sige den routhianske er lig med systemets energi. Samme udtryk for R i, når s = 0 er også Hamiltonske, så i alt E = R = H .

Hvis routhianeren har eksplicit tidsafhængighed, er systemets samlede energi ikke konstant. Det generelle resultat er

${\ displaystyle {\ frac {\ partial R} {\ partial t}} = {\ dfrac {d} {dt}} \ left (R- \ sum _ {j = 1} ^ {s} {\ dot {\ zeta}} _ {j} {\ frac {\ partial R} {\ partial {\ dot {\ zeta}} _ {j}}} \ right) \ ,,}$

som kan afledes fra den samlede tid derivat af R på samme måde som for L .

Cykliske koordinater

Ofte tilbyder den routhiske tilgang ikke nogen fordel, men et bemærkelsesværdigt tilfælde, hvor dette er nyttigt, er når et system har cykliske koordinater (også kaldet "uvidende koordinater"), pr. Definition de koordinater, der ikke vises i den oprindelige Lagrangian. Lagrangians ligninger er stærke resultater, der ofte bruges i teori og praksis, da bevægelsesligningerne i koordinaterne er lette at oprette. Men hvis der forekommer cykliske koordinater, vil der stadig være ligninger, der skal løses for alle koordinaterne, inklusive de cykliske koordinater på trods af deres fravær i Lagrangian. Hamilton-ligningerne er nyttige teoretiske resultater, men mindre nyttige i praksis, fordi koordinater og momenta hænger sammen i løsningerne - efter løsning af ligningerne skal koordinaterne og momentan fjernes fra hinanden. Ikke desto mindre er de Hamilton-ligninger perfekt egnede til cykliske koordinater, fordi ligningerne i de cykliske koordinater forsvinder trivielt og kun efterlader ligningerne i de ikke-cykliske koordinater.

Den routhiske tilgang har det bedste fra begge tilgange, fordi cykliske koordinater kan opdeles til Hamilton-ligningerne og elimineres, hvilket efterlader de ikke-cykliske koordinater, der skal løses fra de Lagrangiske ligninger. Samlet set skal færre ligninger løses i forhold til Lagrangian-tilgangen.

Den Routhian formulering er nyttig til systemer med cykliske koordinater , fordi per definition disse koordinater ikke træder L og dermed R . De tilsvarende partielle derivater af L og R med hensyn til disse koordinater er nul, hvilket svarer til det tilsvarende generaliserede momenta reduceret til konstanter. For at gøre dette konkret, hvis q _i alle er cykliske koordinater, og ζ _j alle er ikke-cykliske, så

${\ displaystyle {\ frac {\ partial L} {\ partial q_ {i}}} = {\ dot {p}} _ {i} = - {\ frac {\ partial R} {\ partial q_ {i}} } = 0 \ quad \ Rightarrow \ quad p_ {i} = \ alpha _ {i} \ ,,}$

hvor a _jeg er konstanter. Med disse konstanter substitueret til routhianen, er R en funktion af kun de ikke-cykliske koordinater og hastigheder (og generelt også tiden)

${\ displaystyle R (\ zeta _ {1}, \ ldots, \ zeta _ {s}, \ alpha _ {1}, \ ldots, \ alpha _ {n}, {\ dot {\ zeta}} _ {1 }, \ ldots, {\ dot {\ zeta}} _ {s}, t) = \ sum _ {i = 1} ^ {n} \ alpha _ {i} {\ dot {q}} _ {i} (\ alpha _ {i}) - L (\ zeta _ {1}, \ ldots, \ zeta _ {s}, {\ dot {q}} _ {1} (\ alpha _ {1}), \ ldots , {\ dot {q}} _ {n} (\ alpha _ {n}), {\ dot {\ zeta}} _ {1}, \ ldots, {\ dot {\ zeta}} _ {s}, t) \ ,,}$

Den 2 n Hamiltonian ligning i de cykliske koordinater forsvinder automatisk,

${\ displaystyle {\ dot {q}} _ {i} = {\ frac {\ partial R} {\ partial \ alpha _ {i}}} = f_ {i} (\ zeta _ {1} (t), \ ldots, \ zeta _ {s} (t), {\ dot {\ zeta}} _ {1} (t), \ ldots, {\ dot {\ zeta}} _ {s} (t), \ alpha _ {1}, \ ldots, \ alpha _ {n}, t) \ ,, \ quad {\ dot {p}} _ {i} = - {\ frac {\ partial R} {\ partial q_ {i} }} = 0 \ ,,}$

og s Lagrangian ligninger er i de ikke-cykliske koordinater

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial R} {\ partial {\ dot {\ zeta}} _ {j}}} = {\ frac {\ partial R} {\ partial \ zeta _ {j}}},.}$

Således er problemet reduceret til at løse Lagrangian-ligningerne i de ikke-cykliske koordinater, idet fordelen ved, at Hamilton-ligningerne rent fjerner de cykliske koordinater. Ved hjælp af disse løsninger kan ligningerne for integreres til beregning . ${\ displaystyle {\ dot {q}} _ {i}}$${\ displaystyle q_ {i} (t)}$

Hvis vi er interesserede i, hvordan de cykliske koordinater ændrer sig med tiden, kan ligningerne for de generaliserede hastigheder svarende til de cykliske koordinater integreres.

Eksempler

Rouths procedure garanterer ikke, at bevægelsesligningerne vil være enkle, men det vil føre til færre ligninger.

Centralt potentiale i sfæriske koordinater

En generel klasse af mekaniske systemer med cykliske koordinater er dem med centrale potentialer , fordi potentialer i denne form kun har afhængighed af radiale adskillelser og ingen afhængighed af vinkler.

Overvej en partikel med masse m under indflydelse af et centralt potential V ( r ) i sfæriske polære koordinater ( r , θ , φ )

${\ displaystyle L (r, {\ dot {r}}, \ theta, {\ dot {\ theta}}, {\ dot {\ phi}}) = {\ frac {m} {2}} ({\ prik {r}} ^ {2} + {r} ^ {2} {\ dot {\ theta}} ^ {2} + r ^ {2} \ sin ^ {2} \ theta {\ dot {\ phi} } ^ {2}) - V (r) \ ,.}$

Bemærk φ er cyklisk, fordi den ikke vises i Lagrangian. Momentet konjugeret til φ er konstant

${\ displaystyle p _ {\ phi} = {\ frac {\ partial L} {\ partial {\ dot {\ phi}}}} = mr ^ {2} \ sin ^ {2} \ theta {\ dot {\ phi }} \ ,,}$

hvor r og dφ / dt kan variere med tiden, men vinkelmomentet p _φ er konstant. Routhian kan tages for at være

${\ displaystyle {\ begin {align} R (r, {\ dot {r}}, \ theta, {\ dot {\ theta}}) & = p _ {\ phi} {\ dot {\ phi}} - L \\ & = p _ {\ phi} {\ dot {\ phi}} - {\ frac {m} {2}} {\ dot {r}} ^ {2} - {\ frac {m} {2}} r ^ {2} {\ dot {\ theta}} ^ {2} - {\ frac {p _ {\ phi} {\ dot {\ phi}}} {2}} + V (r) \\ & = { \ frac {p _ {\ phi} {\ dot {\ phi}}} {2}} - {\ frac {m} {2}} {\ dot {r}} ^ {2} - {\ frac {m} {2}} r ^ {2} {\ dot {\ theta}} ^ {2} + V (r) \\ & = {\ frac {p _ {\ phi} ^ {2}} {2mr ^ {2} \ sin ^ {2} \ theta}} - {\ frac {m} {2}} {\ dot {r}} ^ {2} - {\ frac {m} {2}} r ^ {2} {\ prik {\ theta}} ^ {2} + V (r) \,. \ slut {justeret}}}$

Vi kan løse for r og θ ved hjælp af Lagrange's ligninger og behøver ikke at løse for φ da det elimineres af Hamiltonians ligninger. Den r ligning er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial R} {\ partial {\ dot {r}}}} = {\ frac {\ partial R} {\ partial r}} \ quad \ Rightarrow \ quad -m {\ ddot {r}} = - {\ frac {p _ {\ phi} ^ {2}} {mr ^ {3} \ sin ^ {2} \ theta}} - mr {\ dot {\ theta}} ^ {2} + {\ frac {\ partial V} {\ partial r}} \ ,,}$

og ligningen θ er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial R} {\ partial {\ dot {\ theta}}}} = {\ frac {\ partial R} {\ partial \ theta}} \ quad \ Rightarrow \ quad -m (2r {\ dot {r}} {\ dot {\ theta}} + r ^ {2} {\ ddot {\ theta}}) = - {\ frac {p _ {\ phi } ^ {2} \ cos \ theta} {mr ^ {2} \ sin ^ {3} \ theta}} \ ,.}$

Den routhiske tilgang har opnået to koblede ikke-lineære ligninger. I modsætning hertil fører Lagrangian-tilgangen til tre ikke-lineære koblede ligninger, der blandes første og anden gang afledte af φ i dem alle på trods af dets fravær fra Lagrangian.

Den r ligning er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {r}}}} = {\ frac {\ partial L} {\ partial r}} \ quad \ Rightarrow \ quad m {\ ddot {r}} = mr {\ dot {\ theta}} ^ {2} + mr \ sin ^ {2} \ theta {\ dot {\ phi}} ^ {2} - { \ frac {\ partial V} {\ partial r}} \ ,,}$

den θ ligning er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {\ theta}}}} = {\ frac {\ partial L} {\ partial \ theta}} \ quad \ Rightarrow \ quad 2r {\ dot {r}} {\ dot {\ theta}} + r ^ {2} {\ ddot {\ theta}} = r ^ {2} \ sin \ theta \ cos \ theta {\ dot {\ phi}} ^ {2} \ ,,}$

den φ ligning er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {\ phi}}}} = {\ frac {\ partial L} {\ partial \ phi}} \ quad \ Rightarrow \ quad 2r {\ dot {r}} \ sin ^ {2} \ theta {\ dot {\ phi}} + 2r ^ {2} \ sin \ theta \ cos \ theta {\ dot {\ theta }} {\ dot {\ phi}} + r ^ {2} \ sin ^ {2} \ theta {\ ddot {\ phi}} = 0 \ ,.}$

Symmetriske mekaniske systemer

Sfærisk pendul

Sfærisk pendul: vinkler og hastigheder.

Overvej det sfæriske pendul , en masse m (kendt som en "pendulbob"), der er fastgjort til en stiv stang med længden l af ubetydelig masse underlagt et lokalt tyngdefelt g . Systemet roterer med en vinkelhastighed dφ / dt, som ikke er konstant. Vinklen mellem stangen og lodret er θ og er ikke konstant.

Lagrangian er

${\ displaystyle L (\ theta, {\ dot {\ theta}}, {\ dot {\ phi}}) = {\ frac {m \ ell ^ {2}} {2}} ({\ dot {\ theta }} ^ {2} + \ sin ^ {2} \ theta {\ dot {\ phi}} ^ {2}) + mg \ ell \ cos \ theta \ ,,}$

og φ er den cykliske koordinat for systemet med konstant momentum

${\ displaystyle p _ {\ phi} = {\ frac {\ partial L} {\ partial {\ dot {\ phi}}}} = m \ ell ^ {2} \ sin ^ {2} \ theta {\ dot { \ phi}} \.}$

hvilket igen er fysisk vinkelmomentet i systemet omkring det lodrette. Vinklen θ og vinkelhastigheden dφ / dt varierer med tiden, men vinkelmomentet er konstant. Den routhiske er

${\ displaystyle {\ begin {align} R (\ theta, {\ dot {\ theta}}) & = p _ {\ phi} {\ dot {\ phi}} - L \\ & = p _ {\ phi} { \ dot {\ phi}} - {\ frac {m \ ell ^ {2}} {2}} {\ dot {\ theta}} ^ {2} - {\ frac {p _ {\ phi} {\ dot { \ phi}}} {2}} - mg \ ell \ cos \ theta \\ & = {\ frac {p _ {\ phi} {\ dot {\ phi}}} {2}} - {\ frac {m \ ell ^ {2}} {2}} {\ dot {\ theta}} ^ {2} -mg \ ell \ cos \ theta \\ & = {\ frac {p _ {\ phi} ^ {2}} {2m \ ell ^ {2} \ sin ^ {2} \ theta}} - {\ frac {m \ ell ^ {2}} {2}} {\ dot {\ theta}} ^ {2} -mg \ ell \ cos \ theta \ end {align}}}$

Den θ ligning er fundet fra de Lagrange ligninger

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial R} {\ partial {\ dot {\ theta}}}} = {\ frac {\ partial R} {\ partial \ theta}} \ quad \ Rightarrow \ quad -m \ ell ^ {2} {\ ddot {\ theta}} = - {\ frac {p _ {\ phi} ^ {2} \ cos \ theta} {m \ ell ^ {2} \ sin ^ {3} \ theta}} + mg \ ell \ sin \ theta \ ,,}$

eller forenkling ved at introducere konstanterne

${\ displaystyle a = {\ frac {p _ {\ phi} ^ {2}} {m ^ {2} \ ell ^ {4}}} \ ,, \ quad b = {\ frac {g} {\ ell} } \ ,,}$

giver

${\ displaystyle {\ ddot {\ theta}} = a {\ frac {\ cos \ theta} {\ sin ^ {3} \ theta}} - b \ sin \ theta \ ,.}$

Denne ligning ligner den enkle ikke-lineære pendulligning , fordi den kan svinge gennem den lodrette akse med et yderligere udtryk for at tage højde for rotationen omkring den lodrette akse (konstanten a er relateret til vinkelmomentet p _φ ).

Ved at anvende den Lagrangiske tilgang er der to ikke-lineære koblede ligninger at løse.

Den θ ligning er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {\ theta}}}} = {\ frac {\ partial L} {\ partial \ theta}} \ quad \ Rightarrow \ quad m \ ell ^ {2} {\ ddot {\ theta}} = m \ ell ^ {2} \ sin \ theta \ cos \ theta {\ dot {\ phi}} ^ {2} - mg \ ell \ sin \ theta \ ,,}$

og ligningen φ er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {\ phi}}}} = {\ frac {\ partial L} {\ partial \ phi}} \ quad \ Rightarrow \ quad 2 \ sin \ theta \ cos \ theta {\ dot {\ theta}} {\ dot {\ phi}} + \ sin ^ {2} \ theta {\ ddot {\ phi}} = 0 \ ,.}$

Kraftig symmetrisk top

Tung symmetrisk top med hensyn til Euler-vinklerne.

Den tunge symmetriske top af masse M har Lagrangian

${\ displaystyle L (\ theta, {\ dot {\ theta}}, {\ dot {\ psi}}, {\ dot {\ phi}}) = {\ frac {I_ {1}} {2}} ( {\ dot {\ theta}} ^ {2} + {\ dot {\ phi}} ^ {2} \ sin ^ {2} \ theta) + {\ frac {I_ {3}} {2}} ({ \ dot {\ psi}} ^ {2} + {\ dot {\ phi}} ^ {2} \ cos ^ {2} \ theta) + I_ {3} {\ dot {\ psi}} {\ dot { \ phi}} \ cos \ theta -Mg \ ell \ cos \ theta}$

hvor ψ , φ , θ er Euler-vinklerne , θ er vinklen mellem den lodrette z- akse og topens z ′ -aks, ψ er rotationen af ​​toppen omkring sin egen z ′ -aks, og φ azimuthal af top s z ' -aksen omkring den lodrette z -aksen. De vigtigste inertimomenter er I ₁ om topens egen x ' akse, I ₂ om topens egne y ' akser og I ₃ om topens egen z ' akse. Da toppen er symmetrisk omkring sin z ' -aksen, I ₁ = I ₂ . Her den enkle forhold til lokal gravitationel potentiel energi V = Mgl cos θ anvendes, hvor g er tyngdeaccelerationen, og centrum af massen af toppen er en afstand l fra dens spids langs dens z ' -aksen.

Vinklerne ψ , φ er cykliske. De konstante momenta er henholdsvis topens vinkelmomenter omkring dens akse og dets presession omkring henholdsvis lodret:

${\ displaystyle p _ {\ psi} = {\ frac {\ partial L} {\ partial {\ dot {\ psi}}}} = I_ {3} {\ dot {\ psi}} + I_ {3} {\ prik {\ phi}} \ cos \ theta}$

${\ displaystyle p _ {\ phi} = {\ frac {\ partial L} {\ partial {\ dot {\ phi}}}} = {\ dot {\ phi}} (I_ {1} \ sin ^ {2} \ theta + I_ {3} \ cos ^ {2} \ theta) + I_ {3} {\ dot {\ psi}} \ cos \ theta}$

Fra disse fjernes dψ / dt :

${\ displaystyle p _ {\ phi} -p _ {\ psi} \ cos \ theta = I_ {1} {\ dot {\ phi}} \ sin ^ {2} \ theta}$

vi har

${\ displaystyle {\ dot {\ phi}} = {\ frac {p _ {\ phi} -p _ {\ psi} \ cos \ theta} {I_ {1} \ sin ^ {2} \ theta}} \ ,, }$

og for at eliminere dφ / dt skal du erstatte dette resultat i p _ψ og løse for dψ / dt at finde

${\ displaystyle {\ dot {\ psi}} = {\ frac {p _ {\ psi}} {I_ {3}}} - \ cos \ theta \ left ({\ frac {p _ {\ phi} -p _ {\ psi} \ cos \ theta} {I_ {1} \ sin ^ {2} \ theta}} \ højre) \ ,.}$

Routhian kan tages for at være

${\ displaystyle R (\ theta, {\ dot {\ theta}}) = p _ {\ psi} {\ dot {\ psi}} + p _ {\ phi} {\ dot {\ phi}} - L = {\ frac {1} {2}} (p _ {\ psi} {\ dot {\ psi}} + p _ {\ phi} {\ dot {\ phi}}) - {\ frac {I_ {1} {\ dot { \ theta}} ^ {2}} {2}} + Mg \ ell \ cos \ theta}$

og siden

${\ displaystyle {\ frac {p _ {\ phi} {\ dot {\ phi}}} {2}} = {\ frac {p _ {\ phi} ^ {2}} {2I_ {1} \ sin ^ {2 } \ theta}} - {\ frac {p _ {\ psi} p _ {\ phi} \ cos \ theta} {2I_ {1} \ sin ^ {2} \ theta}} \ ,,}$

${\ displaystyle {\ frac {p _ {\ psi} {\ dot {\ psi}}} {2}} = {\ frac {p _ {\ psi} ^ {2}} {2I_ {3}}} - {\ frac {p _ {\ psi} p _ {\ phi} \ cos \ theta} {2I_ {1} \ sin ^ {2} \ theta}} + {\ frac {p _ {\ psi} ^ {2} \ cos ^ { 2} \ theta} {2I_ {1} \ sin ^ {2} \ theta}}}$

vi har

${\ displaystyle R = {\ frac {p _ {\ psi} ^ {2}} {2I_ {3}}} + {\ frac {p _ {\ psi} ^ {2} \ cos ^ {2} \ theta} { 2I_ {1} \ sin ^ {2} \ theta}} + {\ frac {p _ {\ phi} ^ {2}} {2I_ {1} \ sin ^ {2} \ theta}} - {\ frac {p_ {\ psi} p _ {\ phi} \ cos \ theta} {I_ {1} \ sin ^ {2} \ theta}} - {\ frac {I_ {1} {\ dot {\ theta}} ^ {2} } {2}} + Mg \ ell \ cos \ theta \ ,.}$

Det første udtryk er konstant og kan ignoreres, da kun derivaterne af R vil komme ind i bevægelsesligningerne. Den forenklede Routhian uden tab af information er således

${\ displaystyle R = {\ frac {1} {2I_ {1} \ sin ^ {2} \ theta}} \ left [p _ {\ psi} ^ {2} \ cos ^ {2} \ theta + p _ {\ phi} ^ {2} - {\ frac {p _ {\ psi} p _ {\ phi}} {2}} \ cos \ theta \ right] - {\ frac {I_ {1} {\ dot {\ theta}} ^ {2}} {2}} + Mg \ ell \ cos \ theta}$

Bevægelsesligningen for θ er ved direkte beregning

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial R} {\ partial {\ dot {\ theta}}}} = {\ frac {\ partial R} {\ partial \ theta}} \ quad \ Rightarrow \ quad}$

${\ displaystyle -I_ {1} {\ ddot {\ theta}} = - {\ frac {\ cos \ theta} {I_ {1} \ sin ^ {3} \ theta}} \ venstre [p _ {\ psi} ^ {2} \ cos ^ {2} \ theta + p _ {\ phi} ^ {2} - {\ frac {p _ {\ psi} p _ {\ phi}} {2}} \ cos \ theta \ right] + {\ frac {1} {2I_ {1} \ sin ^ {2} \ theta}} \ venstre [-2p _ {\ psi} ^ {2} \ cos \ theta \ sin \ theta + {\ frac {p _ {\ psi} p _ {\ phi}} {2}} \ sin \ theta \ right] -Mg \ ell \ sin \ theta \ ,,}$

eller ved at introducere konstanterne

${\ displaystyle a = {\ frac {p _ {\ psi} ^ {2}} {I_ {1} ^ {2}}} \ ,, \ quad b = {\ frac {p _ {\ phi} ^ {2} } {I_ {1} ^ {2}}} \ ,, \ quad c = {\ frac {p _ {\ psi} p _ {\ phi}} {2I_ {1} ^ {2}}} \ ,, \ quad k = {\ frac {Mg \ ell} {I_ {1}}} \ ,,}$

en enklere form af ligningen opnås

${\ displaystyle {\ ddot {\ theta}} = {\ frac {\ cos \ theta} {\ sin ^ {3} \ theta}} (a \ cos ^ {2} \ theta + bc \ cos \ theta) + {\ frac {1} {2 \ sin \ theta}} (2a \ cos \ theta -c) + k \ sin \ theta \ ,.}$

Selvom ligningen er meget ikke-lineær, er der kun en ligning at løse for, den blev opnået direkte, og de cykliske koordinater er ikke involveret.

I modsætning hertil fører Lagrangian-tilgangen til tre ikke-lineære koblede ligninger at løse, på trods af fraværet af koordinaterne ψ og φ i Lagrangian.

Den θ ligning er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {\ theta}}}} = {\ frac {\ partial L} {\ partial \ theta}} \ quad \ Rightarrow \ quad I_ {1} {\ ddot {\ theta}} = (I_ {1} -I_ {3}) {\ dot {\ phi}} ^ {2} \ sin \ theta \ cos \ theta -I_ {3} {\ dot {\ psi}} {\ dot {\ phi}} \ sin \ theta + Mg \ ell \ sin \ theta \ ,,}$

den ψ ligning er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {\ psi}}}} = {\ frac {\ partial L} {\ partial \ psi}} \ quad \ Rightarrow \ quad {\ ddot {\ psi}} + {\ ddot {\ phi}} \ cos \ theta - {\ dot {\ phi}} {\ dot {\ theta}} \ sin \ theta = 0 \ ,,}$

og ligningen φ er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {\ phi}}}} = {\ frac {\ partial L} {\ partial \ phi}} \ quad \ Rightarrow \ quad {\ ddot {\ phi}} (I_ {1} \ sin ^ {2} \ theta + I_ {3} \ cos ^ {2} \ theta) + {\ dot {\ phi}} (I_ {1} -I_ {3}) 2 \ sin \ theta \ cos \ theta {\ dot {\ theta}} + I_ {3} {\ ddot {\ psi}} \ cos \ theta -I_ {3} {\ dot {\ psi}} \ sin \ theta {\ dot {\ theta}} = 0 \ ,,}$

Hastighedsafhængige potentialer

Klassisk ladet partikel i et ensartet magnetfelt

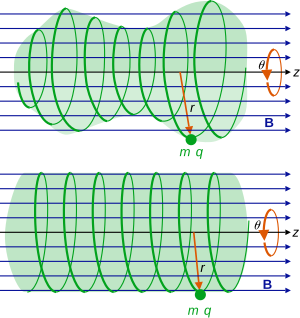
Klassisk ladet partikel i ensartet B- felt ved hjælp af cylindriske koordinater. Top: Hvis den radiale koordinat r og vinkelhastigheden dθ / dt varierer, er banen en helikoid med varierende radius, men ensartet bevægelse i z- retningen. Nederst: Konstant r og dθ / dt betyder en helikoid med konstant radius.

Overvej en klassisk ladet partikel med masse m og elektrisk ladning q i en statisk (tidsuafhængige) ensartet (konstant under space) magnetfelt B . Lagrangian for en ladet partikel i et generelt elektromagnetisk felt givet af det magnetiske potentiale A og det elektriske potentiale er ${\ displaystyle \ phi}$

${\ displaystyle L = {\ frac {m} {2}} {\ dot {\ mathbf {r}}} ^ {2} -q \ phi + q {\ dot {\ mathbf {r}}} \ cdot \ mathbf {A} \ ,,}$

Det er praktisk at bruge cylindriske koordinater ( r , θ , z ) , således at

${\ displaystyle {\ dot {\ mathbf {r}}} = \ mathbf {v} = (v_ {r}, v _ {\ theta}, v_ {z}) = ({\ dot {r}}, r { \ dot {\ theta}}, {\ dot {z}}) \ ,,}$

${\ displaystyle \ mathbf {B} = (B_ {r}, B _ {\ theta}, B_ {z}) = (0,0, B) \ ,.}$

I dette tilfælde uden noget elektrisk felt er det elektriske potentiale nul , og vi kan vælge den aksiale måler til det magnetiske potentiale ${\ displaystyle \ phi = 0}$

${\ displaystyle \ mathbf {A} = {\ frac {1} {2}} \ mathbf {B} \ times \ mathbf {r} \ quad \ Rightarrow \ quad \ mathbf {A} = (A_ {r}, A_ {\ theta}, A_ {z}) = (0, Br / 2,0) \ ,,}$

og Lagrangian er

${\ displaystyle L (r, {\ dot {r}}, {\ dot {\ theta}}, {\ dot {z}}) = {\ frac {m} {2}} ({\ dot {r} } ^ {2} + r ^ {2} {\ dot {\ theta}} ^ {2} + {\ dot {z}} ^ {2}) + {\ frac {qBr ^ {2} {\ dot { \ theta}}} {2}} \ ,.}$

Bemærk dette potentiale har en effektiv cylindrisk symmetri (selvom det også har vinkelhastighedsafhængighed), da den eneste rumlige afhængighed er af den radiale længde fra en imaginær cylinderakse.

Der er to cykliske koordinater, θ og z . Det kanoniske momenta konjugeret til θ og z er konstanterne

${\ displaystyle p _ {\ theta} = {\ frac {\ partial L} {\ partial {\ dot {\ theta}}}} = mr ^ {2} {\ dot {\ theta}} + {\ frac {qBr ^ {2}} {2}} \ ,, \ quad p_ {z} = {\ frac {\ partial L} {\ partial {\ dot {z}}}} = m {\ dot {z}} \, ,}$

så hastighederne er

${\ displaystyle {\ dot {\ theta}} = {\ frac {1} {mr ^ {2}}} \ left (p _ {\ theta} - {\ frac {qBr ^ {2}} {2}} \ højre) \ ,, \ quad {\ dot {z}} = {\ frac {p_ {z}} {m}} \ ,.}$

Vinkelmomentet omkring z- aksen er ikke p _θ , men størrelsen mr ² dθ / dt , som ikke bevares på grund af bidraget fra magnetfeltet. Det kanoniske momentum p _θ er den bevarede mængde. Det er stadig tilfældet, at p _z er det lineære eller translationelle momentum langs z- aksen, som også er bevaret.

Den radiale komponent r og vinkelhastigheden dθ / dt kan variere med tiden, men p _θ er konstant, og da p _z er konstant, følger dz / dt konstant. Routhian kan tage form

${\ displaystyle {\ begin {align} R (r, {\ dot {r}}) & = p _ {\ theta} {\ dot {\ theta}} + p_ {z} {\ dot {z}} - L \\ & = p _ {\ theta} {\ dot {\ theta}} + p_ {z} {\ dot {z}} - {\ frac {m} {2}} {\ dot {r}} ^ {2 } - {\ frac {p _ {\ theta} {\ dot {\ theta}}} {2}} - {\ frac {p_ {z} {\ dot {z}}} {2}} - {\ frac { 1} {2}} qBr ^ {2} {\ dot {\ theta}} \\ [6pt] & = (p _ {\ theta} -qBr ^ {2}) {\ frac {\ dot {\ theta}} {2}} - {\ frac {m} {2}} {\ dot {r}} ^ {2} + {\ frac {p_ {z} {\ dot {z}}} {2}} \\ [ 6pt] & = {\ frac {1} {2mr ^ {2}}} \ venstre (p _ {\ theta} -qBr ^ {2} \ højre) \ venstre (p _ {\ theta} - {\ frac {qBr ^ {2}} {2}} \ right) - {\ frac {m} {2}} {\ dot {r}} ^ {2} + {\ frac {p_ {z} ^ {2}} {2m} } \\ [6pt] & = {\ frac {1} {2mr ^ {2}}} \ left (p _ {\ theta} ^ {2} - {\ frac {3} {2}} qBr ^ {2} + {\ frac {(qB) ^ {2} r ^ {4}} {2}} \ right) - {\ frac {m} {2}} {\ dot {r}} ^ {2} \ end { justeret}}}$

hvor i sidste linje, den p _z ² /2 m sigt er en konstant og kan ignoreres uden tab af kontinuitet. Hamilton-ligningerne for θ og z forsvinder automatisk og behøver ikke løses. Lagrangians ligning i r

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial R} {\ partial {\ dot {r}}}} = {\ frac {\ partial R} {\ partial r}}}$

er ved direkte beregning

${\ displaystyle -m {\ ddot {r}} = {\ frac {1} {2m}} \ venstre [{\ frac {-2} {r ^ {3}}} \ venstre (p _ {\ theta} ^ {2} - {\ frac {3} {2}} qBr ^ {2} + {\ frac {(qB) ^ {2} r ^ {4}} {2}} \ højre) + {\ frac {1 } {r ^ {2}}} (- 3qBr + 2 (qB) ^ {2} r ^ {3}) \ højre] \ ,,}$

som efter indsamling af vilkår er

${\ displaystyle m {\ ddot {r}} = {\ frac {1} {2m}} \ venstre [{\ frac {2p _ {\ theta} ^ {2}} {r ^ {3}}} - (qB ) ^ {2} r \ right] \ ,,}$

og forenkling yderligere ved at introducere konstanterne

${\ displaystyle a = {\ frac {p _ {\ theta} ^ {2}} {m ^ {2}}} \ ,, \ quad b = - {\ frac {(qB) ^ {2}} {2m ^ {2}}} \ ,,}$

differentialligningen er

${\ displaystyle {\ ddot {r}} = {\ frac {a} {r ^ {3}}} + br}$

For at se, hvordan z ændres med tiden, skal du integrere momenta-udtrykket for p _z ovenfor

${\ displaystyle z = {\ frac {p_ {z}} {m}} t + c_ {z} \ ,,}$

hvor c _z er en vilkårlig konstant, skal den oprindelige værdi af z specificeres under de oprindelige betingelser .

Partiklens bevægelse i dette system er heloidformet , med den aksiale bevægelse ensartet (konstant), men de radiale og vinklede komponenter varierer i en spiral i henhold til den ovennævnte bevægelsesligning. De indledende betingelser på r , dr / dt , θ , dθ / dt , vil afgøre, om partikelens bane har en konstant r eller varierende r . Hvis oprindeligt r ikke er nul, men dr / dt = 0 , mens θ og dθ / dt er vilkårlige, har partikelens starthastighed ingen radial komponent, r er konstant, så bevægelsen vil være i en perfekt helix. Hvis r er konstant, er vinkelhastigheden også konstant i henhold til den konserverede p _θ .

Med den Lagrangiske tilgang ville ligningen for r omfatte dθ / dt, som skal elimineres, og der ville være ligninger for θ og z at løse.

Den r ligning er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {r}}}} = {\ frac {\ partial L} {\ partial r}} \ quad \ Rightarrow \ quad m {\ ddot {r}} = mr {\ dot {\ theta}} ^ {2} + qBr {\ dot {\ theta}} \ ,,}$

den θ ligning er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {\ theta}}}} = {\ frac {\ partial L} {\ partial \ theta}} \ quad \ Rightarrow \ quad m (2r {\ dot {r}} {\ dot {\ theta}} + r ^ {2} {\ ddot {\ theta}}) + qBr {\ dot {r}} = 0 \ ,,}$

og z ligningen er

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {z}}}} = {\ frac {\ partial L} {\ partial z}} \ quad \ Rightarrow \ quad m {\ ddot {z}} = 0 \ ,.}$

Den z ligning er trivielt at integrere, men r og Ø ligninger er ikke i alle tilfælde den tid derivater blandes i alle ligningerne og skal fjernes.

Se også

• Beregning af variationer
• Faseplads
• Konfigurationsplads
• Problem med mange legemer
• Stiv kropsmekanik

Fodnoter

Bemærkninger

Referencer

• Landau, LD ; Lifshitz, EM (15. januar 1976). Mekanik (3. udgave). Butterworth Heinemann. s. 134. ISBN   9780750628969 .
• Hånd, LN; Finch, JD (13. november 1998). Analytisk mekanik (2. udgave). Cambridge University Press. s. 23. ISBN   9780521575720 .
• Kibble, TWB; Berkshire, FH (2004). Klassisk mekanik (5. udgave). Imperial College Press. s. 236. ISBN   9781860944352 .
• Goldstein, Herbert (1980). Klassisk mekanik (2. udgave). San Francisco, Californien: Addison Wesley. s. 352–353. ISBN   0201029189 .
• Goldstein, Herbert ; Poole, Charles P., Jr .; Safko, John L. (2002). Klassisk mekanik (3. udgave). San Francisco, Californien: Addison Wesley. s. 347–349. ISBN   0-201-65702-3 .