Tangentlinjer til cirkler - Tangent lines to circles

I den euklidiske plangeometri er en tangentlinje til en cirkel en linje, der berører cirklen på præcis et tidspunkt og aldrig kommer ind i cirkelens indre. Tangentlinjer til cirkler danner genstand for flere sætninger og spiller en vigtig rolle i mange geometriske konstruktioner og beviser . Da tangentlinjen til en cirkel i et punkt P er vinkelret på radius til dette punkt, involverer sætninger, der involverer tangentlinjer, ofte radiale linjer og ortogonale cirkler.

Tangentlinjer til en cirkel

En tangent t til en cirkel C skærer cirklen ved et enkelt punkt T . Til sammenligning, sekant skærer en cirkel på to punkter, mens en anden linje kan ikke skærer en cirkel på alle. Denne egenskab ved tangentlinjer bevares under mange geometriske transformationer , såsom skaleringer , rotation , oversættelser , inversioner og kortfremskrivninger . I fagsprog ændrer disse transformationer ikke forekomststrukturen for tangentlinjen og cirklen, selvom linjen og cirklen kan blive deformeret.

Radius af en cirkel er vinkelret på tangentlinjen gennem dens endepunkt på cirkelens omkreds. Omvendt er vinkelret på en radius gennem det samme endepunkt en tangentlinje. Den resulterende geometriske figur af cirkel og tangentlinje har en refleksionssymmetri omkring radiusens akse.

Ved power-of-a-point sætningen er produktet af længder PM · PN for enhver stråle PMN lig med kvadratet af PT, længden af ​​tangentlinjesegmentet (rød).

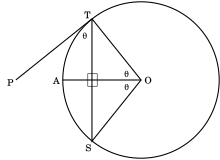
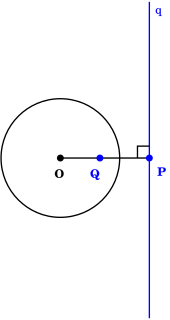
Ingen tangentlinje kan trækkes gennem et punkt inden for en cirkel, da enhver sådan linje skal være en sekant linje. Men to kan tangent linjer trækkes til en cirkel fra et punkt P ydersiden af cirklen. Den geometriske figur af en cirkel og begge tangentlinjer har ligeledes en refleksionssymmetri om den radiale akse, der forbinder P med cirkelens centerpunkt O. Således er længderne af segmenterne fra P til de to tangentpunkter ens. Ved sekant-tangenten teorem , kvadratet af denne tangent længde er lig med magt punktet P i cirklen C . Denne magt er lig med produktet af afstande fra P til enhver to skæringspunkter af cirklen med en sekant linje gennem P .

Vinklen θ mellem en akkord og en tangent er den halve bue, der tilhører akkorden.

Tangentlinjen t og tangentpunktet T har et konjugeret forhold til hinanden, som er blevet generaliseret til ideen om polpunkter og polære linjer . Det samme gensidige forhold eksisterer mellem et punkt P uden for cirklen og den sekantiske linje, der forbinder dets to tangenspunkter.

Hvis et punkt P er udvendigt for en cirkel med centrum O, og hvis tangentlinjerne fra P berører cirklen ved punkterne T og S, er ∠TPS og ∠TOS supplerende (sum til 180 °).

Hvis en akkord TM trækkes fra tangenspunktet T på det udvendige punkt P og ∠PTM ≤ 90 °, så er ∠PTM = (1/2) ∠TOM.

Ligning af tangentlinjen med koordinat

Antag, at cirkelens ligning er med centrum ved . Så tangentlinjen af cirklen ved IS ${\ displaystyle (xa)^{2}+(yb)^{2} = r^{2}}$${\ displaystyle (a, b)}$${\ displaystyle (x_ {1}, y_ {1})}$

${\ displaystyle (x-x_ {1}) (x_ {1} -a)+(y-y_ {1}) (y_ {1} -b) = 0}$

Dette kan bevises ved at tage den implicitte afledning af cirklen.

Kompas og opretstående konstruktioner

Det er relativt ligetil at konstruere en linje t, der tangerer en cirkel i et punkt T på cirkelens omkreds:

• En linje a er trukket fra O , midten af ​​cirklen, gennem radialpunktet T ;
• Linjen t er den vinkelrette linje til a .

Konstruktion af en tangent til en given cirkel (sort) fra et givet udvendigt punkt (P).

Thales 'sætning kan bruges til at konstruere tangentlinjerne til et punkt P uden for cirklen C :

• En cirkel tegnes centreret på midtpunktet af linjestykke OP, som har en diameter OP, hvor O er igen centrum af cirklen C .
• Skæringspunkterne T ₁ og T ₂ i cirklen C og den nye cirkel er tangentpunkterne for linjer, der passerer gennem P , af følgende argument.

Linjesegmenterne OT ₁ og OT ₂ er radier af cirklen C ; da begge er indskrevet i en halvcirkel, er de vinkelret på henholdsvis linjesegmenterne PT ₁ og PT ₂ . Men kun en tangentlinje er vinkelret på den radiale linje. Dermed de to linjer fra P og passerer gennem T ₁ og T ₂ tangerer cirklen C .

En anden metode til at konstruere tangentlinjerne til et punkt P uden for cirklen ved hjælp af kun en straightedge :

• Tegn tre forskellige linjer gennem det givne punkt P, der skærer cirklen to gange.
• Lad være de seks skæringspunkter, med det samme bogstav svarende til den samme linje og indekset 1 svarende til punktet tættere på P.${\ displaystyle A_ {1}, A_ {2}, B_ {1}, B_ {2}, C_ {1}, C_ {2}}$
• Lad D være det punkt, hvor linjerne og skærer hinanden,${\ displaystyle A_ {1} B_ {2}}$${\ displaystyle A_ {2} B_ {1}}$
• Tilsvarende E for linjerne og .${\ displaystyle B_ {1} C_ {2}}$${\ displaystyle B_ {2} C_ {1}}$
• Tegn en linje gennem D og E.
• Denne linje møder cirklen på to punkter, F og G.
• Tangenterne er linjerne PF og PG.

Med analytisk geometri

Lad være et punkt i cirklen med ligning . Tangenten at har ligning , fordi den ligger på begge kurver og er en normal vektor af linjen. Tangenten skærer x-aksen i punkt med . ${\ displaystyle P = (a, b)}$${\ displaystyle x^{2}+y^{2} = r^{2}}$${\ displaystyle P}$${\ displaystyle ax+by = r^{2}}$${\ displaystyle P}$${\ displaystyle {\ vec {OP}} = (a, b)^{T}}$${\ displaystyle P_ {0} = (x_ {0}, 0)}$${\ displaystyle ax_ {0} = r^{2}}$

Tangenter gennem et punkt

Omvendt, hvis man starter med punkt , end de to tangenter igennem møder cirklen på de to punkter med ${\ displaystyle P_ {0} = (x_ {0}, 0)}$${\ displaystyle P_ {0}}$${\ displaystyle P_ {1/2} = (a, b _ {\ pm})}$

${\ displaystyle a = {\ frac {r^{2}} {x_ {0}}}, \ qquad b _ {\ pm} = \ pm {\ sqrt {r^{2} -a^{2}}} = \ pm {\ frac {r} {x_ {0}}} {\ sqrt {x_ {0}^{2} -r^{2}}} \ quad}$. Skrevet i vektorform:

${\ displaystyle {\ binom {a} {b _ {\ pm}}} = {\ frac {r^{2}} {x_ {0}}} {\ binom {1} {0}} \ pm {\ frac {r} {x_ {0}}} {\ sqrt {x_ {0}^{2} -r^{2}}} {\ binom {0} {1}} \.}$

Hvis punktet ikke ligger på x-aksen: I vektorformen erstattes man med afstanden og enhedsbasisvektorerne med de ortogonale enhedsvektorer . Derefter berører tangenterne gennem punktet cirklen ved punkterne ${\ displaystyle P_ {0} = (x_ {0}, y_ {0})}$${\ displaystyle x_ {0}}$${\ displaystyle \ d_ {0} = {\ sqrt {x_ {0}^{2}+y_ {0}^{2}}} \}$${\ displaystyle \ {\ vec {e}} _ {1} = {\ frac {1} {d_ {0}}} {\ binom {x_ {0}} {y_ {0}}}, \ {\ vec {e}} _ {2} = {\ frac {1} {d_ {0}}} {\ binom {-y_ {0}} {x_ {0}}} \}$${\ displaystyle P_ {0}}$

${\ displaystyle {\ binom {x_ {1/2}} {y_ {1/2}}} = {\ frac {r^{2}} {d_ {0}^{2}}} {\ binom {x_ {0}} {y_ {0}}} \ pm {\ frac {r} {d_ {0}^{2}}} {\ sqrt {d_ {0}^{2} -r^{2}}} {\ binom {-y_ {0}} {x_ {0}}} \.}$

For der findes ingen tangenter. For punkt ligger på cirklen, og der er kun en tangent med ligning . I tilfælde af er der 2 tangenter med ligninger . ${\ displaystyle d_ {0} <r}$
${\ displaystyle d_ {0} = r}$${\ displaystyle P_ {0}}$${\ displaystyle x_ {0} x+y_ {0} y = r^{2}}$
${\ displaystyle d_ {0}> r}$${\ displaystyle \ x_ {1} x+y_ {1} y = r^{2}, \ x_ {2} x+y_ {2} y = r^{2}}$

Forhold til cirkelinversion : Ligning beskriver cirkelens inversion af punkt . ${\ displaystyle ax_ {0} = r^{2}}$${\ displaystyle (x_ {0}, 0)}$

Forhold til pol og polar : Punktets polar har ligning . ${\ displaystyle (x_ {0}, 0)}$${\ displaystyle xx_ {0} = r^{2}}$

Tangentielle polygoner

En tangential polygon er en polygon hver af hvis sider er tangent til en bestemt cirkel, kaldes dens incircle . Hver trekant er en tangential polygon, ligesom enhver almindelig polygon af et vilkårligt antal sider; derudover er der for hvert antal polygonsider et uendeligt antal ikke- kongruente tangentielle polygoner.

Tangent firkantssætning og indskrevne cirkler

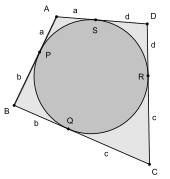
En tangential firsidede ABCD er en lukket figur med fire lige sider, som tangerer en given cirkel C . Tilsvarende, cirklen C er indskrevet i den firkant ABCD. Ved Pitot -sætningen er summen af ​​modsatte sider af en sådan firkant ens, dvs.

${\ displaystyle {\ overline {AB}}+{\ overline {CD}} = {\ overline {BC}}+{\ overline {DA}}.}$

Tangential firkant

Denne konklusion følger af lighed mellem tangentsegmenterne fra firkantens fire hjørner. Lad tangentpunkterne betegnes som P (på segment AB), Q (på segment BC), R (på segment CD) og S (på segment DA). De symmetriske tangentsegmenter omkring hvert punkt i ABCD er ens, fx BP = BQ = b , CQ = CR = c , DR = DS = d og AS = AP = a . Men hver side af firkanten er sammensat af to sådanne tangentsegmenter

${\ displaystyle {\ overline {AB}}+{\ overline {CD}} = (a+b)+(c+d) = {\ overline {BC}}+{\ overline {DA}} = (b+ c)+(d+a)}$

beviser sætningen.

Det omvendte er også sandt: en cirkel kan indskrives i hver firkant, hvor længderne på modsatte sider summerer til den samme værdi.

Denne sætning og dens omvendte har forskellige anvendelser. For eksempel viser de straks, at intet rektangel kan have en indskrevet cirkel, medmindre det er en firkant , og at hver rhombus har en indskrevet cirkel, hvorimod et generelt parallelogram ikke gør det.

Tangentlinjer til to cirkler

Det ydre (ovenfor) og indre (under) homothetiske center S for de to cirkler.

For to cirkler er der generelt fire forskellige linjer, der tangerer begge ( bitangent ) - hvis de to cirkler er uden for hinanden - men i degenererede tilfælde kan der være et vilkårligt tal mellem nul og fire bitangentlinjer; disse behandles nedenfor. For to af disse, de ydre tangentlinjer, falder cirklerne på samme side af linjen; for de to andre, de indre tangentlinjer, falder cirklerne på modsatte sider af linjen. De ydre tangentlinjer skærer hinanden i det ydre homotetiske center , hvorimod de indre tangentlinjer skærer hinanden i det interne homotetiske center. Både de eksterne og indre homotetiske centre ligger på linjen af ​​centre (linjen, der forbinder midten af ​​de to cirkler), tættere på midten af ​​den mindre cirkel: det indre center er i segmentet mellem de to cirkler, mens det ydre center er ikke mellem punkterne, men derimod udenfor, på siden af ​​midten af ​​den mindre cirkel. Hvis de to cirkler har samme radius, er der stadig fire bitangenter, men de ydre tangentlinjer er parallelle, og der er ikke noget eksternt center i affinplanet ; i det projektive plan ligger det ydre homothetiske centrum på det sted i det uendelige svarende til hældningen af ​​disse linjer.

Ydre tangent

Finde ydre tangent. To cirkels ydre tangenter.

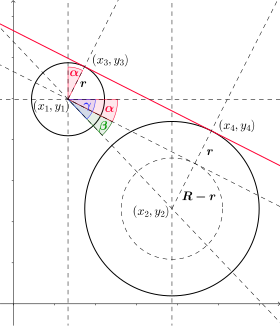
Den røde linje forbinder punkterne og er den ydre tangent mellem de to cirkler. Givne punkter , punkterne , kan let beregnes ved hjælp af vinklen : ${\ displaystyle (x_ {3}, y_ {3})}}$${\ displaystyle (x_ {4}, y_ {4})}$${\ displaystyle (x_ {1}, y_ {1})}$${\ displaystyle (x_ {2}, y_ {2})}$${\ displaystyle (x_ {3}, y_ {3})}}$${\ displaystyle (x_ {4}, y_ {4})}$${\ displaystyle \ alpha}$

${\ displaystyle {\ begin {align} x_ {3} & = x_ {1} \ pm r \ sin \ alpha \\ y_ {3} & = y_ {1} \ pm r \ cos \ alpha \\ x_ {4 } & = x_ {2} \ pm R \ sin \ alpha \\ y_ {4} & = y_ {2} \ pm R \ cos \ alpha \\\ end {align}}}$

Her noterer R og r radierne for de to cirkler, og vinklen kan beregnes ved hjælp af grundlæggende trigonometri. Du har med og . ${\ displaystyle \ alpha}$${\ displaystyle \ alpha = \ gamma -\ beta}$${\ displaystyle \ gamma =-\ arctan \ venstre ({\ tfrac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}} \ højre)}$${\ displaystyle \ beta = \ pm \ arcsin \ left ({\ tfrac {Rr} {\ sqrt {(x_ {2} -x_ {1})^{2}+(y_ {2} -y_ {1}) ^{2}}}} \ højre)}$

Indre tangent

Indre tangent. De ydre tangentlinjer passerer gennem det indre homotiske center.

En indre tangent er en tangent, der skærer segmentet, der forbinder to cirkels centre. Bemærk, at den indre tangent ikke vil blive defineret i tilfælde, hvor de to cirkler overlapper hinanden.

Konstruktion

Bitangentlinjerne kan konstrueres enten ved at konstruere de homothetiske centre, som beskrevet i denne artikel, og derefter konstruere tangentlinjerne gennem det homothetic center, der er tangent til en cirkel, ved en af ​​metoderne beskrevet ovenfor. Den resulterende linje vil derefter også være tangent til den anden cirkel. Alternativt kan tangentlinjerne og tangentpunkterne konstrueres mere direkte som beskrevet nedenfor. Bemærk, at i konstruerede tilfælde nedbrydes disse konstruktioner; for at forenkle eksponeringen diskuteres dette ikke i dette afsnit, men en form for konstruktionen kan fungere i grænsetilfælde (f.eks. to cirkler, der tangerer på et tidspunkt).

Syntetisk geometri

Lad O ₁ og O ₂ være centrum for de to cirkler, C ₁ og C ₂ og lad r ₁ og r ₂ være deres radier , med r ₁  >  r ₂ ; med andre ord er cirkel C ₁ defineret som den største af de to cirkler. To forskellige metoder kan bruges til at konstruere de eksterne og interne tangentlinjer.

Eksterne tangenter

Konstruktion af den ydre tangent

En ny cirkel C ₃ med radius r ₁  -  r ₂ tegnes centreret om O ₁ . Ved hjælp af metoden ovenfor trækkes to linjer fra O ₂ , der tangerer denne nye cirkel. Disse linjer er parallelle med de ønskede tangent linjer, fordi situationen svarer til krympning begge cirkler C ₁ og C ₂ af en konstant mængde, r ₂ , der krymper C ₂ til et punkt. To radiale linier kan drages fra centrum O ₁ gennem tangentpunkterne på C ₃ ; disse intersect C ₁ ved de ønskede tangentpunkterne. De ønskede eksterne tangentlinjer er linjerne vinkelret på disse radiale linjer ved disse tangentpunkter, som kan konstrueres som beskrevet ovenfor.

Indre tangenter

Konstruktion af den indre tangent

En ny cirkel C ₃ med radius r ₁  +  r ₂ tegnes centreret om O ₁ . Ved hjælp af metoden ovenfor trækkes to linjer fra O ₂ , der tangerer denne nye cirkel. Disse linjer er parallelle med de ønskede tangent linjer, fordi situationen svarer til krympning C ₂ til et punkt, mens ekspanderende C ₁ ved en konstant mængde, r ₂ . To radiale linier kan drages fra centrum O ₁ gennem tangentpunkterne på C ₃ ; disse intersect C ₁ ved de ønskede tangentpunkterne. De ønskede indre tangentlinjer er linjerne vinkelret på disse radiale linjer ved disse tangentpunkter, som kan konstrueres som beskrevet ovenfor.

Analytisk geometri

Lad cirklerne have centre c ₁ = ( x ₁ , y ₁ ) og c ₂ = ( x ₂ , y ₂ ) med radius henholdsvis r ₁ og r ₂ . Ved at udtrykke en linje ved ligningen med normaliseringen a ²  +  b ²  = 1, opfylder en bitangent linje: ${\ displaystyle ax+by+c = 0,}$

aks ₁  +  med ₁  +  c  =  r ₁ og

ax ₂  +  ved ₂  +  c  =  r ₂ .

Løsning for ved at trække det første fra det andet udbytte ${\ displaystyle (a, b, c)}$

en Δ x  +  b Δ y  = Δ r

hvor Δ x  =  x ₂  -  x ₁ , Δ y  =  y ₂  -  y ₁ og Δ r  =  r ₂  -  r ₁ .

Hvis afstanden er fra c ₁ til c _2, kan vi normalisere med X  = Δ x / d , Y  = Δ y / d og R  = Δ r / d for at forenkle ligninger, hvilket giver ligningerne aX  +  bY  =  R og a ²  +  b ²  = 1, løse disse for at få to løsninger ( k  = ± 1) for de to eksterne tangentlinjer: ${\ displaystyle d = {\ sqrt {(\ Delta x)^{2}+(\ Delta y)^{2}}}}$

a  =  RX  -  kY √ (1 -  R ² )

b  =  RY  +  kX √ (1 -  R ² )

c  =  r ₁  - ( aks ₁  +  x ₁ )

Geometrisk svarer dette til at beregne den vinkel, der dannes af tangentlinjerne og linjen af ​​centre, og derefter bruge den til at rotere ligningen for centerlinjen for at give en ligning for tangentlinjen. Vinklen beregnes ved at beregne de trigonometriske funktioner i en højre trekant, hvis hjørner er (eksternt) homotetisk centrum, et centrum i en cirkel og et tangentpunkt; hypotenusen ligger på tangentlinjen, radius er modsat vinklen, og den tilstødende side ligger på linjen af ​​centre.

( X ,  Y ) er enhedsvektoren, der peger fra c ₁ til c ₂ , mens R er hvor er vinklen mellem centerlinjen og en tangentlinje. er derefter (afhængigt af tegnet på , tilsvarende rotationsretningen), og ovenstående ligninger er rotation af ( X ,  Y ) ved hjælp af rotationsmatricen: ${\ displaystyle \ cos \ theta}$${\ displaystyle \ theta}$${\ displaystyle \ sin \ theta}$${\ displaystyle \ pm {\ sqrt {1-R^{2}}}}$${\ displaystyle \ theta}$${\ displaystyle \ pm \ theta,}$

${\ displaystyle {\ begin {pmatrix} R & \ mp {\ sqrt {1-R^{2}}} \\\ pm {\ sqrt {1-R^{2}}} & R \ end {pmatrix}}}$

k  = 1 er tangentlinjen til højre for cirklerne fra c ₁ til c ₂ .

k  = −1 er tangentlinjen til højre for cirklerne fra c ₂ til c ₁ .

Ovenstående forudsætter, at hver cirkel har en positiv radius. Hvis r ₁ er positiv og r ₂ negativ, vil c ₁ ligge til venstre for hver linje og c ₂ til højre, og de to tangentlinjer krydser. På denne måde opnås alle fire løsninger. Skiftetegn for begge radiusafbrydere k  = 1 og k  = −1.

Vektorer

Finde ydre tangent. Cirkel tangenter.

Generelt er tangenspunkterne t ₁ og t ₂ for de fire linjer, der tangerer to cirkler med centre v ₁ og v ₂ og radius r ₁ og r ₂ , givet ved at løse de samtidige ligninger:

${\ displaystyle {\ begin {align} (t_ {2} -v_ {2}) \ cdot (t_ {2} -t_ {1}) & = 0 \\ (t_ {1} -v_ {1}) \ cdot (t_ {2} -t_ {1}) & = 0 \\ (t_ {1} -v_ {1}) \ cdot (t_ {1} -v_ {1}) & = r_ {1}^{2 } \\ (t_ {2} -v_ {2}) \ cdot (t_ {2} -v_ {2}) & = r_ {2}^{2} \\\ end {align}}}$

Disse ligninger udtrykker, at tangentlinjen, som er parallel med, er vinkelret på radierne, og at tangentpunkterne ligger på deres respektive cirkler. ${\ displaystyle t_ {2} -t_ {1},}$

Disse er fire kvadratiske ligninger i to todimensionelle vektorvariabler, og generelt vil position have fire par løsninger.

Degenererede tilfælde

To forskellige cirkler kan have mellem nul og fire bitangentlinjer afhængigt af konfiguration; disse kan klassificeres med hensyn til afstanden mellem centrene og radierne. Hvis det tælles med multiplicitet (tæller en fælles tangens to gange) er der nul, to eller fire bitangentlinjer. Bitangentlinjer kan også generaliseres til cirkler med negativ eller nul radius. De degenererede sager og mangfoldighederne kan også forstås i form af grænser for andre konfigurationer - f.eks. En grænse på to cirkler, der næsten rører, og bevæger en, så de rører, eller en cirkel med lille radius, der krymper til en cirkel med nul radius .

• Hvis cirklerne er uden for hinanden ( ), hvilket er en generel position , er der fire bitangenter.${\ displaystyle d> r_ {1}+r_ {2}}$
• Hvis de rører eksternt på et tidspunkt ( ) - har et punkt med ekstern tangens - så har de to eksterne bitangenter og en intern bitangent, nemlig den fælles tangentlinje. Denne fælles tangentlinje har mangfoldighed to, da den adskiller cirklerne (en til venstre, en til højre) for enten retning (retning).${\ displaystyle d = r_ {1}+r_ {2}}$
• Hvis cirklerne skærer hinanden i to punkter ( ), så har de ingen interne bitangenter og to eksterne bitangenter (de kan ikke adskilles, fordi de skærer hinanden, derfor ingen interne bitangenter).${\ displaystyle | r_ {1} -r_ {2} | <d <r_ {1}+r_ {2}}$
• Hvis cirklerne berører internt på et tidspunkt ( ) - har et punkt med intern tangens - så har de ingen interne bitangenter og en ekstern bitangent, nemlig den fælles tangentlinje, som har multiplicitet to, som ovenfor.${\ displaystyle d = | r_ {1} -r_ {2} |}$
• Hvis en cirkel er helt inde i den anden ( ), så har de ingen bitangenter, da en tangentlinje til den ydre cirkel ikke skærer den indre cirkel, eller omvendt er en tangentlinje til den indre cirkel en sekant linje til den ydre cirkel.${\ displaystyle d <| r_ {1} -r_ {2} |}$

Endelig, hvis de to cirkler er identiske, er enhver tangent til cirklen en fælles tangent og dermed (ekstern) bitangent, så der er en cirkels værdi af bitangenter.

Ydermere kan begrebet bitangentlinjer udvides til cirkler med negativ radius (det samme punktpunkt, men betragtes som "indefra"), i hvilket tilfælde radierne har modsat tegn (den ene cirkel har en negativ radius, og den anden har positiv radius) de eksterne og interne homotetiske centre og eksterne og interne bitangenter skiftes, mens hvis radierne har det samme tegn (både positive radier eller begge negative radier) har "eksterne" og "interne" samme sædvanlige forstand (skift af et tegn skifter dem, så skifte begge skifter dem tilbage). ${\ displaystyle x^{2}+y^{2} = (-r)^{2},}$

Bitangentlinjer kan også defineres, når en eller begge cirkler har radius nul. I dette tilfælde er cirklen med radius nul et dobbeltpunkt, og derfor skærer enhver linje, der passerer det, punktet med multiplicitet to, og er derfor "tangent". Hvis en cirkel har radius nul, er en bitangentlinje simpelthen en linje, der tangerer cirklen og passerer gennem punktet, og tælles med multiplicitet to. Hvis begge cirkler har radius nul, er bitangentlinjen den linje, de definerer, og tælles med multiplicitet fire.

Bemærk, at i disse degenererede tilfælde eksisterer det ydre og indre homothetiske center generelt stadig (det ydre centrum er uendeligt, hvis radierne er ens), undtagen hvis cirklerne falder sammen, i hvilket tilfælde det eksterne center ikke er defineret, eller hvis begge cirkler er har radius nul, i hvilket tilfælde det interne center ikke er defineret.

Ansøgninger

Bælte problem

De indre og ydre tangentlinjer er nyttige til at løse bælteproblemet , som er at beregne længden af ​​et bælte eller reb, der er nødvendigt for at passe tæt over to remskiver. Hvis båndet anses for at være en matematisk linje med ubetydelig tykkelse, og hvis det antages, at begge remskiver ligger i nøjagtig det samme plan, går problemet ud på at summere længderne af de relevante tangenslinjesegmenter med længderne af cirkelbuer, der er underlagt af bælte. Hvis bæltet vikles om hjulene for at krydse, er de indre tangenslinjesegmenter relevante. Omvendt, hvis bæltet vikles udvendigt omkring remskiverne, er de udvendige tangentlinjesegmenter relevante; denne sag kaldes undertiden remskive -problemet .

Tangentlinjer til tre cirkler: Monges sætning

For tre cirkler betegnet med C ₁ , C ₂ og C ₃ er der tre par cirkler ( C ₁ C ₂ , C ₂ C ₃ og C ₁ C ₃ ). Da hvert cirkelpar har to homotetiske centre, er der i alt seks homotetiske centre . Gaspard Monge viste i begyndelsen af ​​1800 -tallet, at disse seks punkter ligger på fire linjer, hver linje har tre kollinære punkter.

Problem med Apollonius

Animation, der viser den inversive transformation af et Apollonius -problem. De blå og røde cirkler svulmer til tangens og er omvendt i den grå cirkel og producerer to lige linjer. De gule løsninger findes ved at skubbe en cirkel mellem dem, indtil den rører den transformerede grønne cirkel indefra eller udenfra.

Mange særlige tilfælde af Apollonius 'problem indebærer at finde en cirkel, der tangerer en eller flere linjer. Den enkleste af disse er at konstruere cirkler, der tangerer tre givne linjer ( LLL -problemet). For at løse dette problem skal midten af ​​en sådan cirkel ligge på en vinkelhalveringslinje af ethvert par af linjerne; der er to vinkelforskærende linjer for hvert skæringspunkt mellem to linjer. Skæringspunkterne mellem disse vinkelhalveringslinjer giver centre for opløsningscirkler. Der er generelt fire sådanne cirkler, den indskrevne cirkel i trekanten dannet ved skæringen mellem de tre linjer og de tre afskrevne cirkler.

Et generelt Apollonius -problem kan omdannes til det enklere problem med cirkel, der tangerer en cirkel og to parallelle linjer (i sig selv et specielt tilfælde af LLC -specialtilfældet). For at opnå dette er det tilstrækkeligt at skalere to af de tre givne cirkler, indtil de bare rører, dvs. er tangenter. En inversion i deres tangentpunkt med hensyn til en cirkel med passende radius forvandler de to rørende givne cirkler til to parallelle linjer og den tredje givne cirkel til en anden cirkel. Således kan løsningerne findes ved at glide en cirkel med konstant radius mellem to parallelle linjer, indtil den kommer i kontakt med den transformerede tredje cirkel. Re-inversion producerer de tilsvarende løsninger på det oprindelige problem.

Generaliseringer

Begrebet en tangentlinje og tangentpunkt kan generaliseres til et polpunkt Q og dets tilsvarende polære linje q . Punkterne P og Q er inverser af hinanden i forhold til cirklen.

Begrebet en tangentlinje til en eller flere cirkler kan generaliseres på flere måder. For det første kan det konjugerede forhold mellem tangentpunkter og tangentlinjer generaliseres til polpunkter og polære linjer , hvor polpunkterne kan være hvor som helst, ikke kun på cirkelens omkreds. For det andet er foreningen af ​​to cirkler et særligt ( reducerbart ) tilfælde af en kvartsplankurve , og de ydre og indre tangentlinjer er bitangenter til denne kvartalkurve . En generisk kvartalkurve har 28 bitangenter.

En tredje generalisering betragter tangentcirkler frem for tangentlinjer; en tangentlinje kan betragtes som en tangentcirkel med uendelig radius. Især er de eksterne tangentlinjer til to cirkler begrænsende tilfælde af en familie af cirkler, der internt eller eksternt tangenterer til begge cirkler, mens de interne tangentlinjer er begrænsende tilfælde af en familie af cirkler, der internt tangenterer til en og eksternt tangenterer til den anden af ​​de to cirkler.

I Möbius eller inversiv geometri ses linjer som cirkler gennem et punkt "i det uendelige", og for enhver linje og enhver cirkel er der en Möbius -transformation, der kortlægger den ene til den anden. I Möbius -geometri bliver tangens mellem en linje og en cirkel et specielt tilfælde af tangens mellem to cirkler. Denne ækvivalens udvides yderligere i Lie sfære geometri .

Radius og tangentlinje er vinkelret på et punkt i en cirkel og hyperbolsk-ortogonal ved et punkt i enhedens hyperbola . Den parametriske repræsentation af enheden hyperbel via radius vektor er den derivat af p ( a ) peger i retning af tangenten ved p ( a ), og er den radius og tangenten er hyperbolske ortogonale på en da er reflektioner af hinanden i asymptote y = x af enhedens hyperbola. Når de tolkes som split-komplekse tal (hvor jj = +1), tilfredsstiller de to tal${\ displaystyle p (a) \ = \ (\ cosh a, \ sinh a).}$${\ displaystyle {\ frac {dp} {da}} \ = \ (\ sinh a, \ cosh a).}$${\ displaystyle p (a) \ {\ tekst {og}} \ {\ frac {dp} {da}}}$${\ displaystyle jp (a) \ = \ {\ frac {dp} {da}}.}$

Referencer

eksterne links

• Weisstein, Eric W. "Tangentlinjer til en cirkel" . MathWorld .
• Weisstein, Eric W. "Tangentlinjer til to cirkler" . MathWorld .