Tangentrum - Tangent space

I matematik , den tangentrummet af en manifold generaliseres til højere dimensioner begrebet tangentplaner til overflader i tre dimensioner og tangenten linjer til kurver i to dimensioner. I fysikkonteksten kan tangensrummet til en manifold på et punkt ses som rummet med mulige hastigheder for en partikel, der bevæger sig på manifolden.

Uformel beskrivelse

En billedlig repræsentation af tangentrummet i et enkelt punkt på en kugle . En vektor i dette tangentrum repræsenterer en mulig hastighed ved . Efter at have bevæget sig i den retning til et nærliggende punkt, ville hastigheden derefter blive givet af en vektor i tangentrummet på dette punkt - et andet tangentrum, der ikke vises.${\ displaystyle x}$${\ displaystyle x}$

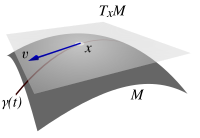
I differentialgeometri kan man ved hvert punkt i en differentierbar manifold knytte et tangensrum - et reelt vektorrum, der intuitivt indeholder de mulige retninger, som man tangentielt kan passere igennem . Elementerne i tangensrummet ved kaldes tangentvektorerne kl . Dette er en generalisering af forestillingen om en vektor , baseret på et givet startpunkt, i et euklidisk rum . Den dimension af tangenten plads på hvert punkt af en tilsluttet manifold er den samme som for den manifold selv. ${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$

For eksempel, hvis den givne manifold er en - kugle , så kan man forestille sig tangensrummet på et punkt som det plan, der berører kuglen på det punkt og er vinkelret på kuglens radius gennem punktet. Mere generelt, hvis en given manifold betragtes som en indlejret submanifold af euklidisk rum , så kan man forestille sig et tangentrum på denne bogstavelige måde. Dette var den traditionelle tilgang til at definere paralleltransport . Mange forfattere inden for differential geometri og generel relativitet anvender den. Mere strengt definerer dette et affint tangentrum, som adskiller sig fra rummet for tangentvektorer beskrevet af moderne terminologi. ${\ displaystyle 2}$

I algebraisk geometri er der derimod en iboende definition af tangensrummet på et punkt i en algebraisk variant, der giver et vektorrum med dimension i det mindste det af sig selv. De punkter, hvor tangensrummets dimension er præcis den , kaldes ikke-entalpunkter ; de andre kaldes entalpunkter . For eksempel har en kurve, der krydser sig selv, ikke en unik tangentlinje på det tidspunkt. De entydige punkter er dem, hvor "testen for at være en mangfoldighed" mislykkes. Se Zariski tangensrum . ${\ displaystyle V}$${\ displaystyle V}$${\ displaystyle p}$${\ displaystyle V}$${\ displaystyle V}$

Når tangentrummene i en manifold er blevet introduceret, kan man definere vektorfelter , som er abstraktioner af hastighedsfeltet for partikler, der bevæger sig i rummet. Et vektorfelt knytter en vektor fra tangentrummet på dette punkt til hvert punkt i manifolden på en jævn måde. Et sådant vektorfelt tjener til at definere en generaliseret almindelig differentialligning på en manifold: En løsning på en sådan differentialligning er en differentierbar kurve på manifolden, hvis derivat på et hvilket som helst tidspunkt er lig med tangensvektoren, der er knyttet til dette punkt med vektorfeltet.

Alle tangentrum i en manifold kan "limes sammen" for at danne en ny differentierbar manifold med dobbelt så stor størrelse som den originale manifold, kaldet manifoldens tangentbundt .

Formelle definitioner

Den uformelle beskrivelse ovenfor er afhængig af en manifolds evne til at blive indlejret i et omgivende vektorrum, så tangentvektorerne kan "stikke ud" af manifolden i det omgivende rum. Det er imidlertid mere bekvemt at definere forestillingen om et tangentrum, der udelukkende er baseret på selve manifolden. ${\ displaystyle \ mathbb {R} ^{m}}$

Der er forskellige ækvivalente måder at definere tangentrum på en manifold. Selvom definitionen via kurvenes hastighed intuitivt er den enkleste, er den også den mest besværlige at arbejde med. Mere elegante og abstrakte tilgange er beskrevet nedenfor.

Definition via tangentkurver

I det indlejrede-mangfoldige billede betragtes en tangentvektor på et punkt som hastigheden af en kurve, der passerer gennem punktet . Vi kan derfor definere en tangentvektor som en ækvivalensklasse af kurver, der passerer igennem, mens de tangerer hinanden ved . ${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$

Antag, at det er en differentierbar manifold (med glathed ) og det . Vælg et koordinatdiagram , hvor der er et åbent undersæt af indeholdende . Antag yderligere, at to kurver med er givet sådan, at begge er differentierbare i almindelig forstand (vi kalder disse differentierbare kurver initialiseret ved ). Derefter og siges at være ækvivalente ved hvis og kun hvis derivaterne af og ved er sammenfaldende. Dette definerer et ækvivalensforhold på sættet af alle differentierbare kurver initialiseret ved , og ækvivalensklasser for sådanne kurver er kendt som tangentvektorer af at . Ækvivalensklassen for en sådan kurve er betegnet med . Den tangentrummet af på , betegnet med , defineres derefter som mængden af alle tangentvektorer på ; det afhænger ikke af valget af koordinatdiagram . ${\ displaystyle M}$${\ displaystyle C^{k}}$ ${\ displaystyle k \ geq 1}$${\ displaystyle x \ i M}$ ${\ displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$${\ displaystyle U}$${\ displaystyle M}$${\ displaystyle x}$${\ displaystyle \ gamma _ {1}, \ gamma _ {2}: (-1,1) \ til M}$${\ displaystyle {\ gamma _ {1}} (0) = x = {\ gamma _ {2}} (0)}$${\ displaystyle \ varphi \ circ \ gamma _ {1}, \ varphi \ circ \ gamma _ {2}: (-1,1) \ to \ mathbb {R} ^{n}}$${\ displaystyle x}$${\ displaystyle \ gamma _ {1}}$${\ displaystyle \ gamma _ {2}}$${\ displaystyle 0}$${\ displaystyle \ varphi \ circ \ gamma _ {1}}$${\ displaystyle \ varphi \ circ \ gamma _ {2}}$${\ displaystyle 0}$${\ displaystyle x}$${\ displaystyle M}$${\ displaystyle x}$${\ displaystyle \ gamma}$${\ displaystyle \ gamma '(0)}$${\ displaystyle M}$${\ displaystyle x}$${\ displaystyle T_ {x} M}$${\ displaystyle x}$${\ displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$

Tangensrummet og en tangentvektor langs en kurve, der bevæger sig igennem .${\ displaystyle T_ {x} M}$${\ displaystyle v \ i T_ {x} M}$${\ displaystyle x \ i M}$

For at definere vektorrumsoperationer på bruger vi et diagram og definerer et kort efter hvor . Igen skal man kontrollere, at denne konstruktion ikke afhænger af det særlige diagram og den kurve, der bruges, og det gør det faktisk ikke. ${\ displaystyle T_ {x} M}$${\ displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$ ${\ displaystyle \ mathrm {d} {\ varphi} _ {x}: T_ {x} M \ til \ mathbb {R} ^{n}}$${\ displaystyle {\ mathrm {d} {\ varphi} _ {x}} (\ gamma '(0)) \ mathrel {\ stackrel {\ text {df}} {=}} \ venstre. {\ frac {\ mathrm {d}} {\ mathrm {d} {t}}} [(\ varphi \ circ \ gamma) (t)] \ right | _ {t = 0},}$${\ displaystyle \ gamma \ in \ gamma '(0)}$${\ displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$${\ displaystyle \ gamma}$

Kortet viser sig at være bijektiv og kan bruges til at overføre vektorrumsoperationer til og dermed gøre det sidste sæt til et -dimensionelt reelt vektorrum. ${\ displaystyle \ mathrm {d} {\ varphi} _ {x}}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle T_ {x} M}$${\ displaystyle n}$

Definition via afledninger

Antag nu, at det er en mangfoldighed. En reel funktion siges at tilhøre hvis og kun hvis der for hver koordinat diagram , kortet er uendeligt differentiabel. Bemærk, at det er en reel associativ algebra med hensyn til det punktvise produkt og summen af ​​funktioner og skalarmultiplikation. ${\ displaystyle M}$${\ displaystyle C^{\ infty}}$${\ displaystyle f: M \ til \ mathbb {R}}$${\ displaystyle {C^{\ infty}} (M)}$${\ displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$${\ displaystyle f \ circ \ varphi ^{-1}: \ varphi [U] \ subseteq \ mathbb {R} ^{n} \ to \ mathbb {R}}$${\ displaystyle {C^{\ infty}} (M)}$

Vælg et punkt . En afledning på er defineret som et lineært kort, der opfylder Leibniz -identiteten ${\ displaystyle x \ i M}$${\ displaystyle x}$ ${\ displaystyle D: {C^{\ infty}} (M) \ til \ mathbb {R}}$

${\ displaystyle \ forall f, g \ in {C^{\ infty}} (M): \ qquad D (fg) = D (f) \ cdot g (x)+f (x) \ cdot D (g) ,}$

som er modelleret efter produktreglen for beregning.

(For hver identisk konstante funktion følger det ). ${\ displaystyle f = {\ tekst {const}},}$${\ displaystyle D (f) = 0}$

Hvis vi definerer addition og skalarmultiplikation på sæt afledninger ved ${\ displaystyle x}$

• ${\ displaystyle (D_ {1}+D_ {2}) (f) \ mathrel {\ stackrel {\ text {df}} {=}} {D} _ {1} (f)+{D} _ {2 } (f)}$ og
• ${\ displaystyle (\ lambda \ cdot D) (f) \ mathrel {\ stackrel {\ text {df}} {=}} \ lambda \ cdot D (f)}$,

derefter få vi en reel vektorrum, som vi definerer som tangentrummet af på . ${\ displaystyle T_ {x} M}$${\ displaystyle M}$${\ displaystyle x}$

Generaliseringer

Generaliseringer af denne definition er f.eks. Mulige for komplekse manifolder og algebraiske sorter . Men i stedet for at undersøge afledninger, fra den fulde algebra funktioner, må man i stedet arbejde på niveau med bakterier af funktioner. Grunden til dette er, at strukturskiven måske ikke er fine til sådanne strukturer. Lad os f.eks. Være en algebraisk variant med strukturskår . Så Zariski tangent plads på et punkt er en samling af alle -derivations , hvor er jorden feltet og er stilken af på . ${\ displaystyle D}$${\ displaystyle X}$ ${\ displaystyle {\ mathcal {O}} _ {X}}$${\ displaystyle p \ i X}$${\ displaystyle \ mathbb {k}}$${\ displaystyle D: {\ mathcal {O}} _ {X, p} \ to \ mathbb {k}}$${\ displaystyle \ mathbb {k}}$${\ displaystyle {\ mathcal {O}} _ {X, s}}$${\ displaystyle {\ mathcal {O}} _ {X}}$${\ displaystyle p}$

Definitionernes ækvivalens

For og en differentierbar kurve , der definerer (hvor derivatet tages i almindelig forstand, fordi det er en funktion fra til ). Man kan konstatere, at det er en afledning ved punktet, og at ækvivalente kurver giver den samme afledning. Således kan vi for en ækvivalensklasse definere, hvor kurven er valgt vilkårligt. Kortet er en vektorrumsomorfisme mellem rummet i ækvivalensklasserne og afledningenes ved punktet${\ displaystyle x \ i M}$${\ displaystyle \ gamma: (-1,1) \ til M}$${\ displaystyle \ gamma (0) = x,}$${\ displaystyle {D _ {\ gamma}} (f) \ mathrel {\ stackrel {\ text {df}} {=}} (f \ circ \ gamma) '(0)}$${\ displaystyle f \ circ \ gamma}$${\ displaystyle (-1,1)}$${\ displaystyle \ mathbb {R}}$${\ displaystyle D _ {\ gamma} (f)}$${\ displaystyle x,}$${\ displaystyle \ gamma '(0),}$${\ displaystyle {D _ {\ gamma '(0)}} (f) \ mathrel {\ stackrel {\ text {df}} {=}} (f \ circ \ gamma)' (0),}$${\ displaystyle \ gamma \ in \ gamma '(0)}$${\ displaystyle \ gamma '(0) \ mapsto D _ {\ gamma' (0)}}$${\ displaystyle \ gamma '(0)}$${\ displaystyle x.}$

Definition via cotangent -mellemrum

Igen starter vi med en mangfoldighed og et punkt . Overvej ideal af det består af alle glatte funktioner forsvindende på , det vil sige, . Så og er begge virkelige vektorrum, og kvotrummet kan påvises at være isomorft for cotangentrummet ved brug af Taylors sætning . Tangentrummet kan derefter defineres som det dobbelte rum af . ${\ displaystyle C^{\ infty}}$${\ displaystyle M}$${\ displaystyle x \ i M}$ ${\ displaystyle I}$${\ displaystyle C^{\ infty} (M)}$${\ displaystyle f}$${\ displaystyle x}$${\ displaystyle f (x) = 0}$${\ displaystyle I}$${\ displaystyle I^{2}}$ ${\ displaystyle I/I^{2}}$ ${\ displaystyle T_ {x}^{*} M}$${\ displaystyle T_ {x} M}$${\ displaystyle I/I^{2}}$

Selvom denne definition er den mest abstrakte, er den også den, der lettest kan overføres til andre indstillinger, for eksempel til de sorter, der betragtes i algebraisk geometri .

Hvis er en afledning ved , så for hver , hvilket betyder, at det giver anledning til et lineært kort . Omvendt, hvis er et lineært kort, så definerer en afledning ved . Dette giver en ækvivalens mellem tangentrum defineret via afledninger og tangentrum defineret via cotangentrum. ${\ displaystyle D}$${\ displaystyle x}$${\ displaystyle D (f) = 0}$${\ displaystyle f \ i I^{2}}$${\ displaystyle D}$${\ displaystyle I/I^{2} \ to \ mathbb {R}}$${\ displaystyle r: I/I^{2} \ til \ mathbb {R}}$${\ displaystyle D (f) \ mathrel {\ stackrel {\ text {def}} {=}} r \ venstre ((ff (x))+I^{2} \ right)}$${\ displaystyle x}$

Ejendomme

Hvis er en åben delmængde af , så er en mangfoldighed på en naturlig måde (tag koordinatdiagrammer for at være identitetskort på åbne undersæt af ), og tangentrummene er alle naturligt identificeret med . ${\ displaystyle M}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle M}$${\ displaystyle C^{\ infty}}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle \ mathbb {R} ^{n}}$

Tangentvektorer som retningsafledte derivater

En anden måde at tænke på tangentvektorer er som retningsafledte derivater . Givet en vektor i , definerer man det tilsvarende retningsderivat på et punkt ved ${\ displaystyle v}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle x \ in \ mathbb {R} ^{n}}$

${\ displaystyle \ forall f \ in {C ^{\ infty}} (\ mathbb {R} ^{n}): \ qquad (D_ {v} f) (x) \ mathrel {\ stackrel {\ text {df }} {=}} \ venstre. {\ frac {\ mathrm {d}} {\ mathrm {d} {t}}} [f (x+tv)] \ højre | _ {t = 0} = \ sum _ {i = 1}^{n} v^{i} {\ frac {\ delvis f} {\ delvis x^{i}}} (x).}$

Dette kort er naturligvis en afledning ved . Desuden er hver afledning på et tidspunkt i denne form. Derfor er der en en-til-en-korrespondance mellem vektorer (tænkt som tangentvektorer på et punkt) og afledninger på et punkt. ${\ displaystyle x}$${\ displaystyle \ mathbb {R} ^{n}}$

Da tangentvektorer til en generel manifold på et punkt kan defineres som afledninger på det tidspunkt, er det naturligt at tænke på dem som retningsbestemte derivater. Specifikt, hvis er en tangentvektor til på et punkt (tænkt som en afledning), skal du definere retningsderivatet i retningen ved at ${\ displaystyle v}$${\ displaystyle M}$${\ displaystyle x}$${\ displaystyle D_ {v}}$${\ displaystyle v}$

${\ displaystyle \ forall f \ in {C^{\ infty}} (M): \ qquad {D_ {v}} (f) \ mathrel {\ stackrel {\ text {df}} {=}} v (f ).}$

Hvis vi tænker på som den indledende hastighed for en differentierbar kurve initialiseret til , dvs. i stedet defineres ved ${\ displaystyle v}$${\ displaystyle \ gamma}$${\ displaystyle x}$${\ displaystyle v = \ gamma '(0)}$${\ displaystyle D_ {v}}$

${\ displaystyle \ forall f \ in {C^{\ infty}} (M): \ qquad {D_ {v}} (f) \ mathrel {\ stackrel {\ text {df}} {=}} (f \ circ \ gamma) '(0).}$

Grundlaget for tangensrummet på et punkt

For en manifold , hvis et diagram er givet med , så kan man definere et ordnet grundlag for by ${\ displaystyle C^{\ infty}}$${\ displaystyle M}$${\ displaystyle \ varphi = (x^{1}, \ ldots, x^{n}): U \ til \ mathbb {R}^{n}}$${\ displaystyle p \ i U}$${\ displaystyle \ left \ {\ left ({\ frac {\ partial} {\ partial x^{1}}} \ right) _ {p}, \ dots, \ left ({\ frac {\ partial} {\ delvis x^{n}}} \ højre) _ {p} \ højre \}}$${\ displaystyle T_ {p} M}$

${\ displaystyle \ forall i \ in \ {1, \ ldots, n \}, ~ \ forall f \ in {C^{\ infty}} (M): \ qquad {\ left ({\ frac {\ partial} {\ delvis x^{i}}} \ højre) _ {p}} (f) \ mathrel {\ stackrel {\ text {df}} {=}} \ venstre ({\ frac {\ partiel} {\ delvis x ^{i}}} {\ Big (} f \ circ \ varphi ^{-1} {\ Big)} \ right) {\ Big (} \ varphi (p) {\ Big)}.}$

Så for hver tangentvektor har man ${\ displaystyle v \ i T_ {p} M}$

${\ displaystyle v = \ sum _ {i = 1}^{n} v^{i} \ cdot \ venstre ({\ frac {\ partial} {\ delvis x^{i}}} \ højre) _ {p }.}$

Denne formel udtrykker derfor som en lineær kombination af basis -tangensvektorer defineret af koordinatdiagrammet . ${\ displaystyle v}$${\ displaystyle \ venstre ({\ frac {\ partial} {\ delvis x^{i}}} \ højre) _ {p} \ i T_ {p} M}$${\ displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$

Afledningen af ​​et kort

Hvert glat (eller differentierbart) kort mellem glatte (eller differentierbare) manifolder fremkalder naturlige lineære kort mellem deres tilsvarende tangentrum: ${\ displaystyle \ varphi: M \ til N}$

${\ displaystyle \ mathrm {d} {\ varphi} _ {x}: T_ {x} M \ til T _ {\ varphi (x)} N.}$

Hvis tangensrummet er defineret via differentierbare kurver, er dette kort defineret af

${\ displaystyle {\ mathrm {d} {\ varphi} _ {x}} (\ gamma '(0)) \ mathrel {\ stackrel {\ text {df}} {=}} (\ varphi \ circ \ gamma) '(0).}$

Hvis tangentrummet i stedet defineres via afledninger, er dette kort defineret af

${\ displaystyle [\ mathrm {d} {\ varphi} _ {x} (D)] (f) \ mathrel {\ stackrel {\ text {df}} {=}} D (f \ circ \ varphi).}$

Den lineære kort kaldes skiftevis den derivat , samlede derivat , differential , eller pushforward af på . Det udtrykkes ofte ved hjælp af en række andre notationer: ${\ displaystyle \ mathrm {d} {\ varphi} _ {x}}$${\ displaystyle \ varphi}$${\ displaystyle x}$

${\ displaystyle D \ varphi _ {x}, \ qquad (\ varphi _ {*}) _ {x}, \ qquad \ varphi '(x).}$

På en måde er derivatet den bedste lineære tilnærmelse til nær . Bemærk, at når , derefter kort falder sammen med den sædvanlige forestilling om forskellen af funktionen . I lokale koordinater er derivatet givet af jakobianeren . ${\ displaystyle \ varphi}$${\ displaystyle x}$${\ displaystyle N = \ mathbb {R}}$${\ displaystyle \ mathrm {d} {\ varphi} _ {x}: T_ {x} M \ til \ mathbb {R}}$${\ displaystyle \ varphi}$${\ displaystyle \ varphi}$

Et vigtigt resultat vedrørende det afledte kort er følgende:

Sætning . Hvis der er en lokal diffeomorfisme ved in , så er en lineær isomorfisme . Omvendt, hvis den er kontinuerligt differentierbar og er en isomorfisme, så er der et åbent kvarter af sådanne, der kort deffeomorfisk indgår i dets billede.${\ displaystyle \ varphi: M \ til N}$${\ displaystyle x}$${\ displaystyle M}$${\ displaystyle \ mathrm {d} {\ varphi} _ {x}: T_ {x} M \ til T _ {\ varphi (x)} N}$${\ displaystyle \ varphi: M \ til N}$${\ displaystyle \ mathrm {d} {\ varphi} _ {x}}$ ${\ displaystyle U}$${\ displaystyle x}$${\ displaystyle \ varphi}$${\ displaystyle U}$

Dette er en generalisering af den inverse funktions sætning til kort mellem manifolder.

Se også

• Koordinatinduceret grundlag
• Cotangent plads
• Differentialgeometri af kurver
• Eksponentielt kort
• Vector plads

Noter

Referencer

• Lee, Jeffrey M. (2009), Manifolds and Differential Geometry , Graduate Studies in Mathematics , 107 , Providence: American Mathematical Society.
• Michor, Peter W. (2008), Emner i differential geometri , kandidatstudier i matematik, 93 , Providence: American Mathematical Society.
• Spivak, Michael (1965), Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus , WA Benjamin, Inc., ISBN 978-0-8053-9021-6.

eksterne links

• Tangent Planes på MathWorld