Mercator projektion - Mercator projection

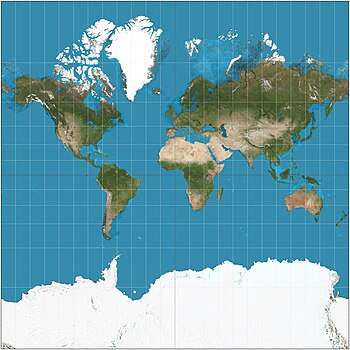
Den mercatorprojektion ( / m ər k eɪ t ər / ) er en cylindrisk kort fremspring præsenteret af flamske geograf og kartograf Gerardus Mercator i 1569. Det blev standard kort fremskrivning for navigation fordi det er enestående i repræsentere nord som op og syd som ned overalt og samtidig bevare lokale retninger og former. Kortet er derved konformt . Som en bivirkning puster Mercator -projektionen størrelsen af ​​objekter væk fra ækvator. Denne inflation er meget lille nær ækvator, men accelererer med stigende breddegrad for at blive uendelig ved polerne. Som et resultat heraf fremstår landmasser som Grønland og Antarktis langt større, end de rent faktisk er i forhold til landmasser nær ækvator, såsom Centralafrika.

Historie

Der er en del kontroverser om Mercators oprindelse. Tysk polyhistor Erhard Etzlaub indgraveret miniature "kompas maps" (ca. 10 x 8 cm) i Europa og dele af Afrika, der strakte breddegrader 0 ° -67 ° for at tillade justering af hans bærbare lommeformat solure . Projektionen fundet på disse kort, der stammer fra 1511, blev af Snyder i 1987 oplyst at være den samme projektion som Mercators. I betragtning af geometrien i et solur kan disse kort dog godt have været baseret på den lignende centrale cylindriske projektion , et begrænsende tilfælde af den gnomoniske projektion , som er grundlaget for et solur. Snyder ændrer sin vurdering til "en lignende fremskrivning" i 1994.

Joseph Needham , en historiker i Kina, skrev, at kineserne udviklede Mercator -projektionen hundredvis af år før Mercator gjorde det og brugte det på stjernekort under Song -dynastiet . Dette var imidlertid et enkelt og almindeligt tilfælde af fejlidentifikation. Projektionen i brug var den ækvektangangulære projektion .

Den portugisiske matematiker og kosmograf Pedro Nunes beskrev først det matematiske princip om loxodrome og dets anvendelse i marinefart. I 1537 foreslog han at konstruere et nautisk atlas sammensat af flere store ark i det cylindriske ækvidistante projektion som en måde at minimere forvrængning af retninger. Hvis disse ark blev bragt i samme skala og samlet, ville de tilnærme Mercator -projektionen.

I 1569 annoncerede Gerhard Kremer, kendt under sit handelsnavn Gerardus Mercator, en ny projektion ved at udgive et stort planiskfærisk kort, der måler 202 x 124 cm (trykt i atten separate ark). Mercator betegnede kortet Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendata : "En ny og udvidet beskrivelse af Jorden korrigeret for brug af sejlere". Denne titel sammen med en udførlig forklaring på, hvordan man bruger den projektion, der vises som et tekstafsnit på kortet, viser, at Mercator forstod præcis, hvad han havde opnået, og at han havde til hensigt at projicere det som hjælp til navigation. Mercator forklarede aldrig konstruktionsmetoden eller hvordan han nåede frem til den. Forskellige hypoteser er blevet udbudt gennem årene, men under alle omstændigheder hjalp Mercators venskab med Pedro Nunes og hans adgang til de loxodromiske borde, Nunes skabte, sandsynligvis til hjælp for hans indsats.

Den engelske matematiker Edward Wright offentliggjorde de første nøjagtige tabeller til konstruktion af projektionen i 1599 og mere detaljeret i 1610 og kaldte sin afhandling "Certaine Errors in Navigation". Den første matematiske formulering blev offentliggjort omkring 1645 af en matematiker ved navn Henry Bond (ca. 1600–1678). Imidlertid blev den involverede matematik udviklet, men aldrig udgivet af matematiker Thomas Harriot omkring 1589.

Udviklingen af ​​Mercator -projektionen repræsenterede et stort gennembrud i den nautiske kartografi fra 1500 -tallet. Det var imidlertid meget forud for sin tid, da de gamle navigations- og opmålingsteknikker ikke var forenelige med dets anvendelse i navigationen. To hovedproblemer forhindrede dens umiddelbare anvendelse: umuligheden af ​​at bestemme længdegraden til søs med tilstrækkelig nøjagtighed og det faktum, at magnetiske retninger i stedet for geografiske retninger blev brugt til navigation. Først i midten af ​​1700 -tallet, efter at det marine kronometer var opfundet, og den rumlige fordeling af magnetisk deklination var kendt, kunne Mercator -projektionen vedtages fuldt ud af navigatører.

På trods af disse begrænsninger til positionsbestemmelse kan Mercator-projektionen findes på mange verdenskort i århundrederne efter Mercators første udgivelse. Det begyndte imidlertid ikke at dominere verdenskort før i det 19. århundrede, da problemet med positionsbestemmelse stort set var blevet løst. Når Mercator blev den sædvanlige projektion for kommercielle og uddannelsesmæssige kort, blev den udsat for vedvarende kritik fra kartografer for dens ubalancerede repræsentation af landmasser og dens manglende evne til nyttig at vise polarområderne.

Kritikken mod uhensigtsmæssig brug af Mercator -projektionen resulterede i en strøm af nye opfindelser i slutningen af ​​det 19. og begyndelsen af ​​det 20. århundrede, ofte direkte fremført som alternativer til Mercator. På grund af dette pres reducerede forlagene gradvist deres brug af projektionen i løbet af det 20. århundrede. Fremkomsten af ​​webkortlægning gav imidlertid projektionen en brat genopblussen i form af Web Mercator -projektionen .

I dag kan Mercator findes i søkort, lejlighedsvise verdenskort og webkortlægningstjenester, men kommercielle atlas har stort set opgivet det, og vægkort over verden kan findes i mange alternative fremskrivninger. Google Maps , der har været afhængig af det siden 2005, bruger det stadig til lokalområder, men droppede projektionen fra desktop-platforme i 2017 for kort, der er zoomet ud af lokalområder. Mange andre online kortlægningstjenester bruger stadig udelukkende Web Mercator.

Ejendomme

Som i alle cylindriske fremskrivninger er paralleller og meridianer på Mercator lige og vinkelret på hinanden. Ved at opnå dette ledsages den uundgåelige øst -vest -strækning af kortet, der stiger, når afstanden fra ækvator øges, i Mercator -projektionen af ​​en tilsvarende nord -syd -strækning, således at øst -vest -skalaen ved hvert punkt er det samme som nord -syd skalaen, hvilket gør det til en konform kortprojektion . Konforme fremskrivninger bevarer vinkler rundt om alle steder.

Fordi den lineære skala på et Mercator -kort stiger med breddegraden, forvrænger størrelsen af ​​geografiske objekter langt fra ækvator og formidler en forvrænget opfattelse af planetens samlede geometri. På breddegrader større end 70 ° nord eller syd er Mercator -projektionen praktisk talt ubrugelig, fordi den lineære skala bliver uendeligt stor ved polerne. Et Mercator -kort kan derfor aldrig helt vise polarområderne (så længe projektionen er baseret på en cylinder centreret om Jordens rotationsakse; se den tværgående Mercator -projektion for en anden anvendelse).

Den mercatorprojektion knyttes alle linier med konstant bærende ( rhumbs (matematisk kendt som loxodromes-de making konstante vinkler med meridianer) og lige linjer De to egenskaber,. Tilpasningsevne og lige kompaslinjer, gør dette fremspring unikt egnet til marine navigation : kurser og lejer måles ved hjælp af vindroser eller vinkelmåler, og de tilsvarende retninger overføres let fra punkt til punkt på kortet ved hjælp af en parallel lineal (f.eks.).

Forvrængning af størrelser

Som på alle kortfremskrivninger er former eller størrelser forvrængninger af det sande layout af Jordens overflade.

Mercator -projektionen overdriver områder langt fra ækvator .

Eksempler på størrelsesforvrængning

• Antarktis ser ud til at være ekstremt stort. Hvis hele kloden blev kortlagt, ville Antarktis puste op i det uendelige. I virkeligheden er det det tredje mindste kontinent.

• Ellesmere Island på den nordlige del af Canada 's arktiske skærgård ser om det samme størrelse som Australien , selv om Australien er over 39 gange så stort. Alle øer i Canadas arktiske øhav ser mindst 4 gange for store ud, og de mere nordlige øer ser endnu større ud.

• Grønland ser ud til at have samme størrelse som Afrika , når Afrikas område i virkeligheden er 14 gange så stort.
  • Grønlands egentlige område kan sammenlignes med Den Demokratiske Republik Congo alene.
  • Afrika ser ud til at være nogenlunde samme størrelse som Sydamerika , når Afrika i virkeligheden er over halvanden gang så stort.

• Svalbard ser ud til at være større end Borneo , når Borneo i virkeligheden er omkring 12 gange så stor som Svalbard.

• Alaska ser ud til at have samme størrelse som Australien, selvom Australien faktisk er 4+1/2 gange så stort.
  • Alaska tager også lige så meget område på kortet som Brasilien , hvorimod Brasiliens område er næsten 5 gange Alaska.

• Madagaskar og Storbritannien ser omtrent samme størrelse ud, mens Madagaskar faktisk er mere end dobbelt så stort som den største af de britiske øer.
  • Sverige fremstår meget større end Madagaskar. I virkeligheden har de samme størrelse.

• Rusland fremstår større end hele Afrika eller Nordamerika (uden sidstnævntes øer). Det fremstår også dobbelt så stort som Kina og det sammenhængende USA tilsammen, når summen i virkeligheden er sammenlignelig i størrelse.
  • Den nordlige inflation forvrænger også akut Ruslands form, hvilket får den til at se meget højere ud fra nord til syd og strækker sine arktiske områder stærkt i forhold til dens midterste breddegrader.

Kritik

På grund af store forvrængninger af landarealet anser nogle fremskrivningen som uegnet til generelle verdenskort. Derfor brugte Mercator selv sinusformet projektion med lige område til at vise relative områder. På trods af sådanne forvrængninger var Mercator -projektionen, især i slutningen af ​​det 19. og begyndelsen af ​​det 20. århundrede, måske den mest almindelige projektion, der blev brugt i verdenskort, på trods af at den blev meget kritiseret for denne brug.

På grund af sin meget almindelige anvendelse har Mercator -projektionen formodes at have påvirket folks syn på verden, og fordi den viser lande i nærheden af ​​ækvator som for små i forhold til dem i Europa og Nordamerika, har den været formodet at forårsage mennesker at betragte disse lande som mindre vigtige. Som et resultat af denne kritik bruger moderne atlasser ikke længere Mercator-projektionen til verdenskort eller til områder fjernt fra ækvator, foretrækker andre cylindriske fremskrivninger eller former for projekter med lige areal . Mercator -projektionen bruges stadig stadig til områder nær ækvator, hvor forvrængning er minimal. Det findes også ofte på kort over tidszoner.

Arno Peters vakte kontroverser begyndende i 1972, da han foreslog, hvad der nu normalt kaldes Gall -Peters -projektionen for at afhjælpe Mercator -problemerne og hævdede, at det var hans eget originale værk uden at referere til tidligere arbejde af kartografer såsom Galls arbejde fra 1855. The projektion, han fremmede, er en specifik parameterisering af den cylindriske projektion med lige areal . Som svar blev en resolution fra 1989 af syv nordamerikanske geografiske grupper forringet ved hjælp af cylindriske fremskrivninger til verdenskort til generelle formål, som ville omfatte både Mercator og Gall-Peters.

Anvendelser

Næsten alle søkort i tryk er baseret på Mercator -projektionen på grund af dets unikke gunstige egenskaber til navigation. Det bruges også almindeligt af gadekorttjenester, der hostes på Internettet, på grund af dets enestående gunstige egenskaber for lokalområderskort beregnet efter behov. Mercator -fremskrivninger var også vigtige i den matematiske udvikling af pladetektonik i 1960'erne.

Marine navigation

Den mercatorprojektion er designet til anvendelse på havet navigation på grund af sin unikke egenskab at repræsentere nogen forløbet af konstant bærende som en lige segment. En sådan kurs, kendt som en rhumb (eller, matematisk, en loxodrome) foretrækkes inden for marinefart, fordi skibe kan sejle i en konstant kompasretning, hvilket reducerer de vanskelige, fejludsatte kursrettelser, der ellers ville være nødvendige ofte, når man sejler en anden Rute. For små afstande i forhold til jordens radius er forskellen mellem den rommelige og den teknisk korteste bane, et stort cirkelsegment , ubetydelig, og selv for længere afstande gør enkelheden af ​​det konstante leje det attraktivt. Som observeret af Mercator ville skibet på en sådan kurs ikke ankomme med den korteste rute, men det vil helt sikkert ankomme. At sejle en romb betød, at alt det søfolkene skulle gøre var at holde en konstant kurs, så længe de vidste, hvor de var, da de startede, hvor de havde tænkt sig at være, når de var færdige, og havde et kort i Mercator -projektion, der korrekt viste de to koordinater.

Web Mercator

Mange større online gademapningstjenester ( Bing Maps , Google Maps , Mapbox , MapQuest , OpenStreetMap , Yahoo! Maps og andre) bruger en variant af Mercator -projektionen til deres kortbilleder kaldet Web Mercator eller Google Web Mercator. På trods af sin variation indlysende skala på små skalaer, fremskrivningen er velegnet som et interaktivt verdenskort, der kan zoomes problemfrit til store (lokal) kortlægger, hvor der er relativt lidt forvrængning på grund af varianten projektion s nær- tilpasningsevne .

De store online gadekortlægningstjenesters flisebelægningssystemer viser det meste af verden på det laveste zoomniveau som et enkelt firkantet billede, eksklusive polarområderne ved afkortning på breddegrader på φ _max  = ± 85,05113 °. (Se nedenfor .) Latitudeværdier uden for dette område kortlægges ved hjælp af en anden relation, der ikke afviger ved  φ  = ± 90 °.

Matematik

Sfærisk model

Selvom Jordens overflade bedst modelleres af en oblat ellipsoid af revolution , er ellipsoiden tilnærmet til små skalaer af en sfære med radius a . Der findes mange forskellige metoder til beregning af a . Den enkleste omfatter (a) ellipsoidens ækvatorialradius, (b) det aritmetiske eller geometriske middel for ellipsoidens halvakser og (c) kuglens radius med samme volumen som ellipsoiden. Rækkevidden for a blandt de mulige valg er ca. 35 km, men for applikationer i lille skala (stor region) kan denne variation ignoreres, og middelværdier på 6.371 km og 40.030 km kan tages for henholdsvis radius og omkreds. Dette er de værdier, der bruges til numeriske eksempler i senere afsnit. Kun kartografi med stor nøjagtighed på store kort kræver en ellipsoid model.

Cylindriske fremspring

Den sfæriske tilnærmelse af Jorden med radius a kan modelleres af en mindre sfære af radius R , kaldet kloden i dette afsnit. Jordkloden bestemmer kortets skala. De forskellige cylindriske fremskrivninger angiver, hvordan de geografiske detaljer overføres fra kloden til en cylinder, der er tangential til den ved ækvator. Cylinderen rulles derefter ud for at give det plane kort. BrøkenR/-enkaldes den repræsentative fraktion (RF) eller projektionens hovedskala . For eksempel kan et Mercator -kort trykt i en bog have en ækvatorial bredde på 13,4 cm svarende til en globusradius på 2,13 cm og en RF på ca.1/300 mio (M bruges som en forkortelse for 1.000.000 ved at skrive en RF), mens Mercators originale 1569 -kort har en bredde på 198 cm svarende til en globusradius på 31,5 cm og en RF på ca. 1/20 mio.

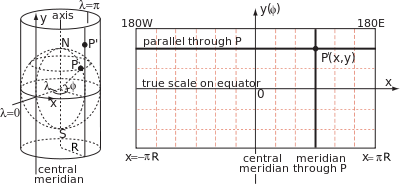
En cylindrisk kortfremskrivning er angivet ved formler, der forbinder de geografiske koordinater for breddegrad  φ og længdegrad  λ til kartesiske koordinater på kortet med oprindelse på ækvator og x -akse langs ækvator. Ved konstruktion ligger alle punkter på den samme meridian på cylinderens samme generator ved en konstant værdi på x , men afstanden y langs generatoren (målt fra ækvator) er en vilkårlig funktion af breddegrad, y ( φ ). Generelt beskriver denne funktion ikke den geometriske projektion (som af lysstråler på en skærm) fra midten af ​​kloden til cylinderen, som kun er en af ​​et ubegrænset antal måder til konceptuelt at projicere et cylindrisk kort.

Da cylinderen er tangential til kloden ved ækvator, er skalafaktoren mellem globus og cylinder enhed på ækvator, men ingen andre steder. Især da radius af en parallel eller breddegrundscirkel er R  cos  φ , skal den tilsvarende parallel på kortet have været strakt med en faktor på1/fordi φ= sek φ . Denne skalafaktor på parallellen betegnes konventionelt med k, og den tilsvarende skalafaktor på meridianen er angivet med  h .

Lille element geometri

Forholdet mellem y ( φ ) og projektionens egenskaber, såsom vinkeltransformation og variation i skala, følger af geometrien af ​​tilsvarende små elementer på kloden og kortet. Figuren herunder viser et punkt P på breddegrad  φ og længdegrad  λ på kloden og et nærliggende punkt Q på breddegrad φ  +  δφ og længdegrad λ  +  δλ . De lodrette linjer PK og MQ er buer af meridianer med længden Rδφ . De vandrette linjer PM og KQ er buer med paralleller med længden R (cos  φ ) δλ .

For små elementer er vinklen PKQ omtrent en ret vinkel og derfor

${\displaystyle \tan \alpha \approx {\frac {R\cos \varphi \,\delta \lambda }{R\,\delta \varphi }},\qquad \qquad \tan \beta ={\frac {\delta x}{\delta y}},}$

De tidligere nævnte skaleringsfaktorer fra globus til cylinder er givet af

parallel skala faktor     ${\displaystyle \quad k(\varphi )\;=\;{\frac {P'M'}{PM}}\;=\;{\frac {\delta x}{R\cos \varphi \,\delta \lambda }},}$

meridian skala faktor   ${\displaystyle \quad h(\varphi )\;=\;{\frac {P'K'}{PK}}\;=\;{\frac {\delta y}{R\delta \varphi \,}}.}$

Da meridianerne er kortlagt til linjer med konstant x , skal vi have x = R ( λ - λ ₀ ) og δx  =  Rδλ , ( λ i radianer). Derfor i grænsen for uendeligt små elementer

${\displaystyle \tan \beta ={\frac {R\sec \varphi }{y'(\varphi )}}\tan \alpha \,,\qquad k=\sec \varphi \,,\qquad h={\frac {y'(\varphi )}{R}}.}$

Afledning af Mercator -projektionen

Valget af funktionen y ( φ ) til Mercator -projektionen bestemmes af kravet om, at projektionen skal være konform, en betingelse, der kan defineres på to ækvivalente måder:

• Lighed med vinkler . Betingelsen om, at et sejlingsforløb med konstant azimut α på kloden er kortlagt til et konstant gitter, der bærer β på kortet. Indstilling α  =  β i ovenstående ligninger giver y ' ( φ ) =  R  sec  φ .
• Isotropi af skalafaktorer . Dette er udsagnet om, at punktskalafaktoren er uafhængig af retning, så små former bevares af projektionen. Indstilling h  =  k i ovenstående ligninger giver igen y ' ( φ ) =  R  sec  φ .

Integration af ligningen

${\displaystyle y'(\varphi )=R\sec \varphi ,}$

med y (0) = 0, ved hjælp af integrale tabeller eller elementære metoder , giver y (φ). Derfor,

${\displaystyle x=R(\lambda -\lambda _{0}),\qquad y=R\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right].}$

I den første ligning λ ₀ er længden af ​​en vilkårlig central meridian normalt, men ikke altid, Greenwich (dvs. nul). Forskellen ( λ  -  λ ₀ ) er i radianer.

Funktionen y ( φ ) er afbildet ved siden af φ for sagen R  = 1: den har tendens til uendelig ved polerne. De lineære y -akseværdier vises normalt ikke på trykte kort; i stedet viser nogle kort den ikke-lineære skala for breddegrader til højre. Oftere end ikke viser kortene kun en oversigt over udvalgte meridianer og paralleller

Omvendte transformationer

${\displaystyle \lambda =\lambda _{0}+{\frac {x}{R}},\qquad \varphi =2\tan ^{-1}\left[\exp \left({\frac {y}{R}}\right)\right]-{\frac {\pi }{2}}\,.}$

Udtrykket til højre for den anden ligning definerer den gudermannske funktion ; dvs. φ  = gd (y/R): den direkte ligning kan derfor skrives som y  =  R · gd ⁻¹ ( φ ).

Alternative udtryk

Der er mange alternative udtryk for y ( φ ), alle afledt af elementære manipulationer.

${\displaystyle {\begin{aligned}y&=&{\frac {R}{2}}\ln \left[{\frac {1+\sin \varphi }{1-\sin \varphi }}\right]&=&{R}\ln \left[{\frac {1+\sin \varphi }{\cos \varphi }}\right]&=R\ln \left(\sec \varphi +\tan \varphi \right)\\[2ex]&=&R\tanh ^{-1}\left(\sin \varphi \right)&=&R\sinh ^{-1}\left(\tan \varphi \right)&=R\operatorname {sgn} (\varphi )\cosh ^{-1}\left(\sec \varphi \right)=R\operatorname {gd} ^{-1}(\varphi ).\end{aligned}}}$

Tilsvarende inverser er:

${\displaystyle \varphi =\sin ^{-1}\left(\tanh {\frac {y}{R}}\right)=\tan ^{-1}\left(\sinh {\frac {y}{R}}\right)=\operatorname {sgn} (y)\sec ^{-1}\left(\cosh {\frac {y}{R}}\right)=\operatorname {gd} {\frac {y}{R}}.}$

For vinkler udtrykt i grader:

${\displaystyle x={\frac {\pi R(\lambda ^{\circ }-\lambda _{0}^{\circ })}{180}},\qquad \quad y=R\ln \left[\tan \left(45+{\frac {\varphi ^{\circ }}{2}}\right)\right].}$

De ovenstående formler er skrevet i form af kloden radius R . Det er ofte bekvemt at arbejde direkte med kortet bredde W  = 2 π R . For eksempel bliver de grundlæggende transformationsligninger

${\displaystyle x={\frac {W}{2\pi }}\left(\lambda -\lambda _{0}\right),\qquad \quad y={\frac {W}{2\pi }}\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right].}$

Afkortning og billedformat

Ordinaten y for Mercator -projektionen bliver uendelig ved polerne, og kortet skal afkortes på en breddegrad mindre end halvfems grader. Dette behøver ikke at ske symmetrisk. Mercators originale kort er afkortet ved 80 ° N og 66 ° S med det resultat, at europæiske lande blev flyttet mod midten af ​​kortet. Den skærmformat af hans kort er198/120= 1,65. Endnu mere ekstreme afkortninger er blevet brugt: Et finsk skoleatlas blev afkortet ved cirka 76 ° N og 56 ° S, et billedformat på 1,97.

Meget webbaseret kortlægning bruger en zoombar version af Mercator-projektionen med et billedformat på en. I dette tilfælde skal den opnåede maksimale breddegrad svare til y  = ±W/2eller tilsvarende y/R =  π . Enhver af de inverse transformationsformler kan bruges til at beregne de tilsvarende breddegrader:

${\displaystyle \varphi =\tan ^{-1}\left[\sinh \left({\frac {y}{R}}\right)\right]=\tan ^{-1}\left[\sinh \pi \right]=\tan ^{-1}\left[11.5487\right]=85.05113^{\circ }.}$

Skaleringsfaktor

Den figur sammenligne uendeligt elementer på globe og fremskrivning viser, at når α = β trekanterne PQM og P'Q'M 'er ens, således at skaleringsfaktoren i en vilkårlig retning er den samme som den parallelle og skalafaktorer meridian:

${\displaystyle {\frac {\delta s'}{\delta s}}={\frac {P'Q'}{PQ}}={\frac {P'M'}{PM}}=k={\frac {P'K'}{PK}}=h=\sec \varphi .}$

Dette resultat gælder for en vilkårlig retning: definitionen af isotropi af punktskalafaktoren . Grafen viser variationen af ​​skalafaktoren med breddegrad. Nogle numeriske værdier er angivet nedenfor.

ved breddegrad 30 ° er skalafaktoren   k  = sek 30 ° = 1,15,

på breddegrad 45 ° er skalafaktoren   k  = sek 45 ° = 1,41,

på breddegraden 60 ° er skalafaktoren   k  = sek 60 ° = 2,

ved breddegrad 80 ° er skalafaktoren   k  = sek 80 ° = 5,76,

på breddegrad 85 ° er skalafaktoren   k  = sek 85 ° = 11,5

At arbejde ud fra det projicerede kort kræver skalafaktoren i henhold til Mercator -ordinaten y (medmindre kortet er forsynet med en eksplicit breddegrad). Da linealmålinger kan give kortets ordinat y og også bredden W af kortet dengangy/R = 2 πy/W og skalafaktoren bestemmes ved hjælp af en af ​​de alternative former for formerne for den inverse transformation:

${\displaystyle k=\sec \varphi =\cosh \left({\frac {y}{R}}\right)=\cosh \left({\frac {2\pi y}{W}}\right).}$

Variationen med breddegrad er undertiden angivet med flere stregskalaer som vist herunder og for eksempel på et finsk skoleatlas . Fortolkningen af ​​sådanne stangvægte er ikke-triviel. Se diskussionen om afstandsformler herunder.

Områdeskala

Arealskalafaktoren er produktet af parallel- og meridianskalaerne hk = sek ² φ . For Grønland med 73 ° som en median breddegrad, hk = 11,7. For Australien med 25 ° som en median breddegrad, hk = 1,2. For Storbritannien med 55 ° som en median breddegrad, hk = 3,04.

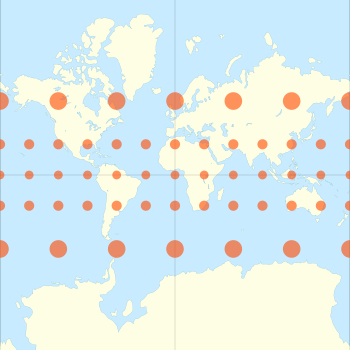
Forvrængning

Den klassiske måde at vise den forvrængning, der er forbundet med en projektion, er at bruge Tissots indikatrix . Nicolas Tissot bemærkede, at skalafaktorerne på et punkt på en kortfremvisning, angivet med tallene h og k , definerer en ellipse på det tidspunkt. Ved cylindriske fremspring er ellipsens akser tilpasset meridianerne og parallellerne. For Mercator -projektionen, h  =  k , så ellipserne degenererer til cirkler med en radius, der er proportional med værdien af ​​skalafaktoren for denne breddegrad. Disse cirkler gengives på det projicerede kort med ekstrem variation i størrelse, hvilket er tegn på Mercators skalavariationer.

Nøjagtighed

Et mål for kortets nøjagtighed er en sammenligning af længden af ​​de tilsvarende linjeelementer på kortet og kloden. Derfor er Mercator -projektionen ved konstruktion helt præcis, k  = 1, langs ækvator og ingen andre steder. På en breddegrad på ± 25 ° er værdien af ​​sek  φ omkring 1,1, og derfor kan fremskrivningen anses for at være nøjagtig til inden for 10% i en strimmel med en bredde på 50 ° centreret på ækvator. Smalere strimler er bedre: sek 8 ° = 1,01, så en strimmel med bredde 16 ° (centreret på ækvator) er præcis til inden for 1% eller 1 del i 100. Tilsvarende sek 2,56 ° = 1,001, så en strimmel med bredde 5,12 ° (centreret på ækvator) er nøjagtig til inden for 0,1% eller 1 del i 1.000. Derfor er Mercator -projektionen tilstrækkelig til at kortlægge lande tæt på ækvator.

Sikker projektion

I en sekant (i form af skæring) Mercator -projektion projiceres kloden til en cylinder, der skærer kuglen i to paralleller med breddegrader ± φ ₁ . Skalaen er nu sand på disse breddegrader, mens paralleller mellem disse breddegrader er kontraheret af projektionen, og deres skalafaktor skal være mindre end en. Resultatet er, at afvigelsen af skalaen fra enhed reduceres over et bredere område af breddegrader.

Et eksempel på en sådan fremskrivning er

${\displaystyle x=0.99R\lambda \qquad y=0.99R\ln \tan \!\left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\qquad k\;=0.99\sec \varphi .}$

Skalaen på ækvator er 0,99; skalaen er k  = 1 på en breddegrad på ca. ± 8 ° (værdien på φ ₁ ); skalaen er k  = 1,01 på en breddegrad på cirka ± 11,4 °. Derfor har projektionen en nøjagtighed på 1%over en bredere strimmel på 22 ° sammenlignet med 16 ° for den normale (tangent) projektion. Dette er en standardteknik til at udvide det område, over hvilket et kortprojektion har en given nøjagtighed.

Generalisering til ellipsoiden

Når Jorden er modelleret af en sfæroid ( ellipsoid af revolution) skal Mercator -projektionen ændres, hvis den skal forblive i overensstemmelse . Transformationsligningerne og skalafaktoren for den ikke-sekant version er

Skalafaktoren er enhed på ækvator, som den må være, da cylinderen er tangential til ellipsoiden ved ækvator. Den ellipsoide korrektion af skalafaktoren stiger med breddegraden, men den er aldrig større end e ² , en korrektion på mindre end 1%. (Værdien af e ² er omkring 0,006 for alle referenceelipsoider.) Dette er meget mindre end skalaens unøjagtighed, undtagen meget tæt på ækvator. Kun nøjagtige Mercator -fremskrivninger af regioner nær ækvator vil nødvendiggøre ellipsoide korrektioner.

Det omvendte løses iterativt, da den isometriske breddegrad er involveret.

Formler til afstand

Konvertering af linealafstand på Mercator -kortet til sand ( stor cirkel ) afstand på kuglen er ligetil langs ækvator, men ingen andre steder. Et problem er variationen af ​​skalaen med breddegrad, og et andet er, at lige linjer på kortet ( rumlinjer ), bortset fra meridianerne eller ækvator, ikke svarer til store cirkler.

Sondringen mellem rhumb (sejlende) afstand og stor cirkel (sand) afstand blev klart forstået af Mercator. (Se forklaring 12 på 1569 -kortet.) Han understregede, at afstanden mellem linjeformede linier er en acceptabel tilnærmelse til sand stor cirkelafstand for kurser med kort eller moderat afstand, især på lavere breddegrader. Han kvantificerer endda sit udsagn: "Når de store cirkeldistancer, der skal måles i nærheden af ​​ækvator, ikke overstiger 20 grader af en stor cirkel eller 15 grader nær Spanien og Frankrig, eller 8 og endda 10 grader i nordlige dele det er praktisk at bruge rhumb line -afstande ".

Til en linealmåling af en kort linje, med midtpunkt på breddegrad  φ , hvor skalafaktoren er k  = sek  φ  = 1/fordi  φ:

Sand afstand = rumafstand ≅ linealafstand × cos  φ / RF. (korte linjer)

Med radius og stor cirkelomkreds svarende til henholdsvis 6.371 km og 40.030 km en RF på 1/300 mio, for hvilke R  = 2,12 cm og B  = 13,34 cm, indebærer, at en lineal måler 3 mm. i enhver retning fra et punkt på ækvator svarer til cirka 900 km. De tilsvarende afstande for breddegrader 20 °, 40 °, 60 ° og 80 ° er henholdsvis 846 km, 689 km, 450 km og 156 km.

Længere afstande kræver forskellige tilgange.

På ækvator

Skala er enhed på ækvator (for en ikke-sekant projektion). Derfor er fortolkning af linealmålinger på ækvator enkel:

Sand afstand = linealafstand / RF (ækvator)

For ovenstående model, med RF = 1/300 mio, 1 cm svarer til 3.000 km.

På andre paralleller

På enhver anden parallel er skalafaktoren sek φ så at

Parallel afstand = linealafstand × cos  φ / RF (parallel).

For ovenstående model svarer 1 cm til 1.500 km på en breddegrad på 60 °.

Dette er ikke den korteste afstand mellem de valgte slutpunkter på parallellen, fordi en parallel ikke er en stor cirkel. Forskellen er lille for korte afstande, men stiger, når λ , den langsgående adskillelse, stiger. For to punkter, A og B, adskilt af 10 ° længdegrad på parallellen ved 60 ° er afstanden langs parallellen cirka 0,5 km større end den store cirkeldistance. (Afstanden AB langs parallellen er ( en  cos  φ )  λ . Længden af ​​akkorden AB er 2 ( en  cos  φ ) sin λ/2. Denne akkord underkaster en vinkel i midten lig med 2arcsin (cos  φ  sin λ/2) og den store cirkelafstand mellem A og B er 2 en  buesin (cos  φ  sin λ/2).)) I ekstreme tilfælde, hvor længdeseparationen er 180 °, er afstanden langs parallellen den ene halvdel af omkredsen af ​​denne parallel; dvs. 10,007,5 km. På den anden side er den geodesiske mellem disse punkter en stor cirkelbue gennem polen, der bøjer en vinkel på 60 ° i midten: længden af ​​denne bue er en sjettedel af den store cirkelomkreds, cirka 6.672 km. Forskellen er 3.338 km, så linealafstanden målt fra kortet er ret vildledende, selv efter at der er korrigeret for skalafaktorens breddegradvariation.

På en meridian

En meridian på kortet er en stor cirkel på kloden, men den kontinuerlige skalavariation betyder, at linealmåling alene ikke kan give den sande afstand mellem fjerne punkter på meridianen. Men hvis kortet er markeret med en nøjagtig og fint fordelt breddegradskala, hvorfra breddegraden kan læses direkte - som det er tilfældet med Mercator 1569 -verdenskortet (ark 3, 9, 15) og alle efterfølgende søkort - meridianen afstanden mellem to breddegrader φ ₁ og φ ₂ er ganske enkelt

${\displaystyle m_{12}=a|\varphi _{1}-\varphi _{2}|.}$

Hvis slutpunkternes breddegrader ikke kan bestemmes med tillid, kan de i stedet findes ved beregning af linealafstanden. Ved at kalde linealafstandene for slutpunkterne på kortmeridianen målt fra ækvator y ₁ og y ₂ , er den sande afstand mellem disse punkter på kuglen givet ved at bruge en af ​​de inverse Mercator -formler:

${\displaystyle m_{12}=a\left|\tan ^{-1}\left[\sinh \left({\frac {y_{1}}{R}}\right)\right]-\tan ^{-1}\left[\sinh \left({\frac {y_{2}}{R}}\right)\right]\right|,}$

hvor R kan beregnes ud fra bredden W på kortet med R  = W/2 π. For eksempel på et kort med R  = 1  svarer værdierne for y = 0, 1, 2, 3 til breddegrader på φ  = 0 °, 50 °, 75 °, 84 ° og derfor de successive intervaller på 1 cm på kortet svarer til breddegradsintervaller på kloden 50 °, 25 °, 9 ° og afstande på 5.560 km, 2.780 km og 1.000 km på Jorden.

På en rhumb

En lige linje på Mercator -kortet i vinkel α til meridianerne er en fast linie . Når α  = π/2 eller 3 π/2rimen svarer til en af ​​parallellerne; kun den ene, ækvator, er en stor cirkel. Når α  = 0 eller π svarer det til en meridian stor cirkel (hvis den fortsættes rundt om Jorden). For alle andre værdier er det en spiral fra pol til pol på kloden, der skærer alle meridianer i samme vinkel, og er dermed ikke en stor cirkel. Dette afsnit diskuterer kun den sidste af disse sager.

Hvis α hverken er 0 eller π, viser ovenstående figur af de uendelige elementer, at længden af ​​en uendelig lille linie på kuglen mellem breddegrader φ ; og φ  +  δφ er et  sekund  α  δφ . Da α er konstant på rammen, kan dette udtryk integreres for at give, for endelige linjer på jorden:

${\displaystyle r_{12}=a\sec \alpha \,|\varphi _{1}-\varphi _{2}|=a\,\sec \alpha \;\Delta \varphi .}$

Endnu en gang, hvis Δ φ kan læses direkte fra en nøjagtig breddegradskala på kortet, er afstanden mellem kortpunkter med kortpunkterne φ ₁ og φ ₂ givet ved ovenstående. Hvis der ikke er en sådan skala, giver linealen afstand mellem slutpunkterne og ækvator, y ₁ og y ₂ , resultatet via en invers formel:

${\displaystyle r_{12}=a\sec \alpha \left|\tan ^{-1}\sinh \left({\frac {y_{1}}{R}}\right)-\tan ^{-1}\sinh \left({\frac {y_{2}}{R}}\right)\right|.}$

Disse formler giver rumafstande på sfæren, som kan afvige meget fra sande afstande, hvis bestemmelse kræver mere sofistikerede beregninger.

Se også

• Kartografi
• Central cylindrisk projektion - mere forvrænget; undertiden fejlagtigt beskrevet som metoden til konstruktion af Mercator -projektionen
• Konform kortprojektion
• Lige-kantet projektion -mindre forvrænget, men ikke lige område
• Gall – Peters projektion -et cylindrisk projektion med lige areal
• Jordan tværgående Mercator
• Liste over kortfremskrivninger
• Mercator 1569 verdenskort
• Søkort
• Rhumbline netværk
• Tissots indikator
• Tværgående Mercator projektion
• Universal tværgående Mercator koordinatsystem

Noter

Referencer

Bibliografi

• Maling, Derek Hylton (1992), Coordinate Systems and Map Projections (anden udgave), Pergamon Press, ISBN 0-08-037233-3.
• Monmonier, Mark (2004), Rhumb Lines and Map Wars: A Social History of the Mercator Projection (Hardcover ed.), Chicago: The University of Chicago Press, ISBN 0-226-53431-6
• Olver, FWJ; Lozier, DW; Boisvert, RF; et al., red. (2010), NIST Handbook of Mathematical Functions , Cambridge University Press
• Osborne, Peter (2013), The Mercator Projections , doi : 10.5281/zenodo.35392 . (Tillæg: Maxima -filer og Latex -kode og tal )CS1 maint: postscript (link)
• Snyder, John P (1993), Flattening the Earth: Two Thousand Years of Map Projections , University of Chicago Press, ISBN 0-226-76747-7
• Snyder, John P. (1987), Map Projections - A Working Manual. US Geological Survey Professional Paper 1395 , United States Government Printing Office, Washington, DCDette papir kan downloades fra USGS -sider. Det giver fuldstændige detaljer om de fleste fremskrivninger sammen med interessante indledende afsnit, men det stammer ikke fra projekterne fra de første principper.

Yderligere læsning

• Rapp, Richard H (1991), Geometrisk Geodæsi, del I , Ohio State University Institut for Geodætisk Videnskab og opmåling, HDL : 1811/24333

eksterne links

• Ad maiorem Gerardi Mercatoris gloriam -indeholder billeder i høj opløsning af verdenskortet fra 1569 af Mercator.
• Tabel over eksempler og egenskaber for alle almindelige fremskrivninger , fra radicalcartography.net.
• En interaktiv Java Applet til at studere de metriske deformationer af Mercator -projektionen .
• Web Mercator: Ikke-konform, ikke-Mercator (Noel Zinn, Hydrometronics LLC)
• Mercators projektion ved University of British Columbia
• Google Maps -koordinater