Lodret trykvariation - Vertical pressure variation

Lodret trykvariation er variationen i tryk som en funktion af højde . Afhængig af den pågældende væske og den sammenhæng, der henvises til, kan den også variere betydeligt i dimensioner vinkelret på højden, og disse variationer har relevans i sammenhæng med trykgradientkraft og dens virkninger. Den lodrette variation er imidlertid særlig signifikant, da den skyldes tyngdekraften på væsken; nemlig for den samme givne væske svarer et fald i højden i den til en højere væskesøjle, der vejer ned på dette punkt.

Grundformel

En relativt enkel version af den lodrette fluidtryksvariation er simpelthen, at trykforskellen mellem to højder er produktet af højdeforandring, tyngdekraft og tæthed . Ligningen er som følger:

${\ displaystyle {\ frac {dP} {dh}} = - \ rho g}$ og

hvor

P er tryk,

ρ er densitet,

g er tyngdeacceleration , og

h er højde.

Delta-symbolet angiver en ændring i en given variabel. Da g er negativ, vil en stigning i højden svare til et fald i tryk, hvilket passer med den tidligere nævnte begrundelse for vægten af ​​en væskesøjle.

Når tæthed og tyngdekraft er omtrent konstant (det vil sige for relativt små ændringer i højden), vil simpelthen multiplicering af højdeforskel, tyngdekraft og densitet give en god tilnærmelse af trykforskellen. Hvor forskellige væsker er lagdelt oven på hinanden, opnås den samlede trykforskel ved at tilføje de to trykforskelle; den første er fra punkt 1 til grænsen, den anden er fra grænsen til punkt 2; hvilket ville bare indebære erstatte ρ og A h værdier for hver væske og tage summen af resultaterne. Hvis væskens densitet varierer med højden, ville matematisk integration være påkrævet.

Hvorvidt tæthed og tyngdekraft med rimelighed kan tilnærmes som konstant, afhænger af det nødvendige nøjagtighedsniveau , men også af længdeskalaen for højdeforskellen, da tyngdekraften og densiteten også falder med højere højde. Især med hensyn til densitet er den pågældende væske også relevant; havvand betragtes for eksempel som en ukomprimerbar væske ; dens densitet kan variere med højden, men meget mindre markant end luftens. Således kan vandtætheden tilnærmes mere med rimelighed som konstant end luftens, og givet den samme højdeforskel er trykforskellene i vand omtrent ens i enhver højde.

Hydrostatisk paradoks

Den barometriske formel afhænger kun af væskekammerets højde og ikke af bredden eller længden. I betragtning af en stor nok højde kan ethvert tryk nås. Denne egenskab ved hydrostatik er blevet kaldt det hydrostatiske paradoks . Som udtrykt af WH Besant ,

Enhver mængde væske, uanset hvor lille den er, kan fremstilles til at bære enhver vægt, uanset hvor stor.

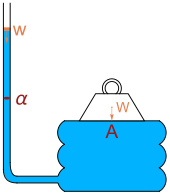
Den hollandske videnskabsmand Simon Stevin var den første til at forklare paradokset matematisk. I 1916 nævnte Richard Glazebrook det hydrostatiske paradoks, da han beskrev et arrangement, han tilskrev Pascal : en tung vægt W hviler på et bræt med område A, der hviler på en væskeblære forbundet med et lodret rør med tværsnitsareal α. Hælde vand af vægt w ned i røret vil til sidst hæve den tunge vægt. Balance mellem kræfter fører til ligningen

${\ displaystyle W = {\ frac {wA} {\ alpha}}.}$

Glazebrook siger, "Ved at gøre brættets areal betydeligt og det for røret lille, kan en stor vægt W understøttes af en lille vægt w vand. Denne kendsgerning beskrives undertiden som det hydrostatiske paradoks."

Demonstrationer af det hydrostatiske paradoks bruges til at undervise i fænomenet.

I sammenhæng med Jordens atmosfære

Hvis man skal analysere den lodrette trykvariation af jordens atmosfære , er længdeskalaen meget signifikant ( troposfæren alene er flere kilometer høj, termosfæren er flere hundrede kilometer), og den involverede væske (luft) er komprimerbar. Tyngdekraften kan stadig med rimelighed tilnærmes som konstant, fordi længdeskalaer i størrelsesordenen kilometer stadig er små i forhold til Jordens radius, som i gennemsnit er ca. 6371 km, og tyngdekraften er en funktion af afstanden fra Jordens kerne.

Densitet varierer derimod mere markant med højden. Det følger af den ideelle gaslov, at

${\ displaystyle \ rho = {\ frac {mP} {kT}},}$

hvor

m er gennemsnitlig masse pr. luftmolekyle ,

P er tryk ved et givet punkt,

k er Boltzmann-konstanten ,

T er temperaturen i kelvin .

Mere enkelt sagt afhænger lufttætheden af ​​lufttrykket. I betragtning af at lufttrykket også afhænger af lufttætheden, ville det være let at få det indtryk, at dette var en cirkulær definition , men det er simpelthen indbyrdes afhængighed af forskellige variabler. Dette giver derefter en mere nøjagtig formel af formularen

${\ displaystyle P_ {h} = P_ {0} e ^ {- {\ frac {mgh} {kT}},}$

hvor

P _h er trykket ved højden h ,

P ₀ er trykket ved referencepunkt 0 (typisk henvisning til havets overflade),

m er massen pr. luftmolekyle,

g er accelerationen på grund af tyngdekraften ,

h er højde fra referencepunkt 0,

k er Boltzmann-konstanten ,

T er temperaturen i kelvin.

Derfor er det i stedet for at være en lineær højdefunktion, som man kunne forvente af den mere enkle formel, der er givet i afsnittet "grundformel", mere nøjagtigt repræsenteret som en eksponentiel funktion af højden.

Bemærk, at i denne forenkling behandles temperaturen som konstant, selvom temperaturen også varierer med højden. Imidlertid er temperaturvariationen i de nedre lag af atmosfæren ( troposfæren , stratosfæren ) kun i snesevis af grader i modsætning til deres termodynamiske temperatur , som er i hundrederne, så temperaturvariationen er rimelig lille og ignoreres således. For mindre højdeforskelle, inklusive dem fra top til bund af selv de højeste bygninger (som CN-tårnet ) eller for bjerge af sammenlignelig størrelse, vil temperaturvariationen let være inden for enkeltcifrene. (Se også bortfaldsrate .)

En alternativ afledning, vist af Portland State Aerospace Society, bruges til at give højde som en funktion af tryk i stedet. Dette kan virke kontraintuitivt, da tryk skyldes højde snarere end omvendt, men en sådan formel kan være nyttig til at finde højde baseret på trykforskel, når man kender sidstnævnte og ikke førstnævnte. Forskellige formler præsenteres for forskellige slags tilnærmelser; til sammenligning med den foregående formel vil den første henvist fra artiklen være den, der anvender den samme tilnærmelse med konstant temperatur; i hvilket tilfælde:

${\ displaystyle z = - {\ frac {RT} {g}} \ ln {\ frac {P} {P_ {0}}}}$

hvor (med værdier brugt i artiklen)

z er højden i meter,

R er den specifikke gaskonstant = 287.053 J / (kg K)

T er den absolutte temperatur i kelvin = 288,15 K ved havoverfladen,

g er accelerationen på grund af tyngdekraften = 9.806 65  m / s ² ved havoverfladen,

P er trykket ved et givet punkt ved højde z i Pascals , og

P ₀ er tryk ved referencepunktet = 101.325 Pa ved havoverfladen.

En mere generel formel afledt i den samme artikel tegner sig for en lineær ændring i temperaturen som en funktion af højden (bortfaldshastighed) og reduceres til over, når temperaturen er konstant:

${\ displaystyle z = {\ frac {T_ {0}} {L}} \ left (\ left ({\ frac {P} {P_ {0}}} \ right) ^ {- {\ frac {LR} { g}}} - 1 \ højre)}$

hvor

L er den atmosfæriske bortfaldshastighed (temperaturændring divideret med afstand) = −6,5 × 10 ⁻³  K / m , og

T ₀ er temperaturen ved samme referencepunkt for hvilke P = P ₀

og de andre mængder er de samme som ovenfor. Dette er den anbefalede formel, der skal bruges.

Se også

• Barometer
• Hypsometrisk ligning
• Pascals tønde
• Ruina montium
• Trykgradient
• Sifon

Referencer

• Merlino, Robert L. (2003). "Statik - Væsker i hvile" . Hentet 2014-11-20 .