Elliptisk integral - Elliptic integral

I integralregning er en elliptisk integral en af ​​et antal relaterede funktioner defineret som værdien af ​​visse integraler. Oprindeligt opstod de i forbindelse med problemet med at finde en ellipses buelængde og blev først undersøgt af Giulio Fagnano og Leonhard Euler ( ca.  1750 ). Moderne matematik definerer en "elliptisk integral" som enhver funktion f, som kan udtrykkes i formen

${\ displaystyle f (x) = \ int _ {c} ^ {x} R \ left (t, {\ sqrt {P (t)}} \ right) \, \ mathrm {d} t,}$

hvor R er en rationel funktion af sine to argumenter, er P et polynom af grad 3 eller 4 uden gentagne rødder, og c er en konstant.

Generelt kan integraler i denne form ikke udtrykkes i form af elementære funktioner . Undtagelser fra denne generelle regel er, når P har gentagne rødder, eller når R ( x , y ) ikke indeholder mærkelige kræfter for y . Men med den passende reduktionsformel kan hver elliptisk integral bringes i en form, der involverer integraler over rationelle funktioner og de tre Legendre-kanoniske former (dvs. de elliptiske integraler af den første, anden og tredje slags).

Udover Legendre-formen nedenfor, kan de elliptiske integraler også udtrykkes i Carlson symmetrisk form . Yderligere indsigt i teorien om den elliptiske integral kan opnås gennem studiet af kortlægningen Schwarz – Christoffel . Historisk blev elliptiske funktioner opdaget som inverse funktioner af elliptiske integraler.

Argumentnotation

Ufuldstændige elliptiske integraler er funktioner i to argumenter; komplette elliptiske integraler er funktioner i et enkelt argument. Disse argumenter udtrykkes på en række forskellige, men ækvivalente måder (de giver den samme elliptiske integral). De fleste tekster overholder et kanonisk navneskema ved hjælp af følgende navngivningskonventioner.

For at udtrykke et argument:

• α , den modulære vinkel
• k = sin α , den elliptiske modul eller excentricitet
• m = k ² = sin ² α , parameteren

Hver af de ovennævnte tre størrelser bestemmes fuldstændigt af nogen af ​​de andre (givet at de ikke er negative). Således kan de bruges om hverandre.

Det andet argument kan ligeledes udtrykkes som φ , amplituden eller som x eller u , hvor x = sin φ = sn u og sn er en af ​​de Jacobianske elliptiske funktioner .

Angivelse af værdien af ​​en af ​​disse størrelser bestemmer de andre. Bemærk, at u også afhænger af m . Nogle yderligere forhold, der involverer u, inkluderer

${\ displaystyle \ cos \ varphi = \ operatorname {cn} u, \ quad {\ textrm {and}} \ quad {\ sqrt {1-m \ sin ^ {2} \ varphi}} = \ operatorname {dn} u .}$

Sidstnævnte kaldes undertiden delta-amplitude og skrives som Δ ( φ ) = dn u . Undertiden refererer litteraturen også til den komplementære parameter , den komplementære modul eller den komplementære modulære vinkel . Disse er nærmere defineret i artiklen om kvartalsperioder .

Ufuldstændig elliptisk integral af den første slags

Den ufuldstændige elliptiske integral af den første slags F defineres som

${\ displaystyle F (\ varphi, k) = F \ left (\ varphi \ mid k ^ {2} \ right) = F (\ sin \ varphi; k) = \ int _ {0} ^ {\ varphi} { \ frac {\ mathrm {d} \ theta} {\ sqrt {1-k ^ {2} \ sin ^ {2} \ theta}}.}$

Dette er den trigonometriske form for integralet; Ved at erstatte t = sin θ og x = sin φ opnår man Legendre normal form:

${\ displaystyle F (x; k) = \ int _ {0} ^ {x} {\ frac {\ mathrm {d} t} {\ sqrt {\ left (1-t ^ {2} \ right) \ left (1-k ^ {2} t ^ {2} \ højre)}}}.}$

Tilsvarende har man med hensyn til amplitude og modulvinkel:

${\ displaystyle F (\ varphi \ setminus \ alpha) = F (\ varphi, \ sin \ alpha) = \ int _ {0} ^ {\ varphi} {\ frac {\ mathrm {d} \ theta} {\ sqrt {1 - (\ sin \ theta \ sin \ alpha) ^ {2}}}}.}$

I denne notation angiver brugen af ​​en lodret bjælke som afgrænser, at argumentet, der følger den, er "parameteren" (som defineret ovenfor), mens backslash indikerer, at det er den modulære vinkel. Brugen af ​​semikolon indebærer, at argumentet, der går forud for det, er amplitudens sinus:

${\ displaystyle F (\ varphi, \ sin \ alpha) = F \ left (\ varphi \ mid \ sin ^ {2} \ alpha \ right) = F (\ varphi \ setminus \ alpha) = F (\ sin \ varphi ; \ sin \ alpha).}$

Denne potentielt forvirrende brug af forskellige argumentafgrænsere er traditionel i elliptiske integraler, og meget af notationen er kompatibel med den, der er brugt i referencebogen af Abramowitz og Stegun, og den, der bruges i de integrerede tabeller af Gradshteyn og Ryzhik .

Med x = sn ( u , k ) har man:

${\ displaystyle F (x; k) = u;}$

således er de Jacobianske elliptiske funktioner inverser til de elliptiske integraler.

Den ufuldstændige elliptiske integral af den første art har følgende tilføjelsessætning:

${\ displaystyle F [\ arctan (x), k] + F [\ arctan (y), k] = F \ left [\ arctan \ left ({\ frac {x {\ sqrt {k '^ {2} y ^ {2} +1}}} {\ sqrt {y ^ {2} +1}}} \ højre) + \ arctan \ left ({\ frac {y {\ sqrt {k '^ {2} x ^ { 2} +1}}} {\ sqrt {x ^ {2} +1}}} højre), k \ højre]}$

Den elliptiske modul kan transformeres på den måde:

${\ displaystyle F [\ arcsin (x), k] = {\ frac {2} {1 + {\ sqrt {1-k ^ {2}}}}} F \ left [\ arcsin \ left [{\ frac {(1 + {\ sqrt {1-k ^ {2}}}) x} {1 + {\ sqrt {1-k ^ {2} x ^ {2}}}} \ højre], {\ frac {1 - {\ sqrt {1-k ^ {2}}}} {1 + {\ sqrt {1-k ^ {2}}}} \ højre]}$

Notationsvarianter

Der er stadig andre konventioner til notering af elliptiske integraler anvendt i litteraturen. Notationen med udskiftede argumenter, F ( k , φ ) , findes ofte; og ligeledes E ( k , φ ) for integralen af ​​den anden art. Abramowitz og Stegun erstatter integralet af den første slags, F ( φ , k ) , for argumentet φ i deres definition af integralerne af anden og tredje slags, medmindre dette argument efterfølges af en lodret bjælke: dvs. E ( F ( φ , k ) | k ² ) for E ( φ | k ² ) . Desuden deres fuldstændige integraler ansætte parameter k ² som argument i stedet for modul k , dvs. K ( k ² ) snarere end K ( k ) . Og integralet af den tredje slags defineret af Gradshteyn og Ryzhik , Π ( φ , n , k ) , sætter amplituden φ først og ikke den "karakteristiske" n .

Man skal således være forsigtig med notationen, når man bruger disse funktioner, fordi forskellige velrenommerede referencer og softwarepakker bruger forskellige konventioner i definitionerne af de elliptiske funktioner. For eksempel definerer nogle referencer og Wolfram 's Mathematica software og Wolfram Alpha den komplette elliptiske integral af den første slags med hensyn til parameteren m i stedet for den elliptiske modul k .

${\ displaystyle K (m) = \ int _ {0} ^ {\ tfrac {\ pi} {2}} {\ frac {\ mathrm {d} \ theta} {\ sqrt {1-m \ sin ^ {2 } \ theta}}}}$

Ufuldstændig elliptisk integral af anden slags

Den ufuldstændige elliptiske integral af den anden slags E i trigonometrisk form er

${\ displaystyle E (\ varphi, k) = E \ left (\ varphi \, | \, k ^ {2} \ right) = E (\ sin \ varphi; k) = \ int _ {0} ^ {\ varphi} {\ sqrt {1-k ^ {2} \ sin ^ {2} \ theta}} \, \ mathrm {d} \ theta.}$

Ved at erstatte t = sin θ og x = sin φ opnår man Legendres normale form:

${\ displaystyle E (x; k) = \ int _ {0} ^ {x} {\ frac {\ sqrt {1-k ^ {2} t ^ {2}}} {\ sqrt {1-t ^ { 2}}}} \, \ mathrm {d} t.}$

Tilsvarende med hensyn til amplitude og modulvinkel:

${\ displaystyle E (\ varphi \ setminus \ alpha) = E (\ varphi, \ sin \ alpha) = \ int _ {0} ^ {\ varphi} {\ sqrt {1- \ left (\ sin \ theta \ sin \ alpha \ right) ^ {2}}} \, \ mathrm {d} \ theta.}$

Forholdet til Jacobi elliptiske funktioner inkluderer

${\ displaystyle E {\ bigl (} \ operatorname {sn} (u; k); k {\ bigr)} = \ int _ {0} ^ {u} \ operatorname {dn} ^ {2} (w; k ) \, \ mathrm {d} w = uk ^ {2} \ int _ {0} ^ {u} \ operatorname {sn} ^ {2} (w; k) \, \ mathrm {d} w = \ left (1-k ^ {2} \ højre) u + k ^ {2} \ int _ {0} ^ {u} \ operatornavn {cn} ^ {2} (w; k) \, \ mathrm {d} w .}$

Den meridianen bue længden fra ækvator til breddegrad φ er skrevet i form af E :

${\ displaystyle m (\ varphi) = a \ left (E (\ varphi, e) + {\ frac {\ mathrm {d} ^ {2}} {\ mathrm {d} \ varphi ^ {2}}} E (\ varphi, e) \ right),}$

hvor a er den semi-store akse , og e er excentriciteten .

Den ufuldstændige elliptiske integral af den anden art har følgende tilføjelsessætning:

${\ displaystyle E [\ arctan (x), k] + E [\ arctan (y), k] = E \ left [\ arctan \ left ({\ frac {x {\ sqrt {k '^ {2} y ^ {2} +1}}} {\ sqrt {y ^ {2} +1}}} \ højre) + \ arctan \ left ({\ frac {y {\ sqrt {k '^ {2} x ^ { 2} +1}}} {\ sqrt {x ^ {2} +1}}} til højre), k \ højre] + {\ frac {k ^ {2} xy} {k '^ {2} x ^ {2} y ^ {2} + x ^ {2} + y ^ {2} +1}} \ venstre ({\ frac {x {\ sqrt {k '^ {2} y ^ {2} +1} }} {\ sqrt {y ^ {2} +1}}} + {\ frac {y {\ sqrt {k '^ {2} x ^ {2} +1}}} {\ sqrt {x ^ {2 } +1}}} \ højre)}$

Den elliptiske modul kan transformeres på den måde:

${\ displaystyle E [\ arcsin (x), k] = (1 + {\ sqrt {1-k ^ {2}}}) E \ left [\ arcsin \ left [{\ frac {(1 + {\ sqrt {1-k ^ {2}}}) x} {1 + {\ sqrt {1-k ^ {2} x ^ {2}}}} \ højre], {\ frac {1 - {\ sqrt { 1-k ^ {2}}}} {1 + {\ sqrt {1-k ^ {2}}}} \ højre] - {\ sqrt {1-k ^ {2}}} F [\ arcsin ( x), k] + {\ frac {k ^ {2} x {\ sqrt {1-x ^ {2}}}} {1 + {\ sqrt {1-k ^ {2} x ^ {2}} }}}}$

Ufuldstændig elliptisk integral af den tredje art

Den ufuldstændige elliptiske integral af den tredje art Π er

${\ displaystyle \ Pi (n; \ varphi \ setminus \ alpha) = \ int _ {0} ^ {\ varphi} {\ frac {1} {1-n \ sin ^ {2} \ theta}} {\ frac {\ mathrm {d} \ theta} {\ sqrt {1- \ left (\ sin \ theta \ sin \ alpha \ right) ^ {2}}}}$

eller

${\ displaystyle \ Pi (n; \ varphi \, | \, m) = \ int _ {0} ^ {\ sin \ varphi} {\ frac {1} {1-nt ^ {2}}} {\ frac {\ mathrm {d} t} {\ sqrt {\ left (1-mt ^ {2} \ right) \ left (1-t ^ {2} \ right)}}.}$

Nummeret n kaldes karakteristikken og kan få en hvilken som helst værdi uafhængigt af de andre argumenter. Bemærk dog, at værdien Π (1; π/2| m ) er uendelig, for enhver m .

Et forhold til de Jacobianske elliptiske funktioner er

${\ displaystyle \ Pi {\ bigl (} n; \, \ operatorname {am} (u; k); \, k {\ bigr)} = \ int _ {0} ^ {u} {\ frac {\ mathrm {d} w} {1-n \, \ operatorname {sn} ^ {2} (w; k)}}.}$

Meridianbuelængden fra ækvator til breddegrad φ er også relateret til et specielt tilfælde af Π :

${\ displaystyle m (\ varphi) = a \ left (1-e ^ {2} \ right) \ Pi \ left (e ^ {2}; \ varphi \, | \, e ^ {2} \ right). }$

Komplet elliptisk integral af den første slags

Elliptiske integraler siges at være 'komplette', når amplituden φ =π/2og derfor x = 1 . Den komplette elliptiske integral af den første slags K kan således defineres som

${\ displaystyle K (k) = \ int _ {0} ^ {\ tfrac {\ pi} {2}} {\ frac {\ mathrm {d} \ theta} {\ sqrt {1-k ^ {2} \ sin ^ {2} \ theta}}} = \ int _ {0} ^ {1} {\ frac {\ mathrm {d} t} {\ sqrt {\ left (1-t ^ {2} \ right) \ venstre (1-k ^ {2} t ^ {2} \ højre)}}},}$

eller mere kompakt med hensyn til den ufuldstændige integral af den første slags som

${\ displaystyle K (k) = F \ left ({\ tfrac {\ pi} {2}}, k \ right) = F \ left ({\ tfrac {\ pi} {2}} \, | \, k ^ {2} \ højre) = F (1; k).}$

Det kan udtrykkes som en magtserie

${\ displaystyle K (k) = {\ frac {\ pi} {2}} \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n)!} {2 ^ {2n} (n!) ^ {2}}} højre) ^ {2} k ^ {2n} = {\ frac {\ pi} {2}} \ sum _ {n = 0} ^ {\ infty} {\ bigl (} P_ {2n} (0) {\ bigr)} ^ {2} k ^ {2n},}$

hvor P _n er Legendre polynomier , hvilket svarer til

${\ displaystyle K (k) = {\ frac {\ pi} {2}} \ left (1+ \ left ({\ frac {1} {2}} \ right) ^ {2} k ^ {2} + \ left ({\ frac {1 \ cdot 3} {2 \ cdot 4}} \ right) ^ {2} k ^ {4} + \ cdots + \ left ({\ frac {\ left (2n-1 \ right) ) !!} {\ left (2n \ right) !!}} \ right) ^ {2} k ^ {2n} + \ cdots \ right),}$

hvor n !! betegner den dobbelte faktor . Med hensyn til Gauss hypergeometriske funktion kan den komplette elliptiske integral af den første slags udtrykkes som

${\ displaystyle K (k) = {\ tfrac {\ pi} {2}} \, {} _ {2} F_ {1} \ left ({\ tfrac {1} {2}}, {\ tfrac {1 } {2}}; 1; k ^ {2} \ højre).}$

Den komplette elliptiske integral af den første slags kaldes undertiden kvartperioden . Det kan beregnes meget effektivt i form af det aritmetiske – geometriske gennemsnit :

${\ displaystyle K (k) = {\ frac {\ frac {\ pi} {2}} {\ operatorname {agm} \ left (1, {\ sqrt {1-k ^ {2}}} \ right)} }.}$

Se Carlson (2010 , 19.8) for detaljer.

Derfor kan modulet transformeres på den måde:

${\ displaystyle K (k) = {\ frac {\ pi} {2 \ operatorname {agm} (1, {\ sqrt {1-k ^ {2}}})}} = {\ frac {\ pi} { 2 \ operatorname {agm} (1/2 + {\ sqrt {1-k ^ {2}}} / 2, {\ sqrt [{4}] {1-k ^ {2}}})}}}$

${\ displaystyle = {\ frac {\ pi} {(1 + {\ sqrt {1-k ^ {2}}}) \ operatorname {agm} [1,2 {\ sqrt [{4}] {1-k ^ {2}}} / (1 + {\ sqrt {1-k ^ {2}}})}}} = {\ frac {2} {1 + {\ sqrt {1-k ^ {2}}} }} K \ left ({\ frac {1 - {\ sqrt {1-k ^ {2}}}} {1 + {\ sqrt {1-k ^ {2}}}} \ right)}$

Dette udtryk er gyldigt for alle n ∈ ℕ og 0 ≤ k ≤ 1:

${\ displaystyle K (k) = n \ left [\ sum _ {a = 1} ^ {n} \ operatorname {dn} \ left [{\ frac {2a} {n}} K (k); k \ right ] \ højre] ^ {- 1} K \ venstre [k ^ {n} \ prod _ {a = 1} ^ {n} \ operatornavn {sn} \ venstre [{\ frac {2a-1} {n}} K (k); k \ right] ^ {2} \ right]}$

Forhold til Jacobi theta-funktion

Forholdet til Jacobis theta-funktion er givet af

${\ displaystyle K (k) = {\ frac {\ pi} {2}} \ theta _ {3} ^ {2} (q),}$

hvor nomenet q er

${\ displaystyle q (k) = \ exp \ left (- \ pi {\ frac {K \ left ({\ sqrt {1-k ^ {2}}} \ right)} {K (k)}} \ right ).}$

Asymptotiske udtryk

${\ displaystyle K \ left (k \ right) \ approx {\ frac {\ pi} {2}} + {\ frac {\ pi} {8}} {\ frac {k ^ {2}} {1-k ^ {2}}} - {\ frac {\ pi} {16}} {\ frac {k ^ {4}} {1-k ^ {2}}}}$

Denne tilnærmelse har en relativ præcision, der er bedre end 3 × 10 ⁻⁴ for k <1/2. At kun holde de to første termer er korrekt til 0,01 præcision for k <1/2.

Differentialligning

Differentialligningen for den elliptiske integral af den første slags er

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} k}} \ left (k \ left (1-k ^ {2} \ right) {\ frac {\ mathrm {d} K ( k)} {\ mathrm {d} k}} \ højre) = kK (k)}$

En anden løsning på denne ligning er . Denne løsning opfylder forholdet ${\ displaystyle K \ left ({\ sqrt {1-k ^ {2}}} \ right)}$

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} k}} K (k) = {\ frac {E (k)} {k \ left (1-k ^ {2} \ right )}} - {\ frac {K (k)} {k}}.}$

Fortsat brøkdel

En fortsat brøkudvidelse er:

${\ displaystyle {\ frac {K (k)} {2 \ pi}} = - {\ frac {1} {4}} + \ sum _ {n = 0} ^ {\ infty} {\ frac {q ^ {n}} {1 + q ^ {2n}}} = - {\ frac {1} {4}} + {\ frac {1} {1-q +}} {\ frac {(1-q) ^ { 2}} {1-q ^ {3} +}} {\ frac {q (1-q ^ {2}) ^ {2}} {1-q ^ {5} +}} {\ frac {q ^ {2} (1-q ^ {3}) ^ {2}} {1-q ^ {7} +}} {\ frac {q ^ {3} (1-q ^ {4}) ^ {2} } {1-q ^ {9} +}} \ ldots,}$

hvor nomenet er q = q ( k ) .

Komplet elliptisk integral af anden slags

Den komplette elliptiske integral af den anden type E defineres som

${\ displaystyle E (k) = \ int _ {0} ^ {\ tfrac {\ pi} {2}} {\ sqrt {1-k ^ {2} \ sin ^ {2} \ theta}} \, \ mathrm {d} \ theta = \ int _ {0} ^ {1} {\ frac {\ sqrt {1-k ^ {2} t ^ {2}}} {\ sqrt {1-t ^ {2}} }} \, \ mathrm {d} t,}$

eller mere kompakt med hensyn til den ufuldstændige integral af den anden slags E ( φ , k ) som

${\ displaystyle E (k) = E \ left ({\ tfrac {\ pi} {2}}, k \ right) = E (1; k).}$

For en ellipse med halv-hovedakse a og halv-mindre akse b og excentricitet e = √ 1 - b ² / a ² er den komplette elliptiske integral af den anden slags E ( e ) lig med en fjerdedel af omkredsen c af ellipsen målt i enheder af halv-hovedaksen a . Med andre ord:

${\ displaystyle c = 4aE (e).}$

Den komplette elliptiske integral af den anden art kan udtrykkes som en magtserie

${\ displaystyle E (k) = {\ frac {\ pi} {2}} \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n)!} {2 ^ {2n} \ left (n! \ right) ^ {2}}} \ right) ^ {2} {\ frac {k ^ {2n}} {1-2n}},}$

hvilket svarer til

${\ displaystyle E (k) = {\ frac {\ pi} {2}} \ left (1- \ left ({\ frac {1} {2}} \ right) ^ {2} {\ frac {k ^ {2}} {1}} - \ left ({\ frac {1 \ cdot 3} {2 \ cdot 4}} \ right) ^ {2} {\ frac {k ^ {4}} {3}} - \ cdots - \ left ({\ frac {(2n-1) !!} {(2n) !!}} \ right) ^ {2} {\ frac {k ^ {2n}} {2n-1}} - \ cdots \ højre).}$

Med hensyn til Gauss hypergeometriske funktion kan den komplette elliptiske integral af den anden art udtrykkes som

${\ displaystyle E (k) = {\ tfrac {\ pi} {2}} \, {} _ {2} F_ {1} \ left ({\ tfrac {1} {2}}, - {\ tfrac { 1} {2}}; 1; k ^ {2} \ højre).}$

Modulet kan transformeres på den måde:

${\ displaystyle E (k) = (1 + {\ sqrt {1-k ^ {2}}}) E \ left ({\ frac {1 - {\ sqrt {1-k ^ {2}}}} { 1 + {\ sqrt {1-k ^ {2}}}} \ højre) - {\ sqrt {1-k ^ {2}}} K (k)}$

Beregning

Ligesom integralen af ​​den første slags kan den komplette elliptiske integral af den anden art beregnes meget effektivt ved hjælp af det aritmetisk-geometriske gennemsnit ( Carlson 2010 , 19.8).

Definer sekvenser, og hvor , og gentagelsesforholdene , hold. Desuden definer . Per definition, ${\ displaystyle a_ {n}}$${\ displaystyle g_ {n}}$${\ displaystyle a_ {0} = 1}$${\ displaystyle g_ {0} = {\ sqrt {1-k ^ {2}}} = k '}$${\ displaystyle a_ {n + 1} = {\ frac {a_ {n} + g_ {n}} {2}}}$${\ displaystyle g_ {n + 1} = {\ sqrt {a_ {n} g_ {n}}}}$${\ displaystyle c_ {n} = {\ sqrt {\ left | a_ {n} ^ {2} -g_ {n} ^ {2} \ right |}}}$

${\ displaystyle a _ {\ infty} = \ lim _ {n \ to \ infty} a_ {n} = \ lim _ {n \ to \ infty} g_ {n} = \ operatorname {agm} (1, {\ sqrt {1-k ^ {2}}})}$.

Også . Derefter ${\ displaystyle \ lim _ {n \ to \ infty} c_ {n} = 0}$

${\ displaystyle E (k) = {\ frac {\ pi} {2a _ {\ infty}}} \ left (1- \ sum _ {n = 0} ^ {\ infty} 2 ^ {n-1} c_ { n} ^ {2} \ højre).}$

I praksis ville det aritmetisk-geometriske gennemsnit simpelthen blive beregnet op til en vis grænse. Denne formel konvergerer kvadratisk for alle . For at fremskynde beregningen yderligere kan forholdet bruges. ${\ displaystyle | k | \ leq 1}$${\ displaystyle c_ {n + 1} = {\ frac {c_ {n} ^ {2}} {4a_ {n + 1}}}}$

Derivat og differentialligning

${\ displaystyle {\ frac {\ mathrm {d} E (k)} {\ mathrm {d} k}} = {\ frac {E (k) -K (k)} {k}}}$

${\ displaystyle \ left (k ^ {2} -1 \ right) {\ frac {\ mathrm {d}} {\ mathrm {d} k}} \ left (k \; {\ frac {\ mathrm {d} E (k)} {\ mathrm {d} k}} \ højre) = kE (k)}$

En anden løsning på denne ligning er E ( √ 1 - k ² ) - K ( √ 1 - k ² ) .

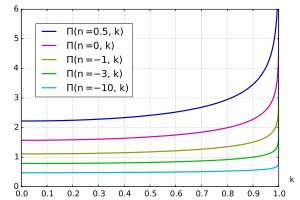
Komplet elliptisk integral af den tredje art

Den komplette elliptiske integral af den tredje art Π kan defineres som

${\ displaystyle \ Pi (n, k) = \ int _ {0} ^ {\ tfrac {\ pi} {2}} {\ frac {\ mathrm {d} \ theta} {\ left (1-n \ sin ^ {2} \ theta \ right) {\ sqrt {1-k ^ {2} \ sin ^ {2} \ theta}}}.}$

Bemærk, at den elliptiske integral af den tredje art undertiden defineres med et omvendt tegn for karakteristikken n ,

${\ displaystyle \ Pi '(n, k) = \ int _ {0} ^ {\ tfrac {\ pi} {2}} {\ frac {\ mathrm {d} \ theta} {\ left (1 + n \ sin ^ {2} \ theta \ right) {\ sqrt {1-k ^ {2} \ sin ^ {2} \ theta}}}.}$

Ligesom de komplette elliptiske integraler af den første og anden slags kan den komplette elliptiske integral af den tredje art beregnes meget effektivt ved hjælp af det aritmetisk-geometriske gennemsnit ( Carlson 2010 , 19.8).

Delvise derivater

${\ displaystyle {\ begin {align} {\ frac {\ partial \ Pi (n, k)} {\ partial n}} & = {\ frac {1} {2 \ left (k ^ {2} -n \ højre) (n-1)}} \ venstre (E (k) + {\ frac {1} {n}} \ venstre (k ^ {2} -n \ højre) K (k) + {\ frac {1 } {n}} \ left (n ^ {2} -k ^ {2} \ right) \ Pi (n, k) \ right) \\ [10px] {\ frac {\ partial \ Pi (n, k) } {\ partial k}} & = {\ frac {k} {nk ^ {2}}} \ left ({\ frac {E (k)} {k ^ {2} -1}} + \ Pi (n , k) \ højre) \ slut {justeret}}}$

Funktionelle relationer

Legendres forhold :

${\ displaystyle K (k) E \ left ({\ sqrt {1-k ^ {2}}} \ right) + E (k) K \ left ({\ sqrt {1-k ^ {2}}} \ højre) -K (k) K \ venstre ({\ sqrt {1-k ^ {2}}} \ højre) = {\ frac {\ pi} {2}}.}$

Se også

Referencer

• Abramowitz, Milton ; Stegun, Irene Ann , red. (1983) [juni 1964]. "Kapitel 17" . Håndbog med matematiske funktioner med formler, grafer og matematiske tabeller . Anvendt matematik-serie. 55 (Niende genoptryk med yderligere korrektioner af tiende originaltryk med rettelser (december 1972); første udgave). Washington DC; New York: US Department of Commerce, National Bureau of Standards; Dover-publikationer. s. 587. ISBN 978-0-486-61272-0. LCCN  64-60036 . MR  0167642 . LCCN  65-12253 .
• Byrd, PF; Friedman, MD (1971). Handbook of Elliptic Integrals for Engineers and Scientists (2. udgave). New York: Springer-Verlag. ISBN 0-387-05318-2.
• Carlson, BC (1995). "Numerisk beregning af reelle eller komplekse elliptiske integraler". Numeriske algoritmer . 10 (1): 13–26. arXiv : matematik / 9409227 . Bibcode : 1995NuAlg..10 ... 13C . doi : 10.1007 / BF02198293 .
• Carlson, BC (2010), "Elliptic integral" , i Olver, Frank WJ ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (red.), NIST-håndbog om matematiske funktioner , Cambridge University Press, ISBN 978-0-521-19225-5, MR  2723248
• Erdélyi, Arthur; Magnus, Wilhelm ; Oberhettinger, Fritz; Tricomi, Francesco G. (1953). Højere transcendentale funktioner. Bind II (PDF) . McGraw-Hill Book Company, Inc., New York-Toronto-London. MR  0058756 .
• Gradshteyn, Izrail Solomonovich ; Ryzhik, Iosif Moiseevich ; Geronimus, Yuri Veniaminovich ; Tseytlin, Michail Yulyevich ; Jeffrey, Alan (2015) [oktober 2014]. "8.1.". I Zwillinger, Daniel; Moll, Victor Hugo (red.). Tabel over integraler, serier og produkter . Oversat af Scripta Technica, Inc. (8. udgave). Academic Press, Inc. ISBN 978-0-12-384933-5. LCCN  2014010276 .
• Greenhill, Alfred George (1892). Anvendelsen af ​​elliptiske funktioner . New York: Macmillan.
• Hancock, Harris (1910). Forelæsninger om teorien om elliptiske funktioner . New York: J. Wiley & sons.
• King, Louis V. (1924). Om den direkte numeriske beregning af elliptiske funktioner og integraler . Cambridge University Press.
• Tryk på, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Afsnit 6.12. Elliptiske integraler og Jacobian elliptiske funktioner" , Numeriske opskrifter: The Art of Scientific Computing (3. udgave), New York: Cambridge University Press, ISBN 978-0-521-88068-8

eksterne links

• "Elliptisk integral" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Eric W. Weisstein, "Elliptic Integral" (Mathworld)
• Matlab-kode til evaluering af elliptiske integraler efter elliptisk projekt
• Rationelle tilnærmelser til komplette elliptiske integraler (Exstrom Laboratories)
• En kort historie om elliptiske integrationssætninger