Klassificering af diskontinuiteter - Classification of discontinuities

Kontinuerlige funktioner er af største betydning i matematik , funktioner og applikationer. Men ikke alle funktioner er kontinuert . Hvis en funktion ikke er kontinuerlig på et tidspunkt i sit domæne , siger man, at den har en diskontinuitet der. Det sæt af alle punkter af diskontinuitet af en funktion kan være et diskret sæt , et tæt sæt , eller endda hele domænet af funktionen. Denne artikel beskriver klassificeringen af ​​diskontinuiteter i det enkleste tilfælde af funktioner i en enkelt reel variabel, der tager reelle værdier.

Den svingning af en funktion i et punkt kvantificerer disse diskontinuiteter som følger:

• i en aftagelig diskontinuitet er afstanden, som værdien af ​​funktionen er slukket for, oscillationen ;
• i en springdiskontinuitet er springets størrelse svingningen (forudsat at værdien ved punktet ligger mellem disse grænser for de to sider);
• i en væsentlig diskontinuitet måler oscillation, at en grænse ikke eksisterer ; grænsen er konstant.

Et specielt tilfælde er, hvis funktionen afviger til uendelig eller minus uendelig , i hvilket tilfælde svingningen ikke er defineret (i de udvidede reelle tal er dette en aftagelig diskontinuitet).

Klassifikation

For hvert af følgende skal du overveje en reel værdsat funktion f af en reel variabel x , defineret i et område ved det punkt x _0, hvor f er diskontinuerligt.

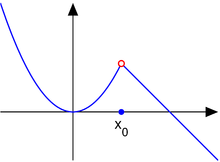
Aftagelig diskontinuitet

Overvej den stykkevis funktion

${\ displaystyle f (x) = {\ begin {cases} x^{2} & {\ mbox {for}} x <1 \\ 0 & {\ mbox {for}} x = 1 \\ 2-x & {\ mbox {for}} x> 1 \ end {cases}}}$

Punktet x ₀ = 1 er en aftagelig diskontinuitet . For denne form for diskontinuitet:

Den ensidige grænse fra den negative retning:

${\ displaystyle L^{-} = \ lim _ {x \ til x_ {0}^{-}} f (x)}$

og den ensidige grænse fra den positive retning:

${\ displaystyle L^{+} = \ lim _ {x \ til x_ {0}^{+}} f (x)}$

ved x ₀ eksisterer begge , er begrænsede og er lig med L = L ^- = L ⁺ . Med andre ord, da de to ensidige grænser eksisterer og er ens, eksisterer grænsen L for f ( x ), når x nærmer sig x ₀ , og er lig med den samme værdi. Hvis den faktiske værdi af f ( x ₀ ) er ikke lig med L , så x ₀ kaldes en aftagelig diskontinuitet . Denne diskontinuitet kan fjernes for at gøre f kontinuerlig ved x ₀ , eller mere præcist, funktionen

${\ displaystyle g (x) = {\ begin {cases} f (x) & x \ neq x_ {0} \\ L & x = x_ {0} \ end {cases}}}$

er kontinuerlig ved x = x ₀ .

Udtrykket flytbar diskontinuitet udvides undertiden til at omfatte en flytbar singularitet , hvor grænserne i begge retninger eksisterer og er ens, mens funktionen er udefineret ved punktet x ₀ . Denne anvendelse er et misbrug af terminologi, fordi kontinuitet og diskontinuitet af en funktion er begreber, der kun defineres for punkter i funktionens domæne.

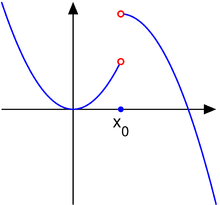
Spring diskontinuitet

Overvej funktionen

${\ displaystyle f (x) = {\ begin {cases} x^{2} & {\ mbox {for}} x <1 \\ 0 & {\ mbox {for}} x = 1 \\ 2- (x- 1)^{2} & {\ mbox {for}} x> 1 \ end {cases}}}$

Punktet x ₀ = 1 er derefter en springdiskontinuitet .

I dette tilfælde har en enkelt grænse ikke eksisterer, fordi den ensidige grænser, L ^- og L ⁺ , eksisterer og er begrænsede, men er ikke lige: siden, L ^- ≠ L ⁺ , grænsen L findes ikke. Derefter kaldes x ₀ en springdiskontinuitet , trindiskontinuitet eller diskontinuitet af den første slags . For denne type diskontinuitet kan funktionen f have en hvilken som helst værdi på x ₀ .

Væsentlig diskontinuitet

For en væsentlig diskontinuitet eksisterer mindst en af ​​de to ensidige grænser ikke. Overvej funktionen

${\ displaystyle f (x) = {\ begin {cases} \ sin {\ frac {5} {x-1}} & {\ text {for}} x <1 \\ 0 & {\ text {for}} x = 1 \\ {\ frac {1} {x-1}} og {\ tekst {for}} x> 1. \ slut {cases}}}$

Derefter er pointen en væsentlig diskontinuitet . ${\ displaystyle x_ {0} = 1}$

I dette eksempel eksisterer begge og eksisterer ikke, og opfylder dermed betingelsen om væsentlig diskontinuitet. Så x ₀ er en væsentlig diskontinuitet, uendelig diskontinuitet eller diskontinuitet af den anden slags. (Dette adskiller sig fra en væsentlig singularitet , som ofte bruges, når man studerer funktioner af komplekse variabler .) ${\ displaystyle L^{-}}$${\ displaystyle L^{+}}$

Sættet med diskontinuiteter i en funktion

Antag at f er en funktion defineret på et interval . Vi betegner med sættet alle diskontinuiteter i intervallet for funktionen f . De to følgende egenskaber ved sættet er relevante i litteraturen. ${\ displaystyle I \ delsæt \ mathbb {R}}$${\ displaystyle D}$${\ displaystyle I}$${\ displaystyle D}$

• Sættet med er et F _σ sæt . Sættet af punkter, hvor en funktion er kontinuerlig, er altid et G _δ -sæt .${\ displaystyle D}$

• Hvis på intervallet , f er monoton, kan det højst tælles . Dette er Frodas sætning .${\ displaystyle I}$${\ displaystyle D}$
• Når og f er en afgrænset funktion, er det velkendt betydningen af ​​sættet med hensyn til Riemanns integritet af f . Faktisk siger Lebesgue-Vitali sætning, at f er Riemann integrerbar på, hvis og kun hvis har nul Lebesgue-måling.${\ displaystyle I = [a, b]}$${\ displaystyle D}$${\ displaystyle I = [a, b]}$${\ displaystyle D}$

For Lebesgue-Vitali lader til, at alle typer af diskontinuiteter har samme vægt på forhindringen, at en afgrænset funktion f være Riemann integrable på . Dette er imidlertid ikke tilfældet. Faktisk har visse diskontinuiteter absolut ingen rolle for funktionens integritet i Riemann. For at præcisere dette spørgsmål er det værd at opdele sættet i de følgende tre sæt, der svarer til den type diskontinuiteter, der oprindeligt blev betragtet. ${\ displaystyle [a, b]}$${\ displaystyle D}$

Til dette formål vil vi betyde mængden af ​​alt sådan, at f har en aftagelig diskontinuitet ved . Analogt ved betegner vi det sæt, der udgøres af alt sådant, at f har en springdiskontinuitet ved . Sættet med alle sådanne, som f har en væsentlig diskontinuitet ved, vil blive betegnet med . Sættet af alle diskontinuiteter på intervallet for funktionen f er naturligvis sådan, at . ${\ displaystyle R}$${\ displaystyle x_ {0} \ i I}$${\ displaystyle x_ {0}}$${\ displaystyle J}$${\ displaystyle x_ {0} \ i I}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {0} \ i I}$${\ displaystyle x_ {0}}$${\ displaystyle E}$${\ displaystyle D}$${\ displaystyle I}$${\ displaystyle D = R \ kop J \ kop E}$

Sættet med alle væsentlige diskontinuiteter kan opdeles i følgende to sæt: ${\ displaystyle E}$

${\ displaystyle E_ {1} = \ {x_ {0} \ i E: \ lim _ {x \ til x_ {0}^{-}} f (x)}$og eksisterer ikke og enten eller eksisterer . ${\ displaystyle \ lim _ {x \ til x_ {0}^{+}} f (x)}$${\ displaystyle \}}$${\ displaystyle E_ {2} = \ {x_ {0} \ i E:}$${\ displaystyle \ lim _ {x \ til x_ {0}^{-}} f (x)}$${\ displaystyle \ lim _ {x \ til x_ {0}^{+}} f (x)}$${\ displaystyle \}}$

Selvfølgelig . Når vi vil sige, er det en væsentlig diskontinuitet af første art . For enhver vil vi kalde det en væsentlig diskontinuitet af anden slags.${\ displaystyle E = E_ {1} \ cup E_ {2}}$${\ displaystyle x_ {0} \ i E_ {1}}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {0} \ i E_ {2}}$

Man har følgende vigtige egenskab (se):

• Sættet kan tælles.${\ displaystyle R \ kop J \ kop E_ {2}}$

Derfor kan Lebesgue-Vitali-sætningen omformuleres som følger:

• En afgrænset funktion, f , er Riemann integrerbar på, hvis og kun hvis korrespondentsættet af alle væsentlige diskontinuiteter af første slags f har nul Lebesgue -måling.${\ displaystyle [a, b]}$${\ displaystyle E_ {1}}$

Thomaes funktion er diskontinuerlig på alle ikke-nul rationelle punkter , men kontinuerlig på alle irrationelle punkter. Man ser let, at disse diskontinuiteter alle er væsentlige af den første slags. Ved første afsnit eksisterer der ikke en funktion, der er kontinuerlig på hvert rationelt punkt, men diskontinuerligt på hvert irrationelt punkt.

Den indikatorfunktion af rationals, også kendt som Dirichlet funktion , er diskontinuerlig overalt . Disse diskontinuiteter er også alle væsentlige af den første slags.

Eksempel

Overvej nu Cantor -sættet og dets indikator (eller karakteristiske) funktion${\ displaystyle {\ mathcal {C}} \ undersæt [0,1]}$

I betragtning af diskontinuiteterne i denne funktion, lad os antage et punkt . Derfor findes der et sæt , der bruges i formuleringen af , som ikke indeholder . Det vil sige tilhører et af de åbne intervaller, som blev fjernet i konstruktionen af . På denne måde har et kvarter uden punkter , hvor der som følge heraf kun antages værdien nul. Derfor er kontinuerlig i . Dette betyder, at sættet af alle diskontinuiteter af intervallet er en delmængde af . Da er et ikke-tælleligt sæt med nul Lebesgue-måling, er det også et nul-Lebesgue- målesæt, og så med hensyn til Lebesgue-Vitali-sætningen er en Riemann-integrerbar funktion. ${\ displaystyle x_ {0} \ not \ in {\ mathcal {C}}}$${\ displaystyle C_ {n}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {0}}$${\ displaystyle C_ {n}}$${\ displaystyle x_ {0}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}} (x)}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}}}$${\ displaystyle x_ {0}}$${\ displaystyle D}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}}}$${\ displaystyle [0,1]}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle D}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}}}$

Men mere præcist har man . Faktisk hvis der ikke kan indeholde nogen nabohoof af . Ellers skal vi have, for hver , som er absurd. da hvert af disse sæt er sammensat af interval med længde , hvilket ikke tillader denne inklusion for værdier af tilstrækkeligt store på den måde . På denne måde indeholder ethvert kvarter af punkter og punkter, der ikke er af . Med hensyn til funktionen betyder det, at både og ikke findes. Det vil sige, hvor vi som før betegner sættet med alle væsentlige diskontinuiteter af den første slags funktion . Klart${\ displaystyle D = {\ mathcal {C}}}$${\ displaystyle x_ {0} \ i {\ mathcal {C}}}$${\ displaystyle {\ bigl (} x_ {0}-\ epsilon, x_ {0}+\ epsilon {\ bigr)}}$${\ displaystyle x_ {0}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle n}$${\ displaystyle {\ bigl (} x_ {0}-\ epsilon, x_ {0}+\ epsilon {\ bigr)} \ undersæt C_ {n}}$${\ displaystyle 3^{-n}}$${\ displaystyle n}$${\ displaystyle 3^{-n} <\ epsilon}$${\ displaystyle x_ {0} \ i {\ mathcal {C}}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}}}$${\ displaystyle \ lim _ {x \ til x_ {0}^{-}} \ mathbf {1} _ {\ mathcal {C}} (x)}$${\ displaystyle \ lim _ {x \ til x_ {0}^{+}} 1 _ {\ mathcal {C}} (x)}$${\ displaystyle D = E_ {1}}$${\ displaystyle E_ {1}}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}}}$${\ displaystyle \ int _ {0}^{1} \ mathbf {1} _ {\ mathcal {C}} (x) dx = 0.}$

Se også

• Aftagelig singularitet
• Matematisk singularitet
• Forlængelse ved kontinuitet
• Glathed
  • Geometrisk kontinuitet
  • Parametrisk kontinuitet

Noter

Referencer

Kilder

• Malik, SC; Arora, Savita (1992). Matematisk analyse (2. udgave). New York: Wiley. ISBN 0-470-21858-4.

eksterne links

• "Diskontinuerlig" . PlanetMath .
• "Diskontinuitet" af Ed Pegg, Jr. , The Wolfram Demonstrations Project , 2007.
• Weisstein, Eric W. "Diskontinuitet" . MathWorld .
• Kudryavtsev, LD (2001) [1994], "Discontinuity point" , Encyclopedia of Mathematics , EMS Press