Markov kæde - Markov chain

Del af en serie om statistik
Sandsynlighedsteori
Sandsynlighed Aksiomer Determinisme System Ubestemmelse Tilfældighed
Sandsynlighedsrum Prøveplads Begivenhed Kollektivt udtømmende begivenheder Elementær begivenhed Gensidig eksklusivitet Resultat Singleton Eksperiment Bernoulli -retssag Sandsynlighedsfordeling Bernoulli distribution Binomial fordeling Normal fordeling Sandsynlighedsmåling Tilfældig variabel Bernoulli -proces Kontinuerlig eller diskret Forventet værdi Markov kæde Observeret værdi Tilfældig gåtur Stokastisk proces
Supplerende begivenhed Fælles sandsynlighed Marginal sandsynlighed Betinget sandsynlighed
Uafhængighed Betinget uafhængighed Lov om total sandsynlighed Lov om store tal Bayes 'sætning Booles ulighed
Venn diagram Trædiagram
v t e

Et diagram, der repræsenterer en to-tilstands Markov-proces, med tilstande mærket E og A. Hvert nummer repræsenterer sandsynligheden for, at Markov-processen ændres fra en tilstand til en anden tilstand, med retningen angivet med pilen. For eksempel, hvis Markov -processen er i tilstand A, er sandsynligheden, den ændrer til tilstand E, 0,4, mens sandsynligheden for, at den forbliver i tilstand A, er 0,6.

En Markov -kæde eller Markov -proces er en stokastisk model, der beskriver en række mulige begivenheder, hvor sandsynligheden for hver begivenhed kun afhænger af den tilstand, der var opnået i den foregående begivenhed. En utallig uendelig sekvens, hvor kæden bevæger sig ved diskrete tidstrin, giver en diskret tid Markov-kæde (DTMC). En proces med kontinuerlig tid kaldes en kontinuerlig Markov-kæde (CTMC). Det er opkaldt efter den russiske matematiker Andrey Markov .

Markov-kæder har mange applikationer som statistiske modeller af virkelige processer, såsom undersøgelse af fartpilotsystemer i motorkøretøjer , køer eller køer af kunder, der ankommer til en lufthavn, valutakurser og dynamik i dyrebefolkningen.

Markov -processer er grundlaget for generelle stokastiske simuleringsmetoder kendt som Markov -kæden Monte Carlo , som bruges til at simulere prøveudtagning fra komplekse sandsynlighedsfordelinger og har fundet anvendelse i bayesisk statistik , termodynamik , statistisk mekanik , fysik , kemi , økonomi , finans , signal behandling , informationsteori og talebehandling .

Adjektiverne Markovian og Markov bruges til at beskrive noget, der er relateret til en Markov -proces.

Introduktion

Den russiske matematiker Andrey Markov

Definition

En Markov -proces er en stokastisk proces, der opfylder Markov -egenskaben (undertiden karakteriseret som " hukommelsesløshed "). I enklere termer er det en proces, for hvilken der kan forudsiges fremtidige resultater udelukkende baseret på dets nuværende tilstand, og - vigtigst af alt - sådanne forudsigelser er lige så gode som dem, der kunne gøres ved at kende processens fulde historie. Med andre ord, betinget af systemets nuværende tilstand, dets fremtidige og tidligere stater er uafhængige .

En Markov -kæde er en type Markov -proces, der enten har et diskret tilstandsrum eller et diskret indekssæt (ofte repræsenterer tid), men den præcise definition af en Markov -kæde varierer. For eksempel er det almindeligt at definere en Markov -kæde som en Markov -proces i enten diskret eller kontinuerlig tid med et tællbart tilstandsrum (altså uanset tidens art), men det er også almindeligt at definere en Markov -kæde som at have diskret tid i enten tællbart eller kontinuerligt tilstandsrum (altså uanset tilstandsrummet).

Typer af Markov -kæder

Systemets tilstandsrum og tidsparameterindeks skal specificeres. Følgende tabel giver et overblik over de forskellige forekomster af Markov -processer for forskellige niveauer af statens rumgeneralitet og for diskret tid v. Kontinuerlig tid:

Bemærk, at der ikke er endegyldig enighed i litteraturen om brugen af ​​nogle af de udtryk, der betegner særlige tilfælde af Markov -processer. Normalt er udtrykket "Markov-kæde" forbeholdt en proces med et diskret sæt af tidspunkter, det vil sige en diskret-tid Markov-kæde (DTMC) , men nogle få forfattere bruger udtrykket "Markov-proces" til at henvise til en kontinuerlig tid Markov -kæde (CTMC) uden eksplicit omtale. Derudover er der andre udvidelser af Markov -processer, der omtales som sådanne, men ikke nødvendigvis falder inden for nogen af ​​disse fire kategorier (se Markov -modellen ). Desuden behøver tidsindekset ikke nødvendigvis at være reelt værdiansat; ligesom med statsrummet, er der tænkelige processer, der bevæger sig gennem indekssæt med andre matematiske konstruktioner. Bemærk, at den generelle tilstandsrums kontinuerlige Markov-kæde er generel i en sådan grad, at den ikke har et bestemt udtryk.

Selvom tidsparameteren normalt er diskret, har tilstandsrummet i en Markov-kæde ikke nogen generelt aftalte begrænsninger: udtrykket kan referere til en proces på et vilkårligt statsrum. Imidlertid anvender mange anvendelser af Markov -kæder begrænsede eller utallige uendelige tilstandsrum, som har en mere ligetil statistisk analyse. Udover parametre for tidsindeks og tilstandsrum er der mange andre variationer, udvidelser og generaliseringer (se Variationer ). For enkelthed koncentrerer det meste af denne artikel sig om diskret-tid, diskret tilstand-rum-sag, medmindre andet er nævnt.

Overgange

Systemets tilstandsændringer kaldes overgange. Sandsynlighederne forbundet med forskellige tilstandsændringer kaldes overgangssandsynligheder. Processen er kendetegnet ved et tilstandsrum, en overgangsmatrix, der beskriver sandsynlighederne for bestemte overgange, og en indledende tilstand (eller indledende fordeling) på tværs af statsrummet. Ved konvention antager vi, at alle mulige tilstande og overgange er inkluderet i definitionen af ​​processen, så der er altid en næste tilstand, og processen afsluttes ikke.

En tilfældig proces i diskret tid involverer et system, der er i en bestemt tilstand ved hvert trin, hvor tilstanden tilfældigt ændres mellem trinene. Trinene betragtes ofte som øjeblikke i tiden, men de kan lige så godt referere til fysisk afstand eller enhver anden diskret måling. Formelt er trinene heltal eller naturlige tal , og den tilfældige proces er en kortlægning af disse til tilstande. Markov -ejendommen angiver, at den betingede sandsynlighedsfordeling for systemet i det næste trin (og faktisk ved alle fremtidige trin) kun afhænger af systemets aktuelle tilstand og ikke yderligere af systemets tilstand ved tidligere trin.

Da systemet ændres tilfældigt, er det generelt umuligt med sikkerhed at forudsige tilstanden af ​​en Markov -kæde på et givet tidspunkt i fremtiden. Imidlertid kan de statistiske egenskaber for systemets fremtid forudsiges. I mange applikationer er det disse statistiske egenskaber, der er vigtige.

Historie

Markov studerede Markov -processer i begyndelsen af ​​det 20. århundrede og udgav sit første papir om emnet i 1906. Markov -processer i kontinuerlig tid blev opdaget længe før Andrey Markovs arbejde i begyndelsen af ​​det 20. århundrede i form af Poisson -processen . Markov var interesseret i at studere en forlængelse af uafhængige tilfældige sekvenser, motiveret af en uenighed med Pavel Nekrasov, der hævdede, at uafhængighed var nødvendig for den svage lov om store tal . I sit første papir om Markov -kæder, der blev offentliggjort i 1906, viste Markov, at Markov -kædens gennemsnitlige resultater under visse omstændigheder ville konvergere til en fast vektorværdier, hvilket beviser en svag lov af store tal uden den uafhængighedsantagelse, som havde været almindeligt betragtet som et krav for sådanne matematiske love at holde. Markov brugte senere Markov -kæder til at studere fordelingen af ​​vokaler i Eugene Onegin , skrevet af Alexander Pushkin , og viste sig at være en central grænsesætning for sådanne kæder.

I 1912 studerede Henri Poincaré Markov -kæder på begrænsede grupper med det formål at studere kortblanding. Andre tidlige anvendelser af Markov -kæder inkluderer en diffusionsmodel, introduceret af Paul og Tatyana Ehrenfest i 1907, og en forgreningsproces, introduceret af Francis Galton og Henry William Watson i 1873, forud for Markovs arbejde. Efter arbejdet i Galton og Watson blev det senere afsløret, at deres forgreningsproces uafhængigt var blevet opdaget og studeret omkring tre årtier tidligere af Irénée-Jules Bienaymé . Fra 1928 blev Maurice Fréchet interesseret i Markov -kæder, hvilket til sidst resulterede i, at han i 1938 udgav en detaljeret undersøgelse af Markov -kæder.

Andrei Kolmogorov udviklede i et papir fra 1931 en stor del af den tidlige teori om kontinuerlige Markov-processer. Kolmogorov var delvist inspireret af Louis Bacheliers 1900 -arbejde med udsving på aktiemarkedet samt Norbert Wieners arbejde med Einsteins model for brunisk bevægelse. Han introducerede og studerede et bestemt sæt Markov -processer kendt som diffusionsprocesser, hvor han udledte et sæt differentialligninger, der beskriver processerne. Uafhængigt af Kolmogorovs arbejde frembragte Sydney Chapman i et papir fra 1928 en ligning, nu kaldet Chapman – Kolmogorov -ligningen , på en mindre matematisk streng måde end Kolmogorov, mens han studerede Brownsk bevægelse. Differentialligningerne kaldes nu Kolmogorov -ligningerne eller Kolmogorov – Chapman -ligningerne. Andre matematikere, der bidrog væsentligt til grundlaget for Markov -processer, omfatter William Feller , der begyndte i 1930'erne og derefter senere Eugene Dynkin , der startede i 1950'erne.

Eksempler

Tilfældige gåture baseret på heltal og gamblerens ruinproblem er eksempler på Markov -processer. Nogle variationer af disse processer blev undersøgt hundredvis af år tidligere i forbindelse med uafhængige variabler. To vigtige eksempler på Markov -processer er Wiener -processen , også kendt som den browniske bevægelsesproces , og Poisson -processen , der betragtes som de vigtigste og centrale stokastiske processer i teorien om stokastiske processer. Disse to processer er Markov -processer i kontinuerlig tid, mens tilfældige gange på heltalene og gamblerens ruinproblem er eksempler på Markov -processer i diskret tid.

En berømt Markovkæde er den såkaldte "Drankerens walk", en random walk på antallet linje , hvor der ved hvert trin, kan positionen ændres med +1 eller -1 med lige stor sandsynlighed. Fra enhver position er der to mulige overgange, til det næste eller forrige heltal. Overgangssandsynlighederne afhænger kun af den aktuelle position, ikke af den måde, hvorpå stillingen blev nået. For eksempel er overgangssandsynlighederne fra 5 til 4 og 5 til 6 begge 0,5, og alle andre overgangssandsynligheder fra 5 er 0. Disse sandsynligheder er uafhængige af, om systemet tidligere var i 4 eller 6.

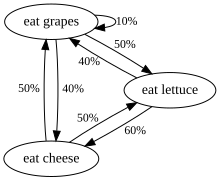
Et andet eksempel er kostvaner for et væsen, der kun spiser druer, ost eller salat, og hvis kostvaner er i overensstemmelse med følgende regler:

• Den spiser nøjagtigt en gang om dagen.
• Hvis den spiste ost i dag, spiser den i morgen salat eller druer med lige stor sandsynlighed.
• Hvis den spiste druer i dag, vil den i morgen spise druer med sandsynlighed 1/10, ost med sandsynlighed 4/10 og salat med sandsynlighed 5/10.
• Hvis den spiste salat i dag, spiser den i morgen druer med sandsynlighed 4/10 eller ost med sandsynlighed 6/10. Den spiser ikke salat igen i morgen.

Denne skabnings spisevaner kan modelleres med en Markov -kæde, da dens valg i morgen udelukkende afhænger af, hvad den spiste i dag, ikke hvad den spiste i går eller nogen anden tid tidligere. En statistisk egenskab, der kan beregnes, er den forventede procentdel over en lang periode af de dage, hvor væsenet vil spise druer.

En række uafhængige begivenheder (f.eks. En række møntvendinger) opfylder den formelle definition af en Markov -kæde. Teorien anvendes imidlertid normalt kun, når sandsynlighedsfordelingen for det næste trin ikke-trivielt afhænger af den aktuelle tilstand.

Et eksempel uden for Markov

Antag, at der er en møntpung, der indeholder fem fjerdedele (hver 25 ¢ værd), fem dimes (hver 10 ¢ værd) og fem nikkler (hver 5 ¢ værd), og en efter en trækkes mønter tilfældigt fra pungen og er dækket på et bord. Hvis repræsenterer den samlede værdi af mønterne, der er på bordet efter n trækker, med , så sekvensen er ikke en Markov proces. ${\ displaystyle X_ {n}}$${\ displaystyle X_ {0} = 0}$${\ displaystyle \ {X_ {n}: n \ i \ mathbb {N} \}}$

For at se, hvorfor dette er tilfældet, antages det, at i de første seks trækninger trækkes alle fem nikkler og en fjerdedel. Således . Hvis vi ikke bare ved , men også de tidligere værdier, så kan vi bestemme, hvilke mønter der er trukket, og vi ved, at den næste mønt ikke vil være en nikkel; så vi kan bestemme det med sandsynlighed 1. Men hvis vi ikke kender de tidligere værdier, kan vi kun baseret på værdien gætte på, at vi havde tegnet fire dimes og to nikkler, i så fald ville det helt sikkert være muligt at tegne et andet nikkel Næste. Således påvirkes vores gæt om vores viden om værdier før . ${\ displaystyle X_ {6} = \ $ 0.50}$${\ displaystyle X_ {6}}$${\ displaystyle X_ {7} \ geq \ $ 0.60}$${\ displaystyle X_ {6}}$${\ displaystyle X_ {7}}$${\ displaystyle X_ {6}}$

Det er imidlertid muligt at modellere dette scenario som en Markov -proces. I stedet for at definere at repræsentere den samlede værdi af mønterne på bordet, kunne vi definere at repræsentere antallet af de forskellige mønttyper på bordet. For eksempel kan defineres til at repræsentere staten, hvor der er en fjerdedel, nul dimes og fem nikkler på bordet efter 6 uafgjorte uafgjorte. Denne nye model ville være repræsenteret af 216 mulige stater (det vil sige 6x6x6 stater, da hver af de tre mønttyper kunne have nul til fem mønter på bordet ved afslutningen af ​​de 6 trækninger). Antag, at den første lodtrækning resulterer i tilstand . Sandsynligheden for at nå nu afhænger af ; for eksempel er staten ikke mulig. Efter den anden lodtrækning afhænger den tredje lodtrækning af, hvilke mønter der hidtil er blevet trukket, men ikke længere kun af de mønter, der blev trukket til den første stat (da sandsynligt vigtige oplysninger siden er blevet tilføjet scenariet). På denne måde afhænger statens sandsynlighed udelukkende af statens resultat . ${\ displaystyle X_ {n}}$${\ displaystyle X_ {n}}$${\ displaystyle X_ {6} = 1,0,5}$${\ displaystyle X_ {1} = 0,1,0}$${\ displaystyle X_ {2}}$${\ displaystyle X_ {1}}$${\ displaystyle X_ {2} = 1,0,1}$${\ displaystyle X_ {n} = i, j, k}$${\ displaystyle X_ {n-1} = \ ell, m, p}$

Formel definition

Diskret tid Markov kæde

En diskret tid Markov-kæde er en sekvens af tilfældige variabler X ₁ , X ₂ , X ₃ , ... med egenskaben Markov , nemlig at sandsynligheden for at flytte til den næste tilstand kun afhænger af den nuværende tilstand og ikke af den foregående tilstand hedder det:

${\ displaystyle \ Pr (X_ {n+1} = x \ midt X_ {1} = x_ {1}, X_ {2} = x_ {2}, \ ldots, X_ {n} = x_ {n}) = \ Pr (X_ {n+1} = x \ midt X_ {n} = x_ {n}),}$hvis begge betingede sandsynligheder er veldefinerede, det vil sige hvis${\ displaystyle \ Pr (X_ {1} = x_ {1}, \ ldots, X_ {n} = x_ {n})> 0.}$

De mulige værdier for X _i danner et tælleligt sæt S kaldet kædenes tilstandsrum.

Variationer

• Tidshomogene Markov-kæder er processer, hvor
  $${\ displaystyle \ Pr (X_ {n+1} = x \ mid X_ {n} = y) = \ Pr (X_ {n} = x \ mid X_ {n-1} = y)}$$

  
  for alle n . Sandsynligheden for overgangen er uafhængig af n .
• Stationære Markov -kæder er processer, hvor
  $${\ displaystyle \ Pr (X_ {0} = x_ {0}, X_ {1} = x_ {1}, \ ldots, X_ {k} = x_ {k}) = \ Pr (X_ {n} = x_ { 0}, X_ {n+1} = x_ {1}, \ ldots, X_ {n+k} = x_ {k})}$$

  
  for alle n og k . Hver stationær kæde kan bevises at være tidshomogen ved Bayes 'regel.
  En nødvendig og tilstrækkelig betingelse for, at en tidshomogen Markov-kæde er stationær, er, at fordelingen af er en stationær distribution af Markov-kæden.${\ displaystyle X_ {0}}$
• En Markov -kæde med hukommelse (eller en Markov -kæde af orden m ), hvor m er begrænset, er en tilfredsstillende proces
  $${\ displaystyle {\ begin {align} {} & \ Pr (X_ {n} = x_ {n} \ mid X_ {n-1} = x_ {n-1}, X_ {n-2} = x_ {n -2}, \ prikker, X_ {1} = x_ {1}) \\ = & \ Pr (X_ {n} = x_ {n} \ midt X_ {n-1} = x_ {n-1}, X_ {n-2} = x_ {n-2}, \ dots, X_ {nm} = x_ {nm}) {\ tekst {for}} n> m \ end {justeret}}}$$

  
  Med andre ord afhænger den fremtidige tilstand af de tidligere m -stater. Det er muligt at konstruere en kæde fra som har den klassiske Markov egenskab ved som tilstandsrum den bestilte m -tuples af X værdier, dvs. .${\ displaystyle (Y_ {n})}$${\ displaystyle (X_ {n})}$${\ displaystyle Y_ {n} = \ venstre (X_ {n}, X_ {n-1}, \ ldots, X_ {n-m+1} \ højre)}$

Kontinuerlig Markov-kæde

En kontinuerlig Markov-kæde ( X _t ) _{t  ≥ 0} er defineret af et begrænset eller tællbart tilstandsrum S , en overgangshastighedsmatrix Q med dimensioner, der er lig med tilstanden i tilstandsrummet og den indledende sandsynlighedsfordeling defineret på tilstandsrummet. For i  ≠  j er elementerne q _ij ikke-negative og beskriver hastigheden af ​​procesovergange fra tilstand i til tilstand j . Elementerne q _ii vælges således, at hver række i overgangshastighedsmatricen summerer til nul, mens rækkesummen for en sandsynlighedsovergangsmatrix i en (diskret) Markov-kæde alle er lig med en.

Der er tre tilsvarende definitioner af processen.

Uendelig definition

Den kontinuerlige tid Markov -kæden er kendetegnet ved overgangshastighederne, derivaterne med hensyn til tidspunktet for overgangssandsynlighederne mellem staterne i og j.

Lad være den tilfældige variabel, der beskriver procesens tilstand på tidspunktet t , og antag, at processen er i en tilstand i på tidspunktet t . Derefter, vel vidende , er uafhængig af tidligere værdier , og som h → 0 for alle j for alle t , ${\ displaystyle X_ {t}}$${\ displaystyle X_ {t} = i}$${\ displaystyle X_ {t+h} = j}$${\ displaystyle \ left (X_ {s}: s <t \ right)}$

${\ displaystyle \ Pr (X (t+h) = j \ mid X (t) = i) = \ delta _ {ij}+q_ {ij} h+o (h)}$,

hvor er Kronecker-deltaet ved hjælp af den lille-o notation . Den kan ses som en måling af, hvor hurtigt overgangen fra i til j sker. ${\ displaystyle \ delta _ {ij}}$${\ displaystyle q_ {ij}}$

Springkæde/fastholdelsestid definition

Definere en diskret-tid Markovkæde Y _n at beskrive n th hoppe af processen og variablerne S ₁ , S ₂ , S ₃ , ... at beskrive falder gange i hver af de stater, hvor S _i følger den eksponentielle fordeling med sats parameter - q _{Y i Y i} .

Overgangssandsynlighedsdefinition

For enhver værdi n = 0, 1, 2, 3, ... og tider indekseret op til denne værdi af n : t ₀ , t ₁ , t ₂ , ... og alle tilstande registreret på disse tidspunkter i ₀ , i ₁ , i ₂ , i ₃ , ... det holder det

${\ displaystyle \ Pr (X_ {t_ {n+1}} = i_ {n+1} \ mid X_ {t_ {0}} = i_ {0}, X_ {t_ {1}} = i_ {1}, \ ldots, X_ {t_ {n}} = i_ {n}) = p_ {i_ {n} i_ {n+1}} (t_ {n+1} -t_ {n})}$

hvor p _ij er løsningen af fremadligningen (en førsteordens differentialligning )

${\ displaystyle P '(t) = P (t) Q}$

med startbetingelse P (0) er identitetsmatrixen .

Endeligt tilstandsrum

Hvis tilstandsrummet er begrænset , kan overgangssandsynlighedsfordelingen repræsenteres af en matrix , kaldet overgangsmatrixen, med ( i , j ) th element af P lig med

${\ displaystyle p_ {ij} = \ Pr (X_ {n+1} = j \ mid X_ {n} = i).}$

Da hver række af P summer til et og alle elementer er ikke-negative, er P en højre stokastisk matrix .

Stationær fordelingsrelation til egenvektorer og forenklinger

En stationær fordeling π er en (række) vektor, hvis poster er ikke-negative og sum til 1, er uændret ved driften af ​​overgangsmatrix P på den og er således defineret af

${\ displaystyle \ pi \ mathbf {P} = \ pi.}$

Ved at sammenligne denne definition med en egenvektor ser vi, at de to begreber er relaterede og det

${\ displaystyle \ pi = {\ frac {e} {\ sum _ {i} {e_ {i}}}}}$

er et normaliseret ( ) multiplum af en venstre egenvektor e af overgangsmatrixen P med en egenværdi på 1. Hvis der er mere end en enheds egenvektor, så er en vægtet sum af de tilsvarende stationære tilstande også en stationær tilstand. Men for en Markov -kæde er man normalt mere interesseret i en stationær tilstand, der er grænsen for fordelingssekvensen for en eller anden indledende distribution. ${\ textstyle \ sum _ {i} \ pi _ {i} = 1}$

Værdierne for en stationær fordeling er forbundet med P -tilstandsrummet og dets egenvektorer har deres relative proportioner bevaret. Da komponenterne i π er positive og begrænsningen for, at deres sum er enhed, kan omskrives, da vi ser, at prikproduktet af π med en vektor, hvis komponenter alle er 1, er enhed, og at π ligger på en simplex . ${\ displaystyle \ textstyle \ pi _ {i}}$${\ textstyle \ sum _ {i} 1 \ cdot \ pi _ {i} = 1}$

Tidshomogen Markov-kæde med et begrænset tilstandsrum

Hvis Markov -kæden er tidshomogen, er overgangsmatrixen P den samme efter hvert trin, så k -trinovergangssandsynligheden kan beregnes som k -th -effekten i overgangsmatrixen, P ^k .

Hvis Markov -kæden er irreducerbar og aperiodisk, er der en unik stationær fordeling π . Derudover er der i denne sag P ^k konvergerer til en rang-on matrix, hvori hver række er den stationære fordeling π :

${\ displaystyle \ lim _ {k \ to \ infty} \ mathbf {P} ^{k} = \ mathbf {1} \ pi}$

hvor 1 er kolonnevektoren med alle poster lig med 1. Dette angives ved Perron – Frobenius sætning . Hvis der på nogen måde findes, kan den stationære distribution af den pågældende Markov -kæde let bestemmes for enhver startdistribution, som det vil blive forklaret nedenfor. ${\ textstyle \ lim _ {k \ to \ infty} \ mathbf {P} ^{k}}$

For nogle stokastiske matricer P eksisterer grænsen ikke, mens den stationære fordeling gør, som vist i dette eksempel: ${\ textstyle \ lim _ {k \ to \ infty} \ mathbf {P} ^{k}}$

${\ displaystyle \ mathbf {P} = {\ begin {pmatrix} 0 & 1 \\ 1 & 0 \ end {pmatrix}} \ qquad \ mathbf {P} ^{2k} = I \ qquad \ mathbf {P} ^{2k+1 } = \ mathbf {P}}$

${\ displaystyle {\ begin {pmatrix} {\ frac {1} {2}} og {\ frac {1} {2}} \ end {pmatrix}} {\ begin {pmatrix} 0 & 1 \\ 1 & 0 \ end {pmatrix }} = {\ begin {pmatrix} {\ frac {1} {2}} og {\ frac {1} {2}} \ end {pmatrix}}}$

(Dette eksempel illustrerer en periodisk Markov -kæde.)

Fordi der er en række forskellige særlige sager at overveje, kan processen med at finde denne grænse, hvis den findes, være en lang opgave. Der er imidlertid mange teknikker, der kan hjælpe med at finde denne grænse. Lad P være en n × n matrix, og definer${\ textstyle \ mathbf {Q} = \ lim _ {k \ to \ infty} \ mathbf {P} ^{k}.}$

Det er altid rigtigt

${\ displaystyle \ mathbf {QP} = \ mathbf {Q}.}$

Ved at trække Q fra begge sider og factoring giver derefter udbytte

${\ displaystyle \ mathbf {Q} (\ mathbf {P} -\ mathbf {I} _ {n}) = \ mathbf {0} _ {n, n},}$

hvor I _n er identitetsmatrixen i størrelse n , og 0 _{n , n} er nulmatrixen af størrelse n × n . Multiplicering af stokastiske matricer giver altid en anden stokastisk matrix, så Q må være en stokastisk matrix (se definitionen ovenfor). Det er undertiden tilstrækkeligt at anvende matrixligningen ovenfor og den omstændighed, at Q er en stokastisk matrix for at løse for Q . Inklusiv det faktum, at summen af ​​hver række i P er 1, er der n+1 ligninger til bestemmelse af n ukendte, så det er beregningsmæssigt lettere, hvis man på den ene side vælger en række i Q og erstatter hver af dens elementer med en og på den anden erstatninger det tilsvarende element (den ene i samme kolonne) i vektoren 0 , og næste venstre-multiplicerer denne sidstnævnte vektor ved den inverse af transformerede tidligere matrix for at finde Q .

Her er en metode til at gøre det: Først definerer du funktionen f ( A ) for at returnere matrixen A med den højre kolonne erstattet med alle 1'erne. Hvis [ f ( P - I _n )] ⁻¹ eksisterer derefter

${\ displaystyle \ mathbf {Q} = f (\ mathbf {0} _ {n, n}) [f (\ mathbf {P} -\ mathbf {I} _ {n})]^{ -1}.}$

Forklar: Den oprindelige matrixligning svarer til et system med n × n lineære ligninger i n × n variabler. Og der er n mere lineære ligninger fra det faktum, at Q er en højre stokastisk matrix, hvis hver række summerer til 1. Så det har brug for n × n uafhængige lineære ligninger af (n × n+n) ligningerne til at løse for n × n variabler. I dette eksempel er n-ligningerne fra "Q ganget med kolonnen til højre i (P-In)" blevet erstattet af de n stokastiske.

En ting at bemærke er, at hvis P har et element P _{i , i} på sin hoveddiagonal, der er lig med 1, og den i række eller kolonne ellers er fyldt med 0'er, så forbliver den række eller kolonne uændret i alle de efterfølgende beføjelser P ^k . Derfor er den i te række eller søjle af Q vil have de 1 og de 0'er i de samme positioner som i P .

Konvergenshastighed til den stationære distribution

Som nævnt tidligere, fra ligningen (hvis findes) den stationære (eller stabil tilstand) fordeling π er en venstre egenvektor af rækken stokastisk matrix P . Forudsat at P er diagonaliserbar eller ækvivalent, at P har n lineært uafhængige egenvektorer, udarbejdes konvergenshastigheden som følger. (For ikke-diagonaliserbare, det vil sige defekte matricer , kan man starte med Jordans normale form for P og fortsætte med et lidt mere involveret sæt argumenter på en lignende måde. ${\ displaystyle {\ boldsymbol {\ pi}} = {\ boldsymbol {\ pi}} \ mathbf {P},}$

Lad U være matrixen for egenvektorer (hver normaliseret til at have en L2 -norm lig med 1), hvor hver kolonne er en venstre egenvektor af P og lad Σ være den diagonale matrix for venstre egenværdier af P , det vil sige Σ = diag ( λ ₁ , λ ₂ , λ ₃ , ..., λ _n ). Derefter ved egen sammensætning

${\ displaystyle \ mathbf {P} = \ mathbf {U \ Sigma U} ^{-1}.}$

Lad egenværdierne opregnes således, at:

${\ displaystyle 1 = | \ lambda _ {1} |> | \ lambda _ {2} | \ geq | \ lambda _ {3} | \ geq \ cdots \ geq | \ lambda _ {n} |.}$

Da P er en række stokastisk matrix, er dens største venstre egenværdi 1. Hvis der er en unik stationær fordeling, så er den største egenværdi og den tilsvarende egenvektor også unik (fordi der ikke er nogen anden π, der løser den stationære fordelingsligning ovenfor). Lad u _i være den i -te kolonne i U -matrix, det vil sige, u _i er venstre egenvektor af P svarende til λ _i . Lad også x være en længde n række vektor, der repræsenterer en gyldig sandsynlighedsfordeling; da egenvektorerne u _i span kan vi skrive ${\ displaystyle \ mathbb {R} ^{n},}$

${\ displaystyle \ mathbf {x} ^{\ mathsf {T}} = \ sum _ {i = 1} ^{n} a_ {i} \ mathbf {u} _ {i}, \ qquad a_ {i} \ i \ mathbb {R}.}$

Hvis vi gange x med P fra højre og fortsætter denne operation med resultaterne, får vi til sidst den stationære fordeling π . Med andre ord, π = u _i ← xPP ... P = xP ^k som k → ∞. Det betyder

${\ displaystyle {\ begin {align} {\ boldsymbol {\ pi}} ^{(k)} & = \ mathbf {x} \ left (\ mathbf {U \ Sigma U} ^{-1} \ right) \ venstre (\ mathbf {U \ Sigma U} ^{-1} \ right) \ cdots \ left (\ mathbf {U \ Sigma U} ^{-1} \ right) \\ & = \ mathbf {xU \ Sigma} ^{k} \ mathbf {U} ^{-1} \\ & = \ left (a_ {1} \ mathbf {u} _ {1} ^{\ mathsf {T}}+a_ {2} \ mathbf { u} _ {2}^{\ mathsf {T}} +\ cdots +a_ {n} \ mathbf {u} _ {n}^{\ mathsf {T}} \ right) \ mathbf {U \ Sigma}^ {k} \ mathbf {U}^{-1} \\ & = a_ {1} \ lambda _ {1}^{k} \ mathbf {u} _ {1}^{\ mathsf {T}}+a_ {2} \ lambda _ {2}^{k} \ mathbf {u} _ {2}^{\ mathsf {T}} +\ cdots +a_ {n} \ lambda _ {n}^{k} \ mathbf {u} _ {n}^{\ mathsf {T}} && u_ {i} \ bot u_ {j} {\ tekst {for}} i \ neq j \\ & = \ lambda _ {1}^{k} \ venstre \ {a_ {1} \ mathbf {u} _ {1}^{\ mathsf {T}}+a_ {2} \ venstre ({\ frac {\ lambda _ {2}} {\ lambda _ {1 }}} \ højre)^{k} \ mathbf {u} _ {2}^{\ mathsf {T}}+a_ {3} \ venstre ({\ frac {\ lambda _ {3}} {\ lambda _ {1}}} \ højre)^{k} \ mathbf {u} _ {3}^{\ mathsf {T}} +\ cdots +a_ {n} \ venstre ({\ frac {\ lambda _ {n} } {\ lambda _ {1}}} \ right)^{k} \ mathbf {u} _ {n}^{\ mathsf {T}} \ right \} \ end {align}}}$

Da π = u ₁ , π ^{( k )} nærmer sig π som k → ∞ med en hastighed i størrelsesordenen λ ₂ / λ ₁ eksponentielt. Dette følger fordi dermed λ ₂ / λ ₁ er den dominerende sigt. Jo mindre forholdet er, jo hurtigere er konvergensen. Tilfældig støj i tilstandsfordelingen π kan også fremskynde denne konvergens til den stationære distribution. ${\ displaystyle | \ lambda _ {2} | \ geq \ cdots \ geq | \ lambda _ {n} |,}$

Generelt statsrum

Harris kæder

Mange resultater for Markov -kæder med begrænset tilstandsrum kan generaliseres til kæder med utallige statslige rum gennem Harris -kæder .

Brugen af ​​Markov -kæder i Markov -kæden Monte Carlo -metoder dækker tilfælde, hvor processen følger et kontinuerligt tilstandsrum.

Lokalt interagerende Markov -kæder

I betragtning af en samling af Markov -kæder, hvis udvikling tager hensyn til tilstanden i andre Markov -kæder, er relateret til forestillingen om lokalt interagerende Markov -kæder . Dette svarer til situationen, når statsrummet har en (kartesisk-) produktform. Se interaktive partikelsystem og stokastiske cellulære automater (sandsynlige cellulære automater). Se f.eks. Interaktion af Markov -processer eller

Ejendomme

To tilstande kommunikerer med hinanden, hvis begge kan nås fra hinanden med en sekvens af overgange, der har positiv sandsynlighed. Dette er et ækvivalensforhold, der giver et sæt kommunikationsklasser. En klasse lukkes, hvis sandsynligheden for at forlade klassen er nul. En Markov -kæde er ureducerbar, hvis der er en kommunikerende klasse, statsrummet.

En tilstand i har periode hvis er den største fælles divisor af antallet af overgange, hvormed jeg kan nås, startende fra i . Det er: ${\ displaystyle k}$${\ displaystyle k}$

${\ displaystyle k = \ gcd \ {n> 0: \ Pr (X_ {n} = i \ mid X_ {0} = i)> 0 \}}$

En tilstand i siges at være forbigående, hvis der fra i er en sandsynlighed for nul, at kæden aldrig vender tilbage til i . Det er ellers tilbagevendende. For en tilbagevendende tilstand i er den gennemsnitlige slåtid defineret som:

${\ displaystyle M_ {i} = E [T_ {i}] = \ sum _ {n = 1}^{\ infty} n \ cdot f_ {ii}^{(n)}.}$

Stat i er positiv tilbagevendende, hvis den er begrænset og nul recurrent ellers. Periodicitet, forgængelighed, tilbagefald og positiv og nul -gentagelse er klasseegenskaber - det vil sige, at hvis en stat har ejendommen, har alle stater i sin kommunikerende klasse ejendommen. ${\ displaystyle M_ {i}}$

En tilstand i kaldes absorberende, hvis der ikke er udgående overgange fra staten.

Ergodicitet

En tilstand i siges at være ergodisk, hvis den er aperiodisk og positiv tilbagevendende. Med andre ord er en tilstand i ergodisk, hvis den er tilbagevendende, har en periode på 1 og har en begrænset gennemsnitlig gentagelsestid. Hvis alle tilstande i en ikke -reducerbar Markov -kæde er ergodiske, siges kæden at være ergodisk.

Det kan påvises, at en ubegrænselig Markov -kæde i endelig tilstand er ergodisk, hvis den har en aperiodisk tilstand. Mere generelt, en Markovkæde er ergodic hvis der er et tal N , således at enhver stat kan nås fra enhver anden stat i et vilkårligt antal trin mindre eller lig med et antal N . I tilfælde af en fuldt tilsluttet overgangsmatrix, hvor alle overgange har en ikke-nul sandsynlighed, er denne betingelse opfyldt med  N  = 1.

En Markov-kæde med mere end én tilstand og kun en udgående overgang pr. Stat er enten ikke irreducerbar eller ikke aperiodisk, og kan derfor ikke være ergodisk.

Markoviske repræsentationer

I nogle tilfælde kan tilsyneladende ikke-markoviske processer stadig have markoviske repræsentationer, konstrueret ved at udvide begrebet 'nuværende' og 'fremtidige' stater. Lad f.eks. X være en ikke-markovsk proces. Derefter definere en proces Y , således at hver tilstand af Y betegner en tids-interval på tilstande af X . Matematisk har dette formen:

${\ displaystyle Y (t) = {\ big \ {} X (s): s \ in [a (t), b (t)] \, {\ big \}}.}$

Hvis Y har den Markov egenskab, så er det en Markovian repræsentation af X .

Et eksempel på en ikke-markovisk proces med en markovisk repræsentation er en autoregressiv tidsserie af større orden.

Hitting tider

Slagtiden er den tid, der starter i et givet sæt stater, indtil kæden ankommer i en given tilstand eller et sæt stater. Fordelingen af ​​en sådan tidsperiode har en fasetypefordeling. Den enkleste sådan fordeling er den for en enkelt eksponentielt distribueret overgang.

Forventede stødtider

For en delmængde af tilstande A  ⊆  S er vektoren k ^A for hittetider (hvor element repræsenterer den forventede værdi , startende i tilstand i , at kæden kommer ind i en af ​​tilstande i sættet A ) den minimale ikke-negative løsning til ${\ displaystyle k_ {i}^{A}}$

${\ displaystyle {\ begin {justeret} k_ {i}^{A} = 0 & {\ tekst {for}} i \ i A \\-\ sum _ {j \ i S} q_ {ij} k_ {j} ^{A} = 1 og {\ tekst {for}} i \ notin A. \ end {justeret}}}$

Tidsvending

For en CTMC X _t er den tidsomvendte proces defineret til at være . Ved Kellys lemma har denne proces den samme stationære fordeling som den fremadrettede proces. ${\ displaystyle {\ hat {X}} _ {t} = X_ {Tt}}$

En kæde siges at være reversibel, hvis den omvendte proces er den samme som den fremadrettede proces. Kolmogorovs kriterium siger, at den nødvendige og tilstrækkelige betingelse for, at en proces er reversibel, er, at produktet af overgangshastigheder omkring en lukket sløjfe skal være det samme i begge retninger.

Indlejret Markov -kæde

En metode til at finde den stationære sandsynlighedsfordeling , π , for en ergodisk kontinuerlig Markov-kæde, Q , er ved først at finde sin indlejrede Markov-kæde (EMC) . Strengt taget er EMC en almindelig diskret-tid Markov-kæde, undertiden omtalt som en springproces . Hvert element i en-trins overgangssandsynlighedsmatrixen for EMC, S , er betegnet med s _ij og repræsenterer den betingede sandsynlighed for overgang fra tilstand i til tilstand j . Disse betingede sandsynligheder kan findes af

${\ displaystyle s_ {ij} = {\ begin {cases} {\ frac {q_ {ij}} {\ sum _ {k \ neq i} q_ {ik}}} & {\ text {if}} i \ neq j \\ 0 & {\ text {ellers}}. \ end {cases}}}$

Fra dette kan S skrives som

${\ displaystyle S = I- \ venstre (\ operatorname {diag} (Q) \ right)^{-1} Q}$

hvor I er identitetsmatrixen og diag ( Q ) er den diagonale matrix dannet ved at vælge hoveddiagonalet fra matrixen Q og sætte alle andre elementer til nul.

For at finde den stationære sandsynlighedsfordelingsvektor skal vi derefter finde sådan ${\ displaystyle \ varphi}$

${\ displaystyle \ varphi S = \ varphi,}$

med at være en rækkevektor, således at alle elementer i er større end 0 og = 1. Herfra kan π findes som ${\ displaystyle \ varphi}$${\ displaystyle \ varphi}$${\ displaystyle \ | \ varphi \ | _ {1}}$

${\ displaystyle \ pi = {-\ varphi (\ operatorname {diag} (Q))^{-1} \ over \ left \ | \ varphi (\ operatorname {diag} (Q))^{-1} \ right \ | _ {1}}.}$

( S kan være periodisk, selvom Q ikke er det. Når π er fundet, skal det normaliseres til en enhedsvektor .)

En anden diskret-tidsproces, der kan stamme fra en kontinuerlig Markov-kæde, er et δ-skelet-den (diskrete-tid) Markov-kæde dannet ved at observere X ( t ) med intervaller af δ tidsenheder. De tilfældige variabler X (0),  X (δ),  X (2δ), ... giver sekvensen af ​​tilstande besøgt af δ-skelettet.

Særlige typer Markov -kæder

Markov model

Markov -modeller bruges til at modellere skiftende systemer. Der er 4 hovedtyper af modeller, der generaliserer Markov -kæder afhængigt af om hver sekventiel tilstand er observerbar eller ej, og om systemet skal justeres på grundlag af observationer foretaget:

Bernoulli -ordningen

Et Bernoulli -skema er et specielt tilfælde af en Markov -kæde, hvor overgangssandsynlighedsmatricen har identiske rækker, hvilket betyder, at den næste tilstand er uafhængig af selv den nuværende tilstand (udover at være uafhængig af de tidligere stater). En Bernoulli -ordning med kun to mulige stater er kendt som en Bernoulli -proces .

Bemærk dog ved Ornstein -isomorfismens sætning , at hver aperiodisk og irreducerbar Markov -kæde er isomorf i forhold til et Bernoulli -skema; således kan man ligeledes hævde, at Markov -kæder er et "special case" af Bernoulli -ordninger. Isomorfismen kræver generelt en kompliceret omkodning. Isomorfismens sætning er endnu en smule stærkere: den siger, at enhver stationær stokastisk proces er isomorf i forhold til et Bernoulli -skema; Markov -kæden er blot et sådant eksempel.

Delskift af endelig type

Når Markov -matricen erstattes af adjacensmatrixen for en endelig graf , er det resulterende skift udtryk en topologisk Markov -kæde eller et subskift af endelig type . En Markov -matrix, der er kompatibel med adjacensmatrixen, kan derefter give et mål på underskiftet. Mange kaotiske dynamiske systemer er isomorfe for topologiske Markov -kæder; eksempler omfatter diffeomorfier af lukkede manifolder , Prouhet – Thue – Morse-systemet , Chacon-systemet , sofic-systemer , kontekstfrie systemer og blokkodningssystemer .

Ansøgninger

Forskning har rapporteret anvendelsen og anvendeligheden af ​​Markov -kæder inden for en lang række emner som fysik, kemi, biologi, medicin, musik, spilteori og sport.

Fysik

Markoviske systemer optræder meget i termodynamik og statistisk mekanik , når der bruges sandsynligheder til at repræsentere ukendte eller umodellerede detaljer om systemet, hvis det kan antages, at dynamikken er tidsinvariant, og at der ikke er behov for at overveje relevant historie, som ikke allerede er inkluderet i statsbeskrivelsen. For eksempel fungerer en termodynamisk tilstand under en sandsynlighedsfordeling, der er vanskelig eller dyr at erhverve. Derfor kan Markov Chain Monte Carlo-metoden bruges til at tegne prøver tilfældigt fra en sort boks for at tilnærme sandsynlighedsfordelingen af ​​attributter over en række objekter.

Stierne, i den integrerede sti -formulering af kvantemekanikken, er Markov -kæder.

Markov -kæder bruges i gitter -QCD -simuleringer .

Kemi

${\ displaystyle {\ ce {{E}+{\ underset {Substrat \ atop binding} {S <=> E}} {\ overset {Catalytic \ atop step} {S-> E}}+P}}}$

Michaelis-Menten kinetik . Enzymet (E) binder et substrat (S) og producerer et produkt (P). Hver reaktion er en tilstandsovergang i en Markov -kæde.

Et reaktionsnetværk er et kemisk system, der involverer flere reaktioner og kemiske arter. De enkleste stokastiske modeller af sådanne netværk behandler systemet som en kontinuerlig Markov -kæde, hvor staten er antallet af molekyler for hver art og med reaktioner modelleret som mulige overgange af kæden. Markov-kæder og kontinuerlige Markov-processer er nyttige i kemi, når fysiske systemer nærmer sig Markov-ejendommen. Forestil dig for eksempel et stort antal n molekyler i opløsning i tilstand A, som hver kan undergå en kemisk reaktion til tilstand B med en vis gennemsnitlig hastighed. Måske er molekylet et enzym, og staterne refererer til, hvordan det foldes. Tilstanden for et enkelt enzym følger en Markov -kæde, og da molekylerne i det væsentlige er uafhængige af hinanden, er antallet af molekyler i tilstand A eller B ad gangen n gange sandsynligheden for, at et givet molekyle er i den tilstand.

Den klassiske model for enzymaktivitet, Michaelis - Menten kinetik , kan ses som en Markov -kæde, hvor reaktionen på hvert tidspunkt skrider frem i en eller anden retning. Mens Michaelis-Menten er ret ligetil, kan langt mere komplicerede reaktionsnetværk også modelleres med Markov-kæder.

En algoritme baseret på en Markov-kæde blev også brugt til at fokusere den fragmentbaserede vækst af kemikalier i silico mod en ønsket klasse af forbindelser, såsom lægemidler eller naturprodukter. Når et molekyle vokser, vælges et fragment fra det spirende molekyle som den "nuværende" tilstand. Den er ikke opmærksom på sin fortid (det vil sige, den er ikke klar over, hvad der allerede er knyttet til den). Det overgår derefter til den næste tilstand, når et fragment er knyttet til det. Overgangssandsynlighederne trænes i databaser over autentiske klasser af forbindelser.

Væksten (og sammensætningen) af copolymerer kan også modelleres ved anvendelse af Markov -kæder. Baseret på reaktivitetsforholdene for de monomerer, der udgør den voksende polymerkæde, kan kædens sammensætning beregnes (f.eks. Om monomerer har tendens til at tilføje på skiftende måde eller i lange løb af den samme monomer). På grund af steriske virkninger kan andenordens Markov-effekter også spille en rolle i væksten af ​​nogle polymerkæder.

Tilsvarende er det blevet foreslået, at krystallisationen og væksten af ​​nogle epitaksiale supergitteroxidmaterialer kan beskrives nøjagtigt af Markov -kæder.

Biologi

Markov -kæder bruges inden for forskellige områder af biologien. Bemærkelsesværdige eksempler omfatter:

• Filogenetik og bioinformatik , hvor de fleste modeller af DNA-evolution bruger kontinuerlige Markov-kæder til at beskrive nukleotidet til stede på et givet sted i genomet .
• Befolkningsdynamik , hvor Markov -kæder især er et centralt værktøj i den teoretiske undersøgelse af matrixpopulationmodeller .
• Neurobiologi , hvor Markov -kæder er blevet brugt, f.eks. Til at simulere neocortex fra pattedyr.
• Systembiologi , for eksempel med modellering af virusinfektion af enkeltceller.
• Afdelingsmodeller til sygdomsudbrud og epidemimodellering.

Test

Flere teoretikere har foreslået ideen om Markov -kædens statistiske test (MCST), en metode til at forbinde Markov -kæder til at danne et " Markov -tæppe ", arrangere disse kæder i flere rekursive lag ("wafering") og producere mere effektive testsæt - prøver - som erstatning for udtømmende test. MCST'er har også anvendelser i tidsmæssige statsbaserede netværk; Chilukuri et al .'s papir med titlen "Temporal Uncertainty Reasoning Networks for Evidence Fusion with Applications to Object Detection and Tracking" (ScienceDirect) giver en baggrund og casestudie til anvendelse af MCST'er til en bredere vifte af applikationer.

Solbestrålingsvariation

Vurderinger af variabilitet i solstråling er nyttige til applikationer med solenergi . Solbestrålingsvariabilitet på ethvert sted over tid er hovedsageligt en konsekvens af den deterministiske variation af solens vej over himmelkuppelen og variationen i uklarhed. Variabiliteten af ​​tilgængelig solindstråling på Jordens overflade er blevet modelleret ved hjælp af Markov-kæder, herunder også modellering af de to tilstande af klarhed og uklarhed som en to-staters Markov-kæde.

Tale genkendelse

Skjulte Markov -modeller er grundlaget for de fleste moderne automatiske talegenkendelsessystemer .

Informationsteori

Markov -kæder bruges under hele informationsbehandlingen. Claude Shannons berømte papir fra 1948 A Mathematical Theory of Communication , som i et enkelt trin skabte området informationsteori , åbner med at introducere begrebet entropi gennem Markov -modellering af det engelske sprog. Sådanne idealiserede modeller kan fange mange af de statistiske regelmæssigheder i systemer. Selv uden at beskrive systemets fulde struktur perfekt, kan sådanne signalmodeller muliggøre meget effektiv datakomprimering gennem entropikodningsteknikker såsom aritmetisk kodning . De tillader også effektiv statsestimering og mønstergenkendelse . Markov -kæder spiller også en vigtig rolle i forstærkningslæring .

Markov -kæder er også grundlaget for skjulte Markov -modeller, som er et vigtigt værktøj inden for så forskellige områder som telefonnetværk (der bruger Viterbi -algoritmen til fejlkorrektion), talegenkendelse og bioinformatik (f.eks. Ved registrering af omlægninger).

Den LZMA tabsfri datakomprimering algoritme kombinerer Markovkæder med Lempel-Ziv kompression for at opnå meget høje kompressionsforhold.

Køteori

Markov -kæder er grundlaget for den analytiske behandling af køer ( køteori ). Agner Krarup Erlang indledte emnet i 1917. Dette gør dem kritiske for at optimere ydelsen af ​​telekommunikationsnetværk, hvor meddelelser ofte skal konkurrere om begrænsede ressourcer (f.eks. Båndbredde).

Talrige kømodeller bruger kontinuerlige Markov-kæder. For eksempel er en M/M/1-kø en CTMC på de ikke-negative heltal, hvor opadgående overgange fra i til i  + 1 sker med hastigheden λ ifølge en Poisson-proces og beskriver jobankomster, mens overgange fra i til i  -1 (for i  > 1) forekommer med hastigheden μ (jobtiderne eksponentielt fordeles) og beskriver gennemførte tjenester (afgange) fra køen.

Internet applikationer

Et tilstandsdiagram, der repræsenterer PageRank -algoritmen med en overgangssandsynlighed for M, eller .${\ displaystyle {\ frac {\ alpha} {k_ {i}}}+{\ frac {1- \ alpha} {N}}}$

Den PageRank af en webside som bruges af Google er defineret ved en Markov kæde. Det er sandsynligheden for at være på siden i den stationære distribution på den følgende Markov -kæde på alle (kendte) websider. Hvis er antallet af kendte websider, og en side har links til den, har den overgangssandsynlighed for alle sider, der er linket til, og for alle sider, der ikke er linket til. Parameteren anses for at være omkring 0,15. ${\ displaystyle i}$${\ displaystyle N}$${\ displaystyle i}$${\ displaystyle k_ {i}}$${\ displaystyle {\ frac {\ alpha} {k_ {i}}}+{\ frac {1- \ alpha} {N}}}$${\ displaystyle {\ frac {1- \ alpha} {N}}}$${\ displaystyle \ alpha}$

Markov -modeller er også blevet brugt til at analysere brugernes webnavigeringsadfærd. En brugers weblinkovergang på et bestemt websted kan modelleres ved hjælp af første- eller andenordens Markov-modeller og kan bruges til at forudsige fremtidig navigation og tilpasse websiden til en individuel bruger.

Statistikker

Markovkædemetoder er også blevet meget vigtige for at generere sekvenser af tilfældige tal for nøjagtigt at afspejle meget komplicerede ønskede sandsynlighedsfordelinger, via en proces kaldet Markov chain Monte Carlo (MCMC). I de senere år har dette revolutioneret anvendeligheden af bayesiske inferensmetoder , hvilket har gjort det muligt at simulere en lang række posterior distributioner og finde deres parametre numerisk.

Økonomi og finans

Markov -kæder bruges inden for finansiering og økonomi til at modellere en række forskellige fænomener, herunder fordelingen af ​​indkomst, størrelsesfordelingen af ​​virksomheder, aktivpriser og markedskrascher. GD Champernowne byggede en Markov- kædemodel for indkomstfordelingen i 1953. Herbert A. Simon og medforfatter Charles Bonini brugte en Markov-kædemodel til at udlede en stationær Yule-fordeling af faste størrelser. Louis Bachelier var den første til at konstatere, at aktiekurserne fulgte tilfældigt. Den tilfældige gåtur blev senere set som bevis til fordel for effektiv-markedshypotesen, og tilfældige gå-modeller var populære i litteraturen fra 1960'erne. Regimeskiftende modeller for konjunkturcykler blev populær af James D. Hamilton (1989), der brugte en Markov-kæde til at modellere skift mellem perioder med høj og lav BNP-vækst (eller alternativt økonomiske ekspansioner og recessioner). Et nyere eksempel er Markov-switch-multifraktalmodellen af Laurent E. Calvet og Adlai J. Fisher, som bygger på bekvemmeligheden ved tidligere regime-switch-modeller. Det bruger en vilkårligt stor Markov -kæde til at drive niveauet for volatilitet i aktivafkast.

Dynamisk makroøkonomi gør stor brug af Markov -kæder. Et eksempel er at bruge Markov -kæder til eksogent at modellere aktiekurser (aktier) i en generel ligevægtsindstilling .

Kreditvurderingsbureauer producerer årlige tabeller over overgangssandsynlighederne for obligationer med forskellige kreditvurderinger.

Samfundsvidenskab

Markov-kæder bruges generelt til at beskrive stiafhængige argumenter, hvor nuværende strukturelle konfigurationer betinger fremtidige resultater. Et eksempel er reformuleringen af ​​ideen, oprindeligt på grund af Karl Marx 's Das Kapital , der knytter økonomisk udvikling til kapitalismens fremgang . I nuværende forskning er det almindeligt at bruge en Markov -kæde til at modellere, hvordan et land når et specifikt økonomisk udviklingsniveau, konfigurationen af ​​strukturelle faktorer, såsom middelklassens størrelse , forholdet mellem by og landdistrikt, satsen af politisk mobilisering osv., vil generere en større sandsynlighed for overgang fra autoritær til demokratisk regime .

Spil

Markov -kæder kan bruges til at modellere mange hasardspil. Børns spil Snakes and Ladders og " Hi Ho! Cherry-O " er f.eks. Repræsenteret præcist af Markov-kæder. Ved hver tur starter spilleren i en given tilstand (på en given firkant) og har derfra faste odds for at flytte til visse andre tilstande (firkanter).

musik

Markov -kæder anvendes i algoritmisk musikkomposition , især i software som Csound , Max og SuperCollider . I en førsteordens kæde bliver systemets tilstande note- eller pitchværdier, og en sandsynlighedsvektor for hver note er konstrueret, der fuldender en overgangssandsynlighedsmatrix (se nedenfor). En algoritme er konstrueret til at producere outputnoteværdier baseret på overgangsmatrixvægtningerne, som kan være MIDI -noteværdier, frekvens ( Hz ) eller enhver anden ønskelig metrisk.

En anden ordens Markov-kæde kan introduceres ved at overveje den aktuelle tilstand og også den tidligere tilstand, som angivet i den anden tabel. Højere, n th ordens kæder tendens til "gruppe" bemærker især sammen, mens 'brækker' i andre mønstre og sekvenser lejlighedsvis. Disse kæder af højere orden har en tendens til at generere resultater med en følelse af frasal struktur, snarere end den 'formålsløse vandring' produceret af et førsteordens system.

Markov -kæder kan bruges strukturelt, som i Xenakis's Analogique A og B. Markov -kæder bruges også i systemer, der bruger en Markov -model til at reagere interaktivt på musikindgang.

Normalt er musikalske systemer nødt til at håndhæve specifikke kontrolbegrænsninger på de sekvenser med endelig længde, de genererer, men kontrolbegrænsninger er ikke kompatible med Markov-modeller, da de fremkalder langdistanceafhængigheder, der overtræder Markov-hypotesen om begrænset hukommelse. For at overvinde denne begrænsning er der blevet foreslået en ny tilgang.

Baseball

Markov -kædemodeller har været brugt i avanceret baseballanalyse siden 1960, selvom deres brug stadig er sjælden. Hver halv-inning af et baseballspil passer til Markov-kædetilstanden, når antallet af løbere og outs betragtes. Under enhver at-bat er der 24 mulige kombinationer af antal outs og løbernes position. Mark Pankin viser, at Markov -kædemodeller kan bruges til at evaluere løb, der er skabt for både individuelle spillere og et hold. Han diskuterer også forskellige former for strategier og spillebetingelser: hvordan Markov -kædemodeller er blevet brugt til at analysere statistik for spilsituationer såsom bunting og basestjæle og forskelle, når man spiller på græs vs. AstroTurf .

Markov tekstgeneratorer

Markov-processer kan også bruges til at generere overfladisk realistisk tekst givet et eksempeldokument. Markov -processer bruges i en række forskellige rekreative " parodi generator " -software (se dissocieret presse , Jeff Harrison, Mark V. Shaney og Academias Neutronium ). Der findes flere open source-tekstgenereringsbiblioteker, der bruger Markov-kæder, herunder RiTa Toolkit .

Probabilistisk prognose

Markov -kæder er blevet brugt til prognoser på flere områder: for eksempel prisudvikling, vindkraft og solbestråling. Markov -kædens prognosemodeller anvender en række forskellige indstillinger, fra diskretisering af tidsserierne, til skjulte Markov -modeller kombineret med bølger og Markov -kædeblandingsfordelingsmodellen (MCM).

Se også

Noter

Referencer

eksterne links