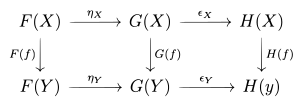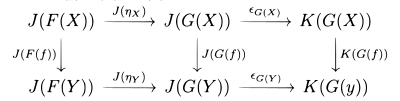Naturlig transformation - Natural transformation

I kategoriteori , en gren af matematik , giver en naturlig transformation en måde at omdanne en funktor til en anden med respekt for den interne struktur (dvs. sammensætningen af morfisme ) for de involverede kategorier . Derfor kan en naturlig transformation betragtes som en "morfisme af funktorer". Denne intuition kan faktisk formaliseres til at definere såkaldte funktorkategorier . Naturlige transformationer er, efter kategorier og funktioner, en af ​​de mest fundamentale forestillinger om kategoriteori og forekommer følgelig i de fleste af dens anvendelser.

Definition

Hvis og er funktorer mellem kategorierne og , så er en naturlig transformation fra til en familie af morfismer, der opfylder to krav. ${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle C}$${\ displaystyle D}$ ${\ displaystyle \ eta}$${\ displaystyle F}$${\ displaystyle G}$

1. Den naturlige transformation skal forbinde ethvert objekt i en morfisme mellem objekter af . Morfismen kaldes komponenten af at .${\ displaystyle X}$${\ displaystyle C}$ ${\ displaystyle \ eta _ {X}: F (X) \ til G (X)}$${\ displaystyle D}$${\ displaystyle \ eta _ {X}}$${\ displaystyle \ eta}$${\ displaystyle X}$
2. Komponenter skal være sådan, at vi for hver morfisme i har:${\ displaystyle f: X \ til Y}$${\ displaystyle C}$

${\ displaystyle \ eta _ {Y} \ circ F (f) = G (f) \ circ \ eta _ {X}}$

Den sidste ligning kan bekvemt udtrykkes ved hjælp af det kommutative diagram

Hvis begge og er modstridende , vendes de lodrette pile i dette diagram. Hvis er en naturlig transformation fra til , skriver vi også eller . Dette udtrykkes også ved at sige, at morfismefamilien er naturlig i . ${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle \ eta}$${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle \ eta: F \ til G}$${\ displaystyle \ eta: F \ indebærer G}$${\ displaystyle \ eta _ {X}: F (X) \ til G (X)}$${\ displaystyle X}$

Hvis morfismen for hvert objekt i er en isomorfisme i , siges det at være en${\ displaystyle X}$${\ displaystyle C}$${\ displaystyle \ eta _ {X}}$${\ displaystyle D}$${\ displaystyle \ eta}$ naturlig isomorfisme (eller undertidennaturlig ækvivalensellerisomorfisme af funktorer). To funktorerogkaldesnaturligt isomorfeeller simpelthenisomorfe,hvis der findes en naturlig isomorfisme fratil. ${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle F}$${\ displaystyle G}$

En infranaturlig transformation fra til er simpelthen en familie af morfismer , for alle i . Således er en naturlig transformation en infranaturlig transformation, som for hver morfisme . Den Naturalizer af , NAT , er den største underkategori af som indeholder alle de genstande af på hvilke begrænser til en naturlig transformation. ${\ displaystyle \ eta}$${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle \ eta _ {X}: F (X) \ til G (X)}$${\ displaystyle X}$${\ displaystyle C}$${\ displaystyle \ eta _ {Y} \ circ F (f) = G (f) \ circ \ eta _ {X}}$${\ displaystyle f: X \ til Y}$${\ displaystyle \ eta}$${\ displaystyle (\ eta)}$${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle \ eta}$

Eksempler

Modsat gruppe

Udtalelser som f.eks

"Hver gruppe er naturligt isomorf i forhold til sin modsatte gruppe "

florerer i moderne matematik. Vi vil nu give den præcise betydning af denne erklæring såvel som dens bevis. Betragt kategorien for alle grupper med gruppehomomorfier som morfismer. Hvis er en gruppe, definerer vi den modsatte gruppe som følger: er det samme sæt som , og operationen er defineret af . Alle multiplikationer i er således "vendt". Dannelse af den modsatte gruppe bliver en (kovariant) funktor fra til, hvis vi definerer for enhver gruppehomomorfisme . Bemærk, at det faktisk er en gruppehomomorfisme fra til : ${\ displaystyle {\ textbf {Grp}}}$${\ displaystyle (G,*)}$${\ displaystyle (G^{\ tekst {op}}, {*}^{\ tekst {op}})}$${\ displaystyle G^{\ tekst {op}}}$${\ displaystyle G}$${\ displaystyle *^{\ text {op}}}$${\ displaystyle a*^{\ text {op}} b = b*a}$${\ displaystyle G^{\ tekst {op}}}$${\ displaystyle {\ textbf {Grp}}}$${\ displaystyle {\ textbf {Grp}}}$${\ displaystyle f^{\ text {op}} = f}$${\ displaystyle f: G \ til H}$${\ displaystyle f^{\ tekst {op}}}$${\ displaystyle G^{\ tekst {op}}}$${\ displaystyle H^{\ tekst {op}}}$

${\ displaystyle f^{\ tekst {op}} (a*^{\ tekst {op}} b) = f (b*a) = f (b)*f (a) = f^{\ tekst {op }} (a)*^{\ tekst {op}} f^{\ tekst {op}} (b).}$

Indholdet af ovenstående erklæring er:

"Identitetsfunktoren er naturligt isomorf i forhold til den modsatte funktor "${\ displaystyle {\ text {Id}} _ {\ textbf {Grp}}: {\ textbf {Grp}} \ til {\ textbf {Grp}}}$${\ displaystyle {\ text {op}}: {\ textbf {Grp}} \ til {\ textbf {Grp}}}$

For at bevise dette skal vi tilvejebringe isomorfismer for hver gruppe , således at ovenstående diagram pendler. Sæt . Formlerne og viser, at det er en gruppehomomorfisme med omvendt . For at bevise naturligheden starter vi med en gruppehomomorfisme og show , altså for all in . Dette er sandt siden og hver gruppe homomorfisme har ejendommen . ${\ displaystyle \ eta _ {G}: G \ til G^{\ tekst {op}}}$${\ displaystyle G}$${\ displaystyle \ eta _ {G} (a) = a^{-1}}$${\ displaystyle (a*b)^{-1} = b^{-1}*a^{-1} = a^{-1}*^{\ text {op}} b^{-1}}$${\ displaystyle (a^{-1})^{-1} = a}$${\ displaystyle \ eta _ {G}}$${\ displaystyle \ eta _ {G^{\ text {op}}}}$${\ displaystyle f: G \ til H}$${\ displaystyle \ eta _ {H} \ circ f = f^{\ text {op}} \ circ \ eta _ {G}}$${\ displaystyle (f (a))^{-1} = f^{\ tekst {op}} (a^{-1})}$${\ displaystyle a}$${\ displaystyle G}$${\ displaystyle f^{\ text {op}} = f}$${\ displaystyle (f (a))^{-1} = f (a^{-1})}}$

Abelianisering

I betragtning af en gruppe kan vi definere dens abelianisering . Lad betegne projektionskortet på cosets af . Denne homomorfisme er "naturlig i ", dvs. den definerer en naturlig transformation, som vi nu kontrollerer. Lad være en gruppe. For enhver homomorfisme har vi det, der er indeholdt i kernen af , fordi enhver homomorfisme til en abelsk gruppe dræber kommutatorundergruppen. Derefter faktorer igennem som for den unikke homomorfisme . Dette gør en funktor og en naturlig transformation, men ikke en naturlig isomorfisme, fra identitetsfunktoren til . ${\ displaystyle G}$ ${\ displaystyle G^{\ text {ab}} = G/}$ ${\ displaystyle [G, G]}$${\ displaystyle \ pi _ {G}: G \ til G^{\ tekst {ab}}}$${\ displaystyle [G, G]}$${\ displaystyle G}$${\ displaystyle H}$${\ displaystyle f: G \ til H}$${\ displaystyle [G, G]}$${\ displaystyle \ pi _ {H} \ circ f}$${\ displaystyle \ pi _ {H} \ circ f}$${\ displaystyle G^{\ tekst {ab}}}$${\ displaystyle f^{\ text {ab}} \ circ \ pi _ {G} = \ pi _ {H} \ circ f}$${\ displaystyle f^{\ tekst {ab}}: G^{\ tekst {ab}} \ til H^{\ tekst {ab}}}$${\ displaystyle {\ text {ab}}: {\ textbf {Grp}} \ til {\ textbf {Grp}}}$${\ displaystyle \ pi}$${\ displaystyle {\ text {ab}}}$

Hurewicz homomorfisme

Funktorer og naturlige transformationer vrimler i algebraisk topologi , med Hurewicz homomorfier tjener som eksempler. For ethvert spids topologisk rum og positivt heltal eksisterer der en gruppehomomorfisme${\ displaystyle (X, x)}$${\ displaystyle n}$

${\ displaystyle h _ {*} \ colon \ pi _ {n} (X, x) \ til H_ {n} (X)}$

fra -th homotopiegruppe fra til -th homologigruppe af . Begge og er funktorer fra kategorien Top ^* af spidse topologiske rum til kategorien Grp af grupper, og er en naturlig transformation fra til . ${\ displaystyle n}$${\ displaystyle (X, x)}$${\ displaystyle n}$${\ displaystyle X}$${\ displaystyle \ pi _ {n}}$${\ displaystyle H_ {n}}$${\ displaystyle h _ {*}}$${\ displaystyle \ pi _ {n}}$${\ displaystyle H_ {n}}$

Determinant

I betragtning af kommutative ringe og med en ringhomomorfisme , arver de respektive grupper af inverterbare matricer og arver en homomorfisme, som vi betegner ved , opnået ved at anvende på hver matrixpost. Tilsvarende begrænser sig til en gruppehomomorfisme , hvor betegner gruppen af ​​enheder af . Faktisk og er funktorer fra kategorien kommutative ringe til . Den determinant på gruppen , betegnet med , er en gruppehomomorfi ${\ displaystyle R}$${\ displaystyle S}$ ${\ displaystyle f: R \ til S}$ ${\ displaystyle n \ gange n}$${\ displaystyle {\ text {GL}} _ {n} (R)}$${\ displaystyle {\ text {GL}} _ {n} (S)}$${\ displaystyle {\ text {GL}} _ {n} (f)}$${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle f^{*}: R^{*} \ til S^{*}}$${\ displaystyle R^{*}}$${\ displaystyle R}$${\ displaystyle {\ text {GL}} _ {n}}$${\ displaystyle *}$${\ displaystyle {\ textbf {CRing}}}$${\ displaystyle {\ textbf {Grp}}}$${\ displaystyle {\ text {GL}} _ {n} (R)}$${\ displaystyle {\ text {det}} _ {R}}$

${\ displaystyle {\ mbox {det}} _ {R} \ colon {\ mbox {GL}} _ {n} (R) \ til R^{*}}$

hvilket er naturligt i : fordi determinanten er defineret af den samme formel for hver ring, holder. Dette gør determinanten til en naturlig transformation fra til . ${\ displaystyle R}$${\ displaystyle f \ circ {\ text {det}} _ {R} = {\ text {det}} _ {S} \ circ {\ text {GL}} _ {n} (f)}$${\ displaystyle {\ text {GL}} _ {n}}$${\ displaystyle *}$

Dobbelt dobbelt af et vektorrum

Hvis er et felt , så har vi for hvert vektorrum over et "naturligt" injektivt lineært kort fra vektorrummet til dets dobbelte dual . Disse kort er "naturlige" i følgende forstand: den dobbelte dobbelte operation er en funktor, og kortene er komponenterne i en naturlig transformation fra identitetsfunktoren til den dobbelte dobbelte funktor. ${\ displaystyle K}$ ${\ displaystyle V}$${\ displaystyle K}$ ${\ displaystyle V \ til V^{**}}$

Endelig beregning

For hver abelsk gruppe danner sættet af funktioner fra heltalene til det underliggende sæt af en abelsk gruppe under punktvis tilføjelse. (Her er standard glemsom funktor .) I betragtning af en morfisme er kortet givet ved venstre komponering med elementerne i førstnævnte selv en homomorfisme af abelske grupper; på denne måde får vi en funktor . Den endelige forskelsoperator, der tager hver funktion til, er et kort fra sig selv, og samlingen af sådanne kort giver en naturlig transformation . ${\ displaystyle G}$${\ displaystyle {\ text {Hom}} _ {\ textbf {Set}} (\ mathbb {Z}, U (G))}$${\ displaystyle G}$${\ displaystyle V _ {\ mathbb {Z}} (G)}$${\ displaystyle U}$ ${\ displaystyle U: {\ textbf {Ab}} \ til {\ textbf {Set}}}$${\ displaystyle {\ textbf {Ab}}}$${\ displaystyle \ varphi: G \ til G '}$${\ displaystyle V _ {\ mathbb {Z}} (\ varphi): V _ {\ mathbb {Z}} (G) \ til V _ {\ mathbb {Z}} (G ')}$${\ displaystyle \ varphi}$${\ displaystyle V _ {\ mathbb {Z}}: {\ textbf {Ab}} \ til {\ textbf {Ab}}}$${\ displaystyle \ Delta _ {G}}$${\ displaystyle f: \ mathbb {Z} \ til U (G)}$${\ displaystyle \ Delta (f): n \ mapsto f (n+1) -f (n)}$${\ displaystyle V _ {\ mathbb {Z}} (G)}$${\ displaystyle \ Delta}$${\ displaystyle \ Delta: V _ {\ mathbb {Z}} \ til V _ {\ mathbb {Z}}}$

Tensor-hom-tillæg

Overvej kategorien${\ displaystyle {\ textbf {Ab}}}$ abelske grupper og gruppehomomorfier. For alle abelske grupper , og vi har en gruppe isomorfisme ${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle Z}$

${\ displaystyle {\ text {Hom}} (X \ otimes Y, Z) \ to {\ text {Hom}} (X, {\ text {Hom}} (Y, Z))}$.

Disse isomorfismer er "naturlige" i den forstand, at de definerer en naturlig transformation mellem de to involverede funktorer . (Her er "op" den modsatte kategori af , for ikke at forveksle med den trivielle modsatte gruppefunktion på  !) ${\ displaystyle {\ textbf {Ab}}^{\ text {op}} \ times {\ textbf {Ab}}^{\ text {op}} \ times {\ textbf {Ab}} \ til {\ textbf { Ab}}}$${\ displaystyle {\ textbf {Ab}}}$${\ displaystyle {\ textbf {Ab}}}$

Dette er formelt tensor-hom-adjunktet og er et arketypisk eksempel på et par tilstødende funktioner . Naturlige transformationer opstår ofte i forbindelse med tilstødende funktorer, og de tilgrænsede funktorer er faktisk defineret af en bestemt naturlig isomorfisme. Derudover er hvert par tilstødende funktioner udstyret med to naturlige transformationer (generelt ikke isomorfismer) kaldet enheden og kontakten .

Unaturlig isomorfisme

Forestillingen om en naturlig transformation er kategorisk og fastslår (uformelt), at et bestemt kort mellem funktioner kan udføres konsekvent over en hel kategori. Uformelt omtales et bestemt kort (især en isomorfisme) mellem individuelle objekter (ikke hele kategorier) som en "naturlig isomorfisme", hvilket implicit betyder, at det faktisk er defineret på hele kategorien, og definerer en naturlig transformation af funktioner; formalisering af denne intuition var en motiverende faktor i udviklingen af ​​kategoriteori. Omvendt kan et bestemt kort mellem bestemte objekter kaldes en unaturlig isomorfisme (eller "denne isomorfisme er ikke naturlig"), hvis kortet ikke kan udvides til en naturlig transformation på hele kategorien. I betragtning af et objekt en funktor (tager for enkelthed den første funktor at være identiteten) og et isomorfisme bevis på unaturlighed er lettest vist ved at give en automorfisme , der ikke pendler med denne isomorfisme (så ). Mere stærkt, hvis man ønsker at bevise det og ikke er naturligt isomorft, uden henvisning til en bestemt isomorfisme, kræver dette at vise, at for enhver isomorfisme er der nogle, som det ikke pendler med; i nogle tilfælde fungerer en enkelt automorfisme for alle kandidat -isomorfier, mens man i andre tilfælde skal vise, hvordan man konstruerer en anden for hver isomorfisme. Kortene i kategorien spiller en afgørende rolle - enhver infranaturlig transformation er naturlig, hvis de eneste kort f.eks. Er identitetskortet. ${\ displaystyle X,}$${\ displaystyle G}$${\ displaystyle \ eta \ colon X \ til G (X),}$${\ displaystyle A \ kolon X \ til X}$${\ displaystyle \ eta \ circ A \ neq G (A) \ circ \ eta}$${\ displaystyle X}$${\ displaystyle G (X)}$${\ displaystyle \ eta}$${\ displaystyle A}$${\ displaystyle A}$${\ displaystyle \ eta}$${\ displaystyle A _ {\ eta}}$

Dette ligner (men mere kategorisk) begreber i gruppeteori eller modulteori, hvor en given nedbrydning af et objekt til en direkte sum er "ikke naturlig", eller rettere "ikke unik", da der findes automorfismer, der ikke bevarer den direkte sum dekomponering - se Struktur sætning for endelig genererede moduler over et principielt ideelt domæne § Entydighed f.eks.

Nogle forfattere skelner notationsmæssigt ved hjælp af en naturlig isomorfisme og en unaturlig isomorfisme, idet de forbeholder sig lighed (normalt lighed i kort). ${\ displaystyle \ cong}$${\ displaystyle \ approx}$${\ displaystyle =}$

Eksempel: grundlæggende gruppe af torus

Som et eksempel på sondringen mellem funktoriel erklæring og individuelle objekter, overvej homotopigrupper i et produktrum, specifikt torusens grundlæggende gruppe.

De homotopigrupper af et produkt rum er naturligvis produktet af de homotopigrupper af komponenterne, med isomorfi givet ved projektion på de to faktorer, fundamentalt fordi afbildes i et produkt rum er nøjagtigt produkter af mapper til komponenterne - dette er en functorial udmelding. ${\ displaystyle \ pi _ {n} ((X, x_ {0}) \ times (Y, y_ {0})) \ cong \ pi _ {n} ((X, x_ {0})) \ times \ pi _ {n} ((Y, y_ {0})),}$

Torus (som abstrakt er et produkt af to cirkler) har imidlertid en grundlæggende gruppe isomorf til , men opdelingen er ikke naturlig. Bemærk brugen af , og : ${\ displaystyle Z^{2}}$${\ displaystyle \ pi _ {1} (T, t_ {0}) \ approx \ mathbf {Z} \ times \ mathbf {Z}}$${\ displaystyle \ approx}$${\ displaystyle \ cong}$${\ displaystyle =}$

${\ displaystyle \ pi _ {1} (T, t_ {0}) \ approx \ pi _ {1} (S^{1}, x_ {0}) \ gange \ pi _ {1} (S^{1 }, y_ {0}) \ cong \ mathbf {Z} \ times \ mathbf {Z} = \ mathbf {Z} ^{2}.}$

Denne abstrakte isomorfisme med et produkt er ikke naturlig, da nogle isomorfier af ikke bevarer produktet: selvhomeomorfismen af (tænkt som kvotrummet ) givet af (geometrisk et Dehn-twist om en af ​​de genererende kurver) fungerer som dette matrix on (det er i den generelle lineære gruppe af inverterbare heltalmatricer), som ikke bevarer nedbrydningen som et produkt, fordi det ikke er diagonal. Men hvis man får torus som et produkt - ækvivalent, givet en dekomponering af rummet - så følger opdelingen af ​​gruppen fra den generelle erklæring tidligere. I kategoriske termer er den relevante kategori (bevarelse af et produktrums struktur) "kort over produktrum, nemlig et par kort mellem de respektive komponenter". ${\ displaystyle T}$${\ displaystyle T}$ ${\ displaystyle R ^{2}/\ mathbb {Z} ^{2}}$${\ displaystyle \ left ({\ begin {smallmatrix} 1 & 1 \\ 0 & 1 \ end {smallmatrix}} \ right)}$${\ displaystyle \ mathbb {Z} ^{2}}$ ${\ displaystyle {\ text {GL}} (\ mathbb {Z}, 2)}$${\ displaystyle (T, t_ {0}) = (S^{1}, x_ {0}) \ gange (S^{1}, y_ {0})}$

Naturlighed er en kategorisk opfattelse og kræver at være meget præcis med hensyn til præcis hvilke data der gives - torus som et rum, der tilfældigvis er et produkt (i kategorien mellemrum og kontinuerlige kort) er forskelligt fra torus præsenteret som et produkt (i kategorien af ​​produkter med to mellemrum og kontinuerlige kort mellem de respektive komponenter).

Eksempel: dobbelt af et endeligt-dimensionelt vektorrum

Hvert endeligt-dimensionelt vektorrum er isomorft i forhold til dets dobbelte rum, men der kan være mange forskellige isomorfier mellem de to rum. Der er generelt ingen naturlig isomorfisme mellem et endeligt-dimensionelt vektorrum og dets dobbelte rum. Imidlertid har relaterede kategorier (med yderligere struktur og begrænsninger på kortene) en naturlig isomorfisme, som beskrevet nedenfor.

Dobbeltrummet i et endeligt-dimensionelt vektorrum er igen et endeligt-dimensionelt vektorrum med samme dimension, og disse er således isomorfe, da dimension er den eneste invariant af endelige-dimensionelle vektorrum over et givet felt. Men i mangel af yderligere begrænsninger (f.eks. Et krav om, at kort bevarer det valgte grundlag), er kortet fra et rum til dets dual ikke unikt, og derfor kræver en sådan isomorfisme et valg og er "ikke naturligt". På kategorien endelige-dimensionelle vektorrum og lineære kort kan man definere en infranaturlig isomorfisme fra vektorrum til deres dual ved at vælge en isomorfisme for hvert rum (f.eks. Ved at vælge et grundlag for hvert vektorrum og tage den tilsvarende isomorfisme), men dette vil ikke definere en naturlig transformation. Intuitivt er det fordi det krævede et valg, grundigt fordi ethvert sådant valg af isomorfismer ikke vil pendle med f.eks. Nulkortet; se ( Mac Lane & Birkhoff 1999 , §VI.4) for detaljeret diskussion.

Ud fra endelige-dimensionelle vektorrum (som objekter) og identiteten og de dobbelte funktioner kan man definere en naturlig isomorfisme, men dette kræver først at tilføje yderligere struktur og derefter begrænse kortene fra "alle lineære kort" til "lineære kort, der respekterer dette struktur". Udtrykkeligt for hver vektor plads, kræver, at det kommer med data fra en isomorfi dets dobbelte, . Med andre ord, tag som objekter vektorrum med en ikke -genereret bilinear form . Dette definerer en infranaturlig isomorfisme (isomorfisme for hvert objekt). Man begrænser derefter kortene til kun de kort, der pendler med isomorfier: eller med andre ord, bevarer bilineær formular: . (Disse kort definerer isomorfismernes naturalisator .) Den resulterende kategori, med objekter endelige-dimensionelle vektorrum med en ikke-degenereret bilinear form, og kortlægger lineære transformationer, der respekterer den bilinære form, har ved konstruktion en naturlig isomorfisme fra identiteten til den dobbelte (hvert rum har en isomorfisme til sin dobbelte, og kortene i kategorien skal pendle). Set i dette lys er denne konstruktion (tilføj transformer for hvert objekt, begræns kort til pendling med disse) helt generel og afhænger ikke af særlige egenskaber ved vektorrum. ${\ displaystyle \ eta _ {V} \ kolon V \ til V^{*}}$ ${\ displaystyle b_ {V} \ kolon V \ gange V \ til K}$${\ displaystyle T \ kolon V \ til U}$${\ displaystyle T^{*} (\ eta _ {U} (T (v))) = \ eta _ {V} (v)}$${\ displaystyle b_ {U} (T (v), T (w)) = b_ {V} (v, w)}$

I denne kategori (endelige-dimensionelle vektorrum med en ikke-degenereret bilinear form, kortlægger lineære transformationer, der respekterer den bilinear form), kan dual af et kort mellem vektorrum identificeres som en transponering . Ofte af hensyn til geometrisk interesse er dette specialiseret til en underkategori ved at kræve, at de ikke -degenererede bilinære former har yderligere egenskaber, såsom at være symmetriske ( ortogonale matricer ), symmetriske og positive bestemte ( indre produktrum ), symmetrisk sesquilinear ( hermitiske rum ), skæv-symmetrisk og totalt isotrop ( symplektisk vektorrum ) osv.-i alle disse kategorier er et vektorrum naturligt identificeret med dets dobbelte, af den ikke-genererede bilinære form.

Operationer med naturlige transformationer

Horisontal og lodret sammensætning af naturlige transformationer

Hvis og er naturlige transformationer mellem funktorer , så kan vi komponere dem for at få en naturlig transformation . Dette gøres componentwise: . ${\ displaystyle \ eta: F \ til G}$${\ displaystyle \ epsilon: G \ til H}$${\ displaystyle F, G, H: C \ til D}$${\ displaystyle \ epsilon \ eta: F \ til H}$${\ displaystyle (\ epsilon \ eta) _ {X} = \ epsilon _ {X} \ eta _ {X}}$

Denne "lodrette sammensætning" af naturlig transformation er associativ og har en identitet og giver mulighed for at betragte samlingen af ​​alle funktioner selv som en kategori (se nedenfor under Functor -kategorier ). ${\ displaystyle C \ til D}$

Naturlige transformationer har også en "vandret sammensætning". Hvis er en naturlig transformation mellem funktorer og er en naturlig transformation mellem funktorer , tillader sammensætningen af ​​funktorer en sammensætning af naturlige transformationer, hvor . ${\ displaystyle \ eta: F \ til G}$${\ displaystyle F, G: C \ til D}$${\ displaystyle \ epsilon: J \ til K}$${\ displaystyle J, K: D \ til E}$${\ displaystyle \ epsilon *\ eta: JF \ til KG}$${\ displaystyle (\ epsilon \ ast \ eta) _ {X} = \ epsilon _ {G (X)} J (\ eta _ {X})}$

Denne operation er også associativ med identitet, og identiteten falder sammen med den for lodret sammensætning. De to operationer er relateret til en identitet, der udveksler lodret sammensætning med vandret sammensætning: hvis vi har fire naturlige transformationer som vist på billedet til højre, gælder følgende identitet ${\ displaystyle \ alpha, \ alpha ', \ beta, \ beta'}$

${\ displaystyle (\ beta '\ alpha')*(\ beta \ alpha) = (\ beta '*\ beta) (\ alpha'*\ alpha).}$

Hvis er en naturlig transformation mellem funktorer og er en anden funktor, så kan vi danne den naturlige transformation ved at definere ${\ displaystyle \ eta: F \ til G}$${\ displaystyle F, G: C \ til D}$${\ displaystyle H: D \ til E}$${\ displaystyle H \ eta: HF \ til HG}$

${\ displaystyle (H \ eta) _ {X} = H (\ eta _ {X}).}$

Hvis på den anden side er en funktor, er den naturlige transformation defineret af ${\ displaystyle K: B \ til C}$${\ displaystyle \ eta K: FK \ til GK}$

${\ displaystyle (\ eta K) _ {X} = \ eta _ {K (X)}.}$

Functor kategorier

Hvis der er en kategori og er en lille kategori , kan vi danne funktorkategorien, der som objekter har alle funktorer fra til og som morfisme de naturlige transformationer mellem disse funktorer. Dette danner en kategori, da der for enhver funktor er en identisk naturlig transformation (som tildeler ethvert objekt identitetsmorfismen på ), og sammensætningen af ​​to naturlige transformationer ("vertikal sammensætning" ovenfor) er igen en naturlig transformation. ${\ displaystyle C}$${\ displaystyle I}$ ${\ displaystyle C^{I}}$${\ displaystyle I}$${\ displaystyle C}$${\ displaystyle F}$${\ displaystyle 1_ {F}: F \ til F}$${\ displaystyle X}$${\ displaystyle F (X)}$

De isomorfier i er netop de naturlige isomorfier. Det vil sige, en naturlig transformation er en naturlig isomorfisme, hvis og kun hvis der eksisterer en naturlig transformation, sådan at og . ${\ displaystyle C^{I}}$${\ displaystyle \ eta: F \ til G}$${\ displaystyle \ epsilon: G \ til F}$${\ displaystyle \ eta \ epsilon = 1_ {G}}$${\ displaystyle \ epsilon \ eta = 1_ {F}}$

Funktorkategorien er især nyttig, hvis den stammer fra en rettet graf . For eksempel, hvis er kategorien af den orienterede graf • → • , så har som objekter de morfier af , og en morphism mellem og i er et par morfier og i sådan, at de "firkantede pendler", dvs. . ${\ displaystyle C^{I}}$${\ displaystyle I}$${\ displaystyle I}$${\ displaystyle C^{I}}$${\ displaystyle C}$${\ displaystyle \ phi: U \ til V}$${\ displaystyle \ psi: X \ til Y}$${\ displaystyle C^{I}}$${\ displaystyle f: U \ til X}$${\ displaystyle g: V \ til Y}$${\ displaystyle C}$${\ displaystyle \ psi \ circ f = g \ circ \ phi}$

Mere generelt kan man bygge 2-kategorien hvis ${\ displaystyle {\ textbf {Cat}}}$

• 0-celler (objekter) er de små kategorier,
• 1-celler (pile) mellem to objekter og er funktionerne fra til ,${\ displaystyle C}$${\ displaystyle D}$${\ displaystyle C}$${\ displaystyle D}$
• 2-celler mellem to 1-celler (funktorer) og er de naturlige transformationer fra til .${\ displaystyle F: C \ til D}$${\ displaystyle G: C \ til D}$${\ displaystyle F}$${\ displaystyle G}$

De vandrette og lodrette sammensætninger er sammensætningerne mellem naturlige transformationer beskrevet tidligere. En funktorkategori er så simpelthen en hjemmekategori i denne kategori (små spørgsmål til side). ${\ displaystyle C^{I}}$

Flere eksempler

Hver grænse og grænse giver et eksempel på en simpel naturlig transformation, da en kegle udgør en naturlig transformation med den diagonale funktor som domæne. Hvis grænser og kolimitter er defineret direkte med hensyn til deres universelle egenskab , er de faktisk universelle morfisme i en funktorkategori.

Yoneda lemma

Hvis er et objekt i en lokalt lille kategori , definerer opgaven en kovariant funktor . Denne funktor kaldes repræsentabel (mere generelt er en repræsentabel funktor enhver funktor, der er naturligt isomorf for denne funktor for et passende valg af ). De naturlige transformationer fra en repræsentabel funktor til en vilkårlig funktor er fuldstændig kendte og lette at beskrive; dette er indholdet af Yoneda -lemmaet . ${\ displaystyle X}$ ${\ displaystyle C}$${\ displaystyle Y \ mapsto {\ text {Hom}} _ {C} (X, Y)}$${\ displaystyle F_ {X}: C \ til {\ textbf {Set}}}$${\ displaystyle X}$${\ displaystyle F: C \ til {\ textbf {Set}}}$

Historiske noter

Saunders Mac Lane , en af ​​grundlæggerne af kategoriteori, siges at have bemærket: "Jeg opfandt ikke kategorier for at studere funktorer; jeg opfandt dem for at studere naturlige transformationer." Ligesom studiet af grupper ikke er fuldstændigt uden en undersøgelse af homomorfismer , er studiet af kategorier ikke fuldendt uden studiet af funktorer . Årsagen til Mac Lanes kommentar er, at studiet af funktorer i sig selv ikke er færdigt uden studiet af naturlige transformationer.

Konteksten for Mac Lanes bemærkning var den aksiomatiske teori om homologi . Forskellige måder at konstruere homologi kunne vise sig at falde sammen: for eksempel i tilfælde af et forenklet kompleks ville de grupper, der defineres direkte, være isomorfe i forhold til dem i entallsteorien. Hvad der ikke let kan udtrykkes uden sproget i naturlige transformationer er, hvordan homologigrupper er kompatible med morfisme mellem objekter, og hvordan to ækvivalente homologiteorier ikke kun har de samme homologigrupper, men også de samme morfismer mellem disse grupper.

Se også

• Ekstranaturlig transformation
• Universel ejendom
• Højere kategoriteori

Noter

Referencer

eksterne links

• nLab , et wikiprojekt om matematik, fysik og filosofi med vægt på det n -kategoriske synspunkt
• André Joyal , CatLab , et wiki -projekt dedikeret til fremlæggelse af kategorisk matematik
• Hillman, Chris. "En kategorisk primer". CiteSeerX  10.1.1.24.3264 : Manglende eller tom |url=( hjælp ) formel introduktion til kategoriteori.
• J. Adamek, H. Herrlich, G. Stecker, Abstrakt og konkrete kategorier-Kattens glæde
• Stanford Encyclopedia of Philosophy : " Category Theory "-af Jean-Pierre Marquis. Omfattende bibliografi.
• Liste over akademiske konferencer om kategoriteori
• Baez, John, 1996, " Fortællingen om n -kategorier. " En uformel introduktion til højere kategorier.
• WildCats er en kategoriteori -pakke til Mathematica . Manipulation og visualisering af objekter, morfisme , kategorier, funktorer , naturlige transformationer, universelle egenskaber .
• The catsters , en YouTube -kanal om kategoriteori.
• Videoarkiv med indspillede samtaler, der er relevante for kategorier, logik og fysikkens grundlag.
• Interaktiv webside, der genererer eksempler på kategoriske konstruktioner i kategorien endelige sæt.