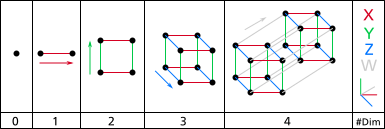Tesseract - Tesseract

Tesseract 8-celle 4-terning
Schlegel diagram
Type	Konveks almindelig 4-polytop
Schläfli -symbol	{4,3,3} t 0,3 {4,3,2} eller {4,3} × {} t 0,2 {4,2,4} eller {4} × {4} t 0,2 , 3 {4,2,2} eller {4} × {} × {} t 0,1,2,3 {2,2,2} eller {} × {} × {} × {}
Coxeter diagram
Celler	8 {4,3}
Ansigter	24 {4}
Kanter	32
Hjørner	16
Vertex figur	Tetraeder
Petrie polygon	ottekant
Coxeter gruppe	B 4 , [3,3,4]
Dobbelt	16-celle
Ejendomme	konveks , isogonal , isotoksal , isohedral
Ensartet indeks	10

Den Dali kors , en netto af en tesseract

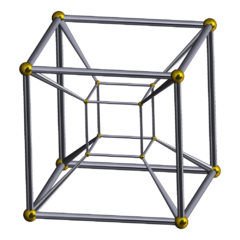
I geometri er tesserakten den firdimensionelle analog af terningen ; tesseract er til terningen, som terningen er til firkanten . Ligesom overfladen af terningen består af seks firkantede ansigter , den hyperoverflade af tesseract består af otte kubisk celler . Tesseract er en af ​​de seks konvekse regelmæssige 4-polytoper .

Tesserakten kaldes også en 8-celle , C ₈ , (almindelig) octachoron , octahedroid , kubisk prisme og tetracube . Det er den fire-dimensionelle hypercube , eller 4-terning som medlem af den dimensionelle familie af hypercubes eller måle polytoper . Coxeter mærker det som polytopen. Udtrykket hyperkube uden en dimensionsreference behandles ofte som et synonym for denne specifikke polytop . ${\ displaystyle \ gamma _ {4}}$

Ifølge Oxford English Dictionary blev ordet tesseract først brugt i 1888 af Charles Howard Hinton i sin bog A New Era of Thought , fra den græske téssara ( τέσσαρα 'fire') og aktís ( ἀκτίς 'ray'), med henvisning til fire kanter fra hvert toppunkt til andre hjørner. I denne publikation samt nogle af Hintons senere værker blev ordet lejlighedsvis stavet tessarakt .

Geometri

Tesserakten kan konstrueres på en række måder. Som en almindelig polytop med tre terninger foldet sammen rundt om hver kant har den Schläfli -symbolet {4,3,3} med hyperoktadrisk symmetri af orden 384. Konstrueret som et 4D -hyperprisme lavet af to parallelle terninger, kan det navngives som en sammensat Schläfli symbolet {4,3} × {}, med symmetriordre 96. Som et 4-4- duopris , et kartesisk produkt af to firkanter , kan det navngives med et sammensat Schläfli-symbol {4} × {4} med symmetriordre 64 . Som en ortotop kan den repræsenteres ved sammensat Schläfli -symbol {} × {} × {} × {} eller {} ⁴ med symmetriordre 16.

Da hvert hjørne af en tesseract støder op til fire kanter, er tesseractens toppunkt en regulær tetraeder . Den dobbelte polytop af tesseract er 16-celle med Schläfli symbol {3,3,4}, med hvilken den kan kombineres til dannelse af forbindelsen med tesseract og 16-celle .

Koordinater

Standard tesseract i euklidisk 4-mellemrum er angivet som punkternes konvekse skrog (± 1, ± 1, ± 1, ± 1). Det vil sige, at den består af punkterne:

${\ displaystyle \ {(x_ {1}, x_ {2}, x_ {3}, x_ {4}) \ in \ mathbb {R} ^{4} \,: \,-1 \ leq x_ {i} \ leq 1 \}}$

I denne kartesiske referenceramme har tesserakten radius 2 og er afgrænset af otte hyperplaner ( x _i = ± 1). Hvert par ikke-parallelle hyperplaner skærer hinanden og danner 24 firkantede flader i en tesseract. Tre terninger og tre firkanter skærer hinanden i hver kant. Der er fire terninger, seks firkanter og fire kanter, der mødes ved hvert toppunkt. Alt i alt består den af ​​8 terninger, 24 firkanter, 32 kanter og 16 hjørner.

Fremskrivninger til to dimensioner

En animation af forskydningen i dimensioner

Konstruktionen af hypercubes kan forestilles på følgende måde:

• 1-dimensionel: To punkter A og B kan forbindes til en linje, hvilket giver et nyt linjesegment AB.
• 2-dimensionel: To parallelle linjesegmenter AB og CD kan forbindes til en firkant med hjørnerne markeret som ABCD.
• 3-dimensionel: To parallelle firkanter ABCD og EFGH kan forbindes til en terning, med hjørnerne markeret som ABCDEFGH.
• 4-dimensionel: To parallelle terninger ABCDEFGH og IJKLMNOP kan forbindes til en tesseract, med hjørnerne markeret som ABCDEFGHIJKLMNOP.

Et diagram, der viser, hvordan man opretter en tesseract fra et punkt

En 3D-projektion af en 8-celle, der udfører en simpel rotation omkring et plan, der skærer figuren fra for-venstre til bag-højre og top til bund

Det er muligt at projektere tesseracts i tre- og todimensionale rum, på samme måde som at projicere en terning i todimensionalt rum.

Fremskrivninger på 2D-planet bliver mere lærerige ved at omarrangere positionerne af de projicerede hjørner. På denne måde kan man opnå billeder, der ikke længere afspejler de rumlige forhold inden for tesseracten, men som illustrerer forbindelsesstrukturen for hjørnerne, såsom i følgende eksempler:

En tesseract opnås i princippet ved at kombinere to terninger. Skemaet ligner konstruktionen af ​​en terning fra to firkanter: sidestill to kopier af den nedre dimensionelle terning, og forbind de tilsvarende hjørner. Hver kant af en tesseract er af samme længde. Denne opfattelse er interessant, når man bruger tesseracts som grundlag for en netværkstopologi til at forbinde flere processorer i parallel computing : afstanden mellem to noder er højst 4, og der er mange forskellige veje, der tillader vægtbalancering.

Parallelle fremspring til 3 dimensioner

Parallelle projektionskonvolutter af tesserakten (hver celle tegnes med forskellige farveflader, inverterede celler er ikke tegnet)

Den celle-første parallelle projektion af tesserakten ind i det tredimensionelle rum har en kubisk konvolut. De nærmeste og fjerneste celler projiceres på terningen, og de resterende seks celler projiceres på terningens seks firkantede flader.

Den første parallelle projektion af tesserakten ind i det tredimensionelle rum har en kubisk konvolut. To par celler rager ud til den øvre og nedre halvdel af denne kuvert, og de fire resterende celler rager ud til siderne.

Den kant-første parallelle projektion af tesserakten ind i det tredimensionelle rum har en konvolut i form af et sekskantet prisme . Seks celler projekterer på rhombiske prismer, som er lagt ud i det sekskantede prisme på en måde, der er analog med, hvordan 3D-terningens flader rager ud på seks romber i en sekskantet konvolut under toppunkt-første projektion. De to resterende celler projekterer på prisme -baserne.

Den rhombiske dodecahedron danner det konvekse skrog af tesseractens vertex-første parallelle projektion. Antallet af hjørner i lagene i dette projektion er 1 4 6 4 1 - den fjerde række i Pascals trekant .

Den toppunkt-første parallelle projektion af tesserakten ind i det tredimensionelle rum har en rhombisk dodecahedral kuvert. To hjørner af tesserakten projiceres til oprindelsen. Der er præcis to måder at dissekere en rhombisk dodecahedron i fire kongruente rhomboeder , hvilket giver i alt otte mulige rhomboeder, hver en projiceret terning af tesserakten. Denne projektion er også den med maksimal volumen. Et sæt projektionsvektorer er u = (1,1, -1, -1), v = (-1,1, -1,1), w = (1, -1, -1,1).

Som en konfiguration

Denne konfigurationsmatrix repræsenterer tesseract. Rækkerne og kolonnerne svarer til hjørner, kanter, flader og celler. De diagonale tal siger, hvor mange af hvert element der forekommer i hele tesserakten. De ikke -diagonale tal siger, hvor mange af kolonnens element, der forekommer i eller ved rækkeens element. For eksempel angiver 2'et i den første kolonne i den anden række, at der er 2 hjørner i (dvs. yderst på) hver kant; 4 i den anden kolonne i den første række angiver, at 4 kanter mødes ved hvert toppunkt.

${\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 16 & 4 & 6 & 4 \\ 2 & 32 & 3 & 3 \\ 4 & 4 & 24 & 2 \\ 8 & 12 & 6 & 8 \ end {matrix}} \ end {bmatrix}}}$

Billedgalleri

Tesserakten kan foldes ud i otte terninger til 3D -rum, ligesom terningen kan foldes ud i seks firkanter til 2D -rum. En udfoldelse af en polytop kaldes et net . Der er 261 forskellige net af tesserakten. Tesseractens udfoldelser kan tælles ved at kortlægge netene til parrede træer (et træ sammen med en perfekt matchning i sit komplement ).

Stereoskopisk 3D -projektion af en tesseract (parallelvisning)

Alternative fremskrivninger

En 3D -projektion af en tesseract, der udfører en dobbelt rotation omkring to ortogonale planer

Afspil medier 3D -projektion af tre tesseracts med og uden ansigter

Perspektiv med fjernelse af skjult volumen . Det røde hjørne er det nærmeste i 4D og har 4 kubiske celler, der mødes omkring det.

De tetrahedron danner konvekse skrog af tesseract s toppunkt-centreret centrale fremspring. Fire af 8 kubiske celler er vist. Det 16. toppunkt projiceres i det uendelige, og de fire kanter til det er ikke vist.

Stereografisk projektion (Kanterne projiceres på 3-kuglen )

Animation, der viser de enkelte terning i B ₄ Coxeter plan projektion af tesseract.

2D ortografiske fremskrivninger

Ortografiske fremskrivninger

Coxeter fly	B 4	B 3 / D 4 / A 2	B 2 / D 3
Kurve
Dihedral symmetri	[8]	[6]	[4]
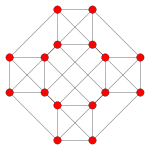
Coxeter fly	Andet	F 4	A 3
Kurve
Dihedral symmetri	[2]	[12/3]	[4]

Bevis uden ord om , at tesseract-grafen er ikke-plan ved hjælp af Kuratowskis eller Wagners sætninger og finder enten K ₅ (top) eller K _3,3 (nederste) undergrafer

Radial ligesidet symmetri

Tesseractens lange radius (fra midten til toppunktet) er lig med dens kantlængde; således er dens diagonal gennem midten (toppunkt til modsat toppunkt) 2 kantlængder. Kun få ensartede polytoper har denne egenskab, herunder den fire-dimensionelle tesseract og 24-celle , den tredimensionelle cuboctahedron og den todimensionale hexagon . Især tesseract er den eneste hyperkube (bortset fra et 0-dimensionelt punkt) med denne egenskab. Den længste vertex-to-vertex-diameter af en n -dimensionel hyperkube med enheds kantlængde er √ n , så for kvadratet er det √ 2 , for terningen er det √ 3 , og kun for tesseract er det √ 4 , præcis 2 kantlængder.

Tessellation

Tesseracten, som alle hypercubes , tessellerer det euklidiske rum . Den selvdobbelte tesseraktiske bikage bestående af 4 tesseracts omkring hvert ansigt har Schläfli- symbolet {4,3,3,4} . Derfor har tesserakten en dihedral vinkel på 90 °.

Tesseractens radiale ligesidede symmetri gør dens tessellation til det unikke regelmæssige kropscentrerede kubiske gitter af kugler af samme størrelse i et vilkårligt antal dimensioner.

Selve tesserakten kan nedbrydes til mindre polytoper. Det er det konvekse skrog af forbindelsen af ​​to demitesseracts ( 16-celler ). Tesserakten kan også trianguleres til 4-dimensionelle simplekser, der deler deres hjørner med tesserakten. Det vides, at der er 92487256 sådanne trianguleringer, og at de færreste 4-dimensionelle enkeltheder i nogen af ​​dem er 16.

Formler

For en tesseract med sidelængde s :

• Hypervolumen: ${\ displaystyle H = s^{4}}$
• Overflade volumen: ${\ displaystyle SV = 8s^{3}}$
• Ansigt diagonal :${\ displaystyle d _ {\ mathrm {2}} = {\ sqrt {2}} s}$
• Celle diagonal :${\ displaystyle d _ {\ mathrm {3}} = {\ sqrt {3}} s}$
• 4-rums diagonal: ${\ displaystyle d _ {\ mathrm {4}} = 2s}$

Relaterede polytoper og honningkager

Tesserakten (8-celle) er den tredje i sekvensen af ​​6 konvekse regelmæssige 4-polytoper (i rækkefølge efter størrelse og kompleksitet).

Regelmæssige konvekse 4-polytoper
Symmetri gruppe	A 4	B 4		F 4	H 4
Navn	5-celle Hyper- tetraeder	16-celle hyper- oktaeder	8-celle Hyper- terning	24-celle	600-celle Hyper- icosahedron	120-celle hyper- dodekaeder
Schläfli -symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter diagram
Kurve
Hjørner	5	8	16	24	120	600
Kanter	10	24	32	96	720	1200
Ansigter	10 trekanter	32 trekanter	24 firkanter	96 trekanter	1200 trekanter	720 femkanter
Celler	5 tetraeder	16 tetraeder	8 terninger	24 oktaedra	600 tetraeder	120 dodecahedra
Lang radius	1	1	1	1	1	1
Kantlængde	√ 5/√ 2 ≈ 1,581	√ 2 ≈ 1.414	1	1	1/ϕ ≈ 0,618	1/√ 2 ϕ 2 ≈ 0,270
Kort radius	1/4	1/2	1/2	√ 2/2 0,707	1 - (√ 2/2 √ 3 φ) 2 ≈ 0,936	1 - (1/2 √ 3 φ) 2 ≈ 0,968
Areal	10 •√ 8/3 ≈ 9.428	32 •√ 3/4 ≈ 13,856	24	96 •√ 3/8 ≈ 20.785	1200 •√ 3/8φ 2 ≈ 99.238	720 •25+10 √ 5/8φ 4 ≈ 621,9
Bind	5 •5 √ 5/24 2,329	16 •1/3 ≈ 5.333	8	24 •√ 2/3 ≈ 11.314	600 •1/3 √ 8 φ 3 .6 16.693	120 •2 + φ/2 √ 8 φ 3 ≈ 18.118
4-indhold	√ 5/24• (√ 5/2) 4 ≈ 0,146	2/3 ≈ 0,667	1	2	Kort ∙ bind/4 3,907	Kort ∙ bind/4 4,385

Som en ensartet duopisme eksisterer tesserakten i en række ensartede duoprismer : { p } × {4}.

Den almindelige tesseract, sammen med 16-cellen , findes i et sæt af 15 ensartede 4-polytoper med samme symmetri . Tesserakten {4,3,3} findes i en sekvens af regelmæssige 4-polytoper og honningkager , { p , 3,3} med tetraedriske vertex-figurer , {3,3}. Tesserakten er også i en sekvens af regelmæssige 4-polytoper og honningkager , {4,3, p } med kubiske celler .

Ortogonal	Perspektiv
4 {4} 2 , med 16 hjørner og 8 4-kanter, med de 8 4-kanter vist her som 4 røde og 4 blå firkanter.

Den almindelige komplekse polytop ₄ {4} ₂ ,, in har en reel repræsentation som en tesseract eller 4-4 duoprisme i 4-dimensionelt rum. ₄ {4} ₂ har 16 hjørner og 8 4-kanter. Dens symmetri er ₄ [4] ₂ , rækkefølge 32. Den har også en lavere symmetri -konstruktion,${\ displaystyle \ mathbb {C} ^{2}}$, eller ₄ {} × ₄ {}, med symmetri ₄ [2] ₄ , rækkefølge 16. Dette er symmetrien, hvis de røde og blå 4-kanter anses for at være forskellige.

I populærkulturen

Siden deres opdagelse har fire-dimensionelle hyperkuber været et populært tema inden for kunst, arkitektur og science fiction. Bemærkelsesværdige eksempler omfatter:

• " And He Built a Crooked House ", Robert Heinleins science fiction-historie fra 1940 med en bygning i form af en fire-dimensionel hypercube. Dette og Martin Gardners "The No-Sided Professor", udgivet i 1946, er blandt de første inden for science fiction, der introducerede læserne til Moebius-bandet , Klein-flasken og hypercube (tesseract).
• Korsfæstelse (Corpus Hypercubus) , et oliemaleri fra 1954 af Salvador Dalí med en firdimensionel hyperkube udfoldet til et tredimensionelt latinsk kors .
• Den Grande Arche , et monument og bygning nær Paris, Frankrig, der blev afsluttet i 1989. Ifølge monumentets ingeniør, Erik Reitzel , Grande Arche er designet til at ligne projektionen af en hyperkubus.
• Fez , et videospil, hvor man spiller en karakter, der kan se ud over de to dimensioner, andre tegn kan se, og skal bruge denne evne til at løse platformspil. Indeholder "Dot", en tesseract, der hjælper spilleren med at navigere rundt i verden og fortæller, hvordan man bruger evner, der passer til temaet at se ud over menneskelig opfattelse af kendt dimensionelt rum.

Ordet tesseract blev senere vedtaget til talrige andre anvendelser i populærkulturen, herunder som en plot-enhed i science fiction-værker, ofte med ringe eller ingen forbindelse til denne artikels fire-dimensionelle hyperkube. Se Tesseract (disambiguation) .

Se også

• Matematik og kunst

Noter

Referencer

• Coxeter, HSM (1973). Regular Polytopes (3. udgave). New York: Dover. s.  122 –123.
• F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss (1995) Kaleidoscopes: Selected Writings of HSM Coxeter , Wiley-Interscience Publication ISBN  978-0-471-01003-6 [1]
  • (Papir 22) HSM Coxeter, Regular and Semi Regular Polytopes I , Mathematische Zeitschrift 46 (1940) 380–407, MR 2,10]
  • (Papir 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
  • (Papir 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
• John H. Conway , Heidi Burgiel, Chaim Goodman-Strass (2008) The Symmetries of Things , ISBN  978-1-56881-220-5 (kapitel 26. s. 409: Hemicubes: 1 _n1 )
• T. Gosset (1900) On the Regular and Semi-Regular Figures in Space of n Dimensions , Messenger of Mathematics , Macmillan.
• T. Proctor Hall (1893) "Projektionen af ​​firefoldede figurer på en tre-flad" , American Journal of Mathematics 15: 179–89.
• Norman Johnson Uniform Polytopes , Manuscript (1991)
  • NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D. (1966)
• Victor Schlegel (1886) Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper , Waren.

eksterne links

• Weisstein, Eric W. "Tesseract" . MathWorld .
• Klitzing, Richard. "4D ensartede polytoper (polychora) x4o3o3o - tes" .
• Tesseract Ray spores billeder med skjult overfladeeliminering. Dette websted giver en god beskrivelse af metoder til visualisering af 4D -faste stoffer.
• Der 8-Zeller (8-cellers) Marco Möllers regelmæssige polytoper i ℝ ⁴ (tysk)
• WikiChoron: Tesseract
• HyperSolids er et open source-program til Apple Macintosh (Mac OS X og nyere), der genererer de fem regelmæssige faste stoffer i det tredimensionelle rum og de seks almindelige hypersolider i det fire-dimensionelle rum.
• Hypercube 98 Et Windows -program, der viser animerede hypercubes, af Rudy Rucker
• ken perlins hjemmeside En måde at visualisere hypercubes af Ken Perlin
• Nogle noter om den fjerde dimension indeholder animerede selvstudier om flere forskellige aspekter af tesserakten af Davide P. Cervone
• Tesseract -animation med fjernelse af skjult volumen