Endelig element metode - Finite element method
| Differentialligninger |
|---|

|
| Anvendelsesområde |
| Klassifikation |
| Løsning |
| Mennesker |
Den endelige element -metode ( FEM ) er en meget udbredt metode til numerisk løsning af differentialligninger, der opstår inden for teknik og matematisk modellering . Typiske problemområder af interesse omfatter de traditionelle områder af strukturanalyse , varmeoverførsel , væskestrøm , massetransport og elektromagnetisk potentiale .
FEM er en generel numerisk metode til løsning af partielle differentialligninger i to eller tre rumvariabler (dvs. nogle grænseværdiproblemer ). For at løse et problem opdeler FEM et stort system i mindre, enklere dele, der kaldes endelige elementer . Dette opnås ved en særlig rumdiskretisering i rumdimensionerne, som implementeres ved konstruktionen af en maske af objektet: det numeriske domæne for løsningen, som har et begrænset antal punkter. Den endelige elementmetodeformulering af et grænseværdiproblem resulterer endelig i et system med algebraiske ligninger . Metoden tilnærmer den ukendte funktion over domænet. De enkle ligninger, der modellerer disse begrænsede elementer, samles derefter til et større ligningssystem, der modellerer hele problemet. FEM tilnærmer derefter en løsning ved at minimere en tilknyttet fejlfunktion via beregningen af variationer .
At studere eller analysere et fænomen med FEM kaldes ofte endelig elementanalyse ( FEA ).
Basale koncepter
Opdelingen af et helt domæne i enklere dele har flere fordele:
- Nøjagtig repræsentation af kompleks geometri
- Inkludering af forskellige materialegenskaber
- Let repræsentation af totalløsningen
- Optagelse af lokale effekter.
Typisk arbejde ud fra metoden involverer:
- opdeling af problemets domæne i en samling af underdomæner, hvor hvert underdomæne er repræsenteret af et sæt elementligninger til det oprindelige problem
- systematisk rekombination af alle sæt elementligninger til et globalt ligningssystem til den endelige beregning.
Det globale ligningssystem har kendte løsningsteknikker og kan beregnes ud fra de oprindelige værdier for det oprindelige problem for at opnå et numerisk svar.
I det første trin ovenfor er elementligningerne simple ligninger, der lokalt nærmer sig de oprindelige komplekse ligninger, der skal studeres, hvor de originale ligninger ofte er partielle differentialligninger (PDE). For at forklare tilnærmelsen i denne proces introduceres metoden med endelig element normalt som et specielt tilfælde af Galerkin -metoden . Processen, i matematisk sprog, er at konstruere en integral af det indre produkt af rest- og vægtfunktionerne og sætte integralet til nul. Enkelt sagt er det en procedure, der minimerer tilnærmelsesfejlen ved at montere prøvefunktioner i PDE. Resten er fejlen forårsaget af forsøgsfunktionerne, og vægtfunktionerne er polynomiske tilnærmelsesfunktioner, der projicerer residualet. Processen eliminerer alle de rumlige derivater fra PDE'en, hvilket tilnærmer PDE'en lokalt med
- et sæt algebraiske ligninger for steady state -problemer,
- et sæt almindelige differentialligninger for forbigående problemer.
Disse ligningssæt er elementligningerne. De er lineære, hvis den underliggende PDE er lineær og omvendt. Algebraiske ligningssæt, der opstår i steady-state-problemerne, løses ved hjælp af numeriske lineære algebra- metoder, mens almindelige differentialligningssæt , der opstår i de forbigående problemer, løses ved numerisk integration ved hjælp af standardteknikker såsom Eulers metode eller Runge-Kutta- metoden.
I trin (2) ovenfor genereres et globalt ligningssystem fra elementligningerne gennem en transformation af koordinater fra underdomænernes lokale knuder til domænet globale knudepunkter. Denne rumlige transformation omfatter passende orientering justeringer som anvendes i forbindelse med henvisningen koordinatsystem . Processen udføres ofte af FEM -software ved hjælp af koordinatdata genereret fra underdomæner.
FEM forstås bedst fra dens praktiske anvendelse, kendt som finite element analyse (FEA) . FEA som anvendt i teknik er et beregningsværktøj til at udføre ingeniøranalyse . Det inkluderer brug af maskegenereringsteknikker til opdeling af et komplekst problem i små elementer samt brug af software kodet med en FEM -algoritme. Ved anvendelse af FEA er det komplekse problem normalt et fysisk system med den underliggende fysik, såsom Euler-Bernoulli-stråle-ligningen , varme-ligningen eller Navier-Stokes-ligningerne udtrykt i enten PDE eller integrale ligninger , mens de opdelte små elementer i komplekse problem repræsenterer forskellige områder i det fysiske system.
FEA er et godt valg til at analysere problemer over komplicerede domæner (f.eks. Biler og olieledninger), når domænet ændres (som under en solid-state reaktion med en bevægelig grænse), når den ønskede præcision varierer over hele domænet, eller når løsningen mangler glathed. FEA -simuleringer giver en værdifuld ressource, da de fjerner flere tilfælde af oprettelse og test af hårde prototyper til forskellige situationer med høj kvalitet. For eksempel er det i en frontal crash -simulering muligt at øge forudsigelsesnøjagtigheden i "vigtige" områder som bilens forside og reducere den i bagenden (dermed reducere omkostningerne ved simuleringen). Et andet eksempel ville være i numerisk vejrforudsigelse , hvor det er vigtigere at have nøjagtige forudsigelser om udvikling af meget ikke -lineære fænomener (såsom tropiske cykloner i atmosfæren eller hvirvler i havet) frem for relativt rolige områder.
Historie
Selvom det er svært at angive en dato for opfindelsen af metoden med endelig element, stammer metoden fra behovet for at løse komplekse elasticitets- og strukturanalyseproblemer inden for civil- og luftfartsteknik . Dens udvikling kan spores tilbage til værket af A. Hrennikoff og R. Courant i begyndelsen af 1940'erne. En anden pioner var Ioannis Argyris . I Sovjetunionen er introduktionen af den praktiske anvendelse af metoden normalt forbundet med navnet Leonard Oganesyan . Det blev også uafhængigt genopdaget i Kina af Feng Kang i senere 1950'erne og begyndelsen af 1960'erne, baseret på beregninger af dæmningskonstruktioner, hvor det blev kaldt den endelige forskelsmetode baseret på variationsprincip . Selv om den har anvendt, disse pionerer er forskellige, de deler en væsentlig egenskab: mesh diskretisering af en kontinuerlig domæne i et sæt af adskilte subdomæner, normalt betegnet elementer.
Hrennikoff arbejde discretizes domænet ved hjælp af en gitter analogi, mens Courant sin fremgangsmåde opdeler den domæne i finite trekantede underregioner at løse anden ordens elliptiske partielle differentialligninger , der opstår fra problemet med torsion af en cylinder . Courants bidrag var evolutionært og tog udgangspunkt i en lang række tidligere resultater for PDE'er udviklet af Rayleigh , Ritz og Galerkin .
Metoden med begrænset element fik sit virkelige skub i 1960'erne og 1970'erne ved udviklingen af JH Argyris med kolleger ved universitetet i Stuttgart , RW Clough med kolleger ved UC Berkeley , OC Zienkiewicz med kolleger Ernest Hinton , Bruce Irons og andre ved Swansea University , Philippe G. Ciarlet ved University of Paris 6 og Richard Gallagher med kolleger ved Cornell University . Yderligere drivkraft blev givet i disse år af tilgængelige open source -begrænsede elementprogrammer. NASA sponsorerede den originale version af NASTRAN , og UC Berkeley gjorde det endelige elementprogram SAP IV bredt tilgængeligt. I Norge udviklede skibsklassifikationsselskabet Det Norske Veritas (nu DNV GL ) Sesam i 1969 til brug ved analyse af skibe. Et strengt matematisk grundlag for den endelige elementmetode blev leveret i 1973 med udgivelsen af Strang og Fix . Metoden er siden blevet generaliseret til numerisk modellering af fysiske systemer inden for en lang række tekniske discipliner, f.eks. Elektromagnetisme , varmeoverførsel og væskedynamik .
Teknisk diskussion
Strukturen af endelige elementmetoder
En endelig elementmetode er kendetegnet ved en variansformulering , en diskretiseringsstrategi, en eller flere løsningsalgoritmer og procedurer efter behandling.
Eksempler på den variationelle formulering er Galerkin -metoden , den diskontinuerlige Galerkin -metode, blandede metoder osv.
En diskretiseringsstrategi forstås at betyde et klart defineret sæt procedurer, der dækker (a) oprettelse af begrænsede elementmasker, (b) definitionen af basisfunktion på referenceelementer (også kaldet formfunktioner) og (c) kortlægning af reference elementer på elementerne i masken. Eksempler på diskretiseringsstrategier er h-version, p-version , hp-version , x-FEM , isogeometrisk analyse osv. Hver diskretiseringsstrategi har visse fordele og ulemper. Et rimeligt kriterium ved valg af en diskretiseringsstrategi er at realisere næsten optimal ydelse for det bredeste sæt matematiske modeller i en bestemt modelklasse.
Forskellige numeriske løsningsalgoritmer kan inddeles i to brede kategorier; direkte og iterative opløsere. Disse algoritmer er designet til at udnytte den sparsommelighed i matricer, der er afhængige af valgene af variationformulering og diskretiseringsstrategi.
Efterbehandlingsprocedurer er designet til ekstraktion af data af interesse fra en endelig elementløsning. For at opfylde kravene til løsningskontrol skal postprocessorer sørge for et efterfølgende fejlestimat med hensyn til mængderne af interesse. Når tilnærmelsesfejlene er større end det, der anses for acceptabelt, skal diskretiseringen ændres enten ved en automatiseret adaptiv proces eller ved hjælp af analytikeren. Der er nogle meget effektive efterbehandlere, der muliggør realisering af superkonvergens .
Illustrative problemer P1 og P2
Vi vil demonstrere den endelige elementmetode ved hjælp af to prøveproblemer, hvorfra den generelle metode kan ekstrapoleres. Det antages, at læseren kender til beregning og lineær algebra .
P1 er et endimensionelt problem
hvor er givet, er en ukendt funktion af , og er den anden afledte af med hensyn til .
P2 er et todimensionelt problem ( Dirichlet-problem )
hvor er et forbundet åbent område i planet, hvis grænse er pæn (f.eks. en glat manifold eller en polygon ), og og betegner de anden derivater med hensyn til og hhv.
Problemet P1 kan løses direkte ved at beregne antiderivativer . Denne metode til at løse grænseværdiproblemet (BVP) fungerer imidlertid kun, når der er en rumlig dimension og ikke generaliserer til problemer med højere dimension eller problemer som f.eks . Af denne grund vil vi udvikle den endelige elementmetode til P1 og skitsere dens generalisering til P2.
Vores forklaring vil foregå i to trin, som afspejler to væsentlige trin, man skal tage for at løse et grænseværdiproblem (BVP) ved hjælp af FEM.
- I det første trin omformulerer man den originale BVP i sin svage form. Lidt eller ingen beregning er normalt påkrævet for dette trin. Transformationen udføres i hånden på papir.
- Det andet trin er diskretiseringen, hvor den svage form diskretiseres i et endeligt-dimensionelt rum.
Efter dette andet trin har vi konkrete formler til et stort, men endeligt-dimensionelt lineært problem, hvis løsning cirka vil løse det originale BVP. Dette endelig-dimensionelle problem implementeres derefter på en computer .
Svag formulering
Det første trin er at konvertere P1 og P2 til deres ækvivalente svage formuleringer .
Den svage form af P1
Hvis løser P1, så for enhver glat funktion, der opfylder forskydningsgrænsebetingelserne, dvs. ved og , vi har
(1)
Omvendt, hvis med tilfredsstiller (1) for hver glat funktion, kan man vise, at dette vil løse P1. Beviset er lettere for to gange kontinuerligt differentieret ( middelværdisætning ), men kan også bevises i fordelingsforstand .
Vi definerer en ny operatør eller et kort ved at bruge integration af dele på højre side af (1):
(2)
hvor vi har brugt antagelsen om, at .
Den svage form for P2
Hvis vi integrerer med dele ved hjælp af en form for Greens identiteter , ser vi, at hvis løser P2, kan vi definere for enhver ved
hvor betegner gradienten og betegner prikproduktet i det todimensionale plan. Endnu en gang kan omdannes til et indre produkt på et passende rum med engang differentierbare funktioner, der er nul på . Det har vi også antaget (se Sobolev -mellemrum ). Opløsningens eksistens og entydighed kan også vises.
Et bevis på eksistens og løsningens unikke karakter
Vi kan løst tænke på at være de absolut kontinuerlige funktioner, der er på og (se Sobolev -rum ). Sådanne funktioner er (svagt) engang differentierbare, og det viser sig, at det symmetriske to -lineære kort derefter definerer et indre produkt, der bliver til et Hilbert -rum (et detaljeret bevis er ikke -trivialt). På den anden side er venstre side også et indre produkt, denne gang på Lp-rummet . En anvendelse af Riesz -repræsentationsteoremet for Hilbert -mellemrum viser, at der er en unik løsning (2) og derfor P1. Denne løsning er a-priori kun medlem af , men brug af elliptisk regelmæssighed vil være glat, hvis det er.
Diskretisering
P1 og P2 er klar til at blive diskretiseret, hvilket fører til et fælles delproblem (3). Grundtanken er at erstatte det uendeligt-dimensionelle lineære problem:
- Find sådan
med en endelig dimension:
- (3) Find sådan
hvor er et endeligt-dimensionelt underrum af . Der er mange mulige valgmuligheder for (en mulighed fører til spektralmetoden ). For den endelige elementmetode tager vi imidlertid til at være et rum med stykkevis polynomiske funktioner.
For problem P1
Vi tager intervallet , vælger værdier for med og vi definerer ved:
hvor vi definerer og . Bemærk, at funktioner i ikke er differentierbare i henhold til den elementære definition af beregning. Ja, hvis derefter derivatet typisk ikke defineret på noget , . Derivatet eksisterer imidlertid for hver anden værdi af, og man kan bruge dette derivat med henblik på integration af dele .
Til problem P2
Vi skal være et sæt funktioner . I figuren til højre har vi illustreret en triangulering af en 15 -sidet polygonal region i planet (nedenfor) og en stykkevis lineær funktion (ovenfor, i farve) af denne polygon, som er lineær på hver trekant af trianguleringen; rummet ville bestå af funktioner, der er lineære på hver trekant i den valgte triangulering.
Man håber, at efterhånden som det underliggende trekantede net bliver finere og finere, vil løsningen af det diskrete problem (3) på en eller anden måde konvergere til løsningen af det oprindelige grænseværdiproblem P2. For at måle denne maskefinhed indekseres trianguleringen af en parameter med en reel værdi, som man tager for at være meget lille. Denne parameter vil være relateret til størrelsen af den største eller gennemsnitlige trekant i trianguleringen. Når vi forfiner trianguleringen, skal rummet for stykkevis lineære funktioner også ændre sig med . Af denne grund læser man ofte i stedet for i litteraturen. Da vi ikke udfører en sådan analyse, vil vi ikke bruge denne notation.
Valg af grundlag
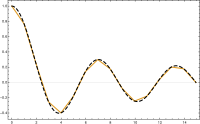
For at fuldføre diskretiseringen skal vi vælge et grundlag for . I det endimensionelle tilfælde vil vi for hvert kontrolpunkt vælge den stykkevis lineære funktion , hvis værdi er på og nul ved hver , dvs.
for ; dette grundlag er en forskudt og skaleret teltfunktion . For det todimensionale tilfælde vælger vi igen en basisfunktion pr. Toppunkt for trianguleringen af det plane område . Funktionen er den unikke funktion, hvis værdi er på og nul for hver .
Afhængigt af forfatteren henviser ordet "element" i "endelig elementmetoden" enten til trekanterne i domænet, den stykkevis lineære basisfunktion eller begge dele. Så for eksempel kan en forfatter, der er interesseret i buede domæner, måske erstatte trekanterne med buede primitiver, og så kunne beskrive elementerne som krumme. På den anden side erstatter nogle forfattere "stykkevis lineær" med "stykkevis kvadratisk" eller endda "stykkevis polynom". Forfatteren kan derefter sige "element af højere orden" i stedet for "højere grad polynom". Den endelige elementmetode er ikke begrænset til trekanter (eller tetraeder i 3-d eller simplexer af højere orden i flerdimensionale rum), men kan defineres på firkantede underdomæner (hexahedra, prismer eller pyramider i 3-d, og så videre) . Højere orden former (krumme linjer) kan defineres med polynomiske og endda ikke-polynomiske former (f.eks. Ellipse eller cirkel).
Eksempler på metoder, der bruger højere grad stykkevis polynomiske basisfunktioner er hp-FEM og spektral FEM .
Mere avancerede implementeringer (adaptive finite element -metoder) anvender en metode til at vurdere kvaliteten af resultaterne (baseret på fejlestimeringsteori) og modificere masken under løsningen med det formål at opnå en omtrentlig løsning inden for nogle grænser fra den nøjagtige løsning af kontinuumproblemet . Mesh -tilpasning kan anvende forskellige teknikker, de mest populære er:
- bevægelige noder (r-adaptivitet)
- raffinering (og uraffinerede) elementer (h-adaptivitet)
- ændring af rækkefølge af basisfunktioner (p-adaptivitet)
- kombinationer af ovenstående ( hp-adaptivitet ).
Lille understøttelse af grundlaget

Den primære fordel ved dette valg af grundlag er, at de indre produkter
og
vil være nul for næsten alle . (Matrixen, der indeholder på stedet, er kendt som Gramian -matricen .) I det endimensionelle tilfælde er understøttelsen af intervallet . Derfor er integranderne af og identisk nul, når som helst .
På samme måde i det plane tilfælde, hvis og ikke deler en kant af trianguleringen, så er integralerne
og
er begge nul.
Matrixform af problemet
Hvis vi skriver og derefter bliver problem (3), tager for , til
- til (4)
Hvis vi betegner med og kolonnen vektorer og , og hvis vi lader
og
være matricer, hvis poster er
og
så kan vi omformulere (4) som
- (5)
Det er ikke nødvendigt at antage . For en generel funktion bliver problem (3) med for faktisk enklere, da ingen matrix bruges,
- , (6)
hvor og til .
Som vi har diskuteret før, er de fleste poster i og nul, fordi basisfunktionerne har lille understøttelse. Så vi er nu nødt til at løse et lineært system i det ukendte, hvor de fleste poster i matricen , som vi skal invertere, er nul.
Sådanne matricer er kendt som sparsomme matricer , og der er effektive opløsere til sådanne problemer (meget mere effektiv end faktisk at vende matrixen.) Desuden er den symmetrisk og positiv bestemt, så en teknik som konjugeret gradientmetode foretrækkes. For problemer, der ikke er for store, fungerer sparsomme LU -nedbrydninger og Cholesky -dekompositioner stadig godt. For eksempel MATLAB kan 's backslash operatør (som bruger sparsomme LU, sparse Cholesky og andre faktoriseringsmetoder) være tilstrækkelig til indgreb med hundredetusinde toppunkter.
Matricen kaldes normalt stivhedsmatricen , mens matrixen kaldes massematricen .
Generel form for finite element metoden
Generelt er metoden med endelig element karakteriseret ved følgende proces.
- Man vælger et gitter til . I den foregående behandling bestod gitteret af trekanter, men man kan også bruge firkanter eller krumme lineære polygoner.
- Derefter vælger man basisfunktioner. I vores diskussion brugte vi stykkevis lineære basisfunktioner, men det er også almindeligt at bruge stykkevis polynomiske basisfunktioner.
Separat hensyn er jævnheden i basisfunktionerne. Ved problemer med anden ordens elliptiske grænseværdier er en polynomisk basisfunktion, der er kontinuert, tilstrækkelig (dvs. derivaterne er diskontinuerlige.) For højere ordens delvise differentialligninger skal man bruge jævnere basisfunktioner. For eksempel kan man for et fjerdeordens problem som f.eks . Bruge stykkevis kvadratiske basisfunktioner .
En anden overvejelse er forholdet mellem det endelige-dimensionelle rum og dets uendelige-dimensionelle modstykke i eksemplerne ovenfor . En konform elementmetode er en metode, hvor rummet er et underrum af elementrummet for det kontinuerlige problem. Eksemplet ovenfor er en sådan metode. Hvis denne betingelse ikke er opfyldt, får vi en ikke -overensstemmende elementmetode , et eksempel på dette er rummet for stykkevis lineære funktioner over netværket, som er kontinuerlige ved hvert kant midtpunkt. Da disse funktioner generelt er diskontinuerlige langs kanterne, er dette endelige-dimensionelle rum ikke et underrum af originalen .
Typisk har man en algoritme til at tage et givet mesh og opdele det. Hvis hovedmetoden til at øge præcisionen er at opdele masken, har man en h -metode ( h er sædvanligvis diameteren på det største element i masken.) Hvis man på denne måde viser, at fejlen med et gitter er afgrænset over af , for nogle og , så har man en ordre p metode. Under visse hypoteser (f.eks. Hvis domænet er konveks), vil et stykkevis polynomisk ordensmetode have en fejl i ordren .
Hvis man i stedet for at gøre h mindre, øger graden af polynomierne, der bruges i basisfunktionen, har man en p -metode. Hvis man kombinerer disse to forfiningstyper, opnår man en hp -metode ( hp -FEM ). I hp-FEM kan polynomgraderne variere fra element til element. Højordensmetoder med stor ensartet p kaldes spectral finite element methods ( SFEM ). Disse må ikke forveksles med spektrale metoder .
For vektorpartielle differentialligninger kan basisfunktionerne tage værdier ind .
Forskellige former for endelige elementmetoder
AEM
Applied Element Method eller AEM kombinerer funktioner i både FEM og Discrete element metode , eller (DEM).
A-FEM
Augmented-Finite Element Method introduceres af Yang og Lui, hvis mål var at modellere de svage og stærke diskontinuiteter uden behov for ekstra DoF'er som i PuM angivet.
Generaliseret finite element metode
Den generaliserede finite element -metode (GFEM) anvender lokale rum bestående af funktioner, ikke nødvendigvis polynomer, der afspejler den tilgængelige information om den ukendte løsning og dermed sikrer en god lokal tilnærmelse. Derefter bruges en opdeling af enhed til at "binde" disse rum sammen for at danne det omtrentlige delrum. Effektiviteten af GFEM er blevet vist, når den anvendes på problemer med domæner med komplicerede grænser, problemer med mikroskalaer og problemer med grænselag.
Blandet endelig elementmetode
Den blandede finite element metode er en type endelig element metode, hvor ekstra uafhængige variabler introduceres som nodale variabler under diskretiseringen af et partielt differentialligningsproblem.
Variabel - polynom
De hp-FEM mejetærskere adaptivt, elementer med variabel størrelse h og polynomium grad p for at opnå usædvanlig hurtig, eksponentielle konvergensprogrammer satser.
hpk-FEM
De Nøjagtig-FEM mejetærskere adaptivt, elementer med variabel størrelse h , polynomiel grad af den lokale tilnærmelser p og global differentiabiliteten af de lokale tilnærmelser (k-1) for at opnå de bedste konvergensprogrammer satser.
XFEM
Den udvidede finite element metode (XFEM) er en numerisk teknik baseret på den generaliserede endelige element metode (GFEM) og partition of unity metoden (PUM). Den udvider den klassiske metode med endelig element ved at berige løsningsrummet for løsninger til differentialligninger med diskontinuerlige funktioner. Udvidede endelige elementmetoder beriger tilnærmelsesrummet, så det naturligt kan gengive det udfordrende træk, der er forbundet med interesseproblemet: diskontinuiteten, singulariteten, grænselaget osv. Det blev vist, at for nogle problemer har en sådan indlejring af problemets funktion i tilnærmelsesrummet kan forbedre konvergenshastigheder og nøjagtighed betydeligt. Desuden undertrykker behandling af problemer med diskontinuiteter med XFEM'er behovet for at maske og ommaske diskontinuitetsoverfladerne og dermed lette beregningsomkostningerne og projektionsfejl forbundet med konventionelle endelige elementmetoder på bekostning af at begrænse diskontinuiteterne til mesh-kanter.
Flere forskningskoder implementerer denne teknik i forskellige grader: 1. GetFEM ++ 2. xfem ++ 3. openxfem ++
XFEM er også blevet implementeret i koder som Altair Radios, ASTER, Morfeo og Abaqus. Det bliver i stigende grad vedtaget af anden kommerciel endelig software, med få plugins og faktiske kerneimplementeringer til rådighed (ANSYS, SAMCEF, OOFELIE osv.).
Scaled boundary finite element method (SBFEM)
Indførelsen af den skalerede grænsebegrænsede elementmetode (SBFEM) kom fra Song and Wolf (1997). SBFEM har været et af de mest rentable bidrag inden for numerisk analyse af brudmekanikproblemer. Det er en semi-analytisk grundlæggende løsningsløs metode, der kombinerer fordelene ved både de endelige elementformuleringer og procedurer og grænselementets diskretisering. I modsætning til grænselementmetoden kræves der imidlertid ingen fundamental differentiel løsning.
S-FEM
S-FEM, Smoothed Finite Element Methods, er en særlig klasse af numeriske simuleringsalgoritmer til simulering af fysiske fænomener. Det blev udviklet ved at kombinere meshfrie metoder med finite element -metoden.
Spektralelementmetode
Spektrale elementmetoder kombinerer den endelige elementers geometriske fleksibilitet og spektrale metoders akutte nøjagtighed. Spektrale metoder er den omtrentlige løsning af svage formdelligninger, der er baseret på højordens Lagrangian-interpolanter og kun bruges med visse kvadraturregler.
Meshfrie metoder
Diskontinuerlige Galerkin -metoder
Endelig elementgrænse analyse
Strakt gittermetode
Loubignac iteration
Loubignac iteration er en iterativ metode i endelige elementmetoder.
Crystal plasticity endelige element metode (CPFEM)
Crystal plasticity finite element method (CPFEM) er et avanceret numerisk værktøj udviklet af Franz Roters. Metaller kan betragtes som krystalaggregater, og de opfører sig anisotropi under deformation, for eksempel unormal stress og belastningslokalisering. CPFEM baseret på slip (forskydningsbelastningshastighed) kan beregne dislokation, krystalorientering og andre teksturoplysninger for at overveje krystalanisotropi under rutinen. Nu er det blevet anvendt i den numeriske undersøgelse af materialedeformation, overfladeruhed, brud og så videre.
Virtuel elementmetode (VEM)
Den virtuelle elementmetode (VEM), introduceret af Beirão da Veiga et al. (2013) som en forlængelse af mimetic finite difference (MFD) metoder, er en generalisering af standard finite element metoden for vilkårlige element geometrier. Dette tillader optagelse af generelle polygoner (eller polyeder i 3D), der er meget uregelmæssige og ikke-konvekse i form. Navnet virtuelt stammer fra det faktum, at viden om det lokale formfunktionsgrundlag ikke er påkrævet og faktisk aldrig er eksplicit beregnet.
Link med gradient diskretiseringsmetoden
Nogle typer af endelige elementmetoder (konform, ikke -konform, blandet finite element metoder) er særlige tilfælde af gradient diskretiseringsmetoden (GDM). Derfor gælder konvergensegenskaberne for GDM, som er etableret for en række problemer (lineære og ikke-lineære elliptiske problemer, lineære, ikke-lineære og degenererede parabolske problemer) også for disse særlige begrænsede elementmetoder.
Sammenligning med metoden med begrænset forskel
Den endelige forskelsmetode (FDM) er en alternativ måde at tilnærme løsninger på PDE'er. Forskellene mellem FEM og FDM er:
- Det mest attraktive træk ved FEM er dens evne til at håndtere komplicerede geometrier (og grænser) relativt let. Mens FDM i sin grundform er begrænset til at håndtere rektangulære former og enkle ændringer deraf, er håndteringen af geometrier i FEM teoretisk ligetil.
- FDM bruges normalt ikke til uregelmæssige CAD -geometrier, men oftere rektangulære eller blokformede modeller.
- Det mest attraktive træk ved begrænsede forskelle er, at det er meget let at implementere.
- Der er flere måder, man kan betragte FDM som et specielt tilfælde af FEM -metoden. F.eks. Er førsteordens FEM identisk med FDM for Poissons ligning , hvis problemet diskretiseres af et almindeligt rektangulært net med hvert rektangel opdelt i to trekanter.
- Der er grunde til at betragte det matematiske grundlag for den endelige tilnærmelse af elementet for eksempel mere sundt, fordi kvaliteten af tilnærmelsen mellem netpunkter er dårlig i FDM.
- Kvaliteten af en FEM-tilnærmelse er ofte højere end i den tilsvarende FDM-tilgang, men dette er ekstremt problemafhængigt, og flere eksempler på det modsatte kan komme.
Generelt er FEM den foretrukne metode til alle former for analyse inden for strukturel mekanik (dvs. løsning for deformation og spændinger i faste legemer eller dynamikker i strukturer), mens beregningsvæskedynamik (CFD) har tendens til at bruge FDM eller andre metoder som metode med begrænset volumen ( FVM). CFD-problemer kræver normalt diskretisering af problemet i et stort antal celler/gridpoints (millioner og mere), derfor fordeler omkostningerne ved løsningen enklere tilnærmelse af lavere orden inden for hver celle. Dette gælder især for problemer med 'eksternt flow', f.eks. Luftstrøm omkring bilen eller flyet eller vejrsimulering.
Ansøgning
En række specialiseringer under paraplyen inden for maskinteknisk disciplin (såsom luftfarts-, biomekanisk og bilindustri) bruger almindeligt integreret FEM i design og udvikling af deres produkter. Flere moderne FEM -pakker indeholder specifikke komponenter såsom termiske, elektromagnetiske, flydende og strukturelle arbejdsmiljøer. I en strukturel simulering hjælper FEM enormt med at producere stivheds- og styrkevisualiseringer og også med at minimere vægt, materialer og omkostninger.
FEM tillader detaljeret visualisering af, hvor strukturer bøjer eller vrider sig, og angiver fordelingen af spændinger og forskydninger. FEM software giver en bred vifte af simuleringsmuligheder til styring af kompleksiteten af både modellering og analyse af et system. På samme måde kan det ønskede nøjagtighedsniveau og tilhørende krav til beregningstid administreres samtidigt for at adressere de fleste tekniske applikationer. FEM tillader, at hele designs konstrueres, forfines og optimeres, før designet fremstilles. Masken er en integreret del af modellen, og den skal kontrolleres omhyggeligt for at give de bedste resultater. Generelt jo højere antal elementer i et net, jo mere præcis er løsningen på det diskretiserede problem. Der er imidlertid en værdi, ved hvilken resultaterne konvergerer, og yderligere netforbedring øger ikke nøjagtigheden.
Dette kraftfulde designværktøj har betydeligt forbedret både standarden for ingeniørdesign og metodikken i designprocessen i mange industrielle applikationer. Indførelsen af FEM har betydeligt reduceret tiden til at tage produkter fra koncept til produktionslinjen. Det er primært gennem forbedrede indledende prototypedesign ved hjælp af FEM, at test og udvikling er blevet fremskyndet. Sammenfattende inkluderer fordelene ved FEM øget nøjagtighed, forbedret design og bedre indsigt i kritiske designparametre, virtuel prototyping, færre hardware -prototyper, en hurtigere og billigere designcyklus, øget produktivitet og øget omsætning.
I 1990'erne blev FEA foreslået til brug i stokastisk modellering til numerisk løsning af sandsynlighedsmodeller og senere til vurdering af pålidelighed.
Se også
- Anvendt elementmetode
- Grænseelementmetode
- Céas lemma
- Computer eksperiment
- Direkte stivhedsmetode
- Diskontinuitetslayoutoptimering
- Diskret element metode
- Endelig forskel metode
- Endelig element maskine
- Endelig element metode i strukturel mekanik
- Endelig volumenmetode
- Endelig volumenmetode til ustabil strømning
- Uendelig element metode
- Interval endeligt element
- Isogeometrisk analyse
- Gitter Boltzmann metoder
- Liste over endelige element softwarepakker
- Meshfrie metoder
- Mobil mobilautomat
- Tværfaglig designoptimering
- Multifysik
- Lappetest
- Rayleigh -Ritz metode
- Rumkortlægning
- Tessellation (computergrafik)
- Svækket svag form
Referencer
Yderligere læsning
- G. Allaire og A. Craig: Numerisk analyse og optimering: En introduktion til matematisk modellering og numerisk simulering .
- KJ Bathe: Numeriske metoder i endelig elementanalyse , Prentice-Hall (1976).
- Thomas JR Hughes: The Finite Element Method: Linear Static and Dynamic Finite Element Analysis, Prentice-Hall (1987).
- J. Chaskalovic: Finite Elements Methods for Engineering Sciences , Springer Verlag, (2008).
- Endre Süli : Endelige elementmetoder til partielle differentialligninger .
- OC Zienkiewicz, RL Taylor, JZ Zhu: The Finite Element Method: Its Basis and Fundamentals , Butterworth-Heinemann (2005).

















































![{\ displaystyle V = \ {v: [0,1] \ rightarrow \ mathbb {R} \ ;: v {\ mbox {er kontinuerlig,}} v | _ {[x_ {k}, x_ {k+1} ]} {\ mbox {er lineær for}} k = 0, \ dots, n {\ mbox {og}} v (0) = v (1) = 0 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d72f354ee5b50866296ad9e758f442f6a32d4b32)









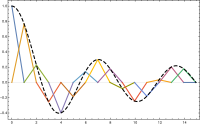




![v_ {k} (x) = \ start {cases} {x-x_ {k-1} \ over x_k \,-x_ {k-1}} & \ mbox {if} x \ i [x_ {k-1 }, x_k], \\ {x_ {k+1} \,-x \ over x_ {k+1} \,-x_k} & \ mbox {if} x \ i [x_k, x_ {k+1}] , \\ 0 & \ mbox {ellers}, \ end {cases}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1d8df33dbf412ea446944402c80c7cab51ecd7e)










![[x_ {k-1}, x_ {k+1}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9ab905e7068db95aeddfd9f0fa55af0e0363843)




































