Kosinuslov - Law of cosines

Fig. 1 - En trekant. Vinklerne

α

(eller

A

),

β

(eller

B

) og

γ

(eller

C

) er henholdsvis modsatte siderne

a

,

b

og

c

.

I trigonometri , den Cosinusrelation (også kendt som cosinus formel , cosinus-reglen , eller al-Kashi 's sætning ) angår længderne af siderne af en trekant til cosinus af en af dens vinkler . Ved hjælp af notation som i fig. 1 angiver cosinusloven

{\ displaystyle c^{2} = a^{2}+b^{2} -2ab \ cos \ gamma,}

hvor $γ$ angiver vinklen mellem siderne af længderne $a$ og $b$ og modsat siden af længden $c$ . For den samme figur er de to andre forhold analoge:

{\ displaystyle a^{2} = b^{2}+c^{2} -2bc \ cos \ alpha,}

{\ displaystyle b^{2} = a^{2}+c^{2} -2ac \ cos \ beta.}

Cosinusloven generaliserer Pythagoras sætning , der kun gælder for rigtige trekanter : hvis vinklen $γ$ er en ret vinkel (måling 90 grader , eller $π$ /2 radianer ), derefter $cos γ = 0$ , og dermed reducerer cosinusloven til Pythagoras sætning :

{\ displaystyle c^{2} = a^{2}+b^{2}.}

Cosinusloven er nyttig til beregning af den tredje side af en trekant, når to sider og deres lukkede vinkel kendes, og til beregning af vinklerne på en trekant, hvis alle tre sider er kendt.

Historie

Fig. 2 - Stump trekant

ABC

med vinkelret

BH

Selvom begrebet den cosinus endnu ikke er udviklet i sin tid, Euclid 's Elements , der går tilbage til det 3. århundrede f.Kr., indeholder en tidlig geometrisk sætning næsten svarer til Cosinusrelation. Tilfældene med stumpe trekanter og akutte trekanter (svarende til de to tilfælde af negativ eller positiv cosinus) behandles separat, i forslag 12 og 13 i bog 2. Trigonometriske funktioner og algebra (især negative tal) er fraværende på Euklides tid, idet udsagn har en mere geometrisk smag:

Proposition 12
I stumpvinklede trekanter er firkanten på den side, der understøtter den stumpe vinkel større end firkanterne på siderne, der indeholder den stumpe vinkel med to gange rektanglet, der er indeholdt af en af siderne om den stumpe vinkel, nemlig den, som vinkelret falder på , og den lige linje afskåret udenfor vinkelret mod den stumpe vinkel.

- Euclids elementer , oversættelse af Thomas L. Heath .

Ved hjælp af notation som i fig. 2 kan Euclids udsagn repræsenteres ved formlen

{\ displaystyle AB^{2} = CA^{2}+CB^{2} +2 (CA) (CH).}

Denne formel kan omdannes til kosinusloven ved at bemærke, at $CH = (CB) cos (π - γ) = - (CB) cos γ$ . Proposition 13 indeholder en helt analog erklæring for akutte trekanter.

Euclids elementer banede vejen for opdagelsen af cosinuslov. I 1400-tallet leverede Jamshīd al-Kāshī , en persisk matematiker og astronom, den første eksplicitte erklæring om kosinusloven i en form, der er egnet til triangulering . Han leverede nøjagtige trigonometriske tabeller og udtrykte sætningen i en form, der er egnet til moderne brug. Fra 1990'erne i Frankrig kaldes cosinusloven stadig Théorème d'Al-Kashi.

Sætningen blev populær i den vestlige verden af François Viète i det 16. århundrede. I begyndelsen af 1800 -tallet tillod moderne algebraisk notation kosinusloven at blive skrevet i sin nuværende symbolske form.

Ansøgninger

Fig. 3 - Anvendelser af kosinusloven: ukendt side og ukendt vinkel.

Sætningen bruges i triangulering til at løse en trekant eller cirkel, dvs. at finde (se figur 3):

den tredje side af en trekant, hvis man kender to sider og vinklen mellem dem:

{\ displaystyle \, c = {\ sqrt {a^{2}+b^{2} -2ab \ cos \ gamma}} \ ,;}

vinklerne på en trekant, hvis man kender de tre sider:

{\ displaystyle \, \ gamma = \ arccos \ left ({\ frac {a^{2}+b^{2} -c^{2}} {2ab}} \ right) \ ,;}

den tredje side af en trekant, hvis man kender to sider og en vinkel modsat en af dem (man kan også bruge Pythagoras sætning til at gøre dette, hvis det er en højre trekant ):

{\ displaystyle \, a = b \ cos \ gamma \ pm {\ sqrt {c^{2} -b^{2} \ sin^{2} \ gamma}} \ ,.}

Disse formler producerer høje afrundingsfejl i flydende punktberegninger, hvis trekanten er meget akut, dvs. hvis $c$ er lille i forhold til $a$ og $b$ eller $γ$ er lille i forhold til 1. Det er endda muligt at opnå et resultat lidt større end en for cosinus af en vinkel.

Den viste tredje formel er resultatet af at løse for a i den kvadratiske ligning $a 2 - 2 ab cos γ + b 2 - c 2 = 0$ . Denne ligning kan have 2, 1 eller 0 positive løsninger svarende til antallet af mulige trekanter givet dataene. Det vil have to positive løsninger, hvis $b sin γ < c < b$ , kun en positiv løsning, hvis $c = b sin γ$ , og ingen løsning, hvis $c < b sin γ$ . Disse forskellige sager forklares også ved tvetydigheden af kongruensens side-side-vinkel .

Beviser

Brug af afstandsformlen

Fig. 4 - Koordinat geometri bevis

Betragt en trekant med sider af længden $a$ , $b$ , $c$ , hvor $θ$ er målingen af vinklen modsat siden af længden $c$ . Denne trekant kan placeres på det kartesiske koordinatsystem med en side $på$ linje langs "x" -aksen og vinklen $θ$ placeret ved oprindelsen ved at tegne komponenterne i trekantens tre punkter som vist i figur 4:

{\ displaystyle A = (b \ cos \ theta, b \ sin \ theta), B = (a, 0), {\ text {og}} C = (0,0).}

Med afstandsformlen ,

{\ displaystyle c = {\ sqrt {(ab \ cos \ theta)^{2}+(0-b \ sin \ theta)^{2}}}.}

Kvadrering på begge sider og forenkling

{\ displaystyle {\ begin {align} c^{2} & {} = (ab \ cos \ theta)^{2}+(-b \ sin \ theta)^{2} \\ c^{2} & {} = a^{2} -2ab \ cos \ theta +b^{2} \ cos^{2} \ theta +b^{2} \ sin^{2} \ theta \\ c^{2} & {} = a^{2} +b^{2} (\ sin^{2} \ theta +\ cos^{2} \ theta) -2ab \ cos \ theta \\ c^{2} & {} = a^{2}+b^{2} -2ab \ cos \ theta. \ end {align}}}

En fordel ved dette bevis er, at det ikke kræver overvejelse af forskellige tilfælde, når trekanten er spids, ret eller stump.

Brug af trigonometri

Fig. 5 - En akut trekant med vinkelret

Fældes vinkelret på siden $c$ gennem punkt $C$ , en højde af trekanten, viser (se fig. 5)

{\ displaystyle c = a \ cos \ beta +b \ cos \ alpha.}

(Dette er stadig sandt, hvis $α$ eller $β$ er stump, i hvilket tilfælde vinkelret falder uden for trekanten.) Multiplicering igennem med $c$ giver

{\ displaystyle c^{2} = ac \ cos \ beta +bc \ cos \ alpha.}

I betragtning af de to andre højder af trekanten giver

{\ displaystyle a^{2} = ac \ cos \ beta +ab \ cos \ gamma,}

{\ displaystyle b^{2} = bc \ cos \ alpha +ab \ cos \ gamma.}

Tilføjelse af de to sidstnævnte ligninger giver

{\ displaystyle a^{2} +b^{2} = ac \ cos \ beta +bc \ cos \ alpha +2ab \ cos \ gamma.}

Hvis man trækker den første ligning fra den sidste, resulterer det i

{\ displaystyle a^{2} +b^{2} -c^{2} = ac \ cos \ beta +bc \ cos \ alpha +2ab \ cos \ gamma -(ac \ cos \ beta +bc \ cos \ alfa)}

hvilket forenkler til

{\ displaystyle c^{2} = a^{2}+b^{2} -2ab \ cos \ gamma.}

Dette bevis anvender trigonometri ved, at det behandler cosinuserne i de forskellige vinkler som mængder i sig selv. Den bruger det faktum, at cosinus af en vinkel udtrykker forholdet mellem de to sider, der omslutter denne vinkel i enhver højre trekant. Andre beviser (nedenfor) er mere geometriske, idet de behandler et udtryk som $et cos γ$ blot som en etiket for længden af et bestemt linjesegment.

Mange beviser omhandler tilfælde af stumpe og spidse vinkler $γ$ separat.

Brug af Pythagoras sætning

Stump trekant

ABC

med højde

BH

Cosinus sætning i plan trigonometri, bevis baseret på Pythagoras sætning.

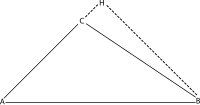
Tilfældet med en stump vinkel

Euklid beviste denne sætning ved at anvende Pythagoras sætning på hver af de to højre trekanter i den viste figur ( $AHB$ og $CHB$ ). Ved at bruge $d$ til at angive linjesegmentet $CH$ og $h$ for højden $BH$ , giver trekant $AHB$ os

{\ displaystyle c^{2} = (b+d)^{2}+h^{2},}

og trekant $CHB$ giver

{\ displaystyle d^{2}+h^{2} = a^{2}.}

Udvidelse af den første ligning giver

{\ displaystyle c^{2} = b^{2}+2bd+d^{2}+h^{2}.}

Ved at erstatte den anden ligning i denne kan følgende opnås:

{\ displaystyle c^{2} = a^{2}+b^{2}+2bd.}

Dette er Euclids forslag 12 fra elementets bog 2 . For at omdanne det til den moderne form for cosinusloven, bemærk det

{\ displaystyle d = a \ cos (\ pi -\ gamma) = -a \ cos \ gamma.}

Tilfælde af en spids vinkel

Euklids bevis på hans forslag 13 foregår i samme retning som hans bevis på forslag 12: han anvender den pythagoranske sætning på begge højre trekanter dannet ved at tabe vinkelret på en af siderne, der omslutter vinklen $γ$ og bruger binomisk sætning til at forenkle.

Fig. 6 - Et kort bevis ved hjælp af trigonometri i tilfælde af en spids vinkel

Endnu et bevis i den akutte sag

Ved hjælp af mere trigonometri kan cosinusloven udledes ved kun at bruge Pythagoras sætning. Faktisk kan det ved hjælp af den højre trekant på venstre side af fig. 6 vises, at: ${\ displaystyle {\ begin {align} \ quad c^{2} & = (ba \ cos \ gamma)^{2}+(a \ sin \ gamma)^{2} \\ & = b^{2} -2ab \ cos \ gamma +a^{2} \ cos^{2} \ gamma +a^{2} \ sin^{2} \ gamma \\ & = b^{2} +a^{2}- 2ab \ cos \ gamma, \ end {align}}}$

ved hjælp af den trigonometriske identitet

${\ displaystyle \ quad \ cos ^{2} \ gamma +\ sin ^{2} \ gamma = 1.}$

Dette bevis kræver en lille ændring, hvis $b < a cos (γ)$ . I dette tilfælde bevæger den højre trekant, som Pythagoras sætning anvendes på, sig uden for trekanten $ABC$ . Den eneste effekt dette har på beregningen er, at mængden $b - a cos (γ)$ erstattes af $en cos (γ) - b .$ Da denne mængde kun indgår i beregningen gennem sin firkant, er resten af beviset upåvirket. Dette problem opstår imidlertid kun, når $β$ er stump, og kan undgås ved at reflektere trekanten omkring bisektor af $γ$ .

Med henvisning til fig. 6 er det værd at bemærke, at hvis vinklen modsat side $a$ er $α$ så:

{\ displaystyle \ tan \ alpha = {\ frac {a \ sin \ gamma} {ba \ cos \ gamma}}.}

Dette er nyttigt til direkte beregning af en anden vinkel, når to sider og en inkluderet vinkel er angivet.

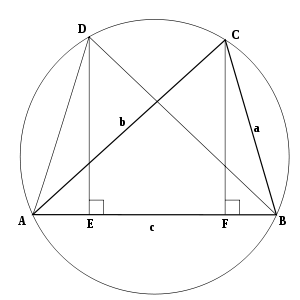
Brug af Ptolemaios 'sætning

Bevis for cosinus lov ved hjælp af Ptolemaios sætning

Med henvisning til diagrammet er trekant ABC med siderne $AB$ = $c$ , $BC$ = $a$ og $AC$ = $b$ tegnet inde i dens cirkel som vist. Trekant $ABD$ er konstrueret kongruent med trekant $ABC$ med $AD$ = $BC$ og $BD$ = $AC$ . Perpendikulærerne fra $D$ og $C$ mødes basen $AB$ på $E$ og $F$ henholdsvis. Derefter:

{\ displaystyle {\ begin {align} & BF = AE = BC \ cos {\ hat {B}} = a \ cos {\ hat {B}} \\\ Højre pil \ & DC = EF = AB-2BF = c-2a \ cos {\ hat {B}}. \ end {align}}}

Nu er cosinusloven gengivet ved en ligetil anvendelse af Ptolemaios 'teorem til cyklisk firkant $ABCD$ :

{\ displaystyle {\ begin {align} & AD \ times BC+AB \ times DC = AC \ times BD \\\ Rightarrow \ & a^{2}+c (c-2a \ cos {\ hat {B}}) = b^{2} \\\ Højre pil \ & a^{2}+c^{2} -2ac \ cos {\ hat {B}} = b^{2}. \ end {align}}}

Hvis vinkel $B$ er rigtigt , er $ABCD$ et rektangel, og anvendelse af Ptolemaios sætning giver Pythagoras sætning :

{\ displaystyle a^{2}+c^{2} = b^{2}. \ quad}

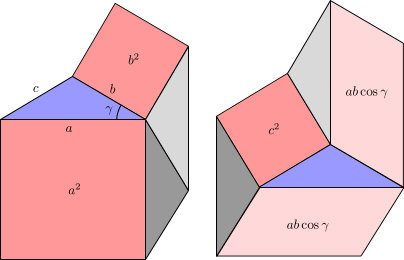
Ved at sammenligne områder

Man kan også bevise cosinusloven ved at beregne områder . Ændringen af tegnet, efterhånden som vinklen $γ$ bliver stump, gør en sagssondring nødvendig.

Husk det

$a 2$ , $b 2$ og $c 2$ er arealerne på firkanterne med siderne henholdsvis $a$ , $b$ og $c$ ;
hvis $γ$ er akut, så er $ab cos γ$ arealet af parallelogrammet med siderne $a$ og $b, der$ danner en vinkel på $γ ' = π / 2 - y$ ;
hvis $γ$ er stump, og så $cos γ$ er negativ, så $- ab cos γ$ er arealet af parallelogrammet med siderne a og b, der danner en vinkel på $γ ' = γ - π / 2$ .

Fig. 7a - Bevis for cosinusloven for spids vinkel

γ

ved "klipning og indsætning".

Akut sag. Figur 7a viser en heptagon skåret i mindre stykker (på to forskellige måder) for at give et bevis på cosinusloven. De forskellige stykker er

i pink, områderne $a 2$ , $b 2$ til venstre og områderne $2 ab cos γ$ og $c 2$ til højre;
i blå, trekanten $ABC$ , til venstre og til højre;
i grå, hjælpetrekanter, alle kongruente med $ABC$ , et lige antal (nemlig 2) både til venstre og til højre.

Ligheden mellem områder til venstre og til højre giver

{\ displaystyle \, a^{2}+b^{2} = c^{2}+2ab \ cos \ gamma \ ,.}

Fig. 7b - Bevis for cosinusloven for stump vinkel

γ

ved "klipning og indsætning".

Stump sag. Figur 7b skærer en sekskant på to forskellige måder i mindre stykker, hvilket giver et bevis på cosinusloven i tilfælde af at vinklen $γ$ er stump. Vi har

i pink, områderne $a 2$ , $b 2$ og $-2 ab cos γ$ til venstre og $c 2$ til højre;
i blå, trekanten $ABC$ to gange, til venstre såvel som til højre.

Ligheden mellem områder til venstre og til højre giver

{\ displaystyle \, a^{2}+b^{2} -2ab \ cos (\ gamma) = c^{2}.}

Det strenge bevis skal indeholde beviser for, at forskellige former er kongruente og derfor har samme areal. Dette vil bruge teorien om kongruente trekanter .

Brug af cirkelens geometri

Ved hjælp af cirkelens geometri er det muligt at give et mere geometrisk bevis end at bruge Pythagoras sætning alene. Algebraiske manipulationer (især binomisk sætning ) undgås.

Fig. 8a - Trekanten

ABC

(pink), en hjælpecirkel (lyseblå) og en ekstra trekant (gul)

Tilfælde af spids vinkel $γ$ , hvor $a > 2 b cos γ$ . Drop vinkelret fra $A$ på $a$ = $BC$ , hvilket skaber et linjesegment med længde $b cos γ$ . Dupliker den højre trekant for at danne den ensartede trekant $ACP$ . Konstruere cirkel med centrum $A$ og radius $b$ , og dens tangent $h = BH$ gennem $B$ . Tangenten $h$ danner en ret vinkel med radius $b$ (Euklides elementer : Bog 3, proposition 18; eller se her ), så den gule trekant i figur 8 er rigtig. Anvend Pythagoras sætning for at opnå

{\ displaystyle c^{2} = b^{2}+h^{2}.}

Brug derefter tangent -sekant -sætningen (Euklids elementer : Bog 3, forslag 36), der siger, at firkanten på tangenten gennem et punkt $B$ uden for cirklen er lig med produktet af de to linjesegmenter (fra $B$ ), der er skabt af enhver sekant af cirklen gennem $B$ . I det foreliggende tilfælde: $BH 2 = BC \cdot BP$ , eller

{\ displaystyle h^{2} = a (a-2b \ cos \ gamma).}

Ved at erstatte den tidligere ligning får man cosinusloven:

{\ displaystyle c^{2} = b^{2}+a (a-2b \ cos \ gamma).}

Bemærk, at $h 2$ er kraften i punktet $B$ i forhold til cirklen. Anvendelsen af Pythagoras sætning og tangentsekant sætning kan erstattes af en enkelt anvendelse af en punkts sætnings kraft .

Fig. 8b - Trekanten

ABC

(pink), en hjælpecirkel (lyseblå) og to ekstra højre trekanter (gul)

Tilfælde af spids vinkel $γ$ , hvor $a <2 b cos γ$ . Drop vinkelret fra $A$ på $a$ = $BC$ , hvilket skaber et linjesegment med længde $b cos γ$ . Dupliker den højre trekant for at danne den ensartede trekant $ACP$ . Konstruer cirklen med centrum $A$ og radius $b$ , og en akkord gennem $B$ vinkelret på $c = AB, hvoraf$ halvdelen er $h = BH .$ Anvend Pythagoras sætning for at opnå

{\ displaystyle b^{2} = c^{2}+h^{2}.}

Brug nu akkordsætningen (Euclids elementer : Bog 3, forslag 35), der siger, at hvis to akkorder skærer hinanden, er produktet af de to linjesegmenter opnået på den ene akkord lig med produktet af de to linjesegmenter opnået på den anden akkord . I det foreliggende tilfælde: $BH 2 = BC \cdot BP,$ eller

{\ displaystyle h^{2} = a (2b \ cos \ gamma -a).}

Ved at erstatte den tidligere ligning får man cosinusloven:

{\ displaystyle b^{2} = c^{2}+a (2b \ cos \ gamma -a) \ ,.}

Bemærk, at punktets effekt $B$ i forhold til cirklen har den negative værdi $- h 2$ .

Fig. 9 - Bevis for cosinusloven ved hjælp af en punkts sætning.

Tilfælde af stump vinkel $γ$ . Dette bevis anvender kraften i en punktsætning direkte uden hjælpetrekanter opnået ved at konstruere en tangent eller en akkord. Konstruere en cirkel med centrum $B$ og radius $a$ (se figur 9), som skærer sekant gennem $A$ og $C$ i $C$ og $K$ . Den magt af punktet $A$ i forhold til cirklen er lig med både $AB 2 - BC 2$ og $AC \cdot AK$ . Derfor,

{\ displaystyle {\ begin {align} c^{2} -a^{2} & {} = b (b+2a \ cos (\ pi-\ gamma)) \\ & {} = b (b-2a \ cos \ gamma), \ end {align}}}

som er kosinusloven.

Ved brug af algebraiske mål for linjesegmenter (der tillader negative tal som længder af segmenter) kan stump vinkel ( $CK > 0$ ) og spids vinkel ( $CK <0$ ) behandles samtidigt.

Brug af syndens lov

Ved at bruge syndeloven og vide, at vinklerne på en trekant skal summe til 180 grader, har vi følgende ligningssystem (de tre ukendte er vinklerne):

{\ displaystyle {\ frac {c} {\ sin \ gamma}} = {\ frac {b} {\ sin \ beta}},}

{\ displaystyle {\ frac {c} {\ sin \ gamma}} = {\ frac {a} {\ sin \ alpha}},}

{\ displaystyle \ alpha +\ beta +\ gamma = \ pi.}

Derefter opnår vi ved hjælp af systemets tredje ligning et system med to ligninger i to variabler:

{\ displaystyle {\ frac {c} {\ sin \ gamma}} = {\ frac {b} {\ sin (\ alpha +\ gamma)}},}

{\ displaystyle {\ frac {c} {\ sin \ gamma}} = {\ frac {a} {\ sin \ alpha}},}

hvor vi har brugt den trigonometriske egenskab, at sinus for en supplerende vinkel er lig med vinklen sinus.

Brug af identiteten (se vinkelsum og differensidentiteter )

{\ displaystyle \ sin (\ alpha +\ gamma) = \ sin \ alpha \ cos \ gamma +\ sin \ gamma \ cos \ alpha}

fører til

{\ displaystyle c (\ sin \ alpha \ cos \ gamma +\ sin \ gamma \ cos \ alpha) = b \ sin \ gamma,}

{\ displaystyle c \ sin \ alpha = a \ sin \ gamma.}

Ved at dividere hele systemet med $cos γ$ har vi:

{\ displaystyle c (\ sin \ alpha +\ tan \ gamma \ cos \ alpha) = b \ tan \ gamma,}

{\ displaystyle {\ frac {c \ sin \ alpha} {\ cos \ gamma}} = a \ tan \ gamma,}

{\ displaystyle {\ frac {c ^{2} \ sin ^{2} \ alpha} {\ cos ^{2} \ gamma}} = a ^{2} \ tan ^{2} \ gamma.}

Derfor kan vi opnå fra den første ligning af systemet

{\ displaystyle {\ frac {c \ sin \ alpha} {bc \ cos \ alpha}} = \ tan \ gamma}

Ved at erstatte dette udtryk i den anden ligning og ved at bruge

{\ displaystyle 1+ \ tan ^{2} \ gamma = {\ frac {1} {\ cos ^{2} \ gamma}}}

vi kan få en ligning med en variabel:

{\ displaystyle c^{2} \ sin^{2} \ alpha \ left [1+{\ frac {c^{2} \ sin^{2} \ alpha} {(bc \ cos \ alpha)^{2 }}} \ right] = a^{2} \ cdot {\ frac {c^{2} \ sin^{2} \ alpha} {(bc \ cos \ alpha)^{2}}}}

Ved at gange med $(b - c cos α) 2$ kan vi opnå følgende ligning:

{\ displaystyle (bc \ cos \ alpha)^{2}+c^{2} \ sin^{2} \ alpha = a^{2}.}

Dette indebærer

{\ displaystyle b^{2} -2bc \ cos \ alpha +c^{2} \ cos^{2} \ alpha +c^{2} \ sin^{2} \ alpha = a^{2}.}

Når vi husker den pythagoranske identitet , får vi kosinusloven:

{\ displaystyle a^{2} = b^{2}+c^{2} -2bc \ cos \ alpha.}

Brug af vektorer

Betegn

{\ displaystyle {\ overrightarrow {CB}} = {\ vec {a}}, \ {\ overrightarrow {CA}} = {\ vec {b}}, \ {\ overrightarrow {AB}} = {\ vec {c }}}

Derfor,

{\ displaystyle {\ vec {c}} = {\ vec {a}}-{\ vec {b}}}

At tage prikproduktet på hver side med sig selv:

{\ displaystyle {\ vec {c}} \ cdot {\ vec {c}} = ({\ vec {a}}-{\ vec {b}}) \ cdot ({\ vec {a}}-{\ vec {b}})}

{\ displaystyle \ Vert {\ vec {c}} \ Vert ^{2} = \ Vert {\ vec {a}} \ Vert ^{2}+\ Vert {\ vec {b}} \ Vert ^{2} -2 \, {\ vec {a}} \ cdot {\ vec {b}}}

Brug af identiteten (se Dot -produkt )

{\ displaystyle {\ vec {u}} \ cdot {\ vec {v}} = \ Vert {\ vec {u}} \ Vert \, \ Vert {\ vec {v}} \ Vert \ cos \ vinkel ({ \ vec {u}}, \ {\ vec {v}})}

fører til

{\ displaystyle \ Vert {\ vec {c}} \ Vert ^{2} = \ Vert {\ vec {a}} \ Vert ^{2}+{\ Vert {\ vec {b}} \ Vert} ^{ 2} -2 \, \ Vert {\ vec {a}} \ Vert \! \; \ Vert {\ vec {b}} \ Vert \ cos \ vinkel ({\ vec {a}}, \ {\ vec { b}})}

Resultatet følger.

Ensartet kasse

Når $a = b$ , dvs. når trekanten er ensartet med de to sider, der falder ind i vinklen $γ$ lige, forenkler cosinusloven betydeligt. Nemlig fordi $a 2 + b 2 = 2 a 2 = 2 ab$ , bliver kosinusloven

{\ displaystyle \ cos \ gamma = 1-{\ frac {c^{2}} {2a^{2}}}}

eller

{\ displaystyle c^{2} = 2a^{2} (1- \ cos \ gamma).}

Analog for tetraeder

En analog sætning begynder med at tage $α$ , $β$ , $γ$ , $δ for$ at være arealerne på de fire flader af et tetraeder . Betegn de dihedrale vinkler med osv. Så ${\ displaystyle {\ widehat {\ beta \ gamma}}}$

{\ displaystyle \ alpha ^{2} = \ beta ^{2}+\ gamma ^{2}+\ delta ^{2} -2 \ venstre [\ beta \ gamma \ cos \ left ({\ widehat {\ beta \ gamma}} \ right)+\ gamma \ delta \ cos \ left ({\ widehat {\ gamma \ delta}} \ right)+\ delta \ beta \ cos \ left ({\ widehat {\ delta \ beta}} \ højre) \ højre].}

Version egnet til små vinkler

Når vinklen, $γ$ , er lille, og de tilstødende sider, $a$ og $b$ , har samme længde, kan højre side af cosinuslovens standardform miste meget nøjagtighed til numerisk tab af betydning . I situationer, hvor dette er en vigtig bekymring, kan en matematisk ækvivalent version af cosinusloven , der ligner haversinformlen , vise sig nyttig:

{\ displaystyle {\ begin {align} c^{2} & = (ab)^{2}+4ab \ sin^{2} \ venstre ({\ frac {\ gamma} {2}} \ right) \\ & = (ab)^{2}+4ab \ operatorname {haversin} (\ gamma). \ end {align}}}

I grænsen for en uendelig vinkel degenererer cosinusloven til formlen med cirkelbue , $c = a γ$ .

I sfærisk og hyperbolsk geometri

Sfærisk trekant løst ved kosinusloven.

Versioner, der ligner cosinusloven for det euklidiske plan, holder også på en enhedsfære og i et hyperbolsk plan. I sfærisk geometri er en trekant defineret af tre punkter $u$ , $v$ og $w$ på enhedssfæren, og buerne i store cirkler, der forbinder disse punkter. Hvis disse store cirkler danner vinkler $A$ , $B$ og $C$ med modsatte sider $a$ , $b$ , $c,$ så hævder cosinus sfæriske lov , at begge følgende forhold holder:

{\ displaystyle {\ begin {align} \ cos a & = \ cos b \ cos c+\ sin b \ sin c \ cos A \\\ cos A & =-\ cos B \ cos C+\ sin B \ sin C \ cos a . \ end {align}}}

I hyperbolsk geometri er et par ligninger i fællesskab kendt som cosinus hyperboliske lov . Det første er

{\ displaystyle \ cosh a = \ cosh b \ cosh c- \ sinh b \ sinh c \ cos A}

hvor $sinh$ og $cosh$ er den hyperboliske sinus og cosinus , og den anden er

{\ displaystyle \ cos A =-\ cos B \ cos C+\ sin B \ sin C \ cosh a.}

Som i euklidisk geometri kan man bruge kosinusloven til at bestemme vinklerne $A$ , $B$ , $C ud$ fra kendskabet til siderne $a$ , $b$ , $c$ . I modsætning til den euklidiske geometri er det omvendte også muligt i begge ikke-euklidiske modeller: vinklerne $A$ , $B$ , $C$ bestemmer siderne $a$ , $b$ , $c$ .

Ensartet formel til overflader med konstant krumning

Definere to funktioner og som ${\ displaystyle \ cos _ {R}}$ ${\ displaystyle \ sin _ {R}}$

{\ displaystyle \ cos _ {R} (x) = \ cos (x/R) \ quad}

og

{\ displaystyle \ quad \ sin _ {R} (x) = R \ cdot \ sin (x/R)}

gør det muligt at forene formlerne for fly , kugle og pseudosfære til:

{\ displaystyle \ cos _ {R} (BC) = \ cos _ {R} (AB) \ cdot \ cos _ {R} (AC)+{\ frac {1} {R^{2}}} \ sin _ {R} (AB) \ cdot \ sin _ {R} (AC) \ cdot \ cos ({\ widehat {BAC}}).}

I denne notation er et komplekst tal , der repræsenterer overfladens krumningsradius . ${\ displaystyle R}$

For overfladen er en sfære med radius , og dens konstante krumning er lig ${\ displaystyle R \ in \ mathbb {R}}$ ${\ displaystyle R}$ ${\ displaystyle 1/R^{2};}$

for overfladen er en pseudosfære med (imaginær) radius med konstant krumning lig med ${\ displaystyle R = iR '\ colon R' \ in \ mathbb {R}}$ ${\ displaystyle R,}$ ${\ displaystyle 1/R^{2} =-1/R '^{2};}$

for : overfladen har tendens til et euklidisk plan , med konstant nul -krumning. ${\ displaystyle R \ to \ infty}$

Bekræftelse af formlen for ikke-euklidisk geometri

I de to første tilfælde og er veldefinerede over hele det komplekse plan for alle , og at hente tidligere resultater er ligetil. ${\ displaystyle \ cos _ {R}}$ ${\ displaystyle \ sin _ {R}}$ ${\ displaystyle R \ neq 0}$