Ikke-ensartet rationel B-spline- Non-uniform rational B-spline

En NURBS -kurve. (Se også: den animerede oprettelse af en NURBS -spline .)

En NURBS overflade

Ikke-ensartet rationel basis spline ( NURBS ) er en matematisk model, der bruger basis splines (B-splines), der almindeligvis bruges i computergrafik til at repræsentere kurver og overflader . Det giver stor fleksibilitet og præcision til håndtering af både analytiske (defineret ved almindelige matematiske formler ) og modellerede former . Det er en form for kurvemodellering , i modsætning til polygonal modellering eller digital skulptur . NURBS-kurver bruges almindeligvis i computerstøttet design (CAD), fremstilling (CAM) og teknik (CAE). De er en del af talrige branchedækkende standarder, såsom IGES , STEP , ACIS og PHIGS . Værktøjer til oprettelse og redigering af NURBS -overflader findes i forskellige 3D -grafik- og animationssoftwarepakker .

De kan håndteres effektivt af computerprogrammer, men muliggør let menneskelig interaktion. NURBS overflader er funktioner af to parametre, der kortlægger til en overflade i tredimensionelt rum . Overfladens form bestemmes af kontrolpunkter . I en kompakt form kan NURBS -overflader repræsentere enkle geometriske former . For komplekse organiske former er T-splines og underopdelingsoverflader mere egnede, fordi de halverer antallet af kontrolpunkter i sammenligning med NURBS-overfladerne.

Generelt er redigering af NURBS kurver og overflader intuitiv og forudsigelig. Kontrolpunkter er altid enten forbundet direkte til kurven eller overfladen, eller fungerer som om de var forbundet med et gummibånd. Afhængigt af typen af brugergrænseflade kan redigeringen af NURBS -kurver og overflader ske via deres kontrolpunkter (ligner Bézier -kurver ) eller via værktøjer på højere niveau, såsom spline -modellering og hierarkisk redigering .

Historisk baggrund

En flad spline , en fysisk manifestation af spline som et matematisk begreb

Før computere blev designs tegnet i hånden på papir med forskellige redigeringsværktøjer . Linealer blev brugt til lige linjer, kompasser til cirkler og vinkelmålinger . Men mange former, f.eks. Friformskurven for et skibs bue, kunne ikke tegnes med disse værktøjer. Selvom sådanne kurver kunne trækkes frihånd på tegnebrættet, havde skibsbyggere ofte brug for en version i naturlig størrelse, som ikke kunne udføres i hånden. Sådanne store tegninger blev udført ved hjælp af fleksible træstrimler, kaldet splines. Splines blev holdt på plads på et antal forudbestemte punkter, kaldet "ænder"; mellem ænderne fik splinematerialets elasticitet stripen til at tage den form, der minimerede bøjningsenergien og dermed skabe den mest jævne form, der passer til begrænsningerne. Formen kunne justeres ved at flytte ænderne.

I 1946 begyndte matematikere at studere spline -formen og udledte den stykkevise polynomformel kendt som spline -kurven eller spline -funktionen. IJ Schoenberg gav spline -funktionen sit navn efter sin lighed med den mekaniske spline, der blev brugt af tegnere.

Da computere blev introduceret i designprocessen, blev de fysiske egenskaber ved sådanne splines undersøgt, så de kunne modelleres med matematisk præcision og gengives, hvor det er nødvendigt. Banebrydende arbejde blev udført i Frankrig af Renault -ingeniøren Pierre Bézier og Citroëns fysiker og matematiker Paul de Casteljau . De arbejdede næsten parallelt med hinanden, men fordi Bézier offentliggjorde resultaterne af sit arbejde, blev Bézier -kurver opkaldt efter ham, mens de Casteljaus navn kun er forbundet med relaterede algoritmer.

I første omgang blev NURBS kun brugt i proprietære CAD -pakker fra bilfirmaer. Senere blev de en del af standard computergrafikpakker.

Real-time, interaktiv gengivelse af NURBS-kurver og -overflader blev første gang gjort kommercielt tilgængelig på Silicon Graphics- arbejdsstationer i 1989. I 1993 blev den første interaktive NURBS-model til pc'er, kaldet NöRBS, udviklet af CAS Berlin, et lille startfirma, der samarbejder med Berlins tekniske universitet .

Kontinuitet

En overflade under opførelse, f.eks. Skroget på en motoryacht, består normalt af flere NURBS -overflader kendt som patches . Disse plaster skal monteres på en sådan måde, at grænserne er usynlige. Dette udtrykkes matematisk ved begrebet geometrisk kontinuitet .

Der findes værktøjer på højere niveau, der drager fordel af NURBS 'evne til at skabe og etablere geometrisk kontinuitet på forskellige niveauer:

Positionskontinuitet (G ⁰ ) holder, når slutpositionerne på to kurver eller overflader falder sammen. Kurverne eller overfladerne kan stadig mødes i en vinkel, hvilket giver anledning til et skarpt hjørne eller en kant og forårsager ødelagte højdepunkter.
Tangential kontinuitet (G¹) kræver, at endevektorerne på kurverne eller overfladerne er parallelle og peger på samme måde og udelukker skarpe kanter. Fordi højdepunkter, der falder på en tangentielt kontinuerlig kant, altid er kontinuerlige og dermed ser naturlige ud, kan dette niveau af kontinuitet ofte være tilstrækkeligt.
Krumningskontinuitet (G²) kræver endvidere, at endevektorerne har samme længde og ændring i længden. Højdepunkter, der falder på en krumningskontinuerlig kant, viser ingen ændringer, hvilket får de to overflader til at fremstå som en. Dette kan visuelt genkendes som "helt glat". Dette niveau af kontinuitet er meget nyttigt i skabelsen af modeller, der kræver mange bi-kubiske patches, der danner en kontinuerlig overflade.

Geometrisk kontinuitet refererer hovedsageligt til formen af den resulterende overflade; da NURBS -overflader er funktioner, er det også muligt at diskutere overfladerivaterne med hensyn til parametrene. Dette er kendt som parametrisk kontinuitet . Parametrisk kontinuitet af en given grad indebærer geometrisk kontinuitet af denne grad.

Første og andet niveau parametrisk kontinuitet (C ⁰ og C¹) er af praktiske formål identiske med positionel og tangential (G ⁰ og G¹) kontinuitet. Tredje niveau parametrisk kontinuitet (C²) adskiller sig imidlertid fra krumningskontinuitet ved at parameteriseringen også er kontinuerlig. I praksis er C²-kontinuitet lettere at opnå, hvis der bruges ensartede B-splines.

Definitionen af C ⁿ -kontinuitet kræver, at n -derivatet af tilstødende kurver/overflader ( ) er ens ved en samling. Bemærk, at (del) derivater af kurver og overflader er vektorer, der har en retning og en størrelse; begge skal være lige. ${\ displaystyle d^{n} C (u)/du^{n}}$

Højdepunkter og refleksioner kan afsløre den perfekte udjævning, som ellers er praktisk talt umulig at opnå uden NURBS -overflader, der har mindst G² -kontinuitet. Det samme princip bruges som en af overfladeevalueringsmetoderne, hvorved et strålesporet eller refleksionskortet billede af en overflade med hvide striber, der reflekterer på den, vil vise selv de mindste afvigelser på en overflade eller et sæt overflader. Denne metode stammer fra bilprototyper, hvor overfladekvalitet inspiceres ved at kontrollere kvaliteten af reflekser af et neonlysloft på bilens overflade. Denne metode er også kendt som "Zebra -analyse".

Tekniske specifikationer

En NURBS -kurve er defineret af dens rækkefølge, et sæt vægtede kontrolpunkter og en knudevektor. NURBS kurver og overflader er generaliseringer af både B-splines og Bézier kurver og overflader, den primære forskel er vægtningen af kontrolpunkterne, hvilket gør NURBS-kurver rationelle . ( Ikke-rationelle , alias simple , B-splines er et specielt tilfælde/delsæt af rationelle B-splines, hvor hvert kontrolpunkt er en regelmæssig ikke-homogen koordinat [nej 'w'] frem for en homogen koordinat . Det svarer til har vægt "1" ved hvert kontrolpunkt; Rationelle B-splines bruger 'w' for hvert kontrolpunkt som en vægt .) Ved at bruge et todimensionalt gitter af kontrolpunkter kan NURBS-overflader inklusive plane patches og sektioner af kugler oprettet. Disse parametriseres med to variabler (typisk kaldet s og t eller u og v ). Dette kan udvides til vilkårlige dimensioner for at oprette NURBS -kortlægning . ${\ displaystyle \ mathbb {R} ^{n} \ to \ mathbb {R} ^{n}}$

NURBS kurver og overflader er nyttige af en række årsager:

Sættet med NURBS for en given ordre er invariant under affine transformationer: operationer som rotationer og translationer kan anvendes på NURBS kurver og overflader ved at anvende dem på deres kontrolpunkter.
De tilbyder en fælles matematisk form for både standard analytiske former (f.eks. Kegler ) og former i fri form.
De giver fleksibiliteten til at designe en lang række former.
De reducerer hukommelsesforbruget ved lagring af figurer (sammenlignet med enklere metoder).
De kan evalueres rimeligt hurtigt ved hjælp af numerisk stabile og præcise algoritmer .

Her diskuteres NURBS mest i en dimension (kurver); det kan generaliseres til to (overflader) eller endnu flere dimensioner.

Bestille

Den rækkefølge af en NURBS kurve definerer antallet af nærliggende kontrolpunkter, der påvirker et givent punkt på kurven. Kurven repræsenteres matematisk af et polynom med en grad mindre end kurvens rækkefølge. Derfor kaldes andenordens kurver (som er repræsenteret ved lineære polynomier) lineære kurver, tredje orden kurver kaldes kvadratiske kurver, og fjerde ordens kurver kaldes kubiske kurver. Antallet af kontrolpunkter skal være større end eller lig kurvens rækkefølge.

I praksis er kubikkurver dem, der oftest bruges. Femte og sjette ordens kurver er undertiden nyttige, især for at opnå kontinuerlige højere ordens derivater, men kurver for højere ordrer bruges praktisk talt aldrig, fordi de fører til interne numeriske problemer og har en tendens til at kræve uforholdsmæssigt store beregningstider.

Kontrolpunkter

Tredimensionelle NURBS-overflader kan have komplekse, organiske former. Kontrolpunkter påvirker de retninger, overfladen tager. En separat firkant under kontrolburet afgrænser X- og Y -overfladen af overfladen.

Kontrolpunkterne bestemmer kurvens form. Typisk beregnes hvert punkt i kurven ved at tage en vægtet sum af et antal kontrolpunkter. Vægten af hvert punkt varierer afhængigt af den styrende parameter. For en kurve med grad d er vægten af et vilkårligt kontrolpunkt kun nul i d+1 intervaller af parameterrummet. Inden for disse intervaller ændres vægten i henhold til en polynomfunktion ( basisfunktioner ) af grad d. Ved intervallernes grænser går basisfunktionerne jævnt til nul, glatheden bestemmes af polynomets grad.

Som et eksempel er basisfunktionen i grad 1 en trekantfunktion. Den stiger fra nul til en og falder derefter til nul igen. Mens den stiger, falder grundfunktionen for det tidligere kontrolpunkt. På den måde interpolerer kurven mellem de to punkter, og den resulterende kurve er en polygon, som er kontinuerlig , men ikke differentierbar ved intervalgrænserne eller knuder. Polynom i højere grad har tilsvarende mere kontinuerlige derivater. Bemærk, at inden for intervallet gør basisfunktionernes polynomiske karakter og konstruktionens linearitet kurven helt glat, så det er kun ved knuderne, at diskontinuitet kan opstå.

I mange applikationer er det en meget ønskelig egenskab, kendt som lokal support , at et enkelt kontrolpunkt kun påvirker de intervaller, hvor det er aktivt . I modellering tillader det ændring af en del af en overflade, mens andre dele forbliver uændrede.

Tilføjelse af flere kontrolpunkter tillader bedre tilnærmelse til en given kurve, selvom kun en bestemt kurveklasse kan repræsenteres nøjagtigt med et begrænset antal kontrolpunkter. NURBS kurver har også en skalar vægt for hvert kontrolpunkt. Dette giver mulighed for mere kontrol over kurvens form uden unødigt at øge antallet af kontrolpunkter. Især tilføjer det keglesnit som cirkler og ellipser til det sæt kurver, der kan repræsenteres nøjagtigt. Udtrykket rationelt i NURBS refererer til disse vægte.

Kontrolpunkterne kan have enhver dimension . Endimensionelle punkter definerer bare en skalarfunktion af parameteren. Disse bruges typisk i billedbehandlingsprogrammer til at justere lysstyrken og farvekurverne. Tredimensionelle kontrolpunkter bruges rigeligt i 3D-modellering, hvor de bruges i den daglige betydning af ordet 'punkt', en placering i 3D-rum. Multidimensionelle punkter kan bruges til at styre sæt af tidsdrevne værdier, f.eks. De forskellige positions- og rotationsindstillinger for en robotarm. NURBS overflader er kun en anvendelse af dette. Hvert kontrol 'punkt' er faktisk en fuld vektor af kontrolpunkter, der definerer en kurve. Disse kurver deler deres grad og antallet af kontrolpunkter og spænder over en dimension af parameterrummet. Ved at interpolere disse kontrolvektorer over den anden dimension af parameterrummet opnås et kontinuerligt sæt kurver, der definerer overfladen.

Knude vektor

Knudevektoren er en sekvens af parameterværdier, der bestemmer, hvor og hvordan kontrolpunkterne påvirker NURBS -kurven. Antallet af knuder er altid lig med antallet af kontrolpunkter plus kurvegrad plus en (dvs. antal kontrolpunkter plus kurverækkefølge). Knudevektoren deler det parametriske rum i de intervaller, der er nævnt før, normalt omtalt som knudevidder . Hver gang parameterværdien går ind i et nyt knobspænd, bliver et nyt kontrolpunkt aktivt, mens et gammelt kontrolpunkt kasseres. Det følger heraf, at værdierne i knudevektoren skal være i ikke -faldende rækkefølge, så (0, 0, 1, 2, 3, 3) er gyldig, mens (0, 0, 2, 1, 3, 3) ikke er det.

Sammenhængende knuder kan have samme værdi. Dette definerer derefter et knudevidde på nul længde, hvilket indebærer, at to kontrolpunkter aktiveres samtidigt (og naturligvis deaktiveres to kontrolpunkter). Dette har indflydelse på kontinuiteten af den resulterende kurve eller dens højere derivater; for eksempel tillader det oprettelse af hjørner i en ellers glat NURBS -kurve. Et antal sammenfaldende knuder omtales undertiden som en knude med en vis mangfoldighed . Knob med multiplicitet to eller tre er kendt som dobbelt eller tredobbelt knob. Mangfoldigheden af en knude er begrænset til kurvens grad; da en større mangfoldighed ville opdele kurven i uensartede dele, og det ville efterlade kontrolpunkter ubrugte. For førstegrads NURBS er hver knude parret med et kontrolpunkt.

Knudevektoren starter normalt med en knude, der har multiplicitet lig med rækkefølgen. Dette giver mening, da dette aktiverer de kontrolpunkter, der har indflydelse på det første knudevidde. Tilsvarende ender knudevektoren normalt med en knude af den mangfoldighed. Kurver med sådanne knudevektorer starter og slutter i et kontrolpunkt.

Knudernes værdier styrer kortlægningen mellem inputparameteren og den tilsvarende NURBS -værdi. For eksempel, hvis en NURBS beskriver en sti gennem rummet over tid, styrer knuderne den tid, funktionen fortsætter forbi kontrolpunkterne. Med henblik på at repræsentere former er det dog kun forholdene mellem forskellen mellem knudeværdierne; i så fald producerer knudevektorerne (0, 0, 1, 2, 3, 3) og (0, 0, 2, 4, 6, 6) den samme kurve. Knudeværdiernes positioner påvirker kortlægningen af parameterrum til kurverum. Gengivelse af en NURBS -kurve udføres normalt ved at træde med et fast skridt gennem parameterområdet. Ved at ændre knobspændlængderne kan der bruges flere prøvepunkter i områder, hvor krumningen er høj. En anden anvendelse er i situationer, hvor parameterværdien har en vis fysisk betydning, for eksempel hvis parameteren er tid, og kurven beskriver bevægelsen af en robotarm. Knudspændlængderne oversættes derefter til hastighed og acceleration, som er afgørende for at få det rigtigt for at forhindre skade på robotarmen eller dets miljø. Denne fleksibilitet i kortlægningen refererer til udtrykket ikke -ensartet i NURBS.

Kun nødvendige for interne beregninger er knuder normalt ikke nyttige for brugerne af modelleringssoftware. Derfor gør mange modelleringsprogrammer ikke knuderne redigerbare eller endda synlige. Det er normalt muligt at etablere rimelige knudevektorer ved at se på variationen i kontrolpunkterne. Nyere versioner af NURBS -software (f.eks. Autodesk Maya og Rhinoceros 3D ) giver mulighed for interaktiv redigering af knudepositioner, men dette er betydeligt mindre intuitivt end redigering af kontrolpunkter.

Konstruktion af basisfunktionerne

B-spline-basisfunktionerne, der bruges til konstruktion af NURBS-kurver, betegnes normalt som , hvori svarer til det ^tte kontrolpunkt og svarer til graden af basisfunktionen. Parameterafhængigheden udelades ofte, så vi kan skrive . Definitionen af disse basisfunktioner er rekursiv i . Grad-0-funktionerne er stykkevis konstante funktioner . De er en på det tilsvarende knudevidde og nul alle andre steder. Effektivt er en lineær interpolation af og . De to sidstnævnte funktioner er ikke-nul for knudevidder, overlappende for knudevidder. Funktionen beregnes som ${\ displaystyle N_ {i, n} (u)}$ ${\ displaystyle i}$ ${\ displaystyle i}$ ${\ displaystyle n}$ ${\ displaystyle N_ {i, n}}$ ${\ displaystyle n}$ ${\ displaystyle N_ {i, 0}}$ ${\ displaystyle N_ {i, n}}$ ${\ displaystyle N_ {i, n-1}}$ ${\ displaystyle N_ {i+1, n-1}}$ ${\ displaystyle n}$ ${\ displaystyle n-1}$ ${\ displaystyle N_ {i, n}}$

Fra top til bund: Lineære basisfunktioner (blå) og (grøn) (top), deres vægtfunktioner og (midten) og den resulterende kvadratiske basisfunktion (nederst). Knobene er 0, 1, 2 og 2,5

{\ displaystyle N_ {1,1}}

{\ displaystyle N_ {2,1}}

{\ displaystyle f}

{\ displaystyle g}

{\ displaystyle N_ {i, n} = f_ {i, n} N_ {i, n-1}+g_ {i+1, n} N_ {i+1, n-1}}

${\ displaystyle f_ {i}}$ stiger lineært fra nul til en i intervallet hvor er ikke-nul, mens det falder fra en til nul på intervallet hvor er ikke-nul. Som nævnt før er en trekantet funktion, uden nul over to knobspændinger, der stiger fra nul til en på den første og falder til nul på den anden knudevidde. Højere ordens basisfunktioner er ikke-nul over tilsvarende flere knudevidder og har tilsvarende højere grad. Hvis er parameteren, og er den ^th knude, kan vi skrive de funktioner og som ${\ displaystyle N_ {i, n-1}}$ ${\ displaystyle g_ {i+1}}$ ${\ displaystyle N_ {i+1, n-1}}$ ${\ displaystyle N_ {i, 1}}$ ${\ displaystyle u}$ ${\ displaystyle k_ {i}}$ ${\ displaystyle i}$ ${\ displaystyle f}$ ${\ displaystyle g}$

{\ displaystyle f_ {i, n} (u) = {{u-k_ {i}} \ over {k_ {i+n} -k_ {i}}}}

og

{\ displaystyle g_ {i, n} (u) = 1-f_ {i, n} (u) = {{k_ {i+n} -u} \ over {k_ {i+n} -k_ {i} }}}

Funktionerne og er positive, når de tilsvarende lavere ordens basisfunktioner ikke er nul. Ved induktion på n følger det, at basisfunktionerne er ikke-negative for alle værdier af og . Dette gør beregningen af basisfunktionerne numerisk stabil. ${\ displaystyle f}$ ${\ displaystyle g}$ ${\ displaystyle n}$ ${\ displaystyle u}$

Igen ved induktion kan det bevises, at summen af basisfunktionerne for en bestemt værdi af parameteren er enhed. Dette er kendt som opdeling af enhedens egenskab af basisfunktionerne.

Lineære basisfunktioner

Kvadratiske grundfunktioner

Figurerne viser de lineære og kvadratiske basisfunktioner for knuderne {..., 0, 1, 2, 3, 4, 4.1, 5.1, 6.1, 7.1, ...}

Et knobespænd er betydeligt kortere end de andre. På dette knudevidde er toppen i den kvadratiske basisfunktion mere tydelig og når næsten en. Omvendt falder de tilstødende basisfunktioner hurtigere til nul. I den geometriske fortolkning betyder det, at kurven nærmer sig det tilsvarende kontrolpunkt tæt. I tilfælde af en dobbelt knude bliver længden af knudevidden nul, og toppen når en præcis. Basisfunktionen er ikke længere differentierbar på det tidspunkt. Kurven vil have et skarpt hjørne, hvis nabokontrolpunkterne ikke er kollinære.

Generel form for en NURBS -kurve

Ved hjælp af definitionerne af basisfunktionerne fra det foregående afsnit har en NURBS -kurve følgende form: ${\ displaystyle N_ {i, n}}$

{\ displaystyle C (u) = \ sum _ {i = 1}^{k} {\ frac {N_ {i, n} (u) w_ {i}} {\ sum _ {j = 1}^{k } N_ {j, n} (u) w_ {j}}} \ mathbf {P} _ {i} = {\ frac {\ sum _ {i = 1}^{k} {N_ {i, n} ( u) w_ {i} \ mathbf {P} _ {i}}} {\ sum _ {i = 1}^{k} {N_ {i, n} (u) w_ {i}}}}}}

I dette er antallet af kontrolpunkter og er de tilsvarende vægte. Nævneren er en normaliserende faktor, der vurderer til en, hvis alle vægte er ét. Dette kan ses fra opdelingen af enhedens egenskab af basisfunktionerne. Det er sædvanligt at skrive dette som ${\ displaystyle k}$ ${\ displaystyle \ mathbf {P} _ {i}}$ ${\ displaystyle w_ {i}}$

{\ displaystyle C (u) = \ sum _ {i = 1}^{k} R_ {i, n} (u) \ mathbf {P} _ {i}}

hvori funktionerne

{\ displaystyle R_ {i, n} (u) = {N_ {i, n} (u) w_ {i} \ over \ sum _ {j = 1}^{k} N_ {j, n} (u) w_ {j}}}

er kendt som de rationelle basisfunktioner .

Generel form for en NURBS overflade

En NURBS overflade opnås som det tensor produkt af to NURBS kurver, således under anvendelse af to uafhængige parametre og (med indekser og henholdsvis): ${\ displaystyle u}$ ${\ displaystyle v}$ ${\ displaystyle i}$ ${\ displaystyle j}$

{\ displaystyle S (u, v) = \ sum _ {i = 1}^{k} \ sum _ {j = 1}^{l} R_ {i, j} (u, v) \ mathbf {P} _ {i, j}}

med

{\ displaystyle R_ {i, j} (u, v) = {\ frac {N_ {i, n} (u) N_ {j, m} (v) w_ {i, j}} {\ sum _ {p = 1}^{k} \ sum _ {q = 1}^{l} N_ {p, n} (u) N_ {q, m} (v) w_ {p, q}}}}

som rationelle grundfunktioner.

Manipulering af NURBS -objekter

Motoryacht -design ved hjælp af NURBS -overflader

Et antal transformationer kan anvendes på et NURBS -objekt. For eksempel, hvis en kurve er defineret ved hjælp af en bestemt grad og N kontrolpunkter, kan den samme kurve udtrykkes ved hjælp af den samme grad og N+1 kontrolpunkter. I processen ændrer et antal kontrolpunkter position, og en knude indsættes i knudevektoren. Disse manipulationer bruges i vid udstrækning under interaktivt design. Når man tilføjer et kontrolpunkt, skal kurvens form forblive den samme og danne udgangspunktet for yderligere justeringer. En række af disse operationer diskuteres nedenfor.

Knot indsættelse

Som udtrykket antyder, indsætter knude en knude i knudevektoren. Hvis kurvens grad er , erstattes kontrolpunkterne med nye. Kurvens form forbliver den samme. ${\ displaystyle n}$ ${\ displaystyle n-1}$ ${\ displaystyle n}$

En knude kan indsættes flere gange, op til den maksimale multiplicitet af knuden. Dette kaldes undertiden som knudeforfining og kan opnås ved en algoritme, der er mere effektiv end gentagen knudeindsættelse.

Fjernelse af knude

Knudfjernelse er omvendt af knudeindsættelse. Dens formål er at fjerne knuder og de tilhørende kontrolpunkter for at få en mere kompakt repræsentation. Dette er naturligvis ikke altid muligt, medens den nøjagtige form af kurven bevares. I praksis bruges en tolerance i nøjagtigheden til at afgøre, om en knude kan fjernes. Processen bruges til at rydde op efter en interaktiv session, hvor kontrolpunkter kan være tilføjet manuelt eller efter at have importeret en kurve fra en anden repræsentation, hvor en ligetil konverteringsproces fører til redundante kontrolpunkter.

Gradhøjde

En NURBS -kurve af en bestemt grad kan altid repræsenteres af en NURBS -kurve med højere grad. Dette bruges ofte, når man kombinerer separate NURBS -kurver, f.eks. Når man opretter en NURBS -overflade, der interpolerer mellem et sæt NURBS -kurver eller når man forener tilstødende kurver. I processen skal de forskellige kurver bringes i samme grad, normalt den maksimale grad af kurvesættet. Processen er kendt som grad elevation .

Krumning

Den vigtigste egenskab i differentialgeometri er krumningen . Den beskriver de lokale egenskaber (kanter, hjørner osv.) Og forholdet mellem det første og andet derivat og dermed den præcise kurveform. Efter at have bestemt derivaterne er det let at beregne eller tilnærme sig som arklængden fra det andet derivat . Den direkte beregning af krumningen med disse ligninger er den store fordel ved parameteriserede kurver i forhold til deres polygonale repræsentationer. ${\ displaystyle \ kappa}$ ${\ displaystyle \ kappa = {\ frac {| r '(t) \ gange r' '(t) |} {| r' (t) |^{3}}}}$ ${\ displaystyle \ kappa = | r '' (s_ {o}) |}$ ${\ displaystyle \ kappa}$

Eksempel: en cirkel

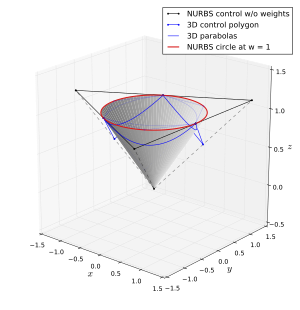
NURBS har evnen til nøjagtigt at beskrive cirkler. Her er den sorte trekant kontrolpolygonen i en NURBS -kurve (vist ved w = 1). Den blå stiplede linje viser den tilsvarende kontrolpolygon for en B-spline-kurve i homogene 3D- koordinater , dannet ved at gange NURBS med kontrolpunkterne med de tilsvarende vægte. De blå paraboler er den tilsvarende B-spline-kurve i 3D, der består af tre paraboler. Ved at vælge NURBS -kontrolpunkter og -vægte er parabolerne parallelle med den modsatte side af den grå kegle (med spidsen ved 3D -oprindelsen), så dividere med w for at projicere parabolerne på w = 1 -planet resulterer i cirkulære buer ( rød cirkel; se keglesnit ).

Ikke-rationelle splines eller Bézier-kurver kan tilnærme en cirkel, men de kan ikke repræsentere den nøjagtigt. Rationelle splines kan repræsentere enhver keglesnit, herunder cirklen, nøjagtigt. Denne repræsentation er ikke unik, men en mulighed vises nedenfor:

x	y	Vægt
1	0	1
1	1	${\ displaystyle \ scriptstyle {\ frac {\ sqrt {2}} {2}}}$
0	1	1
-1	1	${\ displaystyle \ scriptstyle {\ frac {\ sqrt {2}} {2}}}$
-1	0	1
-1	-1	${\ displaystyle \ scriptstyle {\ frac {\ sqrt {2}} {2}}}$
0	-1	1
1	-1	${\ displaystyle \ scriptstyle {\ frac {\ sqrt {2}} {2}}}$
1	0	1

Rækkefølgen er tre, da en cirkel er en kvadratisk kurve, og splinens rækkefølge er en mere end graden af dens stykkevise polynomiske segmenter. Knudevektoren er . Cirklen består af fire kvarte cirkler, bundet sammen med dobbelt knob. Selvom dobbeltknob i en tredje rækkefølge NURBS -kurve normalt ville resultere i tab af kontinuitet i det første derivat, er kontrolpunkterne placeret på en sådan måde, at det første derivat er kontinuerligt. Faktisk er kurven uendeligt differentieret overalt, som den må være, hvis den præcist repræsenterer en cirkel. ${\ displaystyle \ {0,0,0, \ pi /2, \ pi /2, \ pi, \ pi, 3 \ pi /2,3 \ pi /2,2 \ pi, 2 \ pi, 2 \ pi \} \,}$

Kurven repræsenterer en cirkel nøjagtigt, men den er ikke ligefrem parametriseret i cirkelens buelængde. Det betyder f.eks., At punktet at ikke ligger ved (undtagen start-, midter- og slutpunktet for hver kvartcirkel, da repræsentationen er symmetrisk). Dette ville være umuligt, da cirkelens x -koordinat ville give et nøjagtigt rationelt polynomisk udtryk for , hvilket er umuligt. Cirklen laver en fuld omdrejning, da dens parameter går fra 0 til , men dette er kun fordi knudevektoren vilkårligt blev valgt som multipler af . ${\ displaystyle t}$ ${\ displaystyle (\ sin (t), \ cos (t))}$ ${\ displaystyle \ cos (t)}$ ${\ displaystyle t}$ ${\ displaystyle 2 \ pi}$ ${\ displaystyle \ pi /2}$

Se også

Referencer

^ Schneider, Philip. "NURB -kurver: En guide til de uindviede" . MACTECH . Hentet 26. september 2014 .
^ Schoenberg, IJ (19. august 1964). "Spline -funktioner og problemet med eksamen" . Procedurer fra National Academy of Sciences i Amerikas Forenede Stater . National Academy of Sciences . 52 (4): 947–950. doi : 10.1073/pnas.52.4.947 . PMC 300377 . PMID 16591233 .
^ Foley, van Dam, Feiner & Hughes: Computer Graphics: Principles and Practice , afsnit 11.2, Addison-Wesley 1996 (2. udgave).
^ Bioinspireret selvorganiserende robotsystemer . s. 9 . Hentet 2014-01-06 .
^ "Rationelle B-splines" . www.cl.cam.ac.uk .
^ "NURBS: Definition" . www.cs.mtu.edu .
^ David F. Rogers: En introduktion til NURBS med historisk perspektiv, afsnit 7.1
^ Gershenfeld, Neil (1999). Matematisk modellerings natur . Cambridge University Press . s. 141. ISBN 0-521-57095-6.
^ ^a ^b ^c ^d Piegl, Les; Tiller, Wayne (1997). NURBS -bogen (2. red.). Berlin: Springer. ISBN 3-540-61545-8.
^ Piegl, L. (1989). "Ændring af formen på rationelle B-splines. Del 1: kurver". Computerstøttet design . 21 (8): 509–518. doi : 10.1016/0010-4485 (89) 90059-6 .

eksterne links

[mactech-1] Schneider, Philip. "NURB -kurver: En guide til de uindviede" . MACTECH . Hentet 26. september 2014 .

[2] Schoenberg, IJ (19. august 1964). "Spline -funktioner og problemet med eksamen" . Procedurer fra National Academy of Sciences i Amerikas Forenede Stater . National Academy of Sciences . 52 (4): 947–950. doi : 10.1073/pnas.52.4.947 . PMC 300377 . PMID 16591233 .

[3] Foley, van Dam, Feiner & Hughes: Computer Graphics: Principles and Practice , afsnit 11.2, Addison-Wesley 1996 (2. udgave).

[4] Bioinspireret selvorganiserende robotsystemer . s. 9 . Hentet 2014-01-06 .

[5] "Rationelle B-splines" . www.cl.cam.ac.uk .

[6] "NURBS: Definition" . www.cs.mtu.edu .

[7] David F. Rogers: En introduktion til NURBS med historisk perspektiv, afsnit 7.1

[8] Gershenfeld, Neil (1999). Matematisk modellerings natur . Cambridge University Press . s. 141. ISBN 0-521-57095-6.

[nurbs-book-9] Piegl, Les; Tiller, Wayne (1997). NURBS -bogen (2. red.). Berlin: Springer. ISBN 3-540-61545-8.

[10] Piegl, L. (1989). "Ændring af formen på rationelle B-splines. Del 1: kurver". Computerstøttet design . 21 (8): 509–518. doi : 10.1016/0010-4485 (89) 90059-6 .

Languages

In other projects