Sekvens - Sequence

I matematik er en sekvens en opregnet samling af objekter, hvor gentagelser er tilladt, og rækkefølge betyder noget. Ligesom et sæt indeholder det medlemmer (også kaldet elementer eller udtryk ). Antallet af elementer (muligvis uendeligt) kaldes længden af sekvensen. I modsætning til et sæt kan de samme elementer vises flere gange på forskellige positioner i en sekvens, og i modsætning til et sæt har rækkefølgen betydning. Formelt kan en sekvens defineres som en funktion fra naturlige tal (positionerne af elementer i sekvensen) til elementerne i hver position. Forestillingen om en sekvens kan generaliseres til en indekseret familie , defineret som en funktion fra et indekssæt, der muligvis ikke er tal til et andet sæt elementer.

For eksempel (M, A, R, Y) er en bogstavsekvens med bogstavet 'M' først og 'Y' sidst. Denne sekvens adskiller sig fra (A, R, M, Y). Sekvensen (1, 1, 2, 3, 5, 8), som indeholder tallet 1 på to forskellige positioner, er også en gyldig sekvens. Sekvenser kan være begrænsede , som i disse eksempler, eller uendelige , såsom sekvensen for alle endda positive heltal (2, 4, 6, ...).

Placeringen af ​​et element i en sekvens er dets rang eller indeks ; det er det naturlige tal, som elementet er billedet for. Det første element har indeks 0 eller 1, afhængigt af konteksten eller en specifik konvention. I matematisk analyse , er en sekvens, ofte betegnet med bogstaver i form af , og , hvor indekset n betegner den n th element af sekvensen; for eksempel betegnes det n. element i Fibonacci -sekvensen generelt som . ${\ displaystyle a_ {n}}$${\ displaystyle b_ {n}}$${\ displaystyle c_ {n}}$ ${\ displaystyle F}$${\ displaystyle F_ {n}}$

I computing og datalogi kaldes endelige sekvenser undertiden for strenge , ord eller lister , de forskellige navne svarer sædvanligvis til forskellige måder at repræsentere dem i computerens hukommelse ; uendelige sekvenser kaldes strømme . Den tomme sekvens () er inkluderet i de fleste begreber om sekvens, men kan udelukkes afhængigt af konteksten.

En uendelig rækkefølge af reelle tal (i blåt). Denne sekvens er hverken stigende, faldende, konvergent eller Cauchy . Det er dog afgrænset.

Eksempler og notation

En sekvens kan betragtes som en liste over elementer med en bestemt rækkefølge. Sekvenser er nyttige i en række matematiske discipliner til at studere funktioner , rum og andre matematiske strukturer ved hjælp af sekvensers konvergensegenskaber . Især sekvenser er grundlaget for serier , som er vigtige i differentialligninger og analyse . Sekvenser er også af interesse i sig selv og kan studeres som mønstre eller gåder, såsom i studiet af primtal .

Der er en række måder at betegne en sekvens, hvoraf nogle er mere nyttige til bestemte typer sekvenser. En måde at angive en sekvens på er at liste alle dens elementer. For eksempel danner de fire første ulige tal sekvensen (1, 3, 5, 7). Denne notation bruges også til uendelige sekvenser. For eksempel skrives den uendelige sekvens af positive ulige heltal som (1, 3, 5, 7, ...). Fordi notering af sekvenser med ellipse fører til tvetydighed, er notering mest nyttig for sædvanlige uendelige sekvenser, der let kan genkendes fra deres første få elementer. Andre måder at betegne en sekvens på diskuteres efter eksemplerne.

Eksempler

En flisebelægning med firkanter, hvis sider er successive Fibonacci -tal i længden.

De primtal er de naturlige tal større end 1, der ikke har nogen divisorer , men en og sig selv. At tage disse i deres naturlige rækkefølge giver sekvensen (2, 3, 5, 7, 11, 13, 17, ...). Primtalene er meget udbredt i matematik , især i talteori, hvor der findes mange resultater relateret til dem.

De Fibonacci tal omfatter det hele tal sekvens, hvis elementer er summen af de to foregående elementer. De to første elementer er enten 0 og 1 eller 1 og 1, så sekvensen er (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...).

Andre eksempler på sekvenser omfatter dem, der består af rationelle tal , reelle tal og komplekse tal . Sekvensen (.9, .99, .999, .9999, ...) nærmer sig for eksempel tallet 1. Faktisk kan hvert reelt tal skrives som grænsen for en sekvens af rationelle tal (f.eks. Via dets decimaludvidelse ). Som et andet eksempel er π grænsen for sekvensen (3, 3.1, 3.14, 3.141, 3.1415, ...), som er stigende. En beslægtet sekvens er sekvensen med decimalcifre på π , det vil sige (3, 1, 4, 1, 5, 9, ...). I modsætning til den foregående sekvens har denne sekvens ikke noget mønster, der let kan ses ved inspektion.

Den oeis omfatter en lang liste af eksempler på heltal sekvenser.

Indeksering

Andre notationer kan være nyttige til sekvenser, hvis mønster ikke let kan gættes eller til sekvenser, der ikke har et mønster, f.eks. Cifrene i π . En sådan notation er at nedskrive en generel formel til beregning af n. Udtryk som en funktion af n , omslutte det i parentes og inkludere et subscript, der angiver det sæt værdier, som n kan tage. For eksempel kan sekvensen af ​​lige tal i denne notation skrives som . Firkantssekvensen kunne skrives som . Variablen n kaldes et indeks , og det sæt værdier, det kan tage, kaldes indekssæt . ${\ displaystyle (2n) _ {n \ in \ mathbb {N}}}$${\ displaystyle (n^{2}) _ {n \ in \ mathbb {N}}}$

Det er ofte nyttigt at kombinere denne notation med teknikken til at behandle elementerne i en sekvens som individuelle variabler. Dette giver udtryk gerne , som angiver en sekvens, hvis n th element er givet ved den variable . For eksempel: ${\ displaystyle (a_ {n}) _ {n \ in \ mathbb {N}}}$${\ displaystyle a_ {n}}$

${\ displaystyle {\ begin {align} a_ {1} & = 1 {\ text {st element of}} (a_ {n}) _ {n \ in \ mathbb {N}} \\ a_ {2} & = 2 {\ text {nd element}} \\ a_ {3} & = 3 {\ text {rd element}} \\ & \; \; \ vdots \\ a_ {n-1} & = (n-1) {\ text {th element}} \\ a_ {n} & = n {\ text {th element}} \\ a_ {n+1} & = (n+1) {\ text {th element}} \\ & \; \; \ vdots \ end {align}}}$

Man kan overveje flere sekvenser på samme tid ved at bruge forskellige variabler; f.eks. kunne være en anden sekvens end . Man kan endda overveje en sekvens af sekvenser: betegner en sekvens, hvis m term er sekvensen . ${\ displaystyle (b_ {n}) _ {n \ in \ mathbb {N}}}$${\ displaystyle (a_ {n}) _ {n \ in \ mathbb {N}}}$${\ displaystyle ((a_ {m, n}) _ {n \ in \ mathbb {N}}) _ {m \ in \ mathbb {N}}}$${\ displaystyle (a_ {m, n}) _ {n \ i \ mathbb {N}}}$

Et alternativ til at skrive domænet for en sekvens i abonnementet er at angive det interval af værdier, som indekset kan tage ved at angive dets højeste og laveste juridiske værdier. For eksempel angiver notationen den ti-termede sekvens af firkanter . Grænserne og er tilladt, men de repræsenterer ikke gyldige værdier for indekset, henholdsvis kun over- eller minimum af sådanne værdier. For eksempel er sekvensen den samme som sekvensen og indeholder ikke et yderligere udtryk "i det uendelige". Sekvensen er en bi-uendelig sekvens og kan også skrives som . ${\ displaystyle (k^{2}) _ {k = 1}^{10}}$${\ displaystyle (1,4,9, \ ldots, 100)}$${\ displaystyle \ infty}$${\ displaystyle -\ infty}$${\ displaystyle (a_ {n}) _ {n = 1}^{\ infty}}$${\ displaystyle (a_ {n}) _ {n \ in \ mathbb {N}}}$${\ displaystyle (a_ {n}) _ {n =-\ infty}^{\ infty}}$${\ displaystyle (\ ldots, a _ {-1}, a_ {0}, a_ {1}, a_ {2}, \ ldots)}$

I tilfælde, hvor sættet med indekseringstal forstås, bliver abonnementerne og overskrifterne ofte udeladt. Det vil sige, at man simpelthen skriver for en vilkårlig sekvens. Ofte forstås indekset k at køre fra 1 til ∞. Imidlertid indekseres sekvenser ofte fra nul, som i ${\ displaystyle (a_ {k})}$

${\ displaystyle (a_ {k}) _ {k = 0}^{\ infty} = (a_ {0}, a_ {1}, a_ {2}, \ ldots).}$

I nogle tilfælde er elementerne i sekvensen naturligt relateret til en sekvens af heltal, hvis mønster let kan udledes. I disse tilfælde kan indekssættet være underforstået af en liste over de første få abstrakte elementer. F.eks. Kunne firkanten med ulige tal betegnes på en af ​​følgende måder.

• ${\ displaystyle (1,9,25, \ ldots)}$
• ${\ displaystyle (a_ {1}, a_ {3}, a_ {5}, \ ldots), \ qquad a_ {k} = k^{2}}$
• ${\ displaystyle (a_ {2k-1}) _ {k = 1}^{\ infty}, \ qquad a_ {k} = k^{2}}$
• ${\ displaystyle (a_ {k}) _ {k = 1}^{\ infty}, \ qquad a_ {k} = (2k-1)^{2}}$
• ${\ displaystyle \ left ((2k-1)^{2} \ right) _ {k = 1}^{\ infty}}$

Desuden kunne subscripts og superscripts have været udeladt i den tredje, fjerde og femte notation, hvis indekseringssættet forstås at være de naturlige tal . I den anden og tredje kugle er der en veldefineret sekvens , men den er ikke den samme som sekvensen angivet med udtrykket. ${\ displaystyle (a_ {k}) _ {k = 1}^{\ infty}}$

Definere en sekvens ved rekursion

Sekvenser, hvis elementer er relateret til de tidligere elementer på en ligetil måde, defineres ofte ved hjælp af rekursion . Dette er i modsætning til definitionen af ​​sekvenser af elementer som funktioner i deres positioner.

For at definere en sekvens ved rekursion har man brug for en regel, kaldet gentagelsesrelation for at konstruere hvert element i form af dem før det. Derudover skal der tilvejebringes nok indledende elementer til, at alle efterfølgende elementer i sekvensen kan beregnes ved successive applikationer af tilbagefaldsrelationen.

Den Fibonacci sekvens er et simpelt klassisk eksempel defineret af rekursionsligning

${\ displaystyle a_ {n} = a_ {n-1}+a_ {n-2},}$

med indledende vilkår og . Herfra viser en simpel beregning, at de første ti udtryk i denne sekvens er 0, 1, 1, 2, 3, 5, 8, 13, 21 og 34. ${\ displaystyle a_ {0} = 0}$${\ displaystyle a_ {1} = 1}$

Et kompliceret eksempel på en sekvens, der er defineret af en recurrence -relation, er Recamáns sekvens , defineret af recurrence -relationen

${\ displaystyle {\ begin {cases} a_ {n} = a_ {n-1} -n, \ quad {\ text {hvis resultatet er positivt og ikke allerede i de tidligere udtryk,}} \\ a_ {n} = a_ {n-1}+n, \ quad {\ text {ellers}}, \ end {cases}}}$

med indledende periode ${\ displaystyle a_ {0} = 0.}$

En lineær gentagelse med konstante koefficienter er en tilbagefaldsrelation af formen

${\ displaystyle a_ {n} = c_ {0}+c_ {1} a_ {n-1}+\ dots+c_ {k} a_ {nk},}$

hvor er konstanter . Der er en generel metode til at udtrykke det generelle udtryk for en sådan sekvens som en funktion af n ; se Lineær gentagelse . I tilfælde af Fibonacci -sekvensen har man og den resulterende funktion af n er givet ved Binets formel . ${\ displaystyle c_ {0}, \ dots, c_ {k}}$${\ displaystyle a_ {n}}$${\ displaystyle c_ {0} = 0, c_ {1} = c_ {2} = 1,}$

En holonomisk sekvens er en sekvens, der er defineret af en tilbagefaldsrelation af formen

${\ displaystyle a_ {n} = c_ {1} a_ {n-1} +\ dots +c_ {k} a_ {nk},}$

hvor er polynomer i n . For de fleste holonomiske sekvenser er der ingen eksplicit formel for udtrykkeligt at udtrykke som en funktion af n . Ikke desto mindre spiller holonomiske sekvenser en vigtig rolle inden for forskellige områder af matematik. For eksempel har mange specialfunktioner en Taylor -serie, hvis sekvens af koefficienter er holonomisk. Brugen af ​​gentagelsesrelationen muliggør en hurtig beregning af værdier for sådanne særlige funktioner. ${\ displaystyle c_ {1}, \ dots, c_ {k}}$${\ displaystyle a_ {n}}$

Ikke alle sekvenser kan specificeres ved en gentagelsesrelation. Et eksempel er sekvensen af primtal i deres naturlige rækkefølge (2, 3, 5, 7, 11, 13, 17, ...).

Formel definition og grundlæggende egenskaber

Der er mange forskellige forestillinger om sekvenser i matematik, hvoraf nogle ( f.eks . Nøjagtig sekvens ) ikke er omfattet af definitionerne og notationerne, der er introduceret nedenfor.

Definition

I denne artikel defineres en sekvens formelt som en funktion, hvis domæne er et interval af heltal . Denne definition dækker flere forskellige anvendelser af ordet "sekvens", herunder ensidige uendelige sekvenser, bi-uendelige sekvenser og endelige sekvenser (se nedenfor for definitioner af denne slags sekvenser). Mange forfattere bruger imidlertid en snævrere definition ved at kræve, at en sekvens domæne er et sæt af naturlige tal . Denne snævrere definition har den ulempe, at den udelukker endelige sekvenser og bi-uendelige sekvenser, som begge normalt kaldes sekvenser i standard matematisk praksis. En anden ulempe er, at hvis man fjerner de første vilkår i en sekvens, skal man genindeksere de resterende termer for at passe denne definition. I nogle sammenhænge, ​​for at forkorte eksponeringen, er kodens domæne i sekvensen fixet efter kontekst, for eksempel ved at kræve, at det er sættet R for reelle tal, sæt C for komplekse tal eller et topologisk rum .

Selvom sekvenser er en funktionstype, skelnes de sædvanligvis notationelt fra funktioner ved at input skrives som et subscript snarere end i parentes, det vil sige et _n frem for et ( n ) . Der er også terminologiske forskelle: værdien af ​​en sekvens ved det laveste input (ofte 1) kaldes "det første element" i sekvensen, værdien ved den næst mindste input (ofte 2) kaldes "det andet element", etc., mens en funktion, der indvindes sit input sædvanligvis er angivet ved et enkelt bogstav, f.eks også f , en sekvens, der indvindes dens indgang sædvanligvis skrevet af notation såsom , eller blot som her a er domænet, eller indekssæt, af sekvensen. ${\ displaystyle (a_ {n}) _ {n \ i A}}$${\ displaystyle (a_ {n}).}$

Sekvenser og deres grænser (se nedenfor) er vigtige begreber til at studere topologiske rum. En vigtig generalisering af sekvenser er begrebet net . Et net er en funktion fra et (muligvis utalligt ) rettet sæt til et topologisk rum. De notationelle konventioner for sekvenser gælder normalt også for net.

Endeligt og uendeligt

Den længde af en sekvens defineres som antallet af led i sekvensen.

En sekvens med en begrænset længde n kaldes også en n -dobbelt . Endelige sekvenser omfatter den tomme sekvens  (), der ikke har nogen elementer.

Normalt refererer udtrykket uendelig sekvens til en sekvens, der er uendelig i den ene retning, og endelig i den anden - sekvensen har et første element, men ikke noget sidste element. En sådan sekvens kaldes en enkelt uendelig sekvens eller en ensidig uendelig sekvens, når det er nødvendigt at fortælle om disambiguering. I modsætning hertil kaldes en sekvens, der er uendelig i begge retninger-dvs. der hverken har et første eller et sidste element-en bi-uendelig sekvens , to-vejs uendelig sekvens eller dobbelt uendelig sekvens . En funktion fra sættet Z for alle heltal til et sæt, f.eks. Sekvensen for alle lige heltal (..., −4, −2, 0, 2, 4, 6, 8, ...), er bi-uendelig. Denne sekvens kan betegnes . ${\ displaystyle (2n) _ {n =-\ infty}^{\ infty}}$

Stigende og faldende

En sekvens siges at være monotont stigende, hvis hvert udtryk er større end eller lig med det før det. For eksempel sekvensen er monotont voksende hvis og kun hvis en _{n +1} en _n for alle n ∈ N . Hvis hvert på hinanden følgende udtryk er strengt større end (>) det foregående udtryk, kaldes sekvensen strengt monotonisk stigende . En sekvens er monotont faldende , hvis hvert på hinanden følgende udtryk er mindre end eller lig med det foregående, og strengt monotont faldende , hvis hver er strengt mindre end det foregående. Hvis en sekvens enten stiger eller falder, kaldes den en monoton sekvens. Dette er et specielt tilfælde af den mere generelle opfattelse af en monoton funktion . ${\ displaystyle (a_ {n}) _ {n = 1}^{\ infty}}$ ${\ displaystyle \ geq}$

Begreberne ikke -stigende og ikke -stigende bruges ofte i stedet for stigende og faldende for at undgå enhver forveksling med henholdsvis strengt stigende og strengt faldende .

Afgrænset

Hvis sekvensen af ​​reelle tal ( a _n ) er sådan, at alle udtryk er mindre end et reelt tal M , siges sekvensen at være afgrænset ovenfra . Med andre ord betyder dette, at der eksisterer M sådan, at for alle n , en _n ≤ M . Enhver sådan M kaldes en øvre grænse . På samme måde, hvis for nogle reelle m , a _n ≥ m for alle n større end nogle N , så er sekvensen afgrænset nedenunder, og enhver sådan m kaldes en nedre grænse . Hvis en sekvens både er afgrænset ovenfra og afgrænset nedenunder, siges sekvensen at være afgrænset .

Efterfølgende

En undersekvens af en given sekvens er en sekvens dannet ud fra den givne sekvens ved at slette nogle af elementerne uden at forstyrre de relative positioners relative positioner. For eksempel er sekvensen af ​​positive lige heltal (2, 4, 6, ...) en undersekvens af de positive heltal (1, 2, 3, ...). Nogle elementers position ændres, når andre elementer slettes. De relative positioner bevares dog.

Formelt er en undersekvens af sekvensen enhver sekvens af formen , hvor der er en strengt stigende sekvens af positive heltal. ${\ displaystyle (a_ {n}) _ {n \ in \ mathbb {N}}}$${\ displaystyle (a_ {n_ {k}}) _ {k \ in \ mathbb {N}}}$${\ displaystyle (n_ {k}) _ {k \ in \ mathbb {N}}}$

Andre typer sekvenser

Nogle andre typer sekvenser, der er lette at definere, omfatter:

• En heltalssekvens er en sekvens, hvis termer er heltal.
• En polynom sekvens er en sekvens, hvis termer er polynomer.
• En positiv heltalssekvens kaldes undertiden multiplikativ , hvis a _nm = a _n a _m for alle par n , m sådan at n og m er coprime . I andre tilfælde kaldes sekvenser ofte multiplikative , hvis a _n = na ₁ for alle n . Desuden opfylder en multiplikativ Fibonacci -sekvens rekursionsrelationen a _n = a _{n −1} a _{n −2} .
• En binær sekvens er en sekvens, hvis termer har en af ​​to diskrete værdier, f.eks. Basis 2 -værdier (0,1,1,0, ...), en række møntkast (hoveder/haler) H, T, H, H , T, ..., svarene på et sæt sande eller falske spørgsmål (T, F, T, T, ...) osv.

Grænser og konvergens

Plottet af en konvergent sekvens ( a _n ) er vist med blåt. Fra grafen kan vi se, at sekvensen konvergerer til grænsen nul, når n stiger.

En vigtig egenskab ved en sekvens er konvergens . Hvis en sekvens konvergerer, konvergerer den til en bestemt værdi kendt som grænsen . Hvis en sekvens konvergerer til en vis grænse, er den konvergent . En sekvens, der ikke konvergerer, er divergerende .

Uformelt har en sekvens en grænse, hvis elementerne i sekvensen bliver tættere og tættere på en vis værdi (kaldet sekvensens grænse), og de bliver og forbliver vilkårligt tæt på , hvilket betyder, at givet et reelt tal større end nul, alt undtagen et begrænset antal af elementerne i sekvensen har en afstand fra mindre end . ${\ displaystyle L}$${\ displaystyle L}$${\ displaystyle d}$${\ displaystyle L}$${\ displaystyle d}$

For eksempel konvergerer den sekvens, der vises til højre, til værdien 0. På den anden side er sekvenserne (som begynder 1, 8, 27,…) og (som begynder −1, 1, −1, 1,…) begge divergerende. ${\ textstyle a_ {n} = {\ frac {n+1} {2n^{2}}}}$${\ textstyle b_ {n} = n^{3}}$${\ displaystyle c_ {n} = (-1)^{n}}$

Hvis en sekvens konvergerer, er værdien, den konvergerer til, unik. Denne værdi kaldes grænsen for sekvensen. Grænsen for en konvergent sekvens er normalt angivet . Hvis er en divergerende sekvens, så er udtrykket meningsløst. ${\ displaystyle (a_ {n})}$${\ textstyle \ lim _ {n \ to \ infty} a_ {n}}$${\ displaystyle (a_ {n})}$${\ textstyle \ lim _ {n \ to \ infty} a_ {n}}$

Formel definition af konvergens

En sekvens af reelle tal konvergerer til et reelt tal, hvis der for alle eksisterer et naturligt tal, så det for alle vi har ${\ displaystyle (a_ {n})}$ ${\ displaystyle L}$${\ displaystyle \ varepsilon> 0}$${\ displaystyle N}$${\ displaystyle n \ geq N}$

${\ displaystyle | a_ {n} -L | <\ varepsilon.}$

Hvis er en sekvens af komplekse tal snarere end en sekvens af reelle tal, kan denne sidste formel stadig bruges til at definere konvergens med den bestemmelse, at betegner den komplekse modulus, dvs. . Hvis er en sekvens af punkter i et metrisk rum , kan formlen bruges til at definere konvergens, hvis udtrykket erstattes af udtrykket , som angiver afstanden mellem og . ${\ displaystyle (a_ {n})}$${\ displaystyle | \ cdot |}$${\ displaystyle | z | = {\ sqrt {z^{*} z}}}$${\ displaystyle (a_ {n})}$${\ displaystyle | a_ {n} -L |}$${\ displaystyle \ operatorname {dist} (a_ {n}, L)}$${\ displaystyle a_ {n}}$${\ displaystyle L}$

Ansøgninger og vigtige resultater

Hvis og er konvergente sekvenser, eksisterer følgende grænser og kan beregnes som følger: ${\ displaystyle (a_ {n})}$${\ displaystyle (b_ {n})}$

• ${\ displaystyle \ lim _ {n \ to \ infty} (a_ {n} \ pm b_ {n}) = \ lim _ {n \ to \ infty} a_ {n} \ pm \ lim _ {n \ to \ infty} b_ {n}}$
• ${\ displaystyle \ lim _ {n \ to \ infty} ca_ {n} = c \ lim _ {n \ to \ infty} a_ {n}}$ for alle reelle tal ${\ displaystyle c}$
• ${\ displaystyle \ lim _ {n \ til \ infty} (a_ {n} b_ {n}) = \ venstre (\ lim _ {n \ til \ infty} a_ {n} \ højre) \ venstre (\ lim _ {n \ to \ infty} b_ {n} \ right)}$
• ${\ displaystyle \ lim _ {n \ to \ infty} {\ frac {a_ {n}} {b_ {n}}} = {\ frac {\ lim \ limit _ {n \ to \ infty} a_ {n} } {\ lim \ limit _ {n \ to \ infty} b_ {n}}}}$, forudsat at ${\ displaystyle \ lim _ {n \ to \ infty} b_ {n} \ neq 0}$
• ${\ displaystyle \ lim _ {n \ to \ infty} a_ {n}^{p} = \ left (\ lim _ {n \ to \ infty} a_ {n} \ right)^{p}}$for alle og${\ displaystyle p> 0}$${\ displaystyle a_ {n}> 0}$

I øvrigt:

• Hvis for alle større end nogle , så .${\ displaystyle a_ {n} \ leq b_ {n}}$${\ displaystyle n}$${\ displaystyle N}$${\ displaystyle \ lim _ {n \ to \ infty} a_ {n} \ leq \ lim _ {n \ to \ infty} b_ {n}}$
• ( Klem sætning )
  Hvis er en sekvens, der for alle og , så er konvergent, og .${\ displaystyle (c_ {n})}$${\ displaystyle a_ {n} \ leq c_ {n} \ leq b_ {n}}$${\ displaystyle n> N}$ ${\ displaystyle \ lim _ {n \ to \ infty} a_ {n} = \ lim _ {n \ to \ infty} b_ {n} = L}$
  ${\ displaystyle (c_ {n})}$${\ displaystyle \ lim _ {n \ to \ infty} c_ {n} = L}$
• Hvis en sekvens er afgrænset og monoton, er den konvergent.
• En sekvens er konvergent, hvis og kun hvis alle dens undersekvenser er konvergente.

Cauchy sekvenser

Plottet af en Cauchy -sekvens ( X _n ), vist med blåt, som X _n versus n . I grafen ser det ud til, at sekvensen konvergerer til en grænse, efterhånden som afstanden mellem på hinanden følgende termer i sekvensen bliver mindre, når n stiger. I de reelle tal konvergerer hver Cauchy -sekvens til en vis grænse.

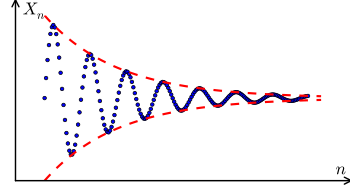
En Cauchy -sekvens er en sekvens, hvis vilkår bliver vilkårligt tæt sammen, når n bliver meget stor. Forestillingen om en Cauchy -sekvens er vigtig i studiet af sekvenser i metriske rum og især i reel analyse . Et særligt vigtigt resultat i reel analyse er Cauchy -karakterisering af konvergens for sekvenser :

En sekvens af reelle tal er konvergent (i realerne), hvis og kun hvis det er Cauchy.

Derimod er der Cauchy -sekvenser af rationelle tal , der ikke er konvergente i rationalerne, fx sekvensen defineret af x ₁ = 1 og x _{n +1} =x _n +2/x _n/2 er Cauchy, men har ingen rationel grænse, jf. her . Mere generelt er enhver sekvens af rationelle tal, der konvergerer til et irrationelt tal , Cauchy, men ikke konvergent, når den tolkes som en sekvens i sættet med rationelle tal.

Metriske rum, der tilfredsstiller Cauchy -karakteriseringen af ​​konvergens for sekvenser, kaldes komplette metriske rum og er særligt gode til analyse.

Uendelige grænser

I beregning er det almindeligt at definere notation for sekvenser, der ikke konvergerer i den forstand, der er diskuteret ovenfor, men som i stedet bliver og forbliver vilkårligt store eller bliver og forbliver vilkårligt negative. Hvis bliver vilkårligt stort som , skriver vi ${\ displaystyle a_ {n}}$${\ displaystyle n \ to \ infty}$

${\ displaystyle \ lim _ {n \ to \ infty} a_ {n} = \ infty.}$

I dette tilfælde siger vi, at sekvensen divergerer , eller at den konvergerer til uendelig . Et eksempel på en sådan sekvens er a _n = n .

Hvis bliver vilkårligt negativ (dvs. negativ og stor i omfang) som , skriver vi ${\ displaystyle a_ {n}}$${\ displaystyle n \ to \ infty}$

${\ displaystyle \ lim _ {n \ to \ infty} a_ {n} =-\ infty}$

og sige, at sekvensen divergerer eller konvergerer til negativ uendelighed .

Serie

En serie er uformelt set summen af ​​vilkårene i en sekvens. Det vil sige, det er et udtryk for formen, eller hvor er en sekvens af reelle eller komplekse tal. De partielle summer i en serie er udtrykkene følger erstatte uendelighedssymbolet med et endeligt antal, dvs. N th partielle sum af serien er antallet ${\ textstyle \ sum _ {n = 1}^{\ infty} a_ {n}}$${\ displaystyle a_ {1}+a_ {2}+\ cdots}$${\ displaystyle (a_ {n})}$${\ textstyle \ sum _ {n = 1}^{\ infty} a_ {n}}$

${\ displaystyle S_ {N} = \ sum _ {n = 1}^{N} a_ {n} = a_ {1}+a_ {2}+\ cdots+a_ {N}.}$

Delsummerne selv danner en sekvens , som kaldes sekvensen af ​​delsummer i serien . Hvis sekvensen af ​​delsummer summeres, så siger vi, at serien er konvergent , og grænsen kaldes seriens værdi . Den samme notation bruges til at betegne en serie og dens værdi, dvs. vi skriver . ${\ displaystyle (S_ {N}) _ {N \ in \ mathbb {N}}}$${\ textstyle \ sum _ {n = 1}^{\ infty} a_ {n}}$${\ textstyle \ sum _ {n = 1}^{\ infty} a_ {n}}$${\ textstyle \ lim _ {N \ to \ infty} S_ {N}}$${\ textstyle \ sum _ {n = 1}^{\ infty} a_ {n} = \ lim _ {N \ to \ infty} S_ {N}}$

Anvendelse inden for andre matematikområder

Topologi

Sekvenser spiller en vigtig rolle i topologi, især i studiet af metriske rum . For eksempel:

• Et metrisk rum er kompakt, nøjagtigt når det er sekventielt kompakt .
• En funktion fra et metrisk rum til et andet metrisk rum er kontinuerlig, præcis når det tager konvergente sekvenser til konvergente sekvenser.
• Et metrisk rum er et forbundet rum, hvis og kun hvis et af de to sæt, når rummet er opdelt i to sæt, indeholder en sekvens, der konvergerer til et punkt i det andet sæt.
• Et topologisk rum kan adskilles nøjagtigt, når der er en tæt sekvens af punkter.

Sekvenser kan generaliseres til net eller filtre . Disse generaliseringer gør det muligt at udvide nogle af ovenstående sætninger til mellemrum uden metrik.

Produkttopologi

Det topologiske produkt af en sekvens af topologiske rum er det kartesiske produkt af disse rum, udstyret med en naturlig topologi kaldet produkttopologien .

Mere formelt, givet en række rum , produktrummet ${\ displaystyle (X_ {i}) _ {i \ in \ mathbb {N}}}$

${\ displaystyle X: = \ prod _ {i \ in \ mathbb {N}} X_ {i},}$

er defineret som sættet af alle sekvenser, således at for hver i , er et element af . De kanoniske fremskrivninger er kortene p _i  : X → X _i defineret af ligningen . Derefter defineres produkttopologien på X til at være den groveste topologi (dvs. topologien med færrest åbne sæt), som alle fremskrivningerne p _i er kontinuerlige for . Produkttopologien kaldes undertiden Tychonoff -topologien . ${\ displaystyle (x_ {i}) _ {i \ in \ mathbb {N}}}$${\ displaystyle x_ {i}}$${\ displaystyle X_ {i}}$${\ displaystyle p_ {i} ((x_ {j}) _ {j \ in \ mathbb {N}}) = x_ {i}}$

Analyse

I analyse , når man taler om sekvenser, vil man generelt overveje sekvenser af formen

${\ displaystyle (x_ {1}, x_ {2}, x_ {3}, \ dots) {\ text {eller}} (x_ {0}, x_ {1}, x_ {2}, \ dots)}$

det vil sige uendelige sekvenser af elementer indekseret af naturlige tal .

Det kan være praktisk at få sekvensen til at starte med et indeks, der er forskelligt fra 1 eller 0. Sekvensen, der er defineret af x _n = 1/ log ( n ), vil f.eks. Kun blive defineret for n ≥ 2. Når man taler om sådanne uendelige sekvenser, det er normalt tilstrækkeligt (og ændrer sig ikke meget for de fleste overvejelser) for at antage, at medlemmerne af sekvensen er defineret i det mindste for alle indeks stort nok , dvs. større end en given N .

Den mest elementære type sekvenser er numeriske, det vil sige sekvenser af reelle eller komplekse tal. Denne type kan generaliseres til sekvenser af elementer i noget vektorrum . I analyse er de betragtede vektorrum ofte funktionsrum . Endnu mere generelt kan man studere sekvenser med elementer i et eller andet topologisk rum .

Sekvensrum

Et sekvensrum er et vektorrum, hvis elementer er uendelige sekvenser af reelle eller komplekse tal. Tilsvarende er det et funktionsrum, hvis elementer er funktioner fra de naturlige tal til feltet K , hvor K enten er feltet med reelle tal eller feltet med komplekse tal. Sættet af alle sådanne funktioner er naturligt identificeret med sættet af alle mulige uendelige sekvenser med elementer i K , og kan omdannes til et vektorrum under operationerne med punktvis tilføjelse af funktioner og punktvis skalær multiplikation. Alle sekvensrum er lineære underrum af dette rum. Sekvensrum er typisk udstyret med en norm eller i det mindste strukturen i et topologisk vektorrum .

De vigtigste sekvenser mellemrum i analysen er l ^p rum, som består af p -Power summable sekvenser, med p -normen. Disse er specielle tilfælde af L ^p -mellemrum til tællemålet på sættet med naturlige tal. Andre vigtige klasser af sekvenser som konvergente sekvenser eller null -sekvenser danner sekvensrum, henholdsvis betegnet c og c ₀ , med sup -normen. Ethvert sekvensrum kan også udstyres med topologien med punktvis konvergens , under hvilken det bliver til en særlig slags Fréchet-rum kaldet et FK-rum .

Lineær algebra

Sekvenser over et felt kan også ses som vektorer i et vektorrum . Konkret er sættet med F -værdiansatte sekvenser (hvor F er et felt) et funktionsrum (faktisk et produktrum ) med F -værdiansatte funktioner over sættet med naturlige tal.

Abstrakt algebra

Abstrakt algebra anvender flere typer sekvenser, herunder sekvenser af matematiske objekter som grupper eller ringe.

Gratis monoid

Hvis A er et sæt, er den frie monoid over A (betegnet A ^* , også kaldet Kleene stjerne i A ) en monoid, der indeholder alle de endelige sekvenser (eller strenge) af nul eller flere elementer af A , med den binære drift af sammenkædning. Den gratis halvgruppe A ⁺ er en undergruppe af A ^{*, der} indeholder alle elementer undtagen den tomme sekvens.

Præcise sekvenser

I forbindelse med gruppeteori , en sekvens

${\ displaystyle G_ {0} \; {\ xrightarrow {f_ {1}}} \; G_ {1} \; {\ xrightarrow {f_ {2}}} \; G_ {2} \; {\ xrightarrow {f_ {3}}} \; \ cdots \; {\ xrightarrow {f_ {n}}} \; G_ {n}}$

af grupper og gruppehomomorfier kaldes nøjagtig , hvis billedet (eller området ) af hver homomorfisme er lig med kernen i den næste:

${\ displaystyle \ mathrm {im} (f_ {k}) = \ mathrm {ker} (f_ {k+1})}}$

Sekvensen af ​​grupper og homomorfier kan enten være begrænset eller uendelig.

En lignende definition kan laves for visse andre algebraiske strukturer . For eksempel kan man have en nøjagtig sekvens af vektorrum og lineære kort eller moduler og modulhomomorfier .

Spektrale sekvenser

I homologisk algebra og algebraisk topologi er en spektral sekvens et middel til at beregne homologigrupper ved at tage successive tilnærmelser. Spektrale sekvenser er en generalisering af nøjagtige sekvenser , og siden deres introduktion af Jean Leray  ( 1946 ) er de blevet et vigtigt forskningsværktøj, især inden for homotopiteori .

Sætteori

En ordinalindekseret sekvens er en generalisering af en sekvens. Hvis α er en grænse ordenstal og X er et sæt, en α-indekseret sekvens af elementer i X er en funktion fra α til X . I denne terminologi er en ω-indekseret sekvens en almindelig sekvens.

Computing

I datalogi kaldes endelige sekvenser lister . Potentielt uendelige sekvenser kaldes strømme . Endelige sekvenser af tegn eller cifre kaldes strenge .

Vandløb

Uendelige sekvenser af cifre (eller tegn ) hentet fra et begrænset alfabet er af særlig interesse for teoretisk datalogi . De omtales ofte blot som sekvenser eller strømme , i modsætning til begrænsede strenge . Uendelige binære sekvenser er f.eks. Uendelige sekvenser af bits (tegn trukket fra alfabetet {0, 1}). Sættet C = {0, 1} ^∞ for alle uendelige binære sekvenser kaldes undertiden Cantor -rummet .

En uendelig binær sekvens kan repræsentere et formelt sprog (et sæt strenge) ved at indstille den n.  Bit af sekvensen til 1, hvis og kun hvis den n  th streng (i shortlex rækkefølge ) er i sproget. Denne fremstilling er nyttig i diagonaliseringsmetoden til beviser.

Se også

• Optælling
• Online encyklopædi af heltalssekvenser
• Tilbagevendende forhold
• Sekvensplads

Operationer

• Cauchy produkt

Eksempler

• Diskret tidssignal
• Farey sekvens
• Fibonacci -sekvens
• Se og sig sekvens
• Thue – Morse sekvens
• Liste over heltalsekvenser

Typer

• ± 1-sekvens
• Aritmetisk progression
• Automatisk sekvens
• Cauchy sekvens
• Konstant-rekursiv sekvens
• Geometrisk progression
• Harmonisk progression
• Holonomisk sekvens
• Regelmæssig rækkefølge
• Pseudotilfældig binær sekvens
• Tilfældig sekvens

Relaterede koncepter

• Liste (computing)
• Net (topologi) (en generalisering af sekvenser)
• Ordinalindekseret sekvens
• Rekursion (datalogi)
• Sæt (matematik)
• Tuple
• Permutation

Noter

Referencer

eksterne links

• "Sekvens" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• The Online Encyclopedia of Integer Sequences
• Journal of Integer Sequences (gratis)