Pontryagin dualitet - Pontryagin duality

I matematik er Pontryagin -dualitet en dualitet mellem lokalt kompakte abelske grupper, der tillader generalisering af Fourier -transformation til alle sådanne grupper, som omfatter cirkelgruppen (den multiplikative gruppe af komplekse tal med modul 1), de endelige abelske grupper (med den diskrete topologi ) og additivgruppen af heltalene (også med den diskrete topologi), de reelle tal og hvert endeligt dimensionelt vektorrum over realerne eller et p -adisk felt .

Den Pontryagin dobbelte af en lokalt kompakt abelsk gruppe, er gruppen dannet af de kontinuerlige gruppehomomorfi fra gruppen til cirklen gruppen. Den Pontryagin dualitetssætning indfører Pontryagin dobbelthed med, at enhver lokalt kompakt abelsk gruppe er naturligt isomorf med sin bidual (det dobbelte af sin dobbelte). Den Fourier inversion teorem er et specielt tilfælde af denne sætning.

Emnet er opkaldt efter Lev Pontryagin, der lagde grundlaget for teorien om lokalt kompakte abelske grupper og deres dobbelthed under sine tidlige matematiske værker i 1934. Pontryagins behandling var afhængig af, at gruppen var anden-tællelig og enten kompakt eller diskret. Dette blev forbedret til at dække de generelt lokalt kompakte abelske grupper af Egbert van Kampen i 1935 og André Weil i 1940.

Introduktion

Pontryagin -dualitet placerer i en samlet kontekst en række observationer om funktioner på den virkelige linje eller på begrænsede abelske grupper:

• Passende regelmæssige kompleksværdierede periodiske funktioner på den virkelige linje har Fourier-serier, og disse funktioner kan gendannes fra deres Fourier-serier;
• Passende regelmæssige kompleksværdierede funktioner på den virkelige linje har Fourier-transformationer, der også er funktioner på den reelle linje, og ligesom for periodiske funktioner kan disse funktioner gendannes fra deres Fourier-transformationer; og
• Kompleksværdierede funktioner på en endelig abelsk gruppe har diskrete Fourier-transformer , som er funktioner på den dobbelte gruppe , som er en (ikke-kanonisk) isomorf gruppe. Desuden kan enhver funktion på en endelig abelsk gruppe gendannes fra dens diskrete Fourier -transformation.

Teorien, introduceret af Lev Pontryagin og kombineret med Haar -målingen introduceret af John von Neumann , André Weil og andre, afhænger af teorien om dobbeltgruppen i en lokalt kompakt abelsk gruppe.

Det er analogt med et vektorrums dobbelte vektorrum : et endeligt-dimensionelt vektorrum V og dets dobbelte vektorrum V* er ikke naturligt isomorft, men endomorfisme- algebra (matrixalgebra) for et er isomorft i modsætning til endomorfismen den anden algebra: via transponeringen. Tilsvarende skal en gruppe og dens dobbelte gruppe , er ikke generelt isomorf, men deres endomorfien ringe er modsat hinanden: . Mere kategorisk er dette ikke bare en isomorfisme af endomorfisme -algebraer, men en kontravariant ækvivalens af kategorier - se kategoriske overvejelser . ${\ displaystyle {\ text {End}} (V) \ cong {{\ text {End}} (V^{*})}^{\ text {op}},}$${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle {\ text {End}} (G) \ cong {\ text {End}} ({\ widehat {G}})^{\ text {op}}}$

Definition

En topologisk gruppe er en lokalt kompakt gruppe, hvis det underliggende topologiske rum er lokalt kompakt og Hausdorff ; en topologisk gruppe er abelsk, hvis den underliggende gruppe er abelsk . Eksempler på lokalt kompakte abelske grupper inkluderer endelige abeliske grupper, heltalene (både for den diskrete topologi , som også induceres af den sædvanlige metriske), de reelle tal, cirkelgruppen T (begge med deres sædvanlige metriske topologi) og også p -adiske tal (med deres sædvanlige p -adiske topologi).

For en lokalt kompakt abelsk gruppe er Pontryagin dual gruppen af kontinuerlige gruppehomomorfier fra til cirkelgruppen . Det er, ${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle G}$${\ displaystyle T}$

${\ displaystyle {\ widehat {G}}: = \ operatorname {Hom} (G, T).}$

Pontryagin dual er normalt udstyret med topologien givet ved ensartet konvergens på kompakte sæt (det vil sige topologien forårsaget af den kompakte åbne topologi på rummet for alle kontinuerlige funktioner fra til ). ${\ displaystyle {\ widehat {G}}}$${\ displaystyle G}$${\ displaystyle T}$

For eksempel,

${\ displaystyle {\ widehat {\ mathbb {Z}}} = T, \ {\ widehat {\ mathbb {R}}} = \ mathbb {R}, \ {\ widehat {T}} = \ mathbb {Z} .}$

Pontryagins dualitetsteorem

Sætning : Der er en kanonisk isomorfisme   mellem enhver lokalt kompakt abelsk gruppe og dens dobbelte dual.${\ displaystyle G \ cong {\ widehat {\ widehat {G}}}}$${\ displaystyle G}$

Kanonisk betyder, at der er et naturligt defineret kort  ; endnu vigtigere, kortet skal have funktionalitet i . Den kanoniske isomorfisme defineres på følgende måde: ${\ displaystyle \ operatorname {ev} _ {G} \ colon G \ to {\ widehat {\ widehat {G}}}}}$${\ displaystyle G}$${\ displaystyle \ operatorname {ev} _ {G}}$${\ displaystyle x \ i G}$

${\ displaystyle \ operatorname {ev} _ {G} (x) (\ chi) = \ chi (x) \ in \ mathbb {T}. \ {\ text {Det vil sige}} \ \ operatorname {ev} _ {G} (x): (\ chi \ mapsto \ chi (x)).}$

Med andre ord er hvert gruppeelement identificeret til evalueringstegnet på det dobbelte. Dette er stærkt analog med den kanoniske isomorfi mellem en finite-dimensionalt vektorrum og dets dobbelte dobbelt , og det er værd at nævne, at enhver vektorrum er en Abelian gruppe . Hvis er en endelig abelsk gruppe, men denne isomorfisme er ikke kanonisk. At præcisere denne erklæring (generelt) kræver at tænke på dualisering ikke kun på grupper, men også på kort mellem grupperne, for at behandle dualisering som en funktor og bevise, at identitetsfunktoren og dualiseringsfunktoren ikke naturligt er ækvivalente. Dualitetsteoremet indebærer også, at dualiseringsfunktoren for enhver gruppe (ikke nødvendigvis begrænset) er en nøjagtig funktor. ${\ displaystyle x}$${\ displaystyle V \ cong V^{**}}$${\ displaystyle V}$${\ displaystyle G}$${\ displaystyle G \ cong {\ widehat {G}}}$

Pontryagin -dualitet og Fourier -transformationen

Haar måling

En af de mest bemærkelsesværdige fakta om en lokalt kompakt gruppe er, at den bærer et i det væsentlige unikt naturligt mål , Haar -målingen , som gør det muligt konsekvent at måle "størrelsen" af tilstrækkeligt regelmæssige undersæt af . "Tilstrækkeligt regelmæssig delmængde" betyder her et Borel -sæt ; det vil sige et element i σ-algebra genereret af de kompakte sæt . Mere præcist er en højre Haar -måling på en lokalt kompakt gruppe et tal, der er additivt μ μ defineret på Borelsættene, og som er ret invariant i den forstand, at μ ( Ax ) = μ ( A ) for et element af og en Borel -delmængde af og opfylder også visse regelmæssighedsbetingelser (beskrevet detaljeret i artiklen om Haar -måling ). Bortset fra positive skaleringsfaktorer er et Haar -mål unikt. ${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle x}$${\ displaystyle G}$${\ displaystyle A}$${\ displaystyle G}$${\ displaystyle G}$

Haar -målingen giver os mulighed for at definere begrebet integral for ( komplekse -værdsatte) Borel -funktioner defineret i gruppen. Især kan man overveje forskellige L ^p -rum, der er forbundet med Haar -måling μ. Specifikt, ${\ displaystyle G}$

${\ displaystyle {\ mathcal {L}} _ {\ mu}^{p} (G) = \ venstre \ {(f: G \ til \ mathbb {C}) \ {\ Big |} \ \ int _ { G} | f (x) |^{p} \ d \ mu (x) <\ infty \ right \}.}$

Bemærk, at da to Haar -mål på er lig med en skaleringsfaktor, er dette –rum uafhængigt af valget af Haar -mål og kan derfor måske skrives som . Imidlertid er –normen på dette rum afhængig af valget af Haar -mål, så hvis man vil tale om isometrier, er det vigtigt at holde styr på den Haar -måling, der bruges. ${\ displaystyle G}$${\ displaystyle L^{p}}$${\ displaystyle L^{p} (G)}$${\ displaystyle L^{p}}$

Fourier transform og Fourier inversions formel for L ¹ -funktioner

Dobbeltgruppen i en lokalt kompakt abelsk gruppe bruges som det underliggende rum for en abstrakt version af Fourier -transformationen . Hvis , derefter Fourier transformationen er funktionen på defineret ved ${\ displaystyle f \ i L^{1} (G)}$${\ displaystyle {\ widehat {f}}}$${\ displaystyle {\ widehat {G}}}$

${\ displaystyle {\ widehat {f}} (\ chi) = \ int _ {G} f (x) {\ overline {\ chi (x)}} \ d \ mu (x),}$

hvor integralet er i forhold til Haar måle på . Dette er også betegnet . Bemærk Fourier -transformationen afhænger af valget af Haar -mål. Det er ikke for svært at vise, at Fourier -transformationen af ​​en funktion på er en afgrænset kontinuerlig funktion, som forsvinder i det uendelige . ${\ displaystyle \ mu}$${\ displaystyle G}$${\ displaystyle ({\ mathcal {F}} f) (\ chi)}$${\ displaystyle L^{1}}$${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$

Fourier Inversionsformel for -Funktioner. ${\ displaystyle L^{1}}$For hvert Haar foranstaltning på der er en unik Haar foranstaltning på sådan, at hver gang , og vi har ${\ displaystyle \ mu}$${\ displaystyle G}$${\ displaystyle \ nu}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle f \ i L^{1} (G)}$${\ displaystyle {\ widehat {f}} \ i L^{1} \ venstre ({\ widehat {G}} \ højre)}$

${\ displaystyle f (x) = \ int _ {\ widehat {G}} {\ widehat {f}} (\ chi) \ chi (x) \ d \ nu (\ chi) \ qquad \ mu {\ text { -næsten overalt}}}$

Hvis den er kontinuerlig, gælder denne identitet for alle .${\ displaystyle f}$${\ displaystyle x}$

Den inverse Fouriertransformation af en integrerbar funktion på er givet af ${\ displaystyle {\ widehat {G}}}$

${\ displaystyle {\ check {g}} (x) = \ int _ {\ widehat {G}} g (\ chi) \ chi (x) \ d \ nu (\ chi),}$

hvor integralet er i forhold til Haar -målingen på dobbeltgruppen . Foranstaltningen på , der vises i Fourier inversion formel kaldes dobbelte foranstaltning til og kan betegnes . ${\ displaystyle \ nu}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle \ nu}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle \ mu}$${\ displaystyle {\ widehat {\ mu}}}$

De forskellige Fourier -transformationer kan klassificeres i form af deres domæne og transformationsdomæne (gruppen og dobbeltgruppen) som følger (bemærk, det er cirkelgruppe ): ${\ displaystyle \ mathbb {T}}$

Transform	Oprindeligt domæne, ${\ displaystyle G}$	Transformér domæne, ${\ displaystyle {\ hat {G}}}$	Måle, ${\ displaystyle \ mu}$
Fourier transform	${\ displaystyle \ mathbb {R}}$	${\ displaystyle \ mathbb {R}}$	${\ displaystyle {\ text {Constant}} \ times {\ text {Lebesgue -måling}}}$
Fourier -serien	${\ displaystyle \ mathbb {T}}$	${\ displaystyle \ mathbb {Z}}$	${\ displaystyle {\ text {Constant}} \ times {\ text {Lebesgue -måling}}}$
Diskret tid Fourier-transformation (DTFT)	${\ displaystyle \ mathbb {Z}}$	${\ displaystyle \ mathbb {T}}$	${\ displaystyle {\ text {Constant}} \ times {\ text {Counting measure}}}$
Diskret Fouriertransformation (DFT)	${\ displaystyle \ mathbb {Z} _ {n}}$	${\ displaystyle \ mathbb {Z} _ {n}}$	${\ displaystyle {\ text {Constant}} \ times {\ text {Counting measure}}}$

Som et eksempel antage , så vi kan tænke på som ved parring Hvis er Lebesgue mål om euklidisk rum, får vi det sædvanlige Fouriertransformation på og den dobbelte foranstaltning er nødvendig for Fourier inversion formel er . Hvis vi ønsker at få en Fourier inversionsformel med det samme mål på begge sider (det vil sige, da vi kan tænke på det som sit eget dobbeltrum, kan vi bede om at blive lig med ), så skal vi bruge ${\ displaystyle G = \ mathbb {R} ^{n}}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e^{i \ mathbf {v} \ cdot \ mathbf {w}}.}$${\ displaystyle \ mu}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle {\ widehat {\ mu}} = (2 \ pi)^{-n} \ mu}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle {\ widehat {\ mu}}}$${\ displaystyle \ mu}$

${\ displaystyle {\ begin {align} \ mu & = (2 \ pi)^{-{\ frac {n} {2}}} \ times {\ text {Lebesgue-måling}} \\ {\ widehat {\ mu }} & = (2 \ pi)^{-{\ frac {n} {2}}} \ gange {\ tekst {Lebesgue-måling}} \ slut {justeret}}}$

Men hvis vi ændrer den måde, vi identificerer os med dens dobbelte gruppe, ved at bruge parringen ${\ displaystyle \ mathbb {R} ^{n}}$

${\ displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e^{2 \ pi i \ mathbf {v} \ cdot \ mathbf {w}},}$

så er Lebesgue -måling på lig med sin egen dobbeltmåling . Denne konvention minimerer antallet af faktorer, der viser sig forskellige steder, når Fourier -transformer eller inverse Fourier -transformer beregnes på det euklidiske rum. (I virkeligheden begrænser det det eneste til eksponenten snarere end som en forfaktor uden for integraltegnet.) Bemærk, at valget af, hvordan man identificerer sig med sin dobbelte gruppe, påvirker betydningen af ​​udtrykket "selv-dobbelt funktion", som er en funktion, der er lig med sin egen Fourier-transformation: ved hjælp af den klassiske parring er funktionen selv-dobbelt. Men at bruge parringen, som bevarer præfaktoren som enhed, gør i stedet sig selv-dobbelt. Denne anden definition for Fourier -transformen har den fordel, at den kortlægger den multiplikative identitet til konvolutionsidentiteten, hvilket er nyttigt ligesom en konvolutionsalgebra. Se det næste afsnit om gruppealgebraen . Desuden er denne form også nødvendigvis isometrisk på mellemrum. Se nedenfor ved Plancherel og L ² Fourier inversion sætninger${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle 2 \ pi}$${\ displaystyle 2 \ pi}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e^{i \ mathbf {v} \ cdot \ mathbf {w}}}$${\ displaystyle e^{-{\ frac {1} {2}} x^{2}}}$${\ displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e^{2 \ pi {i} {\ mathbf {v}} \ cdot {\ mathbf {w}}}}$${\ displaystyle e^{-\ pi x^{2}}}$${\ displaystyle L^{1}}$${\ displaystyle L^{2}}$

Gruppen algebra

Rummet med integrerbare funktioner på en lokalt kompakt abelsk gruppe er en algebra , hvor multiplikation er konvolution: konvolutionen af ​​to integrerbare funktioner og defineres som ${\ displaystyle G}$${\ displaystyle f}$${\ displaystyle g}$

${\ displaystyle (f*g) (x) = \ int _ {G} f (xy) g (y) \ d \ mu (y).}$

Sætning. Banach -rummet er en associativ og kommutativ algebra under konvolution.${\ displaystyle L^{1} (G)}$

Denne algebra kaldes gruppen Algebra for . Ved teoremet Fubini – Tonelli er konvolutionen submultiplicativ i forhold til normen og danner en Banach -algebra . Banach -algebraen har et multiplikativt identitetselement, hvis og kun hvis det er en diskret gruppe, nemlig den funktion, der er 1 ved identiteten og nul andre steder. Generelt har den imidlertid en omtrentlig identitet, som er en netto (eller generaliseret sekvens) indekseret på et rettet sæt, således at${\ displaystyle G}$${\ displaystyle L^{1}}$${\ displaystyle L^{1} (G)}$${\ displaystyle L^{1} (G)}$${\ displaystyle G}$${\ displaystyle \ {e_ {i} \} _ {i \ i I}}$${\ displaystyle I}$${\ displaystyle f*e_ {i} \ til f.}$

Fouriertransformen tager konvolution til multiplikation, dvs. det er en homomorfisme af abelske Banach -algebraer (af norm ≤ 1): ${\ displaystyle L^{1} (G) \ til C_ {0} \ venstre ({\ widehat {G}} \ højre)}$

${\ displaystyle {\ mathcal {F}} (f*g) (\ chi) = {\ mathcal {F}} (f) (\ chi) \ cdot {\ mathcal {F}} (g) (\ chi) .}$

Især for hvert gruppetegn på svarer en unik multiplikativ lineær funktionel til gruppealgebra defineret af ${\ displaystyle G}$

${\ displaystyle f \ mapsto {\ widehat {f}} (\ chi).}$

Det er en vigtig egenskab ved gruppealgebraen, at disse udtømmer sæt af ikke-trivielle (det vil sige ikke identisk nul) multiplikative lineære funktionaliteter på gruppealgebraen; se afsnit 34 i ( Loomis 1953 ). Det betyder, at Fourier -transformationen er et specielt tilfælde af Gelfand -transformationen .

Plancherel og L ² Fourier inversion sætninger

Som vi har angivet, er den dobbelte gruppe af en lokalt kompakt abelsk gruppe en lokalt kompakt abelsk gruppe i sig selv og har således en Haar-foranstaltning, eller mere præcist en hel familie af skala-relaterede Haar-foranstaltninger.

Sætning. Vælg en Haar -måling på, og lad være den dobbelte måling på som defineret ovenfor. Hvis er kontinuerlig med kompakt støtte så og ${\ displaystyle \ mu}$${\ displaystyle G}$${\ displaystyle \ nu}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle f: G \ til \ mathbb {C}}$${\ displaystyle {\ widehat {f}} \ i L^{2} \ venstre ({\ widehat {G}} \ højre)}$

${\ displaystyle \ int _ {G} | f (x) |^{2} \ d \ mu (x) = \ int _ {\ widehat {G}} \ venstre | {\ widehat {f}} (\ chi ) \ right |^{2} \ d \ nu (\ chi).}$

Især Fourier -transformationen er en isometri fra de komplekse værdiansatte kontinuerlige funktioner af kompakt support til -funktionerne på (ved hjælp af -normen med hensyn til μ for funktioner på og -normen med hensyn til ν for funktioner på ).${\ displaystyle L^{2}}$${\ displaystyle G}$${\ displaystyle L^{2}}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle L^{2}}$${\ displaystyle G}$${\ displaystyle L^{2}}$${\ displaystyle {\ widehat {G}}}$

Da de komplekse værdifulde kontinuerlige funktioner med kompakt support på er -tætte, er der en unik forlængelse af Fourier -transformen fra dette rum til en enhedsoperatør${\ displaystyle G}$${\ displaystyle L^{2}}$

${\ displaystyle {\ mathcal {F}}: L _ {\ mu}^{2} (G) \ til L _ {\ nu}^{2} \ venstre ({\ widehat {G}} \ højre).}$

og vi har formlen

${\ displaystyle \ forall f \ i L^{2} (G): \ quad \ int _ {G} | f (x) |^{2} \ d \ mu (x) = \ int _ {\ widehat { G}} \ venstre | {\ widehat {f}} (\ chi) \ højre |^{2} \ d \ nu (\ chi).}$

Bemærk, at for ikke -kompakte lokalt kompakte grupper indeholder rummet ikke , så Fourier -transformen af ​​generelle funktioner på er "ikke" givet af nogen form for integrationsformel (eller egentlig nogen eksplicit formel). For at definere Fourier -transformationen skal man ty til et teknisk trick som at starte på et tæt underrum som de kontinuerlige funktioner med kompakt understøttelse og derefter udvide isometrien med kontinuitet til hele rummet. Denne enhedsforlængelse af Fourier -transformen er det, vi mener med Fouriertransformen på pladsen med firkantede integrerbare funktioner. ${\ displaystyle G}$${\ displaystyle L^{1} (G)}$${\ displaystyle L^{2} (G)}$${\ displaystyle L^{2}}$${\ displaystyle G}$${\ displaystyle L^{2}}$

Dobbeltgruppen har også en omvendt Fourier -transformation i sig selv; den kan karakteriseres som den omvendte (eller tilstødende, da den er enhed) af Fouriertransformen. Dette er indholdet af Fourier -inversionsformlen, der følger. ${\ displaystyle L^{2}}$${\ displaystyle L^{2}}$

Sætning. Tilstødet til Fourier -transformationen, der er begrænset til kontinuerlige funktioner i kompakt understøttelse, er den inverse Fourier -transform

${\ displaystyle L _ {\ nu}^{2} \ venstre ({\ widehat {G}} \ højre) \ til L _ {\ mu}^{2} (G)}$

hvor er den dobbelte foranstaltning til .${\ displaystyle \ nu}$${\ displaystyle \ mu}$

I tilfælde er dobbeltgruppen naturligt isomorf for gruppen af ​​heltal, og Fouriertransformen er specialiseret til beregning af koefficienter for Fourierserier af periodiske funktioner. ${\ displaystyle G = \ mathbb {T}}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle \ mathbb {Z}}$

Hvis er en begrænset gruppe, genopretter vi den diskrete Fourier -transformation . Bemærk, at denne sag er meget let at bevise direkte. ${\ displaystyle G}$

Bohr-komprimering og næsten periodicitet

En vigtig anvendelse af Pontryagin -dualitet er følgende karakterisering af kompakte abelske topologiske grupper:

Sætning . En lokalt kompakt abelsk gruppe er kompakt, hvis og kun hvis den dobbelte gruppe er diskret. Omvendt er diskret, hvis og kun hvis den er kompakt.${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$

At det at være kompakt indebærer er diskret, eller det at være diskret indebærer, at det er kompakt, er en elementær konsekvens af definitionen af ​​den kompakt-åbne topologi på og behøver ikke Pontryagin-dualitet. Man bruger Pontryagin -dualitet til at bevise konversationerne. ${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle {\ widehat {G}}}$

Den Bohr sammenkrølningen er defineret for enhver topologisk gruppe , uanset om lokalt kompakt eller abelsk. En brug af Pontryagin -dualitet mellem kompakte abelske grupper og diskrete abelske grupper er at karakterisere Bohr -komprimeringen af ​​en vilkårlig abelsk lokalt kompakt topologisk gruppe. Den Bohr sammenkrølningen af er , hvor H har gruppen struktur , men i betragtning af den diskrete topologi . Siden inklusionskortet${\ displaystyle G}$${\ displaystyle G}$ ${\ displaystyle B (G)}$${\ displaystyle G}$${\ displaystyle {\ widehat {H}}}$${\ displaystyle {\ widehat {G}}}$

${\ displaystyle \ iota: H \ til {\ widehat {G}}}$

er kontinuerlig og en homomorfisme, den dobbelte morfisme

${\ displaystyle G \ sim {\ widehat {\ widehat {G}}} \ til {\ widehat {H}}}$

er en morfisme til en kompakt gruppe, som let kan vise sig at opfylde den nødvendige universelle ejendom .

Se også næsten periodisk funktion .

Kategoriske overvejelser

Pontryagin -dualitet kan også rentabelt betragtes funktionelt . I det følgende LCA er kategori af lokalt kompakte abelian grupper og kontinuerlige gruppehomomorfi. Den dobbelte gruppe opførelse af en kontravariant functor LCA → LCA , repræsenteret (i betydningen repræsenterbare functors ) af cirklen gruppe som Især dobbelt dual functor er covariant . En kategorisk formulering af Pontryagin -dualitet siger derefter, at den naturlige transformation mellem identitetsfunktoren på LCA og den dobbelte dobbelte funktor er en isomorfisme. Ved at afvikle forestillingen om en naturlig transformation betyder det, at kortene er isomorfier for enhver lokalt kompakt abelsk gruppe , og disse isomorfier er funktionsmæssige i . Denne isomorfisme er analog med den dobbelte dobbelte af endelige-dimensionelle vektorrum (et specielt tilfælde for reelle og komplekse vektorrum). ${\ displaystyle {\ widehat {G}}}$${\ displaystyle \ mathbb {T}}$${\ displaystyle {\ widehat {G}} = {\ text {Hom}} (G, \ mathbb {T}).}$${\ displaystyle G \ til {\ widehat {\ widehat {G}}}}$${\ displaystyle G \ til \ operatorname {Hom} (\ operatorname {Hom} (G, T), T)}$${\ displaystyle G}$${\ displaystyle G}$

En umiddelbar konsekvens af denne formulering er en anden almindelig kategorisk formulering af Pontryagin -dualitet: dobbeltgruppefunktoren er en ækvivalens af kategorier fra LCA til LCA ^op .

Dualiteten udveksler underkategorierne for diskrete grupper og kompakte grupper . Hvis er en ring og er et venstre - modul , bliver dobbeltgruppen et højre - modul; på denne måde kan vi også se, at diskrete venstre - moduler vil være Pontryagin dobbelt til kompakte højre - moduler. Ringen af endomorfismer i LCA ændres ved dualitet til dens modsatte ring (ændr multiplikationen til den anden rækkefølge). For eksempel, hvis er en uendelig cyklisk diskret gruppe, er en cirkelgruppe: førstnævnte har, så dette er sandt også for sidstnævnte. ${\ displaystyle R}$${\ displaystyle G}$${\ displaystyle R}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle R}$${\ displaystyle R}$${\ displaystyle R}$${\ displaystyle {\ text {End}} (G)}$${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle {\ text {End}} (G) = \ mathbb {Z}}$

Generaliseringer

Generaliseringer af Pontryagin -dualitet er konstrueret i to hovedretninger: for kommutative topologiske grupper , der ikke er lokalt kompakte , og for ikke -kommutative topologiske grupper. Teorierne i disse to sager er meget forskellige.

Dualiteter for kommutative topologiske grupper

Hvornår er en Hausdorff abelsk topologisk gruppe, gruppen med den kompakte åbne topologi er en Hausdorff abelsk topologisk gruppe og den naturlige kortlægning fra til dens dobbelt-dual giver mening. Hvis denne kortlægning er en isomorfisme, siges det, at tilfredsstiller Pontryagin -dualitet (eller det er en refleksiv gruppe eller en reflekterende gruppe ). Dette er blevet udvidet i en række retninger ud over den sag, der er lokalt kompakt. ${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle G}$${\ displaystyle {\ widehat {\ widehat {G}}}}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$

Især viste Samuel Kaplan i 1948 og 1950, at vilkårlige produkter og utallige omvendte grænser for lokalt kompakte (Hausdorff) abelske grupper tilfredsstiller Pontryagins dualitet. Bemærk, at et uendeligt produkt af lokalt kompakte ikke-kompakte rum ikke er lokalt kompakt.

Senere, i 1975, viste Rangachari Venkataraman blandt andet, at hver åben undergruppe af en abelsk topologisk gruppe, der tilfredsstiller Pontryagin -dualiteten i sig selv, tilfredsstiller Pontryagins dualitet.

For nylig har Sergio Ardanza-Trevijano og María Jesús Chasco forlænget resultaterne af Kaplan nævnt ovenfor. De viste, at direkte og omvendte grænser for sekvenser af abelske grupper, der tilfredsstiller Pontryagin -dualitet, også tilfredsstiller Pontryagin -dualitet, hvis grupperne er metrerbare eller -rum, men ikke nødvendigvis lokalt kompakte, forudsat at nogle ekstra betingelser er opfyldt af sekvenserne. ${\ displaystyle k _ {\ omega}}$

Der er imidlertid et grundlæggende aspekt, der ændrer sig, hvis vi vil overveje Pontryagin -dualitet ud over den lokalt kompakte sag. Elena Martín-Peinador beviste i 1995, at if er en Hausdorff abelsk topologisk gruppe, der tilfredsstiller Pontryagins dualitet og den naturlige evalueringsparring ${\ displaystyle G}$

${\ displaystyle {\ begin {cases} G \ times {\ widehat {G}} \ to \ mathbb {T} \\ (x, \ chi) \ mapsto \ chi (x) \ end {cases}}}$

er (i fællesskab) kontinuerlig, så er den lokalt kompakt. Som en følge heraf er alle ikke-lokalt kompakte eksempler på Pontryagin-dualitet grupper, hvor parringen ikke (i fællesskab) er kontinuerlig. ${\ displaystyle G}$${\ displaystyle G \ times {\ widehat {G}} \ to \ mathbb {T}}$

En anden måde at generalisere Pontryagin -dualitet til bredere klasser af kommutative topologiske grupper er at skænke dobbeltgruppen en lidt anden topologi, nemlig topologien for ensartet konvergens på totalt afgrænsede sæt . Grupperne, der opfylder identiteten under denne antagelse, kaldes stereotype grupper . Denne klasse er også meget bred (og den indeholder lokalt kompakte abelske grupper), men den er smallere end klassen af ​​reflekterende grupper. ${\ displaystyle {\ widehat {G}}}$${\ displaystyle G \ cong {\ widehat {\ widehat {G}}}}$

Pontryagin dualitet for topologiske vektorrum

I 1952 lagde Marianne F. Smith mærke til, at Banach -rum og refleksive rum , der betragtes som topologiske grupper (med additivgruppeoperationen), tilfredsstiller Pontryagin -dualitet. Senere viste BS Brudovskiĭ, William C. Waterhouse og K. Brauner, at dette resultat kan udvides til at omfatte alle kvasi-komplette tønderum (især til alle Fréchet-rum ). I 1990'erne gav Sergei Akbarov en beskrivelse af klassen af ​​de topologiske vektorrum, der tilfredsstiller en stærkere egenskab end den klassiske Pontryagin -refleksivitet, nemlig identiteten

${\ displaystyle (X^{\ star})^{\ star} \ cong X}$

hvor betyder rummet for alle lineære kontinuerlige funktionaliteter udstyret med topologien om ensartet konvergens på totalt afgrænsede sæt i (og betyder det dobbelte til i samme forstand). Rummene i denne klasse kaldes stereotype rum , og den tilsvarende teori fandt en række anvendelser inden for funktionsanalyse og geometri, herunder generalisering af Pontryagin-dualitet for ikke-kommutative topologiske grupper. ${\ displaystyle X^{\ star}}$${\ displaystyle f \ kolon X \ til {\ mathbb {C}}}$${\ displaystyle X}$${\ displaystyle (X^{\ star})^{\ star}}$${\ displaystyle X^{\ star}}$

Dualiteter for ikke-kommutative topologiske grupper

For ikke-kommutative lokalt kompakte grupper holder den klassiske Pontryagin-konstruktion op med at arbejde af forskellige årsager, især fordi tegnene ikke altid adskiller punkterne i , og de ureducerbare repræsentationer af ikke altid er endimensionelle. På samme tid er det ikke klart, hvordan man introducerer multiplikation på sættet med ureducerbare enhedsrepræsentationer af , og det er endda ikke klart, om dette sæt er et godt valg til rollen som det dobbelte objekt for . Så problemet med at konstruere dualitet i denne situation kræver fuldstændig nytænkning. ${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$

Teorier, der er bygget til dato, er opdelt i to hovedgrupper: teorier, hvor det dobbelte objekt har samme natur som den oprindelige (som i selve Pontryagin -dualiteten), og teorierne, hvor kildeobjektet og dets dual adskiller sig så radikalt fra hinanden at det er umuligt at tælle dem som objekter i en klasse.

Den anden type teori var historisk den første: kort tid efter Pontryagins arbejde konstruerede Tadao Tannaka (1938) og Mark Kerin (1949) en dualitetsteori for vilkårlige kompakte grupper kendt nu som Tannaka - Kerin -dualiteten . I denne teori er det dobbelte objekt for en gruppe ikke en gruppe, men en kategori af dens repræsentationer . ${\ displaystyle G}$ ${\ displaystyle \ Pi (G)}$

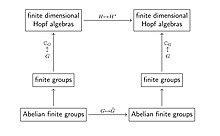
Teorierne om den første type dukkede op senere, og nøgleeksemplet for dem var dualitetsteorien for begrænsede grupper. I denne teori er kategorien af ​​begrænsede grupper indlejret ved operationen med at tage gruppealgebra (over ) ind i kategorien af ​​endelige dimensionelle Hopf -algebraer , så Pontryagin -dualitetsfunktoren bliver til driften af at tage det dobbelte vektorrum (hvilket er en dualitet functor i kategorien endelige dimensionelle Hopf -algebraer). ${\ displaystyle G \ mapsto {\ mathbb {C}} _ ​​{G}}$ ${\ displaystyle {\ mathbb {C}} _ ​​{G}}$${\ displaystyle {\ mathbb {C}}}$${\ displaystyle G \ mapsto {\ widehat {G}}}$${\ displaystyle H \ mapsto H^{*}}$

I 1973 Leonid I. Vainerman, George I. Kac, Michel Enock og Jean-Marie Schwartz byggede en generel teori af denne type for alle lokalt kompakte grupper. Fra 1980'erne blev forskningen på dette område genoptaget efter opdagelsen af kvantegrupper , hvortil de konstruerede teorier begyndte at blive aktivt overført. Disse teorier er formuleret i sproget for C*-algebraer eller Von Neumann-algebraer , og en af ​​dens varianter er den nylige teori om lokalt kompakte kvantegrupper .

En af ulemperne ved disse generelle teorier er imidlertid, at de objekter, der generaliserer begrebet gruppe, ikke er Hopf -algebraer i den sædvanlige algebraiske forstand. Denne mangel kan korrigeres (for nogle grupper af grupper) inden for rammerne af dualitetsteorier konstrueret på grundlag af forestillingen om konvolut af topologisk algebra.

Se også

• Peter – Weyl sætning
• Cartier dualitet
• Stereotype rum

Noter

Referencer

• Dixmier, Jacques (1969). Les C*-algèbres et leurs Représentations . Gauthier-Villars. ISBN 978-2-87647-013-2.
• Enock, Michel; Schwartz, Jean-Marie (1992). Kac -algebraer og dualitet af lokalt kompakte grupper . Med et forord af Alain Connes. Med en postface af Adrian Ocneanu. Berlin: Springer-Verlag. doi : 10.1007/978-3-662-02813-1 . ISBN 978-3-540-54745-7. MR  1215933 .
• Hewitt, Edwin; Ross, Kenneth A. (1963). Abstrakt harmonisk analyse. Vol. I: Struktur af topologiske grupper. Integrationsteori, gruppeforestillinger . Die Grundlehren der mathematatischen Wissenschaften. 115 . Berlin-Göttingen-Heidelberg: Springer-Verlag. ISBN 978-0-387-94190-5. MR  0156915 .
• Hewitt, Edwin; Ross, Kenneth A. (1970). Abstrakt harmonisk analyse . 2 . ISBN 978-3-662-24595-8. MR  0262773 .
• Kirillov, Alexandre A. (1976) [1972]. Elementer i teorien om repræsentationer . Grundlehren der Mathematischen Wissenschaften. 220 . Berlin, New York: Springer-Verlag . ISBN 978-0-387-07476-4. MR  0412321 .
• Loomis, Lynn H. (1953). En introduktion til abstrakt harmonisk analyse . D. van Nostrand Co. ISBN 978-0486481234.
• Morris, SA (1977). Pontryagin -dualitet og strukturen i lokalt kompakte abelske grupper . Cambridge University Press . ISBN 978-0521215435.
• Onishchik, AL (1984). Pontrjagin dualitet . Matematikens encyklopædi . 4 . s. 481–482. ISBN 978-1402006098.
• Reiter, Hans (1968). Klassisk harmonisk analyse og lokalt kompakte grupper . ISBN 978-0198511892.
• Rudin, Walter (1962). Fourier -analyse af grupper . D. van Nostrand Co. ISBN 978-0471523642.
• Timmermann, T. (2008). En invitation til kvantegrupper og dualitet - fra Hopf -algebraer til multiplikative enheder og videre . EMS Lærebøger i matematik, European Mathematical Society. ISBN 978-3-03719-043-2.
• Kustermans, J .; Vaes, S. (2000). "Lokalt kompakte kvantegrupper" . Annales Scientifiques de l'École Normale Supérieure . 33 (6): 837–934. doi : 10.1016/s0012-9593 (00) 01055-7 .
• Ardanza-Trevijano, Sergio; Chasco, María Jesús (2005). "Pontryagin -dualiteten af ​​sekventielle grænser for topologiske abelske grupper". Journal of Pure and Applied Algebra . 202 (1–3): 11–21. doi : 10.1016/j.jpaa.2005.02.006 . HDL : 10171/1586 . MR  2163398 .
• Chasco, María Jesús; Dikranjan, Dikran; Martín-Peinador, Elena (2012). "En undersøgelse om refleksivitet af abelske topologiske grupper" . Topologi og dens anvendelser . 159 (9): 2290–2309. doi : 10.1016/j.topol.2012.04.012 . MR  2921819 .
• Kaplan, Samuel (1948). "Udvidelser af Pontrjagin -dualiteten. Del I: uendelige produkter". Duke Mathematical Journal . 15 : 649–658. doi : 10.1215/S0012-7094-48-01557-9 . MR  0026999 .
• Kaplan, Samuel (1950). "Udvidelser af Pontrjagin -dualiteten. Del II: direkte og omvendte grænser". Duke Mathematical Journal . 17 : 419–435. doi : 10.1215/S0012-7094-50-01737-6 . MR  0049906 .
• Venkataraman, Rangachari (1975). "Udvidelser af Pontryagin Duality". Mathematische Zeitschrift . 143 (2): 105–112. doi : 10.1007/BF01187051 . S2CID  123627326 .
• Martin-Peinador, Elena (1995). "En refleksibel, acceptabel topologisk gruppe skal være lokalt kompakt". Proceedings of the American Mathematical Society . 123 (11): 3563–3566. doi : 10.2307/2161108 . HDL : 10338.dmlcz / 127.641 . JSTOR  2161108 .
• Smith, Marianne F. (1952). "Pontrjagin -dualitetsteoremet i lineære rum". Annals of Mathematics . 56 (2): 248–253. doi : 10.2307/1969798 . JSTOR  1969798 . MR  0049479 .
• Brudovskiĭ, BS (1967). "Om k- og c-refleksivitet af lokalt konvekse vektorrum". Litauisk matematisk tidsskrift . 7 (1): 17–21.
• Waterhouse, William C. (1968). "Doble grupper af vektorrum" . Pacific Journal of Mathematics . 26 (1): 193–196. doi : 10.2140/pjm.1968.26.193 .
• Brauner, Kalman (1973). "Dualer af Fréchet -rum og en generalisering af Banach - Dieudonné -sætningen". Duke Mathematical Journal . 40 (4): 845–855. doi : 10.1215/S0012-7094-73-04078-7 .
• Akbarov, SS (2003). "Pontryagin -dualitet i teorien om topologiske vektorrum og i topologisk algebra". Journal of Mathematical Sciences . 113 (2): 179–349. doi : 10.1023/A: 1020929201133 . S2CID  115297067 .
• Akbarov, Sergei S .; Shavgulidze, Evgeniy T. (2003). "På to klasser af rum refleksive i betydningen Pontryagin" . Matematicheskii Sbornik . 194 (10): 3–26.
• Akbarov, Sergei S. (2009). "Holomorfe funktioner af eksponentiel type og dualitet for Stein -grupper med algebraisk forbundet identitetskomponent". Journal of Mathematical Sciences . 162 (4): 459–586. arXiv : 0806.3205 . doi : 10.1007/s10958-009-9646-1 . S2CID  115153766 .
• Akbarov, Sergei S. (2017). "Kontinuerlige og glatte konvolutter af topologiske algebraer. Del 1". Journal of Mathematical Sciences . 227 (5): 531–668. arXiv : 1303.2424 . doi : 10.1007/s10958-017-3599-6 . MR  3790317 . S2CID  126018582 .
• Akbarov, Sergei S. (2017). "Kontinuerlige og glatte konvolutter af topologiske algebraer. Del 2". Journal of Mathematical Sciences . 227 (6): 669–789. arXiv : 1303.2424 . doi : 10.1007/s10958-017-3600-4 . MR  3796205 . S2CID  128246373 .