Dualitet (matematik) - Duality (mathematics)

I matematik oversætter en dualitet begreber, sætninger eller matematiske strukturer til andre begreber, sætninger eller strukturer, på en-til-en måde, ofte (men ikke altid) ved hjælp af en involutionsoperation : hvis dobbeltværdien af A er B , derefter den dobbelte af B er A . Sådanne involveringer har undertiden faste punkter , så dualiteten af A er A selv. For eksempel Desargues' teorem er selv-dual i denne forstand under den standard dobbelthed i Projektiv geometri .

I matematiske sammenhænge har dualitet adskillige betydninger. Det er blevet beskrevet som "et meget gennemgribende og vigtigt begreb i (moderne) matematik" og "et vigtigt generelt tema, der har manifestationer på næsten alle områder af matematik".

Mange matematiske dualiteter mellem objekter af to typer svarer til parringer , bilineære funktioner fra et objekt af en type og et andet objekt af den anden type til en eller anden familie af skalarer. For eksempel svarer lineær algebra-dualitet på denne måde til bilineære kort fra par af vektorrum til skalarer, dualiteten mellem distributioner og de tilknyttede testfunktioner svarer til parringen, hvor man integrerer en fordeling mod en testfunktion, og Poincaré-dualitet svarer på samme måde til skæringsnummer , set på som et parring mellem submanifolds af en given manifold.

Fra et kategoritetorisk synspunkt kan dualitet også ses som en funktor , i det mindste inden for vektorrum. This functor tildeler hvert rum dets dobbelte plads og tilbagetrækning byggeri tildeler hver pil f : V → W sin dobbelte f ^* : W ^* → V ^* .

Indledende eksempler

Med ordene fra Michael Atiyah ,

Dualitet i matematik er ikke en sætning, men et "princip".

Den følgende liste med eksempler viser de fælles træk ved mange dualiteter, men indikerer også, at den nøjagtige betydning af dualitet kan variere fra sag til sag.

Supplering af en delmængde

En enkel, måske den mest enkle, opstår dualitet fra at overveje delmængder af et fast sæt S . Ethvert delmængde A ⊆ S , den komplementet A ^c består af alle de elementer i S , som ikke er indeholdt i A . Det er igen en delmængde af S . At tage komplementet har følgende egenskaber:

• Anvendelse af det to gange giver tilbage det oprindelige sæt, dvs. ( A ^c ) ^c = A . Dette henvises til ved at sige, at operationen med at tage komplementet er en involution .
• En inklusion af sæt A ⊆ B omdannes til en inklusion i den modsatte retning B ^c ⊆ A ^c .
• Givet to undergrupper A og B af S , er A indeholdt i B ^c, hvis og kun hvis B er indeholdt i A ^c .

Denne dualitet vises i topologi som en dualitet mellem åbne og lukkede undergrupper af et eller andet fast topologisk rum X : et undersæt U af X lukkes, hvis og kun hvis dets komplement i X er åbent. På grund af dette er mange sætninger om lukkede sæt dobbelte med sætninger om åbne sæt. For eksempel er enhver forening af åbne sæt åben, så dobbelt er ethvert kryds mellem lukkede sæt lukket. Det indre af et sæt er det største åbne sæt indeholdt i det, og lukningen af sættet er det mindste lukkede sæt, der indeholder det. På grund af den dobbelthed, komplementet af det indre af et sæt U er lig med lukningen af komplementet af U .

Dobbelt kegle

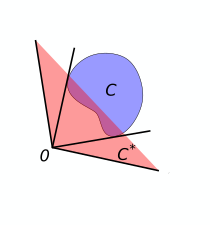
En dualitet i geometri tilvejebringes af den dobbelte keglekonstruktion . Givet et sæt punkter i planet (eller mere generelt punkter ind ) defineres dobbeltkeglen som det sæt, der består af de punkter, der tilfredsstiller ${\ displaystyle C}$${\ displaystyle \ mathbb {R} ^ {2}}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle C ^ {*} \ subseteq \ mathbb {R} ^ {2}}$${\ displaystyle (x_ {1}, x_ {2})}$

for alle punkter i , som illustreret i diagrammet. I modsætning til komplementet af sæt nævnt ovenfor er det generelt ikke sandt, at anvendelse af dobbeltkeglekonstruktionen to gange giver det originale sæt tilbage . I stedet er den mindste kegle, der kan være større end . Derfor er denne dualitet svagere end den ovenfor, i det ${\ displaystyle (c_ {1}, c_ {2})}$${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle C ^ {**}}$${\ displaystyle C}$${\ displaystyle C}$

• Anvendelse af operationen to gange giver tilbage et eventuelt større sæt: for alle , der er indeholdt i . (For nogle , nemlig keglerne, er de to lige store.) ${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle C ^ {**}}$${\ displaystyle C}$

De to andre egenskaber overføres uden ændringer:

• Det er stadig sandt, at en inklusion bliver til en inklusion i den modsatte retning ( ). ${\ displaystyle C \ subseteq D}$${\ displaystyle D ^ {*} \ subseteq C ^ {*}}$
• Givet to delmængder og af flyet, er indeholdt i hvis og kun hvis er indeholdt i . ${\ displaystyle C}$${\ displaystyle D}$${\ displaystyle C}$${\ displaystyle D ^ {*}}$${\ displaystyle D}$${\ displaystyle C ^ {*}}$

Dobbelt vektorrum

Et meget vigtigt eksempel på en dualitet opstår i lineær algebra ved at tilknytte ethvert vektorrum V dets dobbelte vektorrum V ^* . Dets elementer er de lineære funktionaliteter , hvor k er det felt, hvor V er defineret. De tre egenskaber af den dobbelte kegle overføres til denne type dualitet ved at erstatte delmængder af med vektorrum og indeslutninger af sådanne delmængder med lineære kort. Det er: ${\ displaystyle \ varphi: V \ til k}$${\ displaystyle \ mathbb {R} ^ {2}}$

• Anvendelse af operationen med at tage det dobbelte vektorrum to gange giver et andet vektorrum V ^** . Der er altid et kort V → V ^** . For nogle V , nemlig nøjagtigt de endelige-dimensionelle vektorrum , er dette kort en isomorfisme .
• Et lineært kort V → W giver anledning til et kort i den modsatte retning ( W ^* → V ^* ).
• Givet to vektorrum V og W , svarer kortene fra V til W ^* til kortene fra W til V ^* .

Et særligt træk ved denne dualitet er, at V og V ^* er isomorfe for bestemte objekter, nemlig endelige-dimensionelle vektorrum. Dette er imidlertid i en vis forstand en heldigt sammentræf, for at give en sådan isomorfi kræver en vis valg, fx valget af en basis af V . Dette gælder også i tilfældet, hvis V er en Hilbert rum , via den Riesz repræsentation teorem .

Galois teori

I alle de dualiteter, der er diskuteret før, er det dobbelte af et objekt af samme art som selve objektet. For eksempel er det dobbelte af et vektorrum igen et vektorrum. Mange dualitetserklæringer er ikke af denne art. I stedet for afslører sådanne dualiteter en tæt sammenhæng mellem objekter af tilsyneladende forskellig art. Et eksempel på en sådan mere generel dualitet er fra Galois-teorien . For en fast Galois-udvidelse K / F kan man knytte Galois-gruppen Gal ( K / E ) til ethvert mellemfelt E (dvs. F ⊆ E ⊆ K ). Denne gruppe er en undergruppe af Galois-gruppen G = Gal ( K / F ) . Omvendt til en sådan undergruppe H ⊆ G er den faste felt K ^H bestående af elementer fastsat ved elementerne i H .

Sammenlignet med ovenstående har denne dualitet følgende funktioner:

• En udvidelse F ⊆ F ′ af mellemliggende felter giver anledning til en inkludering af Galois-grupper i den modsatte retning: Gal ( K / F ′) ⊆ Gal ( K / F ) .
• Tilknytning af Gal ( K / E ) til E og K ^H til H er omvendte af hinanden. Dette er indholdet af Galois-teoriens grundlæggende sætning .

Ordrevendende dualiteter

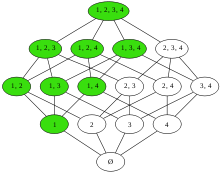
Givet en poset P = ( X , ≤) (kort for delvist ordnet sæt, altså et sæt, der har en begrebet bestilling men hvori to elementer ikke nødvendigvis kan placeres i rækkefølge i forhold til hinanden), den dobbelte poset P ^d = ( X , ≥) omfatter det samme grundsæt, men det omvendte forhold . Kendte eksempler på dobbelt delordrer inkluderer

• delmængden og overmængde forbindelser ⊂ og ⊃ på enhver samling af sæt, såsom delmængder af et fast sæt S . Dette giver anledning til det første eksempel på en dualitet nævnt ovenfor .
• de kløfter og flere af relationer på de tal .
• den efterkommer-af og forfader-af relationer på det sæt af mennesker.

En dobbelthed transformation er en involutive antiautomorphism f af et delvist ordnet sæt S , dvs. en ordre-reverserende involution f  : S → S . I flere vigtige tilfælde bestemmer disse enkle egenskaber transformationen entydigt op til nogle enkle symmetrier. For eksempel, hvis f ₁ , f ₂ er to dobbelthed transformationer så deres sammensætning er en ordre automorfi af S ; således adskiller enhver to dualitetstransformationer sig kun ved en ordreautomorfisme. For eksempel er alle ordens automorphisms af en strøm sæt S = 2 ^R induceres af permutationer af R .

Et koncept defineret for en delvis ordre P vil svare til en dobbelt koncept på den dobbelte poset P ^d . For eksempel, en minimal del af P vil være en maksimal element af P ^d : minimality og maksimalitet er dobbelt begreber med henblik på teori. Andre par dobbelte begreber er øvre og nedre grænser , nedre sæt og øvre sæt og idealer og filtre .

I topologi er åbne sæt og lukkede sæt to begreber: komplementet til et åbent sæt er lukket og omvendt. I matroidteori danner familien af ​​sæt, der supplerer de uafhængige sæt af en given matroid, selv en anden matroid, kaldet dual matroid .

Dimensionsomvendte dualiteter

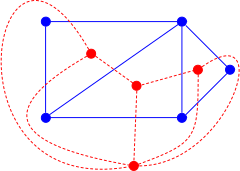
Der er mange forskellige, men indbyrdes forbundne dualiteter, hvor geometriske eller topologiske objekter svarer til andre objekter af samme type, men med en vending af dimensionerne af objekternes egenskaber. Et klassisk eksempel på dette er dualiteten af ​​de platoniske faste stoffer , hvor kuben og oktaederne danner et dobbelt par, dodekaeder og ikosaeder danner et dobbelt par, og tetraedret er selvdobbelt. Den dobbelte polyhedron af en hvilken som helst af disse polyhedre kan dannes som det konvekse skrog af midterpunkterne på hver overflade af den primære polyhedron, så toppunkterne i den dobbelte svarer en-til-en med ansigterne på den primære. Tilsvarende svarer hver kant af den dobbelte til en kant af den primære, og hver side af den dobbelte svarer til en toppunkt af den primære. Disse korrespondancer er incidensbevarende: hvis to dele af den primære polyhedron rører hinanden, så gør de tilsvarende to dele af den dobbelte polyhedron det også . Mere generelt svarer enhver konveks polyhedron eller mere generelt enhver konveks polytop med begrebet polær reciprocation til en dobbelt polyhedron eller dobbelt polytop med et i- dimensionelt træk ved en n- dimensionel polytop svarende til en ( n - i - 1) -dimensionelt træk ved den dobbelte polytop. Den forekomstbevarende karakter af dualiteten afspejles i det faktum, at ansigtsgitterene i de primære og dobbelte polyedre eller polytoper i sig selv er ordensteoretiske dualer . Dualitet af polytoper og orden-teoretisk dualitet er begge involveringer : den dobbelte polytop af den dobbelte polytop af enhver polytop er den oprindelige polytop, og at vende alle orden-forhold to gange vender tilbage til den oprindelige rækkefølge. At vælge et andet polaritetscenter fører til geometrisk forskellige dobbelte polytoper, men alle har den samme kombinatoriske struktur.

Fra en hvilken som helst tredimensionel polyhedron kan man danne en plan graf , grafen over dens hjørner og kanter. Den dobbelte polyhedron har en dobbelt graf , en graf med et toppunkt for hver overflade af polyhedronen og med en kant for hver to tilstødende ansigter. Det samme koncept med plan graf dualitet kan generaliseres til grafer, der er tegnet i planet, men som ikke kommer fra en tredimensionel polyhedron, eller mere generelt til grafindlejringer på overflader af højere slægt: man kan tegne en dobbelt graf ved at placere et toppunkt inden for hver region afgrænset af en cyklus af kanter i indlejringen og tegner en kant, der forbinder to regioner, der deler en afgrænsningskant. Et vigtigt eksempel på denne type kommer fra beregningsmæssige geometri : dualiteten for enhver endelig mængde S af punkter i planet mellem Delaunay triangulering af S og Voronoi diagram af S . Som med dobbelt polyhedra og dobbelt polytoper er dualiteten af ​​grafer på overflader en dimension-omvendt involvering: hvert toppunkt i den oprindelige indlejrede graf svarer til en region af den dobbelte indlejring, hver kant i primalen krydses af en kant i den dobbelte , og hver region af primalen svarer til et toppunkt i det dobbelte. Den dobbelte graf afhænger af, hvordan den primære graf er indlejret: forskellige plane indlejringer af en enkelt graf kan føre til forskellige dobbelte grafer. Matroid dualitet er en algebraisk udvidelse af plan graf dualitet i den forstand, at den dobbelte matroid i den grafiske matroid i en plan graf er isomorf til den grafiske matroid i den dobbelte graf.

En slags geometrisk dualitet forekommer også i optimeringsteorien , men ikke en, der vender dimensioner. Et lineært program kan specificeres af et system med reelle variabler (koordinaterne for et punkt i det euklidiske rum ), et system med lineære begrænsninger (angive, at punktet ligger i et halvt rum ; skæringspunktet mellem disse halvrum er en konveks polytop, det mulige region af programmet) og en lineær funktion (hvad der skal optimeres). Hvert lineært program har et dobbelt problem med den samme optimale løsning, men variablerne i det dobbelte problem svarer til begrænsninger i det primære problem og omvendt. ${\ displaystyle \ mathbb {R} ^ {n}}$

Dualitet i logik og sætteori

I logik betragtes funktioner eller relationer A og B dobbelt, hvis A (¬ x ) = ¬ B ( x ) , hvor ¬ er logisk negation . Den grundlæggende dualitet af denne type er dualiteten af ​​∃ og ∀ kvantificeringsanordningerne i klassisk logik. Disse er dobbelte, fordi ∃ x .¬ P ( x ) og ¬∀ x . P ( x ) er ækvivalente for alle prædikater P i klassisk logik: hvis der findes et x, hvor P ikke holder, er det falsk, at P holder for alle x (men det omvendte holder ikke konstruktivt). Fra denne grundlæggende logiske dualitet følger flere andre:

• En formel siges at være tilfredsstillende i en bestemt model, hvis der er tildelinger til dens gratis variabler, der gør det sandt; det er gyldigt, hvis hver tildeling til dets gratis variabler gør det sandt. Tilfredshed og gyldighed er dobbelt, fordi de ugyldige formler er netop dem, hvis negationer er tilfredsstillende, og de utilstrækkelige formler er dem, hvis negationer er gyldige. Dette kan ses som et specielt tilfælde af det forrige element, hvor kvantificeringsværdierne spænder over fortolkninger.
• I klassisk logik er ∧ og ∨ operatorerne dobbelt i denne forstand, fordi (¬ x ∧ ¬ y ) og ¬ ( x ∨ y ) er ækvivalente. Dette betyder, at der for hver sætning af klassisk logik er en ækvivalent dobbelt sætning. De Morgans love er eksempler. Mere generelt er ∧ (¬ x _i ) = ¬ ∨ x _i . Venstre side er sand, hvis og kun hvis ∀ i .¬ x _i , og højre side hvis og kun hvis ¬∃ i . x _i .
• I modalogik betyder □ p , at propositionen p er "nødvendigvis" sand, og ◊ p at p er "muligvis" sand. De fleste fortolkninger af modalogik tildeler disse to operatører dobbelt betydning. For eksempel i Kripke semantik betyder " p muligvis sandt", "der findes en verden W sådan, at p er sandt i W ", mens " p nødvendigvis er sandt" betyder "for alle verdener W , p er sandt i W ". Dobbelthed □ og ◊ følger derefter fra den analoge dobbelthed af ∀ og ∃ . Andre dobbeltmodale operatører opfører sig på samme måde. For eksempel har timelogik operatører, der betegner "vil være sandt på et eller andet tidspunkt i fremtiden" og "vil være sandt til enhver tid i fremtiden", som er ligeledes dobbelt.

Andre analoge dualiteter følger af disse:

• Sæt-teoretisk union og skæringspunktet er dobbelt under indstillede komplement operatør ⋅ ^C . Det vil sige A ^C ∩ B ^C = ( A ∪ B ) ^C og mere generelt ∩ A ^C
  _α = ( ∪ A _α ) ^C . Dette følger af dualiteten mellem ∀ og ∃ : et element x er et medlem af ∩ A ^C
  _α hvis og kun hvis ∀ α .¬ x ∈ A _α , og er medlem af ( ∪ A _α ) ^C, hvis og kun hvis ¬∃ α . x ∈ A _α .

Dobbeltgenstande

En gruppe af dualiteter kan beskrives ved tilføre for enhver matematisk objekt X , sættet af morfier Hom ( X , D ) ind i nogle fast genstand D , med en struktur svarende til den af X . Dette kaldes undertiden intern Hom . Generelt giver dette en sand dualitet kun til bestemte valg af D , i hvilket tilfælde X ^* = Hom ( X , D ) betegnes som den dobbelte af X . Der er altid et kort fra X til bidualet , det vil sige det dobbelte af det dobbelte,

Det tildeler nogle x ∈ X kortet, der knytter sig til ethvert kort f  : X → D (dvs. et element i Hom ( X , D ) ) værdien f ( x ) . Afhængigt af den konkrete dualitet, der overvejes, og også afhængigt af objektet X , kan dette kort måske eller ikke være en isomorfisme.

Dobbelt vektorrum igen

Konstruktionen af ​​det dobbelte vektorrum

nævnt i indledningen er et eksempel på en sådan dualitet. Faktisk danner sættet af morfismer, dvs. lineære kort , et vektorrum i sig selv. Ovenstående kort V → V ^** er altid injektionsdygtigt. Det er overvejende og derfor en isomorfisme, hvis og kun hvis dimensionen af V er endelig. Denne kendsgerning karakteriserer endelige-dimensionelle vektorrum uden at henvise til et grundlag.

Isomorfier af V og V ^∗ og indre produktrum

Et vektorrum V er isomorft til V ^∗ netop hvis V er endelig-dimensionelt. I dette tilfælde svarer en sådan isomorfisme til en ikke-degenereret bilinær form

I dette tilfælde kaldes V et indre produktrum . For eksempel, hvis K er feltet med reelle eller komplekse tal , giver en hvilken som helst positiv bestemt bilinær form anledning til en sådan isomorfisme. I riemannsk geometri , V antages at være tangent plads af en manifold og sådanne positive bilineære former kaldes Riemannske metrics . Deres formål er at måle vinkler og afstande. Således er dualitet et grundlæggende grundlag for denne gren af ​​geometri. En anden anvendelse af indre produktrum er Hodge-stjernen, som giver en korrespondance mellem elementerne i den udvendige algebra . For et n -dimensionelt vektorrum kortlægger Hodge-stjerneoperatøren k -former til ( n - k ) -former. Dette kan bruges til at formulere Maxwells ligninger . I denne forklædning udveksler dualiteten i det indre produktrum rollen som magnetiske og elektriske felter .

Dualitet i projektiv geometri

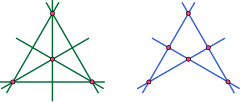
I nogle projicerende plan er det muligt at finde geometriske transformationer, der kortlægger hvert punkt i det projicerende plan til en linje og hver linje i det projicerende plan til et punkt på en incidensbevarende måde. For sådanne planer opstår der et generelt dualitetsprincip i projicerende planer : givet ethvert sætning i et sådant plan projiceret geometri, udveksling af udtrykkene "punkt" og "linje" overalt resulterer i en ny, lige så gyldig sætning. Et simpelt eksempel er, at udsagnet "to punkter bestemmer en unik linje, linjen, der passerer gennem disse punkter" har den dobbelte sætning, at "to linjer bestemmer et unikt punkt, skæringspunktet for disse to linjer". For yderligere eksempler, se Dual sætninger .

En konceptuel forklaring af dette fænomen i nogle planer (især feltplaner) tilbydes af det dobbelte vektorrum. Faktisk svarer punkterne i det projicerende plan til endimensionelle subvektorrum, mens linjerne i det projicerende plan svarer til subvektorrum af dimension 2. Dualiteten i sådanne projektive geometrier stammer fra at tildele et endimensionelt underrummet bestående af de lineære kort, der tilfredsstiller . Som en konsekvens af dimensioneringsformlen for lineær algebra er dette rum todimensionalt, dvs. det svarer til en linje i det projicerende plan, der er knyttet til . ${\ displaystyle \ mathbb {RP} ^ {2}}$${\ displaystyle V \ subset \ mathbb {R} ^ {3}}$${\ displaystyle W}$${\ displaystyle V}$${\ displaystyle (\ mathbb {R} ^ {3}) ^ {*}}$${\ displaystyle f: \ mathbb {R} ^ {3} \ to \ mathbb {R}}$${\ displaystyle f (V) = 0}$${\ displaystyle (\ mathbb {R} ^ {3}) ^ {*}}$

Den (positive bestemte) bilineære form

giver en identifikation af dette projektive plan med . Konkret tildeler dualiteten sin retvinklede . De eksplicitte formler i dualitet i projektiv geometri opstår ved hjælp af denne identifikation. ${\ displaystyle \ mathbb {RP} ^ {2}}$${\ displaystyle V \ subset \ mathbb {R} ^ {3}}$ ${\ displaystyle \ left \ {w \ in \ mathbb {R} ^ {3}, \ langle v, w \ rangle = 0 {\ text {for all}} v \ in V \ right \}}$

Topologiske vektorrum og Hilbert-rum

Inden for topologiske vektorrum findes en lignende konstruktion, der erstatter det dobbelte med det topologiske dobbeltvektorrum . Der er flere forestillinger om topologisk dobbeltrum, og hver af dem giver anledning til et bestemt begreb dualitet. Et topologisk vektorrum, der er kanonisk isomorft til dets bidual , kaldes et

refleksivt rum : ${\ displaystyle X}$${\ displaystyle X ''}$

$${\ displaystyle X \ cong X ''.}$$

Eksempler:

• Som i det endelige dimensionelle tilfælde definerer hvert Hilbert-rum H sit indre produkt ⟨⋅, a et kort
  $${\ displaystyle H \ til H ^ {*}, v \ mapsto (w \ mapsto \ langle w, v \ rangle),}$$

  
  hvilket er en sammenhæng på grund af Riesz-repræsentationssætningen . Som en følge er hvert Hilbert-rum et refleksivt Banach-rum .
• Den dobbelte Normeret plads af en L ^p -space er L ^q , hvor 1 / p + 1 / q = 1 , forudsat at 1 ≤ p <∞ , men den dobbelte af L ^∞ er større end L ¹ . Derfor er L ¹ ikke refleksiv.
• Fordelinger er lineære funktionaliteter på passende funktionsrum. De er et vigtigt teknisk middel i teorien om delvise differentialligninger (PDE): i stedet for at løse en PDE direkte kan det være lettere at først løse PDE i "svag forstand", dvs. finde en distribution, der tilfredsstiller PDE og for det andet at vise, at løsningen faktisk skal være en funktion. Alle faste rum distributioner - , , - er refleksive lokalt konvekse rum. ${\ displaystyle {\ mathcal {D}} '(U)}$${\ displaystyle {\ mathcal {S}} '(\ mathbb {R} ^ {n})}$${\ displaystyle {\ mathcal {C}} ^ {\ infty} (U) '}$

Yderligere dobbelte objekter

Det dobbelte gitter af et gitter L er givet af

$${\ displaystyle \ operatorname {Hom} (L, \ mathbf {Z}),}$$

som bruges til konstruktion af toriske sorter . Den Pontryagin dobbelte af lokalt kompakte topologiske grupper G er givet ved

$${\ displaystyle \ operatorname {Hom} (G, S ^ {1}),}$$

kontinuerlige gruppehomomorfier med værdier i cirklen (med multiplikation af komplekse tal som gruppedrift).

Dobbeltkategorier

Hovedartikel: Dobbelt (kategoriteori)

Modsat kategori og tilstødende funktioner

I en anden gruppe dualiteter oversættes objekterne til en teori til objekter fra en anden teori, og kortene mellem objekter i den første teori oversættes til morfismer i den anden teori, men med omvendt retning. Ved hjælp af sprogkategorien teori , svarer dette til en kontravariant funktor mellem to kategorier C og D :

F : C → D

som for ethvert to objekter X og Y af C giver et kort

Hom _C ( X , Y ) → Hom _D ( F ( Y ), F ( X ))

Denne funktion kan måske ikke være en ækvivalens mellem kategorier . Der er forskellige situationer, hvor et sådant functor er en ækvivalens mellem modsatte kategori C ^op af C , og D . Ved hjælp af en dualitet af denne type kan hver udsagn i den første teori oversættes til en "dobbelt" udsagn i den anden teori, hvor retningen af ​​alle pile skal vendes. Derfor er enhver dualitet mellem kategorierne C og D formelt den samme som en ækvivalens mellem C og D ^op ( C ^op og D ). Imidlertid har de modsatte kategorier under mange omstændigheder ingen iboende betydning, hvilket gør dualitet til et yderligere, separat koncept.

En kategori, der svarer til dens dual, kaldes selv-dual . Et eksempel på selv-dobbelt kategori er kategorien af Hilbert-rum .

Mange kategoriteoretiske forestillinger kommer parvis i den forstand, at de svarer til hinanden, mens de overvejer den modsatte kategori. For eksempel er kartesiske produkter Y ₁ × Y ₂ og usammenhængende fagforeninger Y ₁ ⊔ Y ₂ af sæt dobbelt over for hinanden i den forstand, at

Hom ( X , Y ₁ × Y ₂ ) = Hom ( X , Y ₁ ) × Hom ( X , Y ₂ )

og

Hom ( Y ₁ ⊔ Y ₂ , X ) = Hom ( Y ₁ , X ) × Hom ( Y ₂ , X )

til et sæt X . Dette er et særligt tilfælde af et mere generelt dualitetsfænomen, under hvilket grænser i en kategori C svarer til kolimitter i den modsatte kategori C ^op ; yderligere konkrete eksempler på dette er epimorfier vs. monomorfisme , især faktormoduler (eller grupper osv.) vs. submoduler , direkte produkter vs. direkte summer (også kaldet coproducts for at understrege dualitetsaspektet). Derfor kan bevis for visse udsagn i nogle tilfælde halveres ved hjælp af et sådant dualitetsfænomen. Yderligere begreber Viser relateret ved sådan en kategorisk dualitet er projektive og injektive moduler i homologisk algebra , fibrations og cofibrations i topologi og mere generelt modelkategorier .

To functors F : C → D og G : D → C er adjungerede hvis for alle objekter c i C og d i D

Hom _D (F ( c ), d ) ≅ Hom _C ( c , G ( d )) ,

på en naturlig måde. Faktisk er korrespondancen mellem grænser og kolimitter et eksempel på sammenhænge, ​​da der er et tillæg

colim: C ^I ↔ C : Δ

mellem colimit-funktoren, der tildeler ethvert diagram i C indekseret af en eller anden kategori I, er dens colimit og den diagonale funktor, der kortlægger ethvert objekt c af C til det konstante diagram, der har c overalt. Dually,

Δ: C ↔ C ^I : lim .

Rum og funktioner

Gelfand-dualitet er en dualitet mellem kommutative C * -algebras A og kompakte Hausdorff-mellemrum X er den samme: den tildeler X rummet med kontinuerlige funktioner (som forsvinder ved uendelig) fra X til C , de komplekse tal. Omvendt rummet X kan rekonstrueres fra A som spektret af A . Både Gelfand- og Pontryagin-dualitet kan udledes på en stort set formel, kategoritetoretisk måde.

I samme ånd er der en dobbelthed i algebraisk geometri mellem kommutativ ring og affine ordninger : til hver kommutativ ring A er en affin spektrum, Spec A . Omvendt givet en affin ordning S , får man tilbage en ring ved at tage globale afsnit af strukturen neg O _S . Desuden er ringhomomorfier i en-til-en-korrespondance med morfismer af affine-ordninger, hvorved der er en ækvivalens

(Kommutative ringe) ^op ≅ (affine-ordninger)

Affine-ordninger er de lokale byggesten i ordningerne . Det tidligere resultat fortæller derfor, at den lokale teori om skemaer er den samme som kommutativ algebra , studiet af kommutative ringe.

Ikke-kommutativ geometri henter inspiration fra Gelfand-dualitet og studerer ikke-kommutative C * -algebras, som om de var funktioner på et forestillet rum. Tannaka – Kerin-dualitet er en ikke-kommutativ analog af Pontryagin-dualitet.

Galois forbindelser

I en række situationer stammer de to kategorier, der er dobbelte i forhold til hinanden, faktisk fra delvist ordnede sæt, dvs. der er en forestilling om, at et objekt "er mindre" end et andet. En dualitet, der respekterer de pågældende ordrer, er kendt som en Galois-forbindelse . Et eksempel er den standard dualitet i Galois-teorien, der er nævnt i indledningen: en større feltudvidelse svarer - under kortlægningen, der tildeler enhver udvidelse L inside K (inde i et fast større felt Ω) Galois-gruppen Gal (Ω / L ) - en mindre gruppe.

Samlingen af ​​alle åbne delmængder af et topologisk rum X danner en komplet Heyting-algebra . Der er en dualitet, kendt som Stone-dualitet , der forbinder ædru rum og rumlige lokaliteter .

• Birkhoffs repræsentationssætning vedrørende distribuerende gitter og delordrer

Pontryagin dualitet

Pontryagin-dualitet giver en dualitet i kategorien af lokalt kompakte abeliske grupper : givet en sådan gruppe G , karaktergruppen

χ ( G ) = Hom ( G , S ¹ )

afgivet kontinuerlige gruppehomomorfi fra G til cirkel gruppe S ¹ kan være udstyret med den kompakte-åbne topologi . Pontryagin-dualitet siger, at karaktergruppen igen er lokalt kompakt abelsk og det

G ≅ χ (χ ( G )).

Desuden svarer diskrete grupper til kompakte abeliske grupper ; endelige grupper svarer til begrænsede grupper. På den ene side er Pontryagin et specielt tilfælde af Gelfand-dualitet. På den anden side er det den konceptuelle årsag til Fourier-analyse , se nedenfor.

Analytiske dualiteter

I analysen løses problemer ofte ved at gå til den dobbelte beskrivelse af funktioner og operatører.

Fourier-transform skifter mellem funktioner i et vektorrum og dets dobbelte:

$${\ displaystyle {\ widehat {f}} (\ xi): = \ int _ {- \ infty} ^ {\ infty} f (x) \ e ^ {- 2 \ pi ix \ xi} \, dx,}$$

og omvendt

$${\ displaystyle f (x) = \ int _ {- \ infty} ^ {\ infty} {\ widehat {f}} (\ xi) \ e ^ {2 \ pi ix \ xi} \, d \ xi.}$$

Hvis f er en L ² -funktionen på R eller R ^N , siger, derefter så er og . Desuden udskifter transformationen multiplikations- og konvolutionsoperationer på de tilsvarende funktionsrum . En begrebsmæssig redegørelse for Fourier transformation opnås ved den førnævnte Pontryagin dobbelthed, påføres lokalt kompakte grupper R (eller R ^N etc.): enhver karakter R er givet ved ξ ↦ e ^{-2 πixξ} . Den dualiserende karakter af Fourier-transformation har mange andre manifestationer, for eksempel i alternative beskrivelser af kvantemekaniske systemer med hensyn til koordinat- og momentrepræsentationer. ${\ displaystyle {\ widehat {f}}}$${\ displaystyle f (-x) = {\ widehat {\ widehat {f}}} (x)}$

• Laplace-transformation svarer til Fourier-transformation og udveksler operatorer af multiplikation med polynomer med konstant koefficient lineære differentielle operatorer .
• Legendre transformation er en vigtig analytisk dualitet, der skifter mellem hastigheder i Lagrangian-mekanik og momenta i Hamilton-mekanik .

Homologi og kohomologi

Teoremer, der viser, at bestemte objekter af interesse er de dobbelte rum (i betydningen lineær algebra) for andre objekter af interesse kaldes ofte dualiteter . Mange af disse dualiteter er givet ved en bilinær parring af to K- vektorrum

A ⊗ B → K .

Til perfekte parringer , er der derfor en isomorfi af A til den dobbelte af B .

Poincaré-dualitet

Poincaré-dualitet af et glat kompakt kompleks manifold X er givet ved en parring af ental kohomologi med C- koefficienter (ækvivalent, skovkohomologi af den konstante skive C )

H ⁱ (X) ⊗ H ^{2 n - i} (X) → C ,

hvor n er (kompleks) dimension X . Poincaré-dualitet kan også udtrykkes som et forhold mellem ental homologi og de Rham kohomologi ved at hævde, at kortet

${\ displaystyle (\ gamma, \ omega) \ mapsto \ int _ {\ gamma} \ omega}$

(integrering af en differentiel k-form over en 2 n - k - (ægte) -dimensionel cyklus) er en perfekt parring.

Poincaré-dualitet vender også dimensioner; det svarer til det faktum, at hvis en topologisk manifold er repræsenteret som et cellekompleks , så repræsenterer det dobbelte af komplekset (en højere-dimensionel generalisering af den plane graf dobbelt) det samme manifold. I Poincaré-dualitet reflekteres denne homomorfisme i en isomorfisme fra den k th homologigruppe og ( n  -  k ) th cohomology group.

Dualitet i algebraisk og aritmetisk geometri

Den samme dobbelthed mønster gælder for en glat projektiv række over et adskilleligt lukket område , under anvendelse af l-adic cohomology med Q _ℓ -coefficients stedet. Dette er yderligere generaliseret til muligvis entalsvarianter ved hjælp af krydsnings kohomologi i stedet for en dualitet kaldet Verdier dualitet . Serredualitet eller sammenhængende dualitet svarer til udsagnene ovenfor, men gælder i stedet for kohomologi af sammenhængende skiver .

Med stigende niveau af generalitet viser det sig, at en stigende mængde teknisk baggrund er nyttigt eller nødvendigt for at forstå disse sætninger: Den moderne formulering af disse dualiteter kan udføres ved hjælp af afledte kategorier og visse direkte og inverse billedfunktioner af skiver (med hensyn til den klassiske analytiske topologi på manifolder til Poincaré-dualitet, l-adiske skiver og den étale topologi i det andet tilfælde og med hensyn til sammenhængende skiver til sammenhængende dualitet).

Endnu en anden gruppe af lignende dobbelthed udsagn er stødt på i arithmetics : Etale cohomology af finite , lokale og globale felter (også kendt som Galois kohomologi , eftersom Etale cohomology over en mark svarer til gruppe cohomology af (absolut) Galois gruppe af marken) indrømme lignende parringer. Den absolutte Galois gruppe G ( F _q ) af et finit felt, for eksempel, er isomorf til , den

profinite færdiggørelse af Z , heltal. Derfor er den perfekte parring (til enhver G- modul M ) ${\ displaystyle {\ widehat {\ mathbf {Z}}}}$

H ⁿ ( G , M ) × H ^{1− n} ( G , Hom ( M , Q / Z )) → Q / Z

er en direkte konsekvens af Pontryagin-dualitet af begrænsede grupper. For lokale og globale felter findes lignende udsagn ( lokal dualitet og global eller Poitou – Tate-dualitet ).

Se også

• Adjoint functor
• Autonom kategori
• Dobbelt abelsk variation
• Dobbelt basis
• Dobbelt (kategoriteori)
• Dobbelt kode
• Dualitet (elektroteknik)
• Dualitet (optimering)
• Dualiseringsmodul
• Dualisering af skive
• Dobbelt gitter
• Dobbelt norm
• Dobbelt tal , en bestemt associerende algebra ; udtrykket "dobbelt" her er synonymt med dobbelt og er ikke relateret til forestillingerne ovenfor.
• Koszul-dualitet
• Langlands dobbelt
• Lineær programmering # Dualitet
• Liste over dualiteter
• Matlis dualitet
• Petrie dualitet
• Pontryagin dualitet
• S-dualitet
• T-dualitet , spejlsymmetri

Bemærkninger

Referencer

Dualitet generelt

• Atiyah, Michael (2007), Dualitet i matematik og fysik , forelæsningsnotater fra Institut de Matematica de la Universitat de Barcelona (IMUB).
• Kostrikin, AI (2001) [1994], "Duality" , Encyclopedia of Mathematics , EMS Press CS1 maint: modløs parameter ( link ) .
• Gowers, Timothy (2008), "III.19 Duality", Princeton Companion to Mathematics , Princeton University Press, s. 187-190 .
• Cartier, Pierre (2001), "En gal dags arbejde: fra Grothendieck til Connes og Kontsevich. Udviklingen af ​​begreberne rum og symmetri" , Bulletin of the American Mathematical Society , New Series, 38 (4): 389–408, doi : 10.1090 / S0273-0979-01-00913-2 , ISSN   0002-9904 , MR   1848254 (en ikke-teknisk oversigt over flere aspekter af geometri, herunder dualiteter)

Dualitet i algebraisk topologi

• James C. Becker og Daniel Henry Gottlieb, A History of Duality in Algebraic Topology

Specifikke dualiteter

• Artstein-Avidan, Shiri ; Milman, Vitali (2008), "Begrebet dualitet for målefremskrivninger af konvekse kroppe", Journal of Functional Analysis , 254 (10): 2648–66, doi : 10.1016 / j.jfa.2007.11.008 . Også forfatterens side .
• Artstein-Avidan, Shiri; Milman, Vitali (2007), "En karakterisering af begrebet dualitet" , Elektroniske forskningsmeddelelser i matematiske videnskaber , 14 : 42-59, arkiveret fra originalen den 2011-07-24 , hentet 2009-05-30 . Også forfatterens side .
• Dwyer, William G .; Spaliński, Jan (1995), "Homotopiteorier og modelkategorier" , Håndbog for algebraisk topologi , Amsterdam: Nordholland, s. 73–126, MR   1361887
• Fulton, William (1993), Introduktion til toriske sorter , Princeton University Press , ISBN   978-0-691-00049-7
• Griffiths, Phillip ; Harris, Joseph , principper for algebraisk geometri , Wiley Classics Library, New York: John Wiley & Sons , ISBN   978-0-471-05059-9 , MR   1288523
• Hartshorne, Robin (1966), Residues and Duality , Lecture Notes in Mathematics, 20 , Springer-Verlag , s. 20–48, ISBN   978-3-540-34794-1
• Hartshorne, Robin (1977), Algebraic Geometry , Springer-Verlag , ISBN   978-0-387-90244-9 , MR   0463157 , OCLC   13348052
• Iversen, Birger (1986), Cohomology of sheaves , Universitext, Springer-Verlag , ISBN   978-3-540-16389-3 , MR   0842190
• Joyal, André ; Street, Ross (1991), "En introduktion til Tannaka-dualitet og kvantegrupper" (PDF) , Kategoriteori , Forelæsningsnotater i matematik, 1488 , Springer-Verlag , s. 413–492, doi : 10.1007 / BFb0084235 , ISBN   978-3-540-46435-8 , MR   1173027
• Lam, Tsit-Yuen (1999), Forelæsninger om moduler og ringe , Graduate Texts in Mathematics, 189 , Springer-Verlag , ISBN   978-0-387-98428-5 , MR   1653294
• Lang, Serge (2002), Algebra , Graduate Texts in Mathematics, 211 , Springer-Verlag , ISBN   978-0-387-95385-4 , MR   1878556
• Loomis, Lynn H. (1953), En introduktion til abstrakt harmonisk analyse , D. Van Nostrand, s. X + 190, hdl : 2027 / uc1.b4250788
• Mac Lane, Saunders (1998), Kategorier for den Arbejdende Matematiker (2. udgave), Springer-Verlag , ISBN   978-0-387-98403-2
• Mazur, Barry (1973), "Notes on étale cohomology of number fields", Annales Scientifiques de l'École Normale Supérieure , Série 4, 6 (4): 521–552, doi : 10.24033 / asens.1257 , ISSN   0012-9593 , MR   0344254
• Milne, James S. (1980), Étale cohomology , Princeton University Press , ISBN   978-0-691-08238-7
• Milne, James S. (2006), aritmetiske dualitetssætninger (2. udgave), Charleston, South Carolina: BookSurge, LLC, ISBN   978-1-4196-4274-6 , MR   2261462
• Negrepontis, Joan W. (1971), "Dualitet i analyse set fra tredobler", Journal of Algebra , 19 (2): 228-253, doi : 10.1016 / 0021-8693 (71) 90105-0 , ISSN   0021-8693 , MR   0280571
• Veblen, Oswald ; Young, John Wesley (1965), Projektiv geometri. Vol. 1, 2 , Blaisdell Publishing Co. Ginn and Co., MR   0179666
• Weibel, Charles A. (1994), En introduktion til homologisk algebra , Cambridge University Press , ISBN   978-0-521-55987-4 , MR   1269324
• Edwards, RE (1965). Funktionel analyse. Teori og anvendelser . New York: Holt, Rinehart og Winston. ISBN   0030505356 .