Keglesnit - Conic section

I matematik er et keglesnit (eller simpelthen kegle ) en kurve opnået som skæringspunktet mellem en kegles overflade og et plan . De tre typer af keglesnit er hyperbola , parabel og ellipse ; den cirkel er et særligt tilfælde af ellipsen, men historisk set blev det undertiden kaldes en fjerde type. De gamle græske matematikere studerede keglesnit og kulminerede omkring 200 f.Kr. med Apollonius af Pergas systematiske arbejde med deres egenskaber.

De keglesnit i det euklidiske plan har forskellige kendetegn, hvoraf mange kan bruges som alternative definitioner. En sådan egenskab definerer en ikke-cirkulær kegle til at være sættet af de punkter, hvis afstande til et bestemt punkt, kaldet et fokus , og en bestemt linje, kaldet en directrix , er i et fast forhold, kaldet excentriciteten . Typen af ​​kegle bestemmes af værdien af ​​excentriciteten. I analytisk geometri kan en kegle defineres som en plan algebraisk kurve af grad 2; det vil sige som sæt af punkter, hvis koordinater opfylder en kvadratisk ligning i to variabler, som kan skrives i matrixform . Denne ligning gør det muligt at udlede og udtrykke algebraisk de geometriske egenskaber af keglesnit.

I det euklidiske plan fremstår de tre typer af keglesnit ganske forskellige, men deler mange egenskaber. Ved at forlænge det euklidiske plan til at omfatte en linje i det uendelige og opnå et projektivt plan , forsvinder den tilsyneladende forskel: grenene af en hyperbol mødes i to punkter ved uendeligt, hvilket gør det til en enkelt lukket kurve; og de to ender af en parabel mødes for at gøre det til en lukket kurve, der tangerer linjen i det uendelige. Yderligere forlængelse, ved at udvide de reelle koordinater til at indrømme komplekse koordinater, giver midler til at se denne forening algebraisk.

Euklidisk geometri

De keglesnit er blevet undersøgt i tusinder af år og har givet en rig kilde til interessante og smukke resultater i euklidisk geometri .

Definition

En konisk er den opnåede kurve som skæringen af en plan , kaldet skæreplanet , med overfladen af en dobbelt kegle (en kegle med to nappes ). Det antages normalt, at keglen er en rigtig cirkulær kegle med henblik på let beskrivelse, men dette er ikke påkrævet; enhver dobbeltkegle med et cirkulært tværsnit er tilstrækkeligt. Planer, der passerer gennem keglens toppunkt, skærer keglen i et punkt, en linje eller et par krydsende linjer. Disse kaldes degenererede kegler, og nogle forfattere betragter dem slet ikke som kegler. Medmindre andet er angivet, vil "kegle" i denne artikel referere til en ikke-degenereret kegle.

Der er tre typer af kegler: ellipse , parabel og hyperbola . Den cirkel er en speciel form for ellipse, selvom historisk Apollonius betragtes som en fjerde type. Ellipser opstår, når skæringspunktet mellem keglen og planet er en lukket kurve . Cirklen opnås, når skæreplanet er parallelt med planet for keglens genererende cirkel; for en højre kegle betyder det, at skæreplanet er vinkelret på aksen. Hvis skæreplanet er parallelt med nøjagtigt en genereringslinie i keglen, er keglen ubegrænset og kaldes en parabel . I det resterende tilfælde er figuren en hyperbola : flyet skærer begge halvdele af keglen og producerer to separate ubegrænsede kurver.

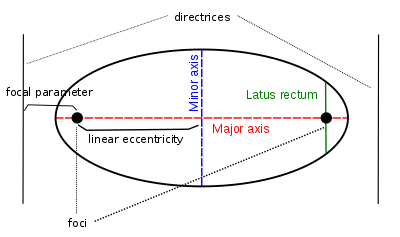
Eksentricitet, fokus og directrix

Alternativt kan man definere et keglesnit udelukkende med hensyn til plangeometri: det er stedet for alle punkter P, hvis afstand til et fast punkt F (kaldet fokus ) er et konstant multiplum (kaldet excentricitet e ) af afstanden fra P til en fast linje L (kaldet directrix ). For 0 < e <1 får vi en ellipse, for e = 1 en parabel og for e > 1 en hyperbola.

En cirkel er et begrænsende tilfælde og er ikke defineret af en fokus og directrix i det euklidiske plan. Excentriciteten af ​​en cirkel er defineret til at være nul, og dens fokus er midten af ​​cirklen, men dens directrix kan kun tages som linjen i det uendelige i det projektive plan.

En ellipses excentricitet kan ses som et mål for, hvor langt ellipsen afviger fra at være cirkulær.

Hvis vinklen mellem keglens overflade og dens akse er og vinklen mellem skæreplanet og aksen er excentriciteten${\ displaystyle \ beta}$${\ displaystyle \ alpha,}$${\ displaystyle {\ frac {\ cos \ alpha} {\ cos \ beta}}.}$

Et bevis på, at de ovennævnte kurver, der er defineret af fokus-directrix-egenskaben, er de samme som dem, der opnås af fly, der skærer en kegle, letter ved brug af Dandelin-kugler .

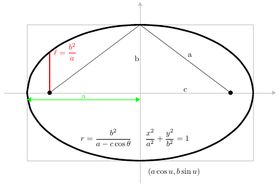
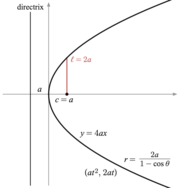
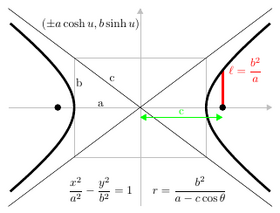
Alternativt kan en ellipse defineres i form af to fokuspunkter, som locus af punkter, for hvilke summen af ​​afstandene til de to foci er 2 a ; mens en hyperbola er det sted, for hvilket afstanden er 2 a . (Her er a den halvstore akse defineret nedenfor.) En parabel kan også defineres med hensyn til dens fokus og latus rectum line (parallelt med directrix og passerer gennem fokus): det er locus af punkter, hvis afstand til fokus plus eller minus afstanden til linjen er lig med 2 a ; plus, hvis punktet er mellem directrix og latus rectum, minus ellers.

Kegleparametre

Ud over excentriciteten ( e ), foci og directrix er forskellige geometriske træk og længder forbundet med et keglesnit.

Den hovedakse er linjen mellem brændpunkter af en ellipse eller hyperbel, og dens midtpunkt er kurvens centrum . En parabel har ikke noget center.

Den lineære excentricitet ( c ) er afstanden mellem centrum og et fokus.

Den latus endetarmen er den akkord parallelt med ledelinje og passerer gennem et fokus; dens halve længde er semi-latus rectum ( ℓ ).

Den fokale parameter ( p ) er afstanden fra fokus til den tilsvarende ledelinjen.

Den hovedakse er korden mellem de to toppunkter: den længste korde af en ellipse, den korteste korde mellem grenene på en hyperbel. Dens halvlængde er den halvstore akse ( a ). Når en ellipse eller hyperbel er i standard position som i ligningerne nedenfor, med foci på x -aksen og center på oprindelse, knudepunkter af den koniske har koordinaterne (- a , 0) og ( a , 0) , med en ikke-negativ.

Den mindre akse er den korteste diameter af en ellipse, og dens halve længde er den halve lilleakse ( b ), den samme værdi b som i standard ligningen nedenfor. Til analogi kaldes parameter b i standardligningen for en hyperbol også semi-minor-aksen.

Følgende relationer holder:

• ${\ displaystyle \ \ ell = pe}$
• ${\ displaystyle \ c = ae}$
• ${\ displaystyle \ p+c = {\ frac {a} {e}}}$

For keglesnit i standard position, disse parametre har følgende værdier, idet . ${\ displaystyle a, b> 0}$

keglesnit	ligning	excentricitet ( e )	lineær excentricitet ( c )	semi-latus rectum ( ℓ )	fokal parameter ( p )
cirkel	${\ displaystyle x^{2}+y^{2} = a^{2} \,}$	${\ displaystyle 0 \,}$	${\ displaystyle 0 \,}$	${\ displaystyle a \,}$	${\ displaystyle \ infty}$
ellipse	${\ displaystyle {\ frac {x^{2}} {a^{2}}}+{\ frac {y^{2}} {b^{2}}} = 1}$	${\ displaystyle {\ sqrt {1-{\ frac {b^{2}} {a^{2}}}}}}}$	${\ displaystyle {\ sqrt {a^{2} -b^{2}}}}$	${\ displaystyle {\ frac {b^{2}} {a}}}$	${\ displaystyle {\ frac {b^{2}} {\ sqrt {a^{2} -b^{2}}}}}}$
parabel	${\ displaystyle y^{2} = 4ax \,}$	${\ displaystyle 1 \,}$	Ikke relevant	${\ displaystyle 2a \,}$	${\ displaystyle 2a \,}$
hyperbola	${\ displaystyle {\ frac {x^{2}} {a^{2}}}-{\ frac {y^{2}} {b^{2}}} = 1}$	${\ displaystyle {\ sqrt {1+{\ frac {b^{2}} {a^{2}}}}}}$	${\ displaystyle {\ sqrt {a^{2}+b^{2}}}}$	${\ displaystyle {\ frac {b^{2}} {a}}}$	${\ displaystyle {\ frac {b^{2}} {\ sqrt {a^{2}+b^{2}}}}}$

Standardformularer i kartesiske koordinater

Efter indførelse af kartesiske koordinater kan egenskaben focus-directrix bruges til at producere ligningerne opfyldt af punkterne i det keglesnit. Ved hjælp af en ændring af koordinater ( rotation og translation af akser ) kan disse ligninger sættes i standardformer . For ellipser og hyperboler har en standardform x -aksen som hovedakse og oprindelsen (0,0) som centrum. Hjørnerne er (± a , 0) og foci (± c , 0) . Definer b ved ligningerne c ² = a ² - b ² for en ellipse og c ² = a ² + b ² for en hyperbola. For en cirkel, c = 0 så a ² = b ² . For parablen, standard form har fokus på x -aksen ved punktet ( a , 0) og ledelinjen linien med ligningen x = - a . I standardform passerer parablen altid gennem oprindelsen.

For en rektangulær eller ligesidet hyperbola , en hvis asymptoter er vinkelret, er der en alternativ standardform, hvor asymptoterne er koordinatakser og linjen x = y er hovedaksen. Fokuserne har derefter koordinater ( c , c ) og ( - c , - c ) .

• Cirkel: x ² + y ² = a ²
• Ellipse: x ²/a ² + y ²/b ² = 1
• Parabel: y ² = 4 økse med en > 0
• Hyperbola: x ²/a ² - y ²/b ² = 1
• Rektangulær hyperbola: xy =c ²/2

De fire første af disse former er symmetriske om både x -aksen og y -aksen (for cirklen, ellipse og hyperbola) eller kun om x -aksen (for parabolen). Den rektangulære hyperbol er imidlertid i stedet symmetrisk omkring linjerne y = x og y = - x .

Disse standardformularer kan skrives parametrisk som,

• Cirkel : ( en cos θ , en synd θ ) ,
• Ellipse : ( a cos θ , b sin θ ) ,
• Parabel : ( ved ² , 2 ved ) ,
• Hyperbola : ( a sec θ , b tan θ ) eller (± a cosh u , b sinh u ) ,
• Rektangulær hyperbola : hvor${\ displaystyle (d \, t, {\ frac {d} {t}})}$${\ displaystyle d = {\ frac {c} {\ sqrt {2}}}.}$

Generel kartesisk form

I det kartesiske koordinatsystem er grafen for en kvadratisk ligning i to variabler altid et keglesnit (selvom det kan være degenereret ), og alle keglesnit opstår på denne måde. Den mest generelle ligning er af formen

${\ displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F = 0,}$

med alle koefficienter reelle tal og A, B, C ikke alle nul.

Matrix notation

Ovenstående ligning kan skrives i matrixnotation som

${\ displaystyle \ left ({\ begin {matrix} x & y \ end {matrix}} \ right) \ left ({\ begin {matrix} A & B/2 \\ B/2 & C \ end {matrix}} \ right) \ left ({\ begin {matrix} x \\ y \ end {matrix}} \ højre)+\ venstre ({\ begin {matrix} D&E \ end {matrix}} \ højre) \ venstre ({\ begin {matrix} x \\ y \ end {matrix}} \ højre)+F = 0.}$

Den generelle ligning kan også skrives som

${\ displaystyle \ left ({\ begin {matrix} x & y & 1 \ end {matrix}} \ right) \ left ({\ begin {matrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \ end {matrix}} \ right) \ left ({\ begin {matrix} x \\ y \\ 1 \ end {matrix}} \ right) = 0.}$

Denne form er en specialisering af den homogene form, der bruges i de mere generelle rammer for projektiv geometri (se nedenfor ).

Diskriminerende

De keglesnit, der er beskrevet i denne ligning, kan klassificeres i form af værdien , kaldet ligningens diskriminant . Således er diskriminanten - 4Δ, hvor Δ er matrix -determinanten${\ displaystyle B^{2} -4AC}$ ${\ displaystyle \ left | {\ begin {matrix} A & B/2 \\ B/2 & C \ end {matrix}} \ højre |.}$

Hvis keglen er ikke-degenereret , så:

• hvis B ² - 4 AC <0 , repræsenterer ligningen en ellipse ;
  • hvis A = C og B = 0 , repræsenterer ligningen en cirkel , som er et specielt tilfælde af en ellipse;
• hvis B ² - 4 AC = 0 , repræsenterer ligningen en parabel ;
• hvis B ² - 4 AC > 0 , repræsenterer ligningen en hyperbola ;
  • hvis A + C = 0 , repræsenterer ligningen en rektangulær hyperbola .

Med notationen her, A og B er polynomiumskoefficienter i modsætning til nogle kilder, der angiver de Banens store og semiminor akser som A og B .

Invarianter

Den diskriminerende B ² - 4 AC i den koniske sektions kvadratiske ligning (eller ækvivalent determinanten AC - B ² /4 i 2 × 2 matrixen) og mængden A + C ( sporet af 2 × 2 matrix) er invariante under vilkårlige rotationer og oversættelser af koordinatakserne, som er determinanten for 3 × 3 -matrixen ovenfor . Konstantleddet F og summen D ² + E ² er invariant under kun rotation.

Eksentricitet med hensyn til koefficienter

Når den keglesnit er skrevet algebraisk som

${\ displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F = 0, \,}$

excentriciteten kan skrives som en funktion af koefficienterne i den kvadratiske ligning. Hvis 4 AC = B ² er keglen en parabel og dens excentricitet er lig med 1 (forudsat at den ikke er degenereret). Ellers forudsat at ligningen repræsenterer enten en ikke-degenereret hyperbola eller ellipse, er excentriciteten givet ved

${\ displaystyle e = {\ sqrt {\ frac {2 {\ sqrt {(AC)^{2}+B^{2}}}} {\ eta (A+C)+{\ sqrt {(AC)^ {2}+B^{2}}}}}}}$

hvor η = 1 hvis determinanten af 3 × 3 -matrixen ovenfor er negativ og η = −1 hvis denne determinant er positiv.

Det kan også vises, at excentriciteten er en positiv løsning af ligningen

${\ displaystyle \ Delta e^{4}+[(A+C)^{2} -4 \ Delta] e^{2}-[(A+C)^{2} -4 \ Delta] = 0, }$

hvor igen Denne har netop en positiv løsning - excentriciteten - i tilfælde af en parabel eller ellipse, mens den i tilfælde af en hyperbola har to positive løsninger, hvoraf den ene er excentriciteten. ${\ displaystyle \ Delta = AC-{\ frac {B^{2}} {4}}.}$

Konvertering til kanonisk form

I tilfælde af en ellipse eller hyperbola, ligningen

${\ displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F = 0 \,}$

kan konverteres til kanonisk form i transformerede variabler som ${\ displaystyle {\ tilde {x}}, {\ tilde {y}}}$

${\ displaystyle {\ frac {{\ tilde {x}}^{2}} {-S/(\ lambda _ {1}^{2} \ lambda _ {2})}}+{\ frac {{\ tilde {y}}^{2}} {-S/(\ lambda _ {1} \ lambda _ {2}^{2})}} = 1,}$

eller tilsvarende

${\ displaystyle {\ frac {{\ tilde {x}}^{2}} {-S/(\ lambda _ {1} \ Delta)}}+{\ frac {{\ tilde {y}}^{2 }} {-S/(\ lambda _ {2} \ Delta)}} = 1,}$

hvor og er matrixens egenværdier - det vil sige løsningerne i ligningen ${\ displaystyle \ lambda _ {1}}$${\ displaystyle \ lambda _ {2}}$${\ displaystyle \ left ({\ begin {matrix} A & B/2 \\ B/2 & C \ end {matrix}} \ right)}$

${\ displaystyle \ lambda ^{2}-(A +C) \ lambda +(AC- (B/2) ^{2}) = 0}$

- og er determinant for 3 × 3 matrix ovenfor , og er igen determinant for 2 × 2 matrix. I tilfælde af en ellipse angives firkanterne for de to halvakser af nævnerne i kanonisk form. ${\ displaystyle S}$${\ displaystyle \ Delta = \ lambda _ {1} \ lambda _ {2}}$

Polære koordinater

I polære koordinater er et keglesnit med ét fokus på oprindelsen og eventuelt det andet med en negativ værdi (for en ellipse) eller en positiv værdi (for en hyperbola) på x -aksen givet ved ligningen

${\ displaystyle r = {\ frac {l} {1+e \ cos \ theta}},}$

hvor e er excentriciteten og l er semi-latus rectum.

Som ovenfor er grafen for e = 0 en cirkel, for 0 < e <1 er grafen en ellipse, for e = 1 en parabel og for e > 1 en hyperbola.

Den polære form af ligningen af ​​en kegle bruges ofte i dynamik ; for eksempel at bestemme kredsløb for objekter, der kredser om Solen.

Ejendomme

Ligesom to (forskellige) punkter bestemmer en linje, bestemmer fem punkter en kegle . Formelt set, givet alle fem punkter i planet i generel lineær position , hvilket betyder ingen tre kollinære , er der en unik kegle, der passerer gennem dem, som vil være ikke-degenereret; dette er sandt i både det euklidiske plan og dets forlængelse, det virkelige projektive plan. I betragtning af alle fem punkter går der en kegle igennem dem, men hvis tre af punkterne er kollinære, bliver keglen degenereret (reducerbar, fordi den indeholder en linje), og er muligvis ikke unik; se yderligere diskussion .

Fire punkter i planet i generel lineær position bestemmer en unik kegle, der passerer gennem de tre første punkter og har det fjerde punkt som centrum. At kende midten svarer således til at kende to punkter på keglen med det formål at bestemme kurven.

Desuden bestemmes en kegle af enhver kombination af k -punkter i den generelle position, den passerer igennem og 5 - k linjer, der er tangent til den, for 0≤ k ≤5.

Ethvert punkt i planet er på enten nul, en eller to tangentlinjer i en kegle. Et punkt på kun en tangentlinje er på keglen. Et punkt på ingen tangentlinie siges at være et indre punkt (eller indre punkt ) i keglen, mens et punkt på to tangentlinjer er et ydre punkt (eller ydre punkt ).

Alle de keglesnit deler en refleksionsegenskab, der kan angives som: Alle spejle i form af et ikke-degenereret keglesnit reflekterer lys, der kommer fra eller går mod det ene fokus mod eller væk fra det andet fokus. I tilfælde af parabolen skal det andet fokus betragtes som uendeligt langt væk, så lysstrålerne, der går mod eller kommer fra det andet fokus, er parallelle.

Pascals sætning vedrører collineariteten af ​​tre punkter, der er konstrueret ud fra et sæt på seks punkter på enhver ikke-degenereret kegle. Sætningen gælder også for degenererede kegler bestående af to linjer, men i så fald er den kendt som Pappus sætning .

Ikke-degenererede keglesnit er altid " glatte ". Dette er vigtigt for mange applikationer, såsom aerodynamik, hvor en glat overflade er påkrævet for at sikre laminær strømning og for at forhindre turbulens .

Historie

Menaechmus og tidlige værker

Det menes, at den første definition af en keglesnit blev givet af Menaechmus (død 320 fvt) som en del af hans løsning på Delian -problemet ( Duplikering af terningen ). Hans arbejde overlevede ikke, ikke engang de navne, han brugte til disse kurver, og er kun kendt gennem sekundære konti. Den definition, der blev brugt på det tidspunkt, adskiller sig fra den, der almindeligvis bruges i dag. Kegler blev konstrueret ved at dreje en højre trekant omkring et af dens ben, så hypotenusen genererer overfladen af ​​keglen (en sådan linje kaldes en generatrix ). Tre typer kegler blev bestemt af deres toppunktvinkler (målt med dobbelt så stor vinkel, som hypotenusen dannede, og benet drejes rundt i den højre trekant). Det keglesnit blev derefter bestemt ved at krydse en af ​​disse kegler med et plan trukket vinkelret på en generatrix. Keglens type bestemmes af typen af ​​kegle, det vil sige af den vinkel, der dannes ved keglens toppunkt: Hvis vinklen er spids, er keglen en ellipse; hvis vinklen er rigtig, så er keglen en parabel; og hvis vinklen er stump, så er keglen en hyperbola (men kun en gren af ​​kurven).

Euclid (fl. 300 fvt) siges at have skrevet fire bøger om kegler, men disse gik også tabt. Archimedes (død c.  212 fvt) vides at have studeret kegler, efter at have bestemt området afgrænset af en parabel og en akkord i Quadrature of the Parabola . Hans største interesse var med hensyn til måling af områder og mængder af figurer relateret til keglerne og en del af dette værk overlever i hans bog om faststofferne i revolutionen af ​​kegler, om koboider og kugler .

Apollonius af Perga

De største fremskridt i studiet af kegler fra de gamle grækere skyldes Apollonius af Perga (død ca.  190 fvt), hvis koniske sektioner eller kegler i otte bind opsummerede og i vid udstrækning udvidede eksisterende viden. Apollonius 'undersøgelse af egenskaberne ved disse kurver gjorde det muligt at vise, at ethvert plan, der skærer en fast dobbeltkegle (to napped), uanset dens vinkel, vil producere en kegle i henhold til den tidligere definition, hvilket fører til den definition, der almindeligvis bruges i dag. Cirkler, der ikke er konstruerbare ved den tidligere metode, kan også opnås på denne måde. Dette kan forklare, hvorfor Apollonius betragtede cirkler som en fjerde type keglesnit, en sondring, der ikke længere foretages. Apollonius brugte navnene 'ellipse', 'parabel' og 'hyperbola' til disse kurver og lånte terminologien fra tidligere Pythagoras arbejde på områder.

Pappus fra Alexandria (død ca.  350 e.Kr.) krediteres for at have forklaret betydningen af ​​begrebet konisk fokus og detaljeret det relaterede koncept om en directrix , herunder tilfældet med parabolen (som mangler i Apollonius kendte værker).

Al-Kuhi

Et instrument til at tegne keglesnit blev først beskrevet i 1000 CE af den islamiske matematiker Al-Kuhi .

Omar Khayyám

Apollonius 'arbejde blev oversat til arabisk, og meget af hans arbejde overlever kun gennem den arabiske version. Perserne fandt anvendelser af teorien, især den persiske matematiker og digter Omar Khayyám , der fandt en geometrisk metode til at løse kubiske ligninger ved hjælp af keglesnit.

Europa

Johannes Kepler udvidede teorien om kegle gennem " kontinuitetsprincippet ", en forløber for begrebet grænser. Kepler brugte først udtrykket 'foci' i 1604.

Girard Desargues og Blaise Pascal udviklede en teori om kegler ved hjælp af en tidlig form for projektiv geometri, og dette var med til at give drivkraft til studiet af dette nye felt. Især opdagede Pascal en sætning kendt som hexagrammum mysticum, hvorfra mange andre egenskaber ved kegler kan udledes.

René Descartes og Pierre Fermat anvendte begge deres nyopdagede analytiske geometri til studiet af kegler. Dette havde den virkning at reducere de geometriske problemer med kegler til problemer i algebra. Imidlertid var det John Wallis i sin afhandling Tractatus de sectionibus conicis fra 1655, der først definerede de keglesnit som forekomster af ligninger af anden grad. Jan de Witt 's Elementa Curvarum Linearum blev skrevet tidligere, men blev offentliggjort senere, og starter med Keplers kinematiske konstruktion af keglerne og udvikler derefter de algebraiske ligninger. Dette værk, der anvender Fermats metode og Descartes 'notation, er blevet beskrevet som den første lærebog om emnet. De Witt opfandt udtrykket 'directrix'.

Ansøgninger

Keglesnit er vigtige i astronomi : banerne mellem to massive objekter, der interagerer i henhold til Newtons lov om universel tyngdekraft, er keglesnit, hvis deres fælles massecenter anses for at være i ro. Hvis de er bundet sammen, vil de begge spore ellipser; hvis de bevæger sig fra hinanden, vil de begge følge paraboler eller hyperboler. Se to-kropsproblem .

De keglesektioners reflekterende egenskaber bruges til design af søgelys, radioteleskoper og nogle optiske teleskoper. Et søgelys bruger et parabolsk spejl som reflektor, med en pære i fokus; og en lignende konstruktion bruges til en parabolsk mikrofon . Det 4,2 meter høje Herschel optiske teleskop på La Palma, på De Kanariske Øer, bruger et primært parabolsk spejl til at reflektere lys mod et sekundært hyperbolsk spejl, som afspejler det igen til et fokus bag det første spejl.

I det virkelige projektive plan

De keglesnit har nogle meget lignende egenskaber i det euklidiske plan, og årsagerne hertil bliver tydeligere, når keglerne ses fra en større geometri. Det euklidiske plan kan være indlejret i det virkelige projektive plan, og keglerne kan betragtes som objekter i denne projektive geometri. En måde at gøre dette på er at indføre homogene koordinater og definere en kegle til at være det sæt af punkter, hvis koordinater tilfredsstiller en ureducerbar kvadratisk ligning i tre variabler (eller ækvivalent nulerne i en irreducerbar kvadratisk form ). Mere teknisk kaldes det sæt punkter, der er nuller af en kvadratisk form (i et hvilket som helst antal variabler) en quadric , og de irreducerbare quadrics i et todimensionelt projektivt rum (det vil sige at have tre variabler) kaldes traditionelt kegler.

Euklidisk plan R ² er indlejret i den virkelige projektiv plan ved tilstødende en linie ved uendelig (og dens tilsvarende punkter uendelig langt ), således at alle linjerne i en parallel klasse mødes på denne linje. På den anden side, ved at starte med det virkelige projektive plan, opnås et euklidisk plan ved at skelne en linje som linjen i det uendelige og fjerne det og alle dets punkter.

Skæringspunkt i det uendelige

I et projektivt rum over enhver divisionsring, men især over enten de reelle eller komplekse tal, er alle ikke-degenererede kegler ækvivalente, og således taler man i projektiv geometri simpelthen om "en kegle" uden at specificere en type. Det vil sige, at der er en projektiv transformation, der vil kortlægge enhver ikke-degenereret kegle til enhver anden ikke-degenereret kegle.

De tre typer keglesnit vil igen dukke op i affineplanet opnået ved at vælge en linje i det projektive rum til at være linjen i det uendelige. De tre typer bestemmes derefter af, hvordan denne linje i det uendelige skærer keglen i det projektive rum. I det tilsvarende affinerum opnår man en ellipse, hvis keglen ikke skærer linjen ved uendelig, en parabel, hvis keglen skærer linjen ved uendeligt i et dobbeltpunkt svarende til aksen, og en hyperbola, hvis keglen skærer linjen ved uendelig i to punkter svarende til asymptoterne.

Homogene koordinater

I homogene koordinater kan et keglesnit repræsenteres som:

${\ displaystyle Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2} = 0.}$

Eller i matrix notation

${\ displaystyle \ left ({\ begin {matrix} x & y & z \ end {matrix}} \ right) \ left ({\ begin {matrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \ end {matrix}} \ right) \ left ({\ begin {matrix} x \\ y \\ z \ end {matrix}} \ right) = 0.}$

3 × 3 -matrixen ovenfor kaldes matricen for den keglesnit .

Nogle forfattere foretrækker at skrive den generelle homogene ligning som

${\ displaystyle Ax^{2}+2Bxy+Cy^{2}+2Dxz+2Eyz+Fz^{2} = 0,}$

(eller en variation af dette), så matricen i det keglesnit har den enklere form,

${\ displaystyle M = \ left ({\ begin {matrix} A & B & D \\ B & C & E \\ D & E & F \ end {matrix}} \ right),}$

men denne notation bruges ikke i denne artikel.

Hvis determinanten for matricen i det keglesnit er nul, degenereres det keglesnit .

Når man multiplicerer alle seks koefficienter med den samme ikke-nul-skalar giver en ligning med det samme sæt nuller, kan man betragte kegler, repræsenteret med ( A , B , C , D , E , F ) som punkter i det femdimensionale projektive plads ${\ displaystyle \ mathbf {P} ^{5}.}$

Projektiv definition af en cirkel

Metriske begreber i euklidisk geometri (begreber, der vedrører måling af længder og vinkler) kan ikke umiddelbart udvides til det virkelige projektive plan. De skal redefineres (og generaliseres) i denne nye geometri. Dette kan gøres for vilkårlige projektive fly , men for at opnå det virkelige projektive plan som det udvidede euklidiske plan, skal der træffes nogle specifikke valg.

Fix en vilkårlig linje i et projektionsplan, der skal betegnes som den absolutte linje . Vælg to forskellige punkter på den absolutte linje og betegne dem som absolutte punkter . Flere metriske begreber kan defineres med henvisning til disse valg. For eksempel givet en linje, der indeholder punkterne A og B , den midtpunktet af linjestykket AB er defineret som det punkt C, som er den projektiv harmoniske konjugat af skæringspunktet af AB og den absolutte linje med hensyn til A og B .

En kegle i et projektionsplan, der indeholder de to absolutte punkter, kaldes en cirkel . Da fem punkter bestemmer en kegle, bestemmes en cirkel (som kan være degenereret) af tre punkter. For at opnå det udvidede euklidiske plan vælges den absolutte linje til at være linjen ved uendeligt af det euklidiske plan, og de absolutte punkter er to specielle punkter på den linje kaldet cirkulære punkter ved uendelig . Linjer, der indeholder to punkter med reelle koordinater, passerer ikke gennem de cirkulære punkter i det uendelige, så i det euklidiske plan bestemmes en cirkel under denne definition af tre punkter, der ikke er kollinære .

Det er blevet nævnt, at cirkler i det euklidiske plan ikke kan defineres af fokus-directrix-egenskaben. Men hvis man skulle betragte linjen i det uendelige som directrix, så ved at tage excentriciteten til at være e = 0 vil en cirkel have focus-directrix-egenskaben, men den er stadig ikke defineret af den egenskab. Man skal være forsigtig i denne situation for korrekt at bruge definitionen af ​​excentricitet som forholdet mellem afstanden af ​​et punkt på cirklen til fokus (radiuslængde) til afstanden fra dette punkt til directrix (denne afstand er uendelig) hvilket giver grænseværdien på nul.

Steiners projektive koniske definition

En syntetisk (koordinatfri) tilgang til at definere de keglesnit i et projektivt plan blev givet af Jakob Steiner i 1867.

• Givet to blyanter af linjer på to punkter (alle linjer indeholdende og hhv.) Og en projektiv, men ikke perspektivisk kortlægning af på . Derefter danner skæringspunkterne for de tilsvarende linjer et ikke-degenereret projektivt keglesnit.${\ displaystyle B (U), B (V)}$${\ displaystyle U, V}$${\ displaystyle U}$${\ displaystyle V}$${\ displaystyle \ pi}$${\ displaystyle B (U)}$${\ displaystyle B (V)}$

En perspektivisk kortlægning af en blyant på en blyant er en bijektion (1-1 korrespondance) sådan, at tilsvarende linjer skærer hinanden på en fast linje , som kaldes perspektivitetens akse . ${\ displaystyle \ pi}$${\ displaystyle B (U)}$${\ displaystyle B (V)}$${\ displaystyle a}$${\ displaystyle \ pi}$

En projektiv kortlægning er en begrænset række af perspektiviske kortlægninger.

Som en projekterende kortlægning i et projektivt plan over et felt ( pappianplan ) er entydigt bestemt ved at foreskrive billederne af tre linjer, for Steiner -generationen af ​​et keglesnit skal der udover to punkter kun gives billeder af 3 linjer. Disse 5 punkter (2 punkter, 3 linjer) bestemmer entydigt det keglesnit. ${\ displaystyle U, V}$

Linjekegler

Ved dualitetsprincippet i et projektivt plan er dual af hvert punkt en linje, og dual af et locus af punkter (et sæt punkter, der opfylder en eller anden betingelse) kaldes en konvolut af linjer. Ved at bruge Steiners definition af en kegle (dette punkt af punkter vil nu blive omtalt som en punktkegle ) som mødet af tilsvarende stråler fra to beslægtede blyanter, er det let at dualisere og opnå den tilsvarende kuvert bestående af sammenføjninger af tilsvarende punkter af to relaterede områder (punkter på en linje) på forskellige baser (de linjer, punkterne er på). En sådan konvolut kaldes en linjekegle (eller dobbeltkegle ).

I det virkelige projektive plan har en punktkegle den egenskab, at hver linje møder den i to punkter (som kan falde sammen eller kan være kompleks), og ethvert sæt punkter med denne egenskab er en punktkegle. Det følger dobbelt, at en linjekegle har to af sine linjer gennem hvert punkt, og enhver konvolut af linjer med denne egenskab er en linjekegle. På hvert punkt i en punktkegle er der en unik tangentlinje, og på hver linje i en linjekegle er der et unikt punkt kaldet et kontaktpunkt . En vigtig sætning siger, at tangentlinjerne i en punktkegle danner en linjekegle, og dualt udgør kontaktpunkterne for en linjekegle en punktkegle.

Von Staudts definition

Karl Georg Christian von Staudt definerede en kegle som det punkt, der blev givet af alle absolutte punkter i en polaritet, der har absolutte punkter. Von Staudt introducerede denne definition i Geometrie der Lage (1847) som en del af sit forsøg på at fjerne alle metriske begreber fra projektiv geometri.

En polaritet , π , af et projektionsplan, P , er en ufrivillig (dvs. af rækkefølge to) bijektion mellem punkterne og linjerne i P, der bevarer forekomsten . Således er en polaritet angår et punkt Q med en linje q og efter Gergonne , q kaldes polære af Q og Q den pol af q . Et absolut punkt ( linje ) i en polaritet er et, der hænger sammen med dets polar (pol).

En von Staudt -kegle i det virkelige projektive plan svarer til en Steiner -kegle .

Konstruktioner

Ingen kontinuerlig bue af en kegle kan konstrueres med straightedge og kompas. Der er imidlertid flere opretnings-og-kompas-konstruktioner til et vilkårligt antal individuelle punkter på en bue.

En af dem er baseret på det modsatte af Pascals sætning, nemlig hvis skæringspunkterne for modsatte sider af en sekskant er kollinære, så ligger de seks hjørner på en kegle. Specifikt givet fem punkter, A , B , C , D , E og en linje, der går gennem E , siger EG , kan et punkt F, der ligger på denne linje og er på keglen bestemt af de fem punkter, konstrueres. Lad AB mødes DE i L , BC mødes EG i M og lad CD mødes LM på N . Så AN møder EG på det krævede tidspunkt F . Ved at variere linjen gennem E kan der konstrueres så mange yderligere punkter på keglen som ønsket.

En anden metode, der er baseret på Steiners konstruktion, og som er nyttig i tekniske applikationer, er parallelogrammetoden , hvor en kegle konstrueres punkt for punkt ved at forbinde visse lige store punkter på en vandret linje og en lodret linje. Specifikt at konstruere ellipsen med ligningx ²/a ² + y ²/b ²= 1 , konstruer først rektanglet ABCD med hjørner A ( a , 0), B ( a , 2 b ), C ( - a , 2 b ) og D ( - a , 0) . Opdel siden BC i n lige store segmenter og brug parallel projektion i forhold til den diagonale AC for at danne lige segmenter på side AB (længderne på disse segmenter vil væreb/-engange længden af ​​segmenterne på BC ). På siden BC etiketten Den venstre endepunkter af segmenterne med A ₁ til A _n begyndende ved B og går i retning C . På den side AB mærke de øvre endepunkter D ₁ til D _n begyndende ved A og går i retning B . Skæringspunkterne, AA _i ∩ DD _i for 1 ≤ i ≤ n vil være ellipsens punkter mellem A og P (0, b ) . Mærkningen forbinder blyantens linjer gennem A med blyantens linjer gennem D projektivt, men ikke perspektivisk. Det søgt efter kegle opnås ved denne konstruktion, da tre punkter A , D og P og to tangenter (de lodrette linjer ved A og D ) entydigt bestemmer keglen. Hvis der bruges en anden diameter (og dens konjugerede diameter) i stedet for ellipsens større og mindre akser, bruges et parallelogram, der ikke er et rektangel, i konstruktionen, der giver navnet på metoden. Sammenslutningen af ​​blyanter kan forlænges for at opnå andre punkter på ellipsen. Konstruktionerne for hyperboler og paraboler ligner hinanden.

Endnu en anden generel metode anvender polaritetsegenskaben til at konstruere tangenshylsteret af en kegle (en linjekegle).

I det komplekse projektive plan

I det komplekse plan C ² er ellipser og hyperboler ikke forskellige: man kan betragte en hyperbola som en ellipse med en imaginær akselængde. For eksempel bliver ellipsen en hyperbola under substitutionen geometrisk en kompleks rotation, der giver . Der er således en 2-vejs klassifikation: ellipse/hyperbola og parabel. Ved at forlænge kurverne til det komplekse projektive plan svarer dette til at krydse linjen ved uendeligt i enten 2 forskellige punkter (svarende til to asymptoter) eller i 1 dobbeltpunkt (svarende til en parabols akse); således er den virkelige hyperbola et mere suggestivt virkeligt billede for den komplekse ellipse/hyperbola, da den også har 2 (reelle) skæringspunkter med linjen i det uendelige. ${\ displaystyle x^{2}+y^{2} = 1}$${\ displaystyle y = iw,}$${\ displaystyle x^{2} -w^{2} = 1}$

Yderligere forening sker i det komplekse projektive plan CP ² : de ikke-degenererede kegler kan ikke skelnes fra hinanden, da enhver kan føres til enhver anden ved en projektiv lineær transformation .

Det kan bevises, at i CP ² har to keglesnit fire punkter til fælles (hvis en tegner sig for multiplicitet ), så der er mellem 1 og 4 skæringspunkter . Skæringsmulighederne er: fire forskellige punkter, to entallspunkter og et dobbeltpunkt, to dobbeltpunkter, et entalpunkt og et med multiplicitet 3, et punkt med multiplicitet 4. Hvis et skæringspunkt har multiplicitet> 1, siges de to kurver at være tangent . Hvis der er et skæringspunkt med multiplicitet mindst 3, siges de to kurver at være osculerende . Hvis der kun er et skæringspunkt, som har multiplicitet 4, siges de to kurver at være superoskulerende .

Desuden skærer hver lige linje hver keglesnit to gange. Hvis skæringspunktet er dobbelt, er linjen en tangentlinje . Krydsende med linjen i det uendelige, har hvert keglesnit to punkter i det uendelige. Hvis disse punkter er reelle, er kurven en hyperbola ; hvis de er imaginære konjugater, er det en ellipse ; hvis der kun er et dobbeltpunkt, er det en parabel . Hvis punkterne i det uendelige er de cykliske punkter (1, i , 0) og (1, - i , 0) , er det keglesnit en cirkel . Hvis koefficienterne i et keglesnit er reelle, er punkterne ved uendelig enten reelle eller komplekse konjugater .

Degenererede tilfælde

Hvad der skal betragtes som et degenereret tilfælde af en kegle afhænger af den definition, der bruges, og den geometriske indstilling for den keglesnit. Der er nogle forfattere, der definerer en kegle som en todimensionel ikke-degenereret quadric. Med denne terminologi er der ingen degenererede kegler (kun degenererede quadrics), men vi skal bruge den mere traditionelle terminologi og undgå den definition.

I euklidisk plan, ved hjælp af geometriske definition, opstår der et degenereret tilfælde, hvor skæreplanet passerer gennem toppunktet af keglen. Den degenererede kegle er enten: et punkt , når flyet kun skærer keglen ved spidsen; en lige linje , når planet er tangent til keglen (den indeholder nøjagtigt en generator af keglen); eller et par krydsende linjer (to generatorer af keglen). Disse svarer henholdsvis til de begrænsende former for en ellipse, parabel og en hyperbola.

Hvis en kegle i det euklidiske plan defineres af nullerne i en kvadratisk ligning (det vil sige som en kvadrik), så er de degenererede kegler: det tomme sæt , et punkt eller et par linjer, der kan være parallelle, skærer hinanden på et tidspunkt eller sammenfaldende. Det tomme sæt tilfælde kan enten svare til et par komplekse konjugerede parallelle linjer såsom med ligningen eller en imaginær ellipse , f.eks. Med ligningen En imaginær ellipse opfylder ikke den generelle definition af en degeneration , og betragtes derfor normalt ikke som degenereret. De to linjers tilfælde opstår, når de kvadratiske udtryksfaktorer inddeles i to lineære faktorer, hvor nulerne hver giver en linje. I det tilfælde, at faktorerne er de samme, falder de tilsvarende linjer sammen, og vi refererer til linjen som en dobbeltlinje (en linje med multiplicitet 2), og dette er det tidligere tilfælde af et tangentskæringsplan. ${\ displaystyle x^{2}+1 = 0,}$${\ displaystyle x^{2}+y^{2}+1 = 0.}$

I det virkelige projektive plan, da parallelle linjer mødes på et punkt på linjen i det uendelige, kan det parallelle linies tilfælde af det euklidiske plan ses som krydsende linjer. Men da skæringspunktet er keglens spids, degenererer selve keglen til en cylinder , altså med spidsen i det uendelige. Andre sektioner i dette tilfælde kaldes cylindriske sektioner . De ikke-degenererede cylindriske sektioner er ellipser (eller cirkler).

Set fra perspektivet af det komplekse projektive plan kan de degenererede tilfælde af en reel kvadrik (dvs. den kvadratiske ligning har reelle koefficienter) alle betragtes som et par linjer, der muligvis er sammenfaldende. Det tomme sæt kan være linjen i det uendelige betragtet som en dobbelt linje, et (reelt) punkt er skæringspunktet mellem to komplekse konjugerede linjer og de andre tilfælde som tidligere nævnt.

For at skelne de degenererede sager fra ikke-degenererede sager (herunder den tomme sæt med sidstnævnte) under anvendelse matricenotationen, lad β være determinanten af 3 × 3 matrix keglesnit-dvs. β = ( AC -B ²/4) F +SENG - CD ² - AE ²/4; og lad α = B ² - 4 AC være diskriminerende. Så er det keglesnit ikke-degenereret, hvis og kun hvis β ≠ 0 . Hvis β = 0 har vi et punkt, når α <0 , to parallelle linjer (muligvis sammenfaldende) når α = 0 eller to skærende linjer, når α > 0 .

Blyant af kegler

En (ikke-degenereret) kegle bestemmes fuldstændigt af fem punkter i den generelle position (ingen tre kollinære ) i et plan, og systemet med kegler, der passerer gennem et fast sæt på fire punkter (igen i et plan og ikke tre kollinear) kaldes en blyant af kegler . De fire fælles punkter kaldes blyantens basispunkter . Gennem et andet punkt end et basispunkt passerer der en enkelt kegle af blyanten. Dette koncept generaliserer en blyant af cirkler .

Kryds to kegler

Løsningerne til et system med to andengradsligninger i to variabler kan ses som koordinaterne for skæringspunkterne mellem to generiske keglesnit. Især to kegler kan ikke besidde ingen, to eller fire muligvis sammenfaldende skæringspunkter. En effektiv metode til at lokalisere disse løsninger udnytter den homogene matrixrepræsentation af keglesnit , dvs. en 3 × 3 symmetrisk matrix, der afhænger af seks parametre.

Proceduren for at lokalisere skæringspunkterne følger disse trin, hvor keglerne repræsenteres af matricer:

• i betragtning af de to kegler og overveje kegleblyanten givet af deres lineære kombination${\ displaystyle C_ {1}}$${\ displaystyle C_ {2}}$${\ displaystyle \ lambda C_ {1}+\ mu C_ {2}.}$
• identificere de homogene parametre, der svarer til blyantens degenererede kegle. Dette kan gøres ved at pålægge betingelsen det og løse for og . Disse viser sig at være løsningerne i en tredjegradsligning.${\ displaystyle (\ lambda, \ mu)}$${\ displaystyle \ det (\ lambda C_ {1}+\ mu C_ {2}) = 0}$${\ displaystyle \ lambda}$${\ displaystyle \ mu}$
• givet den degenererede kegle , identificer de to, muligvis sammenfaldende, linjer, der udgør den.${\ displaystyle C_ {0}}$
• skærer hver identificeret linje med en af ​​de to originale kegler; dette trin kan udføres effektivt ved hjælp af den dobbelte koniske repræsentation af${\ displaystyle C_ {0}}$
• skæringspunkterne vil repræsentere løsningerne til det oprindelige ligningssystem.

Generaliseringer

Kegler kan defineres over andre felter (det vil sige i andre pappiske geometrier ). Dog skal der bruges en vis forsigtighed, når feltet har karakteristik 2, da nogle formler ikke kan bruges. For eksempel kræver matrixrepræsentationer, der er brugt ovenfor , division med 2.

En generalisering af en ikke-degenereret kegle i et projektionsplan er en oval . En oval er et punktmængde, der har følgende egenskaber, som holdes af kegler: 1) enhver linje skærer en oval i ingen, et eller to punkter, 2) på et hvilket som helst punkt i ovalen eksisterer der en unik tangentlinje.

Generalisering af koniske egenskaber ved kegler til det tilfælde, hvor der er mere end to foci, producerer sæt kaldet generaliserede kegler .

På andre områder af matematik

Klassificeringen i elliptisk, parabolsk og hyperbolsk er gennemgående i matematik og deler ofte et felt i skarpt adskilte underfelter. Klassifikationen opstår for det meste på grund af tilstedeværelsen af ​​en kvadratisk form (i to variabler svarer dette til den tilhørende diskriminant ), men kan også svare til excentricitet.

Klassificeringer i kvadratisk form:

Kvadratiske former

Kvadratiske former over realerne er klassificeret efter Sylvesters inertilov , nemlig efter deres positive indeks, nulindeks og negative indeks: en kvadratisk form i n variabler kan konverteres til en diagonal form , som hvor antallet af +1 koefficienter, k , er det positive indeks, antallet af -1 koefficienter, ℓ , er det negative indeks, og de resterende variabler er nulindekset m, så I to variabler klassificeres de ikke-nul kvadratiske former som: ${\ displaystyle x_ {1}^{2}+x_ {2}^{2}+\ cdots+x_ {k}^{2} -x_ {k+1}^{2}-\ cdots -x_ {k+ \ ell}^{2},}$${\ displaystyle k +\ ell +m = n.}$

• ${\ displaystyle x^{2}+y^{2}}$ -positiv-bestemt (det negative er også inkluderet), svarende til ellipser,
• ${\ displaystyle x^{2}}$ - degenereret, svarende til paraboler, og
• ${\ displaystyle x^{2} -y^{2}}$ - ubestemt, svarende til hyperboler.

I to variabler klassificeres kvadratiske former efter diskriminant, analogt med kegler, men i højere dimensioner er den mere nyttige klassifikation som bestemt, (alle positive eller alle negative), degenererede, (nogle nuller) eller ubestemt (blanding af positivt og negativt, men ingen nuller). Denne klassificering ligger til grund for mange, der følger.

Krumning

Den gaussiske krumning af en overflade beskriver infinitesimale geometri og kan i hvert punkt være enten positiv - elliptisk geometri , nul - euklidisk geometri (flad, parabel), eller negativ - hyperbolsk geometri ; uendeligt, til anden ordens overflade ligner grafen for (eller 0) eller . Ved uniformeringsteoremet kan hver overflade faktisk anses for at være globalt (på ethvert tidspunkt) positivt buet, fladt eller negativt buet. I højere dimensioner er Riemann -krumningstensoren et mere kompliceret objekt, men manifolder med konstant snitkurvatur er interessante undersøgelsesobjekter og har påfaldende forskellige egenskaber, som diskuteret ved snitkurvatur .${\ displaystyle x^{2}+y^{2},}$ ${\ displaystyle x^{2}}$${\ displaystyle x^{2} -y^{2}}$

Anden ordens PDE'er

Partielle differentialligninger (PDE'er) af anden orden klassificeres på hvert tidspunkt som elliptisk, parabolsk eller hyperbolsk, følgelig som deres andenordens udtryk svarer til en elliptisk, parabolsk eller hyperbolsk kvadratisk form. Opførslen og teorien for disse forskellige typer PDE'er er påfaldende forskellige - repræsentative eksempler er, at Poisson -ligningen er elliptisk, varme -ligningen er parabolsk, og bølge -ligningen er hyperbolsk.

Eccentricity -klassifikationer omfatter:

Möbius -transformationer

Ægte Möbius-transformationer (elementer i PSL ₂ ( R ) eller dets 2-foldede dæksel, SL ₂ ( R ) ) klassificeres som elliptisk, parabolsk eller hyperbolsk i overensstemmelse hermed, da deres halvspor er eller afspejler klassificeringen efter excentricitet.${\ displaystyle 0 \ leq | \ operatorname {tr} |/2 <1,}$ ${\ displaystyle | \ operatorname {tr} |/2 = 1,}$${\ displaystyle | \ operatorname {tr} |/2> 1,}$

Variance-to-mean ratio

Varians-til-middel-forholdet klassificerer flere vigtige familier af diskrete sandsynlighedsfordelinger : den konstante fordeling som cirkulær (excentricitet 0), binomiske fordelinger som elliptiske, Poisson-fordelinger som parabolske og negative binomiale fordelinger som hyperboliske. Dette er uddybet ved kumulanter af nogle diskrete sandsynlighedsfordelinger .

Se også

• Omkringelig og inkonisk
• Conic Sections Rebellion , protester fra Yale universitetsstuderende
• Direktørkreds
• Elliptisk koordinatsystem
• Ensartet sæt
• Ni-punkts kegle
• Paraboliske koordinater
• Kvadratisk funktion
• Sfærisk kegle

Noter

Referencer

Bibliografi

• Akopyan, AV; Zaslavsky, AA (2007). Conics geometri . American Mathematical Society . ISBN 978-0-8218-4323-9.
• Artzy, Rafael (2008) [1965], Lineær geometri , Dover, ISBN 978-0-486-46627-9
• Boyer, Carl B. (2004) [1956], History of Analytic Geometry , Dover, ISBN 978-0-486-43832-0
• Brannan, David A .; Esplen, Matthew F .; Gray, Jeremy J. (1999), Geometry , Cambridge University Press, ISBN 978-0-521-59787-6
• Coxeter, HSM (1964), Projective Geometry , Blaisdell, ISBN 9780387406237
• Coxeter, HSM (1993), The Real Projective Plane , Springer Science & Business Media
• Downs, JW (2003) [1993], Practical Conic Sections: De geometriske egenskaber ved ellipse, parabol og hyperbola , Dover, ISBN 0-486-42876-1
• Eves, Howard (1963), A Survey of Geometry (Volume One) , Boston: Allyn og Bacon
• Glaeser, Georg; Stachel, Hellmuth; Odehnal, Boris (2016), The Universe of Conics: Fra de gamle grækere til det 21. århundredes udvikling , Berlin: Springer
• Hartmann, Erich, Planar Circle Geometries, an Introduction to Moebius-, Laguerre- og Minkowski Planes (PDF) , hentet 20. september 2014 (PDF; 891 kB).
• Katz, Victor J. (1998), A History of Mathematics / An Introduction (2. udgave), Addison Wesley Longman, ISBN 978-0-321-01618-8
• Kendig, Keith (2005), Conics , The Mathematical Association of America , ISBN 978-0-88385-335-1
• Faulkner, TE (1952), Projective Geometry (2. udgave), Edinburgh: Oliver og Boyd, ISBN 9780486154893
• Merserve, Bruce E. (1983) [1959], Fundamental Concepts of Geometry , Dover, ISBN 0-486-63415-9
• Protter, Murray H .; Morrey, Jr., Charles B. (1970), College Calculus with Analytic Geometry (2. udgave), Reading: Addison-Wesley , LCCN  76087042
• Richter-Gebert, Jürgen (2011). Perspektiver på projektiv geometri: En guidet tur gennem reel og kompleks geometri . Springer. ISBN 9783642172854.
• Samuel, Pierre (1988), Projective Geometry , Undergraduate Texts in Mathematics (Readings in Mathematics), New York: Springer-Verlag, ISBN 0-387-96752-4
• Thomas, George B .; Finney, Ross L. (1979), Calculus and Analytic Geometry (femte udgave), Addison-Wesley, s. 434, ISBN 0-201-07540-7
• Wilson, WA; Tracey, JI (1925), Analytic Geometry (Revideret red.), DC Heath and Company

eksterne links

• Kan du virkelig udlede kegleformler fra en kegle? arkiv 2007-07-15 Gary S. Stoudt ( Indiana University of Pennsylvania
• Keglesnit ved specielle flykurver .
• Weisstein, Eric W. "Keglesnit" . MathWorld .
• Forekomst af kegler. Kegler i naturen og andre steder .
• Se Conic Sections på cut-the-knot for et skarpt bevis på, at enhver endelig keglesnit er en ellipse og Xah Lee til en lignende behandling af andre kegler.
• Otte punktskegle ved dynamiske geometri skitser
• Andenordens implicitte ligningslokal En interaktiv Java-konisk graf; bruger en generel andenordens implicit ligning.