Matematisk konstant - Mathematical constant

En matematisk konstant er et centralt nummer , hvis værdi er fastsat af en entydig definition af et symbol (f.eks en ofte omtalt alfabet bogstav ), eller ved matematikere navne for at lette at bruge det på tværs af flere matematiske problemer . Konstanter opstår på mange områder af matematik , hvor konstanter som $e$ og $π$ forekommer i så forskellige sammenhænge som geometri , talteori og beregning .

Hvad det betyder for en konstant at opstå "naturligt", og hvad der gør en konstant "interessant", er i sidste ende et spørgsmål om smag, hvor nogle matematiske konstanter er mere bemærkelsesværdige af historiske årsager end af deres iboende matematiske interesse. De mere populære konstanter er blevet undersøgt gennem tiderne og beregnet til mange decimaler.

Alle navngivne matematiske konstanter er definerbare tal og er normalt også beregningsbare tal ( Chaitins konstant er en væsentlig undtagelse).

Grundlæggende matematiske konstanter

Disse er konstanter, som man sandsynligvis vil støde på under førskoleundervisning i mange lande.

Archimedes 'konstante $π$

Omkredsen af en cirkel med diameter 1 er

π

.

Den konstante $π$ (pi) har en naturlig definition i euklidisk geometri som forholdet mellem omkreds og diameter af en cirkel. Det kan findes mange andre steder i matematik: for eksempel den gaussiske integral , enhedens komplekse rødder og Cauchy -fordelinger i sandsynlighed . Imidlertid er dens allestedsnærværende ikke begrænset til ren matematik. Det forekommer i mange formler i fysik, og flere fysiske konstanter er mest naturligt defineret med $π$ eller dets gensidige indregnet. For eksempel grundtilstanden bølge funktion af hydrogen atom er

{\ displaystyle \ psi (\ mathbf {r}) = {\ frac {1} {(\ pi a_ {0}^{3})^{1/2}}} e^{-r/a_ {0} },}

hvor er Bohr -radius . ${\ displaystyle a_ {0}}$

$π$ er et irrationelt tal .

Den numeriske værdi af $π$ er cirka 3,1415926536 (sekvens A000796 i OEIS ). At huske stadig mere præcise cifre på $π$ er en verdensrekordforfølgelse.

Den imaginære enhed $i$

Den imaginære enhed

i

i det komplekse plan . Reelle tal ligger på den vandrette akse, og imaginære tal ligger på den lodrette akse

Den imaginære enhed eller enhed imaginære tal , betegnet som $i$ , er et matematisk begreb, der udvider det reelle talssystem til det komplekse talsystem Den imaginære enheds kerneegenskab er, at $i$ $2$ $= -1$ . Udtrykket " imaginær " blev opfundet, fordi der ikke er et ( reelt ) tal, der har en negativ firkant . ${\ displaystyle \ mathbb {R}}$ ${\ displaystyle \ mathbb {C}.}$

Der er faktisk to komplekse kvadratrødder af −1, nemlig $i$ og $- i$ , ligesom der er to komplekse kvadratrødder for hvert andet reelt tal (undtagen nul , som har en dobbelt kvadratrod).

I sammenhænge, hvor symbolet $i$ er tvetydigt eller problematisk, bruges $j$ eller den græske jota ( $ι$ ) nogle gange. Dette er især tilfældet inden for elektroteknik og kontrolsystemteknik , hvor den imaginære enhed ofte betegnes med $j$ , fordi $i$ almindeligvis bruges til at betegne elektrisk strøm .

Eulers nummer $e$

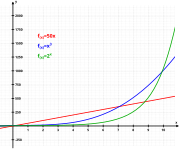
Eksponentiel vækst (grøn) beskriver mange fysiske fænomener.

Eulers nummer $e$ , også kendt som den eksponentielle vækstkonstant , optræder i mange matematikområder, og en mulig definition af det er værdien af følgende udtryk:

{\ displaystyle e = \ lim _ {n \ til \ infty} \ venstre (1+{\ frac {1} {n}} \ højre)^{n}}

Konstanten $e$ er i sagens natur relateret til den eksponentielle funktion . ${\ displaystyle x \ mapsto e^{x}}$

Den schweiziske matematiker Jacob Bernoulli opdagede, at $e$ opstår i rentesatser : Hvis en konto starter ved $ 1 og giver renter med en årlig sats $R$ , da antallet af sammensætningsperioder om året har tendens til uendelig (en situation kendt som kontinuerlig sammensætning ), vil beløb i slutningen af året vil nærme sig $e R$ dollars.

Den konstante $e har$ også anvendelser til sandsynlighedsteori , hvor den opstår på en måde, der ikke åbenbart er relateret til eksponentiel vækst. Antag som et eksempel, at en spilleautomat med en i $n$ sandsynlighed for at vinde spilles $n$ gange, så for store $n$ (f.eks. En million) vil sandsynligheden for, at intet vil blive vundet, have en tendens til $1/ e,$ som $n$ har tendens til uendelighed.

En anden anvendelse af $e$ , der delvis blev opdaget af Jacob Bernoulli sammen med den franske matematiker Pierre Raymond de Montmort , er i problemet med forstyrrelser , også kendt som hat -check -problemet . Her inviteres $n$ gæster til en fest, og ved døren tjekker hver gæst sin hat med butleren, som derefter placerer dem i mærkede kasser. Butleren kender ikke gæsternes navn og skal derfor lægge dem i bokse, der er valgt tilfældigt. Problemet med de Montmort er: hvad er sandsynligheden for, at ingen af hatte kommer i den rigtige boks. Svaret er

{\ displaystyle p_ {n} = 1-{\ frac {1} {1!}}+{\ frac {1} {2!}}-{\ frac {1} {3!}}+\ cdots+( -1)^{n} {\ frac {1} {n!}}}

der, som $n$ har tendens til uendelig, nærmer sig $1/ e$ .

$e$ er et irrationelt tal .

Den numeriske værdi af $e$ er cirka 2,7182818284 (sekvens A001113 i OEIS ).

Pythagoras konstant $\sqrt 2$

Kvadratroden af 2 er lig med længden af hypotenusen i en retvinklet trekant med ben i længden 1.

Den kvadratroden af 2 , ofte kendt som roden 2 , radikal 2 , eller Pythagoras' konstant , og skrives som $\sqrt 2$ , er det positivt algebraiske tal , at når ganget med sig selv, giver det nummer 2 . Det kaldes mere præcist hovedkvadratroden af 2 for at skelne det fra det negative tal med den samme egenskab.

Geometrisk er kvadratroden af 2 længden af en diagonal på tværs af en firkant med sider af en længdeenhed ; dette følger af Pythagoras sætning . Det var sandsynligvis det første tal, der var kendt for at være irrationelt . Dens numeriske værdi afkortet til 65 decimaler er:

1,41421 35.623 73095 04.880 16887 24.209 69.807 85.696 71.875 37.694 80.731 76.679 73.799 ... (sekvens A002193 i OEIS ).

Kvadratroden af 2.

Alternativt blev den hurtige tilnærmelse 99/70 (≈ 1.41429) til kvadratroden af to ofte brugt før almindelig brug af elektroniske lommeregnere og computere . På trods af at den kun har en nævner på 70, adskiller den sig fra den korrekte værdi med mindre end 1/10.000 (ca. 7,2 × 10 ⁻⁵ ).

Theodorus konstant $\sqrt 3$

Den numeriske værdi af $\sqrt 3$ er cirka 1,7320508075 (sekvens A002194 i OEIS ).

Konstanter i avanceret matematik

Disse er konstanter, som ofte findes i højere matematik .

Feigenbaum -konstanterne α og δ

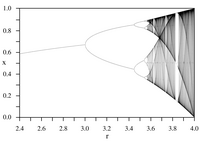
Bifurcationsdiagram over det logistiske kort.

Iterationer af kontinuerlige kort fungerer som de enkleste eksempler på modeller til dynamiske systemer . Opkaldt efter matematisk fysiker Mitchell Feigenbaum optræder de to Feigenbaum -konstanter i sådanne iterative processer: de er matematiske invarianter af logistiske kort med kvadratiske maksimumspunkter og deres todelt diagrammer .

Det logistiske kort er en polynomisk kortlægning, der ofte nævnes som et arketypisk eksempel på, hvordan kaotisk adfærd kan opstå fra meget simple ikke-lineære dynamiske ligninger. Kortet blev populariseret i et skelsættende papir fra 1976 af den australske biolog Robert May , dels som en diskret tid demografisk model analog med den logistiske ligning, der først blev skabt af Pierre François Verhulst . Differensligningen er beregnet til at fange de to effekter af reproduktion og sult.

Den numeriske værdi af α er cirka 2,5029. Den numeriske værdi af δ er cirka 4.6692.

Apérys konstante ζ (3)

Aperys konstant er summen af serien

{\ displaystyle \ zeta (3) = 1+{\ frac {1} {2^{3}}}+{\ frac {1} {3^{3}}}+{\ frac {1} {4^ {3}}}+\ cdots}

Apérys konstant er et irrationelt tal, og dens numeriske værdi er cirka 1,2020569.

Trods en særlig værdi af riemanns zetafunktion opstår apérys konstant naturligt i en række fysiske problemer, herunder i anden og tredje ordens led af elektron 's gyromagnetiske forhold , beregnet ved hjælp kvanteelektrodynamik .

Det gyldne snit $φ$

Gyldne rektangler i en almindelig icosahedron

{\ displaystyle F_ {n} = {\ frac {\ varphi ^{n}-(1- \ varphi) ^{n}} {\ sqrt {5}}}}

En eksplicit formel for

n

th Fibonacci nummer involverer gyldne snit

φ

.

Tallet $φ$ , også kaldet det gyldne snit , dukker ofte op i geometri , især i figurer med femkantet symmetri . Faktisk længden af en regulær femkant 's diagonal er $cp$ gange sin side. Hjørnerne af en almindelig icosahedron er de af tre indbyrdes ortogonale gyldne rektangler . Det vises også i Fibonacci -sekvensen , relateret til vækst ved rekursion . Kepler beviste, at det er grænsen for forholdet mellem på hinanden følgende Fibonacci -tal. Det gyldne snit har den langsomste konvergens af ethvert irrationelt tal. Det er af den grund et af de værste tilfælde af Lagranges tilnærmelse -sætning, og det er et ekstremt tilfælde af Hurwitz -uligheden for Diophantine -tilnærmelser . Dette kan være grunden til, at vinkler tæt på det gyldne snit ofte viser sig i phyllotaxis (plantens vækst). Det er omtrent lig med 1.6180339887498948482, eller mere præcist 2⋅sin (54 °) = ${\ displaystyle \ scriptstyle {\ frac {1+{\ sqrt {5}}} {2}}.}$

Euler – Mascheroni -konstanten y

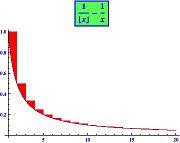
Området mellem de to kurver (rødt) har en tendens til en grænse, nemlig Euler-Mascheroni-konstanten.

Den Euler-Mascheroni konstant er defineret som grænsen følgende:

{\ displaystyle {\ begin {align} \ gamma & = \ lim _ {n \ to \ infty} \ left (\ left (\ sum _ {k = 1}^{n} {\ frac {1} {k} } \ højre)-\ ln n \ højre) \\ [5px] \ end {justeret}}}

Euler – Mascheroni -konstanten optræder i Mertens tredje sætning og har relationer til gammafunktionen , zeta -funktionen og mange forskellige integraler og serier .

Det er endnu uvist, om det er rationelt eller ej. ${\ displaystyle \ gamma}$

Den numeriske værdi på er cirka 0,57721. ${\ displaystyle \ gamma}$

Conways konstante λ

{\ displaystyle {\ begin {matrix} 1 \\ 11 \\ 21 \\ 1211 \\ 111221 \\ 312211 \\\ vdots \ end {matrix}}}

Conway 's look-and-sige sekvens

Conways konstant er den invariante vækstrate for alle afledte strenge, der ligner look-and-say-sekvensen (undtagen en triviel).

Det er givet af den unikke positive reelle rod til et polynom af grad 71 med heltals koefficienter.

Værdien af λ er cirka 1.30357.

Khinchins konstante K

Hvis et reelt tal r er skrevet som en simpel fortsat brøk :

{\ displaystyle r = a_ {0}+{\ dfrac {1} {a_ {1}+{\ dfrac {1} {a_ {2}+{\ dfrac {1} {a_ {3}+\ cdots}} }}}},}

hvor a _k er naturlige tal for alle k , så, som den russiske matematiker Aleksandr Khinchin beviste i 1934, har grænsen som n tendens til uendelighed af det geometriske middelværdi : ( a ₁a ₂ ... a _n ) ^{1/ n} eksisterer og er en konstant, Khinchins konstant , bortset fra et sæt mål 0.

Den numeriske værdi af K er cirka 2,6854520010.

Glaisher - Kinkelin konstant A

Den Glaisher-Kinkelin konstant er defineret som grænsen :

{\ displaystyle A = \ lim _ {n \ rightarrow \ infty} {\ frac {\ prod _ {k = 1}^{n} k^{k}} {n^{n^{2}/2+n /2+1/12} e^{-n^{2}/4}}}}

Det er en vigtig konstant, der vises i mange udtryk for derivatet af Riemann zeta -funktionen . Den har en numerisk værdi på cirka 1,2824271291.

Matematiske nysgerrigheder og uspecificerede konstanter

Enkle repræsentanter for sæt numre

Denne babylonske lertavle giver en tilnærmelse af kvadratroden af 2 i fire seksagesimale tal: 1; 24, 51, 10, hvilket er nøjagtigt til omkring seks decimaler .

{\ displaystyle c = \ sum _ {j = 1}^{\ infty} 10^{-j!} = 0. \ underbrace {\ overbrace {110001}^{3! {\ text {digits}}} 000000000000000001}} _ {4! {\ Tekst {cifre}}} 000 \ prikker}

Liouvilles konstant er et enkelt eksempel på et transcendentalt tal .

Nogle konstanter, såsom kvadratroden af 2 , Liouvilles konstant og Champernowne -konstanten :

{\ displaystyle C_ {10} = 0. {\ color {blue} {1}} 2 {\ color {blue} {3}} 4 {\ color {blue} {5}} 6 {\ color {blue} { 7}} 8 {\ farve {blå} {9}} 10 {\ farve {blå} {11}} 12 {\ farve {blå} {13}} 14 {\ farve {blå} {15}} 16 \ prikker }

er ikke vigtige matematiske invarianter, men bevarer interessen som simple repræsentanter for særlige sæt tal, de irrationelle tal , de transcendentale tal og de normale tal (i basis 10). Opdagelsen af de irrationelle tal tilskrives normalt Pythagoras Hippasus fra Metapontum, der sandsynligvis geometrisk beviste irrationelheden af kvadratroden på 2. Hvad angår Liouvilles konstant, opkaldt efter den franske matematiker Joseph Liouville , var det det første tal, der var bevist transcendentalt.

Chaitins konstante Ω

I datalogi delfelt af algoritmisk informationsteori , Chaitin konstant er den virkelige tal, der repræsenterer sandsynligheden at en tilfældigt udvalgt Turing-maskine vil standse, dannet af en konstruktion på grund af argentinsk - amerikansk matematiker og datalog Gregory Chaitin . Chaitins konstante, selvom den ikke er beregningsbar , har vist sig at være transcendental og normal . Chaitins konstant er ikke universel, afhænger stærkt af den numeriske kodning, der bruges til Turing -maskiner; dens interessante egenskaber er imidlertid uafhængige af kodningen.

Uspecificerede konstanter

Når det ikke er specificeret, angiver konstanter klasser af lignende objekter, almindelige funktioner, der alle er lig med en konstant - teknisk set kan dette ses som 'lighed op til en konstant'. Sådanne konstanter forekommer ofte, når der er tale om integraler og differentialligninger . Selvom de ikke er specificeret, har de en bestemt værdi, som ofte ikke er vigtig.

Løsninger med forskellige konstanter for integration af .

{\ displaystyle y '(x) =-2y+e^{-x}}

I integraler

Ubestemte integraler kaldes ubestemt, fordi deres løsninger kun er unikke op til en konstant. For eksempel når man arbejder over feltet med reelle tal

{\ displaystyle \ int \ cos x \ dx = \ sin x+C}

hvor C , konstanten for integration , er et vilkårligt fast reelt tal. Med andre ord, uanset værdien af C giver differentiering sin x + C med hensyn til x altid cos x .

I differentialligninger

På lignende måde forekommer konstanter i løsningerne til differentialligninger, hvor der ikke gives tilstrækkelige startværdier eller randbetingelser . For eksempel har den almindelige differentialligning y ^' = y ( x ) løsning Ce ^x, hvor C er en vilkårlig konstant.

Når man beskæftiger sig med delvise differentialligninger , kan konstanterne være funktioner , konstante med hensyn til nogle variabler (men ikke nødvendigvis dem alle). For eksempel PDE

{\ displaystyle {\ frac {\ delvis f (x, y)} {\ delvis x}} = 0}

har løsninger f ( x , y ) = C ( y ), hvor C ( y ) er en vilkårlig funktion i variablen y .

Notation

Repræsenterer konstanter

Det er almindeligt at udtrykke den numeriske værdi af en konstant ved at give dens decimalrepræsentation (eller bare de første par cifre i den). Af to grunde kan denne fremstilling forårsage problemer. For det første, selvom rationelle tal alle har en endelig eller stadigt gentagende decimaludvidelse, har irrationelle tal ikke et sådant udtryk, hvilket gør dem umulige at beskrive fuldstændigt på denne måde. Desuden er decimaludvidelsen af et tal ikke nødvendigvis unik. For eksempel er de to repræsentationer 0.999 ... og 1 ækvivalente i den forstand, at de repræsenterer det samme tal.

Beregning af cifre i decimaludvidelse af konstanter har været en almindelig virksomhed i mange århundreder. For eksempel brugte den tyske matematiker Ludolph van Ceulen fra det 16. århundrede en stor del af sit liv på at beregne de første 35 cifre i pi. Ved hjælp af computere og supercomputere er nogle af de matematiske konstanter, herunder π, e og kvadratroden af 2, blevet beregnet til mere end hundrede milliarder cifre. Der er udviklet hurtige algoritmer , hvoraf nogle - som for Apérys konstant - er uventet hurtige.

{\ displaystyle G = \ left. {\ begin {matrix} 3 \ underbrace {\ uparrow \ ldots \ uparrow} 3 \\\ underbrace {\ vdots} \\ 3 \ uparrow \ uparrow \ uparrow \ uparrow 3 \ end {matrix }} \ højre \} {\ tekst {64 lag}}}

Grahams nummer defineret ved hjælp af Knuths pil op .

Nogle konstanter adskiller sig så meget fra den sædvanlige slags, at der er opfundet en ny notation for at repræsentere dem med rimelighed. Grahams nummer illustrerer dette, da Knuths op-pil-notation bruges.

Det kan være af interesse at repræsentere dem ved hjælp af fortsatte fraktioner til at udføre forskellige undersøgelser, herunder statistisk analyse. Mange matematiske konstanter har en analytisk form , det vil sige, at de kan konstrueres ved hjælp af velkendte operationer, der let kan beregnes. Ikke alle konstanter har imidlertid kendte analytiske former; Grossmans konstant og Foias konstant er eksempler.

Symbolisering og navngivning af konstanter

Symbolisering af konstanter med bogstaver er et hyppigt middel til at gøre notationen mere kortfattet. En almindelig konvention , der blev iværksat af René Descartes i 1600 -tallet og Leonhard Euler i 1700 -tallet, er at bruge små bogstaver fra begyndelsen af det latinske alfabet eller det græske alfabet, når det drejer sig om konstanter generelt. ${\ displaystyle a, b, c, \ dots}$ ${\ displaystyle \ alpha, \ beta, \, \ gamma, \ dots}$

For vigtigere konstanter kan symbolerne dog være mere komplekse og have et ekstra bogstav, en stjerne , et tal, et lemniscat eller bruge forskellige alfabeter som hebraisk , kyrillisk eller gotisk .

Erdős – Borwein konstant Embree – Trefethen konstant Bruns konstant for twin prime Champernowne konstanter kardinalnummer aleph nul

{\ displaystyle E_ {B}}

{\ displaystyle \ beta ^{*}}

{\ displaystyle B_ {2}}

{\ displaystyle C_ {b}}

{\ displaystyle \ aleph _ {0}}

Eksempler på forskellige former for notation for konstanter.

Nogle gange er symbolet, der repræsenterer en konstant, et helt ord. For eksempel opfandt den amerikanske matematiker Edward Kasners 9-årige nevø navnene googol og googolplex .

{\ displaystyle \ mathrm {googol} = 10^{100} \, \, \ \ mathrm {googolplex} = 10^{\ mathrm {googol}} = 10^{10^{100}}}

Andre navne er enten relateret til betydningen af konstanten ( universel parabolsk konstant , tvillingprimekonstant , ...) eller til en bestemt person ( Sierpińskis konstant , Josephson -konstant osv.).

Den universelle parabolske konstant er forholdet, for enhver parabel , af buelængden af det parabolske segment (rød) dannet af latus rectum (blå) til brændpunktsparameteren (grøn).

Tabel over udvalgte matematiske konstanter

Anvendte forkortelser:

R - rationelt tal , I - irrationelt tal (kan være algebraisk eller transcendentalt), A - algebraisk tal (irrationelt), T - transcendentalt tal (irrationelt)

Gen - Generelt , Nut - Antal teori , CHT - Kaos teori , Com - Kombinatorik , Inf - Information teori , Ana - Matematisk analyse

Symbol	Værdi	Navn	Mark	N	Først beskrevet	Antal kendte decimalcifre
0	= 0	Nul	Gen	R	af c. 500 f.Kr.	alle
1	= 1	En , enhed	Gen	R		alle
$jeg$	= $\sqrt -1$	Imaginær enhed , enhed imaginært nummer	Gen , Ana	EN	af c. 1500	alle
$π$	≈ 3.14159 26535 89793 23846 26433 83279 50288	Pi , Archimedes 'konstant eller Ludolphs nummer	Gen , Ana	T	af c. 2600 f.Kr.	62.831.853.071.796
$e$	≈ 2,71828 18284 59045 23536 02874 71352 66249	e , Napiers konstant eller Eulers nummer	Gen , Ana	T	1618	31.415.926.535.897
$\sqrt 2$	≈ 1.41421 35623 73095 04880 16887 24209 69807	Pythagoras 'konstant, kvadratrod af 2	Gen	EN	af c. 800 f.Kr.	10.000.000.000.000
$\sqrt 3$	≈ 1.73205 08075 68877 29352 74463 41505 87236	Theodorus konstant, kvadratrod af 3	Gen	EN	af c. 800 f.Kr.	2.199.023.255.552
$\sqrt 5$	23 2,23606 79774 99789 69640 91736 68731 27623	kvadratrod af 5	Gen	EN	af c. 800 f.Kr.	2.199.023.255.552
${\ displaystyle \ gamma}$	77 0,57721 56649 01532 86060 65120 90082 40243	Euler – Mascheroni konstant	Gen , NuT		1735	600.000.000.100
${\ displaystyle \ varphi}$	≈ 1.61803 39887 49894 84820 45868 34365 63811	Gyldent snit	Gen	EN	af c. 200 f.Kr.	10.000.000.000.000
${\ displaystyle \ Lambda}$	${\ displaystyle 0 \ leq \ Lambda \ leq 0.2}$	de Bruijn – Newman konstant	NuT , Ana		1950	ingen
M ₁	≈ 0,26149 72128 47642 78375 54268 38608 69585	Meissel – Mertens konstant	Nød		1866 1874	8.010
${\ displaystyle \ beta}$	≈ 0,28016 94990 23869 13303	Bernsteins konstant	Ana
${\ displaystyle \ lambda}$	30 0,30366 30028 98732 65859 74481 21901 55623	Gauss – Kuzmin – Wirsing konstant	Com		1974	385
${\ displaystyle \ sigma}$	35 0,35323 63718 54995 98454 35165 50432 68201	Hafner – Sarnak – McCurley konstant	Nød		1993
L	≈ 0,5	Landau er konstant	Ana			1
Ω	67 0,56714 32904 09783 87299 99686 62210 35554	Omega konstant	Ana	T
${\ displaystyle \ lambda}$ , ${\ displaystyle \ mu}$	≈ 0,62432 99885 43550 87099 29363 83100 83724	Golomb – Dickman konstant	Com , NuT		1930 1964
	≈ 0,64341 05462	Cahens konstant		T	1891	4000
C ₂	≈ 0,66016 18158 46869 57392 78121 10014 55577	Twin prime konstant	Nød			5.020
	≈ 0,66274 34193 49181 58097 47420 97109 25290	Laplace grænse
${\ displaystyle \ beta}$ ^*	0,70258	Embree – Trefethen konstant	Nød
K	≈ 0,76422 36535 89220 66299 06987 31250 09232	Landau - Ramanujan konstant	Nød			30.010
B ₄	≈ 0,87058 838	Bruns konstante for prime quadruplets	Nød			8
K	≈ 0,91596 55941 77219 01505 46035 14932 38411	Catalansk er konstant	Com			1.000.000.001.337
B' _L	= 1	Legendre er konstant	Nød	R		alle
K	≈ 1.13198 824	Viswanath er konstant	Nød			8
${\ displaystyle \ zeta (3)}$	≈ 1.20205 69031 59594 28539 97381 61511 44999	Apéry er konstant		jeg	1979	1.200.000.000.100
${\ displaystyle \ lambda}$	≈ 1.30357 72690 34296 39125 70991 12152 55189	Conway er konstant	Nød	EN
${\ displaystyle \ theta}$	≈ 1.30637 78838 63080 69046 86144 92602 60571	Mills konstant	Nød		1947	6850
${\ displaystyle \ rho}$	≈ 1.32471 79572 44746 02596 09088 54478 09734	Plast konstant	Nød	EN	1928
${\ displaystyle \ mu}$	≈ 1,45136 92348 83381 05028 39684 85892 02744	Ramanujan – Soldner konstant	Nød	jeg		75.500
	45 1.45607 49485 82689 67139 95953 51116 54356	Backhouse er konstant
	1,46707 80794	Porter er konstant	Nød		1975
	39 1.53960 07178	Liebs firkantede iskonstant	Com	EN	1967
E _B	≈ 1.60669 51524 15291 76378 33015 23190 92458	Erdős – Borwein konstant	Nød	jeg
	≈ 1.70521 11401 05367 76428 85514 53434 50816	Niven er konstant	Nød		1969
B ₂	≈ 1.90216 05831 04	Brun er konstant for tvillingetal	Nød		1919	12
P ₂	≈ 2.29558 71493 92638 07403 42980 49189 49039	Universal parabolsk konstant	Gen	T
${\ displaystyle \ alpha}$	≈ 2,50290 78750 95892 82228 39028 73218 21578	Feigenbaum konstant	ChT
K	≈ 2.58498 17595 79253 21706 58935 87383 17116	Sierpiński er konstant
	≈ 2,68545 20010 65306 44530 97148 35481 79569	Khinchin er konstant	Nød		1934	7350
F	≈ 2,80777 02420 28519 36522 15011 86557 77293	Fransén – Robinson konstant	Ana
	≈ 3.27582 29187 21811 15978 76818 82453 84386	Lévy er konstant	Nød
${\ displaystyle \ psi}$	35 3.35988 56662 43177 55317 20113 02918 92717	Gensidig Fibonacci -konstant		jeg
${\ displaystyle \ delta}$	66 4.66920 16091 02990 67185 32038 20466 20161	Feigenbaum konstant	ChT		1975

Se også

Noter

eksterne links

Konstanter - fra Wolfram MathWorld
Invers symbolsk lommeregner (CECM, ISC) (fortæller dig, hvordan et givet tal kan konstrueres ud fra matematiske konstanter)
Online encyklopædi for heltalssekvenser (OEIS)
Simon Plouffes inverter
Steven Finchs side med matematiske konstanter (BROKEN LINK)
Steven R. Finch, " Mathematical Constants ," Encyclopedia of mathematics and its applications , Cambridge University Press (2003).
Xavier Gourdon og Pascal Sebahs side med tal, matematiske konstanter og algoritmer

Languages

In other projects

Matematisk konstant - Mathematical constant

Indhold

Grundlæggende matematiske konstanter

Archimedes 'konstante $π$

Den imaginære enhed $i$

Eulers nummer $e$

Pythagoras konstant $\sqrt 2$

Theodorus konstant $\sqrt 3$

Konstanter i avanceret matematik

Feigenbaum -konstanterne α og δ

Apérys konstante ζ (3)

Det gyldne snit $φ$

Euler – Mascheroni -konstanten y

Conways konstante λ

Khinchins konstante K

Glaisher - Kinkelin konstant A

Matematiske nysgerrigheder og uspecificerede konstanter

Enkle repræsentanter for sæt numre

Chaitins konstante Ω

Uspecificerede konstanter

I integraler

I differentialligninger

Notation

Repræsenterer konstanter

Symbolisering og navngivning af konstanter

Tabel over udvalgte matematiske konstanter

Se også

Noter

eksterne links

Languages

In other projects

Matematisk konstant - Mathematical constant

Grundlæggende matematiske konstanter

Archimedes 'konstante π

Den imaginære enhed i

Eulers nummer e

Pythagoras konstant √ 2

Theodorus konstant √ 3

Konstanter i avanceret matematik

Feigenbaum -konstanterne α og δ

Apérys konstante ζ (3)

Det gyldne snit φ

Euler – Mascheroni -konstanten y

Conways konstante λ

Khinchins konstante K

Glaisher - Kinkelin konstant A

Matematiske nysgerrigheder og uspecificerede konstanter

Enkle repræsentanter for sæt numre

Chaitins konstante Ω

Uspecificerede konstanter

I integraler

I differentialligninger

Notation

Repræsenterer konstanter

Symbolisering og navngivning af konstanter

Tabel over udvalgte matematiske konstanter

Se også

Noter

eksterne links

Archimedes 'konstante $π$

Den imaginære enhed $i$

Eulers nummer $e$

Pythagoras konstant $\sqrt 2$

Theodorus konstant $\sqrt 3$

Det gyldne snit $φ$