Rolles sætning - Rolle's theorem

Hvis en reelt værdsat funktion f er kontinuerlig på et lukket interval [ a , b ] , der kan differentieres på det åbne interval ( a , b ) og f  ( a ) = f  ( b ) , eksisterer der en c i det åbne interval ( a , b ) sådan at f  ′ ( c ) = 0 .

I calculus , Rolles sætning eller Rolle lemma væsentlige, at enhver real-værdsat differentiable funktion at opnår lig værdierne ved to forskellige punkter skal have mindst ét stationært punkt et sted mellem dem, det vil sige, et punkt, hvor den første afledede (hældningen på tangentlinje til funktionens graf) er nul. Sætningen er opkaldt efter Michel Rolle .

Standardversion af sætningen

Hvis en reelt værdsat funktion f er kontinuerlig på et korrekt lukket interval [ a ,  b ] , der kan differentieres på det åbne interval ( a , b ) og f  ( a ) = f  ( b ) , eksisterer der mindst en c i det åbne interval ( a , b ) sådan

${\ displaystyle f '(c) = 0}$.

Denne version af Rolles sætning bruges til at bevise middelværdisætningen , hvoraf Rolles sætning faktisk er et specielt tilfælde. Det er også grundlaget for beviset på Taylors sætning .

Historie

Selvom sætningen er opkaldt efter Michel Rolle , dækkede Rolle's bevis fra 1691 kun tilfældet med polynomiske funktioner. Hans bevis brugte ikke metoderne til differentialregning , som han på det tidspunkt i sit liv anså for at være fejlagtig. Sætningen blev først bevist af Cauchy i 1823 som en følge af et bevis på middelværdisætningen . Navnet "Rolles sætning" blev først brugt af Moritz Wilhelm Drobisch fra Tyskland i 1834 og af Giusto Bellavitis fra Italien i 1846.

Eksempler

Første eksempel

En halvcirkel med radius r .

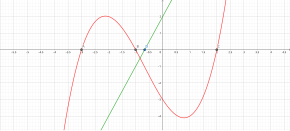
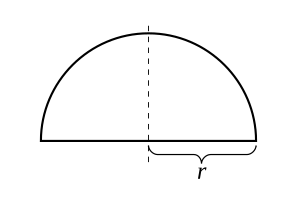
Overvej funktionen for en radius r > 0

${\ displaystyle f (x) = {\ sqrt {r^{2} -x^{2}}}, \ quad x \ in [-r, r].}$

Dens graf er den øverste halvcirkel centreret ved oprindelsen. Denne funktion er kontinuerlig på det lukkede interval [ - r , r ] og differentierbar i det åbne interval ( - r , r ) , men ikke differentierbar ved endepunkterne - r og r . Da f  ( - r ) = f  ( r ) , gælder Rolles sætning, og der er faktisk et punkt, hvor derivatet af f er nul. Bemærk, at sætningen gælder, selvom funktionen ikke kan differentieres ved endepunkterne, fordi den kun kræver, at funktionen er differentierbar i det åbne interval.

Andet eksempel

Grafen for funktionen absolut værdi.

Hvis differentieringen mislykkes på et internt punkt i intervallet, kan konklusionen på Rolles sætning muligvis ikke holde. Overveje den absolutte værdi funktion

${\ displaystyle f (x) = | x |, \ qquad x \ in [-1,1].}$

Så f  (−1) = f  (1) , men der er ingen c mellem −1 og 1, for hvilken f  ′ ( c ) er nul. Dette skyldes, at denne funktion, selvom den er kontinuerlig, ikke er differentierbar ved x = 0 . Bemærk, at derivatet af f ændrer sit tegn ved x = 0 , men uden at nå værdien 0. Sætningen kan ikke anvendes på denne funktion, fordi den ikke opfylder betingelsen om, at funktionen skal være differentierbar for hver x i det åbne interval. Når differentieringskravet falder fra Rolles sætning, vil f dog stadig have et kritisk tal i det åbne interval ( a , b ) , men det giver muligvis ikke en vandret tangens (som i tilfælde af den absolutte værdi, der er repræsenteret i grafen ).

Generalisering

Det andet eksempel illustrerer følgende generalisering af Rolles sætning:

Overvej en reelt værdsat, kontinuerlig funktion f på et lukket interval [ a , b ] med f  ( a ) = f  ( b ) . Hvis for hver x i det åbne interval ( a , b ) den højre grænse

${\ displaystyle f '(x^{+}): = \ lim _ {h \ til 0^{+}} {\ frac {f (x+h) -f (x)} {h}}}$

og venstre grænse

${\ displaystyle f '(x^{-}): = \ lim _ {h \ til 0^{-}} {\ frac {f (x+h) -f (x)} {h}}}$

findes i den udvidede reelle linje [−∞, ∞] , så er der et tal c i det åbne interval ( a , b ) sådan, at en af ​​de to grænser

${\ displaystyle f '(c^{+}) \ quad {\ text {og}} \ quad f' (c^{-})}$

er ≥ 0 og den anden er ≤ 0 (i den udvidede reelle linje). Hvis grænserne til højre og venstre er enige for hvert x , så er de især enige om c , derfor er derivatet af f ved c og er lig med nul.

Bemærkninger

• Hvis f er konveks eller konkave, findes der højre og venstre derivater på hvert indre punkt, derfor eksisterer ovenstående grænser og er reelle tal.
• Denne generaliserede version af sætningen er tilstrækkelig til at bevise konveksitet, når de ensidige derivater monotont stiger :

${\ displaystyle f '(x^{-}) \ leq f' (x^{+}) \ leq f '(y^{-}), \ qquad x <y.}$

Bevis for den generaliserede version

Da beviset for standardversionen af ​​Rolles sætning og generaliseringen er meget ens, beviser vi generaliseringen.

Idéen med beviset er at argumentere for, at hvis f  ( a ) = f  ( b ) , så skal f opnå et maksimum eller et minimum et sted mellem a og b , siger ved c , og funktionen skal ændre sig fra stigende til faldende ( eller omvendt) på c . Især hvis derivatet eksisterer, skal det være nul ved c .

Ved antagelse er f kontinuerlig på [ a , b ] , og ved ekstremværdisætningen når både sit maksimum og sit minimum i [ a , b ] . Hvis disse begge opnås ved endepunkterne for [ a , b ] , så f er konstant på [ a , b ] og så den afledede af f er nul i ethvert punkt i ( a , b ) .

Antag så, at maksimum opnås ved et indre punkt c på ( a , b ) (argumentet for minimum er meget ens, bare overvej - f  ). Vi skal undersøge ovenstående højre- og venstrehåndsgrænser separat.

For en reel h sådan, at c + h er i [ a , b ] , er værdien f  ( c + h ) mindre eller lig med f  ( c ), fordi f når sit maksimum ved c . Derfor, for hver h > 0 ,

${\ displaystyle {\ frac {f (c+h) -f (c)} {h}} \ leq 0,}$

derfor

${\ displaystyle f '(c^{+}): = \ lim _ {h \ til 0^{+}} {\ frac {f (c+h) -f (c)} {h}} \ leq 0 ,}$

hvor grænsen eksisterer ved antagelse, kan den være minus uendelig.

På samme måde vender uligheden for hver h <0 , fordi nævneren nu er negativ, og vi får

${\ displaystyle {\ frac {f (c+h) -f (c)} {h}} \ geq 0,}$

derfor

${\ displaystyle f '(c^{-}): = \ lim _ {h \ til 0^{-}} {\ frac {f (c+h) -f (c)} {h}} \ geq 0 ,}$

hvor grænsen kan være plus uendelig.

Endelig når ovenstående højre- og venstrehåndsgrænser stemmer overens (især når f er differentierbar), skal derivatet af f at c være nul.

(Alternativt kan vi anvende Fermats stationære punktssætning direkte.)

Generalisering til højere derivater

Vi kan også generalisere Rolles sætning ved at kræve, at f har flere point med lige værdier og større regelmæssighed. Antag det specifikt

• funktionen f er n - 1 gange kontinuerligt differentierbar på det lukkede interval [ a , b ], og n th -derivatet findes på det åbne interval ( a , b ) , og
• der er n intervaller givet med a ₁ < b ₁ ≤ a ₂ < b ₂ ≤ ... ≤ a _n < b _n i [ a , b ] således at f  ( a _k ) = f  ( b _k ) for hver k fra 1 til n .

Så er der et tal c i ( a , b ) sådan, at det n th afledte af f ved c er nul.

Den røde kurve er funktionsgrafen med 3 rødder i intervallet [−3, 2] . Således har dets andet derivat (tegnet i grønt) også en rod i det samme interval.

Kravene vedrørende n -derivatet af f kan svækkes som ved generaliseringen ovenfor, hvilket giver de tilsvarende (muligvis svagere) påstande for de højre og venstre grænser defineret ovenfor med f  ^{( n- 1)} i stedet for f .

Denne version af sætningen hævder især, at hvis en funktion, der kan differentieres nok gange har n rødder (så de har den samme værdi, det vil sige 0), så er der et internt punkt, hvor f  ^{( n - 1)} forsvinder.

Bevis

Beviset bruger matematisk induktion . Tilfældet n = 1 er simpelthen standardversionen af ​​Rolles sætning. For n > 1 antages induktionshypotesen, at generaliseringen er sand for n - 1 . Vi vil bevise det for n . Antag, at funktionen f opfylder teoremets hypoteser. Ved standardversionen af ​​Rolles sætning findes der for hvert heltal k fra 1 til n en c _k i det åbne interval ( a _k , b _k ) således at f  ′ ( c _k ) = 0 . Derfor opfylder det første derivat antagelserne om de n - 1 lukkede intervaller [ c ₁ , c ₂ ],…, [ c _{n - 1} , c _n ] . Ved induktionshypotesen er der en c, således at ( n - 1) st -derivatet af f  ′ at c er nul.

Generaliseringer til andre felter

Rolles sætning er en egenskab med differentierbare funktioner i forhold til de reelle tal, som er et ordnet felt . Som sådan generaliserer den ikke til andre felter , men følgende konsekvens gør: hvis et reelt polynom faktorer (har alle sine rødder) i forhold til de reelle tal, gør dets derivat det også. Man kan kalde denne ejendom for en mark Rolle ejendom . Mere generelle felter har ikke altid differentierbare funktioner, men de har altid polynomer, som symbolsk kan differentieres. På samme måde har mere generelle felter måske ikke en ordre, men man har en forestilling om en rod af et polynom, der ligger i et felt.

Således viser Rolles sætning, at de reelle tal har Rolles ejendom. Ethvert algebraisk lukket felt, såsom de komplekse tal, har Rolles ejendom. De rationelle tal har imidlertid ikke - for eksempel x ³ - x = x ( x - 1) ( x + 1) faktorer i forhold til rationelle , men dets derivat,

${\ displaystyle 3x^{2} -1 = 3 \ left (x-{\ tfrac {1} {\ sqrt {3}}} \ right) \ left (x+{\ tfrac {1} {\ sqrt {3} }}\ret),}$

gør ikke. Spørgsmålet om hvilke marker, der opfylder Rolle's ejendom, blev rejst i ( Kaplansky 1972 ). For begrænsede felter er svaret, at kun F ² og F ⁴ har Rolles ejendom.

For Voorhoeve -indekset for en kompleks version .

Se også

• Middelværdisætning
• Mellemværdisætning
• Lineær interpolation
• Gauss -Lucas sætning

Referencer

Yderligere læsning

• Leithold, Louis (1972). Beregningen med analytisk geometri (2. udgave). New York: Harper & Row. s. 201–207. ISBN 0-06-043959-9.
• Taylor, Angus E. (1955). Avanceret beregning . Boston: Ginn and Company. s. 30–37.

eksterne links

• "Rolle sætning" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Rolle- og middelværdisætninger ved cut-the-knot .
• Mizar system bevis: http://mizar.org/version/current/html/rolle.html#T2