Retlinje og kompas konstruktion -Straightedge and compass construction

Geometri
Projicering af en kugle til et fly
Omrids Historie
Grene Euklidisk Ikke-euklidisk Elliptisk Kugleformet Hyperbolsk Ikke-arkimedisk geometri Projektiv Affine Syntetisk Analytisk Algebraisk Aritmetik Diophantine Differential Riemannsk Symplektisk Diskret differential Kompleks Begrænset Diskret/kombinatorisk Digital Konveks Beregningsmæssig Fraktal Forekomst Ikke-kommutativ geometri Ikke-kommutativ algebraisk geometri
Begreber Funktioner Dimension Retlinje- og kompaskonstruktioner Vinkel Kurve Diagonal Ortogonalitet ( vinkelret ) Parallel Vertex overensstemmelsen Lighed Symmetri
Nuldimensional Punkt
Endimensionel Linje segment stråle Længde
Todimensionel Fly Areal Polygon Trekant Højde Hypotenuse Pythagoras sætning Parallelogram Firkant Rektangel Rhombus Rhomboid Firkantet Trapez Glente Cirkel Diameter Omkreds Areal
Tredimensionel Bind terning cuboid Cylinder Pyramide sfære
Fire- /andredimensionel Tesseract Hypersfære
Geometre
ved navn Aida Aryabhata Ahmes Alhazen Apollonius Archimedes Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Descartes Euklid Euler Gauss Gromov Hilbert Jyeṣṭhadeva Kātyāyana Khayyám Klein Lobachevsky Manava Minkowski Minggatu Pascal Pythagoras Parameshvara Poincaré Riemann Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Zhang Liste over geometre
efter periode fvt Ahmes Baudhayana Manava Pythagoras Euklid Archimedes Apollonius 1-1400-tallet Zhang Kātyāyana Aryabhata Brahmagupta Virasena Alhazen Sijzi Khayyám al-Yasamin al-Tusi Yang Hui Parameshvara 1400-1700-tallet Jyeṣṭhadeva Descartes Pascal Minggatu Euler Sakabe Aida 1700-1900-tallet Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter I dag Atiyah Gromov
v t e

Retlinje- og kompaskonstruktion , også kendt som lineal-og-kompas-konstruktion eller klassisk konstruktion , er konstruktionen af ​​længder, vinkler og andre geometriske figurer, der kun bruger en idealiseret lineal og et par kompasser .

Den idealiserede lineal, kendt som en straightedge , antages at være uendelig i længden, kun have én kant og ingen markeringer på den. Det antages, at kompasset ikke har nogen maksimum- eller minimumsradius, og det antages at "falde sammen", når det løftes fra siden, så det kan ikke bruges direkte til at overføre afstande. (Dette er en uvigtig begrænsning, da en afstand ved hjælp af en flertrinsprocedure kan overføres selv med et sammenfaldende kompas; se kompasækvivalenssætning . Bemærk dog, at mens et ikke-sammenfaldende kompas, der holdes mod en ligekant, kan synes at svare til markerer det, er neusis-konstruktionen stadig utilladelig, og dette er, hvad umarkeret virkelig betyder: se Markerbare linealer nedenfor.) Mere formelt er de eneste tilladte konstruktioner dem, der er givet af Euklids første tre postulater .

Det viser sig at være tilfældet, at ethvert punkt, der kan konstrueres ved hjælp af straightedge og kompas , også kan konstrueres ved hjælp af kompas alene , eller ved straightedge alene, hvis det gives en enkelt cirkel og dens centrum.

De gamle græske matematikere udtænkte først ligekant- og kompaskonstruktioner, og en række gamle problemer i plangeometri pålægger denne begrænsning. De gamle grækere udviklede mange konstruktioner, men var i nogle tilfælde ude af stand til det. Gauss viste, at nogle polygoner er konstruerbare, men at de fleste ikke er det. Nogle af de mest berømte problemer med straightedge og kompas blev bevist umulige af Pierre Wantzel i 1837, ved hjælp af den matematiske teori om felter .

På trods af eksisterende beviser for umulighed , fortsætter nogle med at forsøge at løse disse problemer. Mange af disse problemer er lette at løse, forudsat at andre geometriske transformationer er tilladt: for eksempel er fordobling af terningen muligt ved hjælp af geometriske konstruktioner, men ikke muligt ved brug af lige og kompas alene.

Med hensyn til algebra er en længde konstruerbar, hvis og kun hvis den repræsenterer et konstruerbart tal , og en vinkel er konstruerbar, hvis og kun hvis dens cosinus er et konstruerbart tal. Et tal kan konstrueres, hvis og kun hvis det kan skrives ved hjælp af de fire grundlæggende aritmetiske operationer og udtrækning af kvadratrødder , men uden rødder af højere orden.

Rette- og kompasværktøjer

"Straightedge" og "compass" af straightedge og kompaskonstruktioner er idealiseringer af linealer og kompasser i den virkelige verden:

• Rettekanten er uendelig lang, men den har ingen markeringer på sig og har kun én lige kant, i modsætning til almindelige linealer . Den tegnede linje er uendeligt tynd punktbredde. Den kan kun bruges til at tegne et linjestykke mellem to punkter, med uendelig præcision til disse punkter, eller til at udvide et eksisterende stykke.
• Kompasset kan åbnes vilkårligt bredt, men (i modsætning til nogle rigtige kompasser ) har det ingen markeringer på sig. Cirkler kan kun tegnes med udgangspunkt i to givne punkter: midten og et punkt på cirklen, og justeres til disse punkter med uendelig præcision. Buen der tegnes er uendeligt tynd punktbredde. Kompasset kan eller måske ikke kollapse, når det ikke tegner en cirkel.

Faktiske kompasser falder ikke sammen, og moderne geometriske konstruktioner bruger ofte denne funktion. Et 'sammenfaldende kompas' ser ud til at være et mindre kraftfuldt instrument. Ved kompasækvivalenssætningen i sætning 2 i bog 1 i Euklids elementer går der imidlertid ingen kraft tabt ved at bruge et sammenfaldende kompas. Selvom forslaget er korrekt, har dets beviser en lang og broget historie. Under alle omstændigheder er ækvivalensen grunden til, at denne funktion ikke er fastsat i definitionen af ​​det ideelle kompas.

Hver konstruktion skal være nøjagtig . Det tæller ikke som en løsning at "søge" det (i det væsentlige at se på konstruktionen og gætte på dens nøjagtighed, eller bruge en form for måling, såsom måleenhederne på en lineal) og komme tæt på.

Hvert byggeri skal ophøre . Det vil sige, at den skal have et begrænset antal trin og ikke være grænsen for stadig tættere tilnærmelser.

Udtrykt på denne måde ser ligekant- og kompaskonstruktioner ud til at være et salonspil snarere end et alvorligt praktisk problem; men formålet med begrænsningen er at sikre, at konstruktioner kan bevises at være helt rigtige.

Historie

De antikke græske matematikere forsøgte først ligekant- og kompaskonstruktioner, og de opdagede, hvordan man konstruerede summer , forskelle , produkter , forhold og kvadratrødder af givne længder. De kunne også konstruere halvdelen af ​​en given vinkel , et kvadrat, hvis areal er det dobbelte af et andet kvadrat, et kvadrat med samme areal som en given polygon og en regulær polygon med 3, 4 eller 5 sider (eller en med to gange antal sider af en given polygon). Men de kunne ikke konstruere en tredjedel af en given vinkel undtagen i særlige tilfælde, eller en firkant med samme areal som en given cirkel, eller en regulær polygon med andre antal sider. De kunne heller ikke konstruere siden af ​​en terning, hvis volumen ville være dobbelt så stor som en terning med en given side.

Hippokrates og Menaechmus viste, at rumfanget af kuben kunne fordobles ved at finde skæringspunkterne mellem hyperbler og parabler , men disse kan ikke konstrueres ved ligekant og kompas. I det femte århundrede f.v.t. brugte Hippias en kurve, som han kaldte en firkant til både at tredele den generelle vinkel og kvadratisk cirklen, og Nicomedes i det andet århundrede f.v.t. viste, hvordan man bruger en conchoid til at tredele en vilkårlig vinkel; men disse metoder kan heller ikke følges med kun ligekant og kompas.

Der blev ikke gjort fremskridt med de uløste problemer i to årtusinder, indtil Gauss i 1796 viste, at en regulær polygon med 17 sider kunne konstrueres; fem år senere viste han det tilstrækkelige kriterium for, at en regulær polygon på n sider kunne konstrueres.

I 1837 offentliggjorde Pierre Wantzel et bevis på umuligheden af ​​at tredele en vilkårlig vinkel eller fordoble rumfanget af en terning, baseret på umuligheden af ​​at konstruere terningrødder af længder. Han viste også, at Gauss' tilstrækkelige konstruerbarhedsbetingelse for regulære polygoner også er nødvendig.

Så i 1882 viste Lindemann , at det er et transcendentalt tal , og dermed at det er umuligt ved hjælp af lige og kompas at konstruere et kvadrat med samme areal som en given cirkel. ${\displaystyle \pi }$

De grundlæggende konstruktioner

Alle rette- og kompaskonstruktioner består af gentagen anvendelse af fem grundlæggende konstruktioner ved hjælp af de punkter, linjer og cirkler, der allerede er blevet konstrueret. Disse er:

• Oprettelse af linjen gennem to eksisterende punkter
• Oprettelse af cirklen gennem et punkt med midten af ​​et andet punkt
• Oprettelse af punktet, som er skæringspunktet mellem to eksisterende, ikke-parallelle linjer
• Oprettelse af et eller to punkter i skæringspunktet mellem en linje og en cirkel (hvis de skærer hinanden)
• Oprettelse af et eller to punkter i skæringspunktet mellem to cirkler (hvis de skærer hinanden).

For eksempel, startende med kun to forskellige punkter, kan vi oprette en linje eller en af ​​to cirkler (på skift ved at bruge hvert punkt som centrum og passere gennem det andet punkt). Hvis vi tegner begge cirkler, skabes to nye punkter ved deres skæringspunkter. Tegning af linjer mellem de to oprindelige punkter og et af disse nye punkter fuldender konstruktionen af ​​en ligesidet trekant.

Derfor har vi i ethvert geometrisk problem et indledende sæt af symboler (punkter og linjer), en algoritme og nogle resultater. Fra dette perspektiv svarer geometri til en aksiomatisk algebra , der erstatter dens elementer med symboler. Sandsynligvis indså Gauss dette først og brugte det til at bevise umuligheden af ​​nogle konstruktioner; først meget senere fandt Hilbert et komplet sæt aksiomer for geometri .

Meget brugte ligekant- og kompaskonstruktioner

De mest brugte ligekant- og kompaskonstruktioner inkluderer:

• Konstruktion af den vinkelrette halveringslinje ud fra et segment
• Finde midtpunktet af et segment.
• Tegning af en vinkelret linje fra et punkt til en linje.
• Halver en vinkel
• Spejling af et punkt i en linje
• Konstruere en linje gennem et punkt, der tangerer en cirkel
• Konstruktion af en cirkel gennem 3 ikke-kollineære punkter
• Tegning af en linje gennem et givet punkt parallelt med en given linje.

Konstruerbare punkter

Retlinje- og kompaskonstruktioner svarende til algebraiske operationer
x = a · b   (skæringssætning)	x = a / b   (skæringssætning)	x = √ a   (Pythagores sætning)

Man kan knytte en algebra til vores geometri ved hjælp af et kartesisk koordinatsystem lavet af to linjer og repræsentere punkter i vores plan ved hjælp af vektorer . Endelig kan vi skrive disse vektorer som komplekse tal.

Ved hjælp af ligningerne for linjer og cirkler kan man vise, at de punkter, hvor de skærer hinanden, ligger i en kvadratisk forlængelse af det mindste felt F , der indeholder to punkter på linjen, cirklens centrum og cirklens radius. Det vil sige, at de har formen x + y √ k , hvor x , y og k er i F .

Da feltet af konstruerbare punkter er lukket under kvadratrødder , indeholder det alle punkter, der kan opnås ved en endelig række af kvadratiske forlængelser af feltet af komplekse tal med rationelle koefficienter. Ved ovenstående afsnit kan man vise, at ethvert konstruerbart punkt kan opnås ved en sådan sekvens af forlængelser. Som en følge af dette finder man, at graden af ​​det minimale polynomium for et konstruerbart punkt (og derfor af enhver konstruerbar længde) er en potens af 2. Især ethvert konstruerbart punkt (eller længde) er et algebraisk tal , dog ikke hvert algebraisk tal er konstruerbart; for eksempel er ³ √ 2 algebraisk, men ikke konstruerbar.

Konstruerbare vinkler

Der er en bijektion mellem de vinkler, der er konstruerbare, og de punkter, der er konstruerbare på enhver konstruerbar cirkel. De vinkler, der er konstruerbare, danner en abelsk gruppe under addition modulo 2π (som svarer til multiplikation af punkterne på enhedscirklen set som komplekse tal). De vinkler, der er konstruerbare, er præcis dem, hvis tangent (eller tilsvarende sinus eller cosinus) kan konstrueres som et tal. For eksempel er den regulære heptadekagon (den syttensidede regulære polygon ) konstruerbar pga.

${\displaystyle \cos {\left({\frac {2\pi }{17}}\right)}=-{\frac {1}{16}}\;+\;{\frac {1}{16 }}{\sqrt {17}}\;+\;{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\;+\;{\frac {1 }{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17 }}}}}}}$

som opdaget af Gauss .

Gruppen af ​​konstruerbare vinkler lukkes under operationen, der halverer vinkler (hvilket svarer til at tage kvadratrødder i de komplekse tal). De eneste vinkler af endelig rækkefølge, der kan konstrueres begyndende med to punkter, er dem, hvis rækkefølge er enten en potens af to eller et produkt af en potens af to og et sæt af forskellige Fermat-primtal . Derudover er der et tæt sæt af konstruerbare vinkler af uendelig rækkefølge.

Relation til kompleks aritmetik

Givet et sæt af punkter i det euklidiske plan , gør det at vælge et af dem til at blive kaldt 0 og et andet til at blive kaldt 1 , sammen med et vilkårligt valg af orientering, det giver os mulighed for at betragte punkterne som et sæt af komplekse tal .

Givet enhver sådan fortolkning af et sæt punkter som komplekse tal, er de punkter, der kan konstrueres ved brug af gyldige ligekant- og kompaskonstruktioner alene, netop elementerne i det mindste felt, der indeholder det oprindelige sæt af punkter og lukket under de komplekse konjugat- og kvadratrodsoperationer (for at undgå tvetydighed, kan vi angive kvadratroden med komplekst argument mindre end π). Elementerne i dette felt er netop dem, der kan udtrykkes som en formel i de oprindelige punkter ved kun at bruge operationerne addition , subtraktion , multiplikation , division , kompleks konjugat og kvadratrod , som let kan ses som en tællig tæt delmængde af flyet. Hver af disse seks operationer svarer til en simpel rette- og kompaskonstruktion. Ud fra en sådan formel er det ligetil at fremstille en konstruktion af det tilsvarende punkt ved at kombinere konstruktionerne for hver af de aritmetiske operationer. Mere effektive konstruktioner af et bestemt sæt af punkter svarer til genveje i sådanne beregninger.

Tilsvarende (og uden behov for vilkårligt at vælge to punkter) kan vi sige, at givet et vilkårligt valg af orientering, bestemmer et sæt punkter et sæt komplekse forhold givet ved forholdet mellem forskellene mellem to vilkårlige par af punkter. Sættet af forhold, der kan konstrueres ved hjælp af straightedge og kompas fra et sådant sæt af forhold, er netop det mindste felt, der indeholder de oprindelige forhold og lukket under at tage komplekse konjugater og kvadratrødder.

For eksempel kan den reelle del, imaginære del og modul af et punkt eller forhold z (ved at tage et af de to synspunkter ovenfor) konstrueres, da disse kan udtrykkes som

${\displaystyle \mathrm {Re} (z)={\frac {z+{\bar {z}}}{2}}\;}$

${\displaystyle \mathrm {Im} (z)={\frac {z-{\bar {z}}}{2i}}\;}$

${\displaystyle \left|z\right|={\sqrt {z{\bar {z}}}}.\;}$

Fordobling af terningen og tredelingen af ​​en vinkel (bortset fra specielle vinkler, såsom enhver φ , sådan at φ /2π er et rationelt tal med nævneren ikke delelig med 3) kræver forhold, som er løsningen til kubiske ligninger , mens kvadrering af cirklen kræver en transcendental forhold. Ingen af ​​disse er i de beskrevne felter, hvorfor der ikke eksisterer nogen rette- og kompaskonstruktion for disse.

Umulige konstruktioner

De gamle grækere troede, at de byggeproblemer, de ikke kunne løse, simpelthen var stædige, ikke uløselige. Med moderne metoder har disse ligekant- og kompaskonstruktioner dog vist sig at være logisk umulige at udføre. (Problemerne i sig selv er imidlertid løselige, og grækerne vidste, hvordan de skulle løse dem uden begrænsningen af ​​kun at arbejde med lige og kompas.)

Kvadring af cirklen

Det mest berømte af disse problemer, kvadratur af cirklen , ellers kendt som cirklens kvadratur, involverer at konstruere en firkant med det samme areal som en given cirkel ved kun at bruge lige og kompas.

Kvadring af cirklen har vist sig umuligt, da det involverer generering af et transcendentalt tal , det vil sige √ π . Kun visse algebraiske tal kan konstrueres med lineal og kompas alene, nemlig dem, der er konstrueret ud fra heltal med en endelig række af operationer med addition, subtraktion, multiplikation, division og at tage kvadratrødder. Udtrykket "squaring the circle" bruges ofte til at betyde "at gøre det umulige" af denne grund.

Uden begrænsningen af ​​at kræve løsning med lineal og kompas alene, er problemet let løses ved en bred vifte af geometriske og algebraiske midler, og blev løst mange gange i antikken.

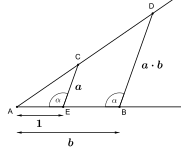
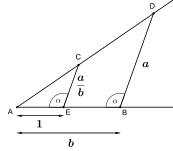
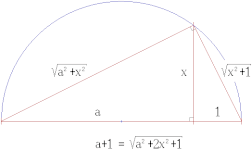
En metode, der kommer meget tæt på at tilnærme "cirklens kvadratur" kan opnås ved hjælp af en Kepler-trekant .

Fordobling af terningen

Fordobling af terningen er konstruktionen, kun ved hjælp af en lige kant og kompas, af kanten af ​​en terning, der har dobbelt så stor volumen som en terning med en given kant. Dette er umuligt, fordi terningroden af ​​2, selvom den er algebraisk, ikke kan beregnes ud fra heltal ved addition, subtraktion, multiplikation, division og at tage kvadratrødder. Dette følger, fordi dets minimale polynomium over rationalerne har grad 3. Denne konstruktion er mulig ved at bruge en ligekant med to mærker på og et kompas.

Vinkel tresektion

Vinkeltrisektion er konstruktionen af ​​en vinkel, der er en tredjedel af en given vilkårlig vinkel, kun ved hjælp af en ligekant og et kompas. Dette er umuligt i det generelle tilfælde. For eksempel kan vinklen 2π/5 radianer (72° = 360°/5) tredeles, men vinklen på π/3 radianer (60 ° ) kan ikke tredeles. Det generelle tresektionsproblem løses også nemt, når en rettekant med to mærker på er tilladt (en neusis- konstruktion).

Afstand til en ellipse

Linjestykket fra ethvert punkt i planet til det nærmeste punkt på en cirkel kan konstrueres, men segmentet fra ethvert punkt i planet til det nærmeste punkt på en ellipse med positiv excentricitet kan generelt ikke konstrueres.

Alhazens problem

I 1997 beviste Oxford - matematikeren Peter M. Neumann sætningen om, at der ikke er nogen lineal-og-kompas-konstruktion til den generelle løsning af det gamle Alhazens problem (billardproblem eller refleksion fra et sfærisk spejl).

Konstruktion af regulære polygoner

Nogle regulære polygoner (f.eks. en femkant ) er nemme at konstruere med ligekant og kompas; andre er ikke. Dette førte til spørgsmålet: Er det muligt at konstruere alle regulære polygoner med straightedge og kompas?

Carl Friedrich Gauss i 1796 viste, at en regulær 17-sidet polygon kan konstrueres, og fem år senere viste, at en regulær n - sidet polygon kan konstrueres med ligekant og kompas, hvis de ulige primfaktorer af n er distinkte Fermat-primtal . Gauss formodede , at denne betingelse også var nødvendig , men han fremlagde intet bevis for dette faktum, som blev leveret af Pierre Wantzel i 1837.

De første par konstruerbare regulære polygoner har følgende antal sider:

3 , 4 , 5 , 6 , 8 , 10 , 12 , 15 , 16 , 17 , 20 , 24 , 30 , 32 , 34 , 40 , 48 , 51 , 60 , 64 , 0 , 8 , 6 , 8 , 6 120 , 128, 136, 160, 170, 192, 204, 240, 255, 256, 257 , 272... (sekvens A003401 i OEIS )

Der vides at være en uendelighed af konstruerbare regulære polygoner med et lige antal sider (fordi hvis en regulær n -gon er konstruerbar, så er en regulær 2 n -gon det samme og dermed en regulær 4 n -gon, 8 n -gon , etc.). Der er dog kun 31 kendte konstruerbare regulære n -goner med et ulige antal sider.

Konstruktion af en trekant ud fra tre givne karakteristiske punkter eller længder

Seksten nøglepunkter i en trekant er dens spidser , midtpunkterne på dens sider , fødderne af dens højder , fødderne af dens indre vinkelhalveringslinjer og dens circumcenter , tyngdepunkt , ortocenter og incenter . Disse kan tages tre ad gangen for at give 139 distinkte ikke-trivielle problemer med at konstruere en trekant fra tre punkter. Af disse problemer involverer tre et punkt, der entydigt kan konstrueres ud fra de to andre punkter; 23 kan være ikke-unik konstrueret (faktisk for uendeligt mange løsninger), men kun hvis placeringerne af punkterne overholder visse begrænsninger; i 74 er problemet konstruerbart i det generelle tilfælde; og i 39 eksisterer den nødvendige trekant, men er ikke konstruerbar.

Tolv nøglelængder af en trekant er de tre sidelængder, de tre højder , de tre medianer og de tre vinkelhalveringslinjer . Sammen med de tre vinkler giver disse 95 distinkte kombinationer, hvoraf 63 giver anledning til en konstruerbar trekant, hvoraf 30 ikke gør det, og to af dem er underdefinerede.

Begrænsede konstruktioner

Der er gjort forskellige forsøg på at begrænse de tilladte værktøjer til konstruktioner under forskellige regler, for at afgøre, hvad der stadig kan konstrueres, og hvordan det må konstrueres, samt fastlægge de minimumskriterier, der er nødvendige for stadig at kunne konstruere alt, der passer og rette kan.

Konstruktion med kun lineal eller kun kompas

Det er muligt (ifølge Mohr-Mascheroni-sætningen ) at konstruere hvad som helst med kun et kompas, hvis det kan konstrueres med en lineal og kompas, forudsat at de givne data og de data, der skal findes, består af diskrete punkter (ikke linjer eller cirkler) ). Sandheden af ​​denne sætning afhænger af sandheden af ​​Archimedes' aksiom , som ikke er af første orden. Eksempler på kompaskonstruktioner omfatter Napoleons problem .

Det er umuligt at tage en kvadratrod med kun en lineal, så nogle ting, der ikke kan konstrueres med en lineal, kan konstrueres med et kompas; men (ved Poncelet-Steiner-sætningen ) givet en enkelt cirkel og dens centrum, kan de konstrueres.

Udvidede konstruktioner

De gamle grækere klassificerede konstruktioner i tre hovedkategorier, afhængigt af kompleksiteten af ​​de nødvendige værktøjer til deres løsning. Hvis en konstruktion kun brugte en rettekant og kompas, blev den kaldt plan; hvis det også krævede et eller flere keglesnit (andre end cirklen), så blev det kaldt solidt; den tredje kategori omfattede alle konstruktioner, der ikke faldt ind under nogen af ​​de to andre kategorier. Denne kategorisering passer fint ind i det moderne algebraiske synspunkt. Et komplekst tal, der kun kan udtrykkes ved brug af feltoperationer og kvadratrødder (som beskrevet ovenfor ) har en plan konstruktion. Et komplekst tal, der også omfatter udvinding af terningrødder, har en solid konstruktion.

I felternes sprog har et komplekst tal, der er plant, grad en potens af to, og ligger i en feltudvidelse , der kan opdeles i et tårn af felter, hvor hver udvidelse har grad to. Et komplekst tal, der har en solid konstruktion, har grad med primfaktorer på kun to og tre, og ligger i en feltudvidelse, der er i toppen af ​​et tårn af felter, hvor hver udvidelse har grad 2 eller 3.

Solide konstruktioner

Et punkt har en solid konstruktion, hvis det kan konstrueres ved hjælp af en straightedge, et kompas og et (eventuelt hypotetisk) kegletegneværktøj, der kan tegne enhver kegle med allerede konstrueret fokus, retning og excentricitet. Det samme sæt punkter kan ofte konstrueres ved hjælp af et mindre sæt værktøjer. For eksempel ved hjælp af et kompas, en ligekant og et stykke papir, hvorpå vi har parablen y=x ² sammen med punkterne (0,0) og (1,0), kan man konstruere et hvilket som helst komplekst tal, der har et fast stof konstruktion. Ligeledes er et værktøj, der kan tegne enhver ellipse med allerede konstruerede foci og storakse (tænk to stifter og et stykke snor), lige så kraftfuldt.

De gamle grækere vidste, at fordobling af terningen og tredeling af en vilkårlig vinkel begge havde solide konstruktioner. Archimedes gav en solid konstruktion af den almindelige 7-gon. Cirklens kvadratur har ikke en solid konstruktion.

En regulær n -gon har en solid konstruktion, hvis og kun hvis n =2 ^j 3 ^k m hvor m er et produkt af forskellige Pierpont-primtal (primtal på formen 2 ^r 3 ^s +1). Mængden af ​​sådanne n er rækkefølgen

7 , 9 , 13 , 14 , 18 , 19 , 21 , 26, 27, 28, 35, 36, 37, 38, 39, 42 , 45, 52, 54, 56, 57, 63, 0, 7, 6 73, 74, 76, 78, 81, 84, 90, 91, 95, 97... (sekvens A051913 i OEIS )

Mængden af ​​n , for hvilken en regulær n -gon ikke har nogen solid konstruktion, er rækkefølgen

11 , 22 , 23 , 25, 29, 31, 33, 41, 43, 44, 46, 47, 49, 50, 53, 55, 58, 59, 61, 62, 66, 67, 69, 71, 77, 79, 82, 83, 86, 87, 88, 89, 92, 93, 94, 98, 99, 100... (sekvens A048136 i OEIS )

Ligesom spørgsmålet med Fermat-primtal er det et åbent spørgsmål, om der er et uendeligt antal Pierpont-primtal.

Vinkel tresektion

Hvad hvis vi sammen med rettekanten og kompasset havde et værktøj, der (kun) kunne tredele en vilkårlig vinkel? Sådanne konstruktioner er solide konstruktioner, men der findes tal med solide konstruktioner, som ikke kan konstrueres ved hjælp af et sådant værktøj. For eksempel kan vi ikke fordoble terningen med sådan et værktøj. På den anden side kan enhver almindelig n-gon, der har en solid konstruktion, konstrueres ved hjælp af et sådant værktøj.

Origami

Den matematiske teori om origami er mere kraftfuld end ligekant og kompaskonstruktion. Folder, der opfylder Huzita-Hatoris aksiomer, kan konstruere nøjagtigt det samme sæt punkter som de udvidede konstruktioner ved hjælp af et kompas og et kegletegneværktøj. Derfor kan origami også bruges til at løse kubiske ligninger (og dermed kvartære ligninger), og dermed løse to af de klassiske problemer.

Markable linealer

Archimedes , Nicomedes og Apollonius gav konstruktioner, der involverede brugen af ​​en markabel lineal. Dette ville tillade dem for eksempel at tage et linjestykke, to linjer (eller cirkler) og et punkt; og tegn derefter en linje, som går gennem det givne punkt og skærer de to givne linjer, sådan at afstanden mellem skæringspunkterne er lig med det givne segment. Dette kaldte grækerne neusis ("tilbøjelighed", "tendens" eller "skærende"), fordi den nye linje tenderer til punktet. I dette udvidede skema kan vi tredele en vilkårlig vinkel (se Arkimedes' tresnit ) eller udtrække en vilkårlig terningrod (på grund af Nicomedes). Derfor kan enhver afstand, hvis forhold til en eksisterende afstand er løsningen af ​​en kubisk eller en kvartsligning, konstrueres. Ved hjælp af en markérbar lineal kan regulære polygoner med solide konstruktioner, som sekskanten , konstrueres; og John H. Conway og Richard K. Guy giver konstruktioner til flere af dem.

Neusis-konstruktionen er kraftigere end et kegletegneværktøj, da man kan konstruere komplekse tal, der ikke har solide konstruktioner. Faktisk kan man ved at bruge dette værktøj løse nogle quintics, der ikke kan løses ved hjælp af radikaler . Det er kendt, at man ikke kan løse et irreducerbart polynomium af primegrad større eller lig med 7 ved hjælp af neusis-konstruktionen, så det er ikke muligt at konstruere en regulær 23-gon eller 29-gon ved hjælp af dette værktøj. Benjamin og Snyder beviste, at det er muligt at konstruere den almindelige 11-gon, men gav ikke en konstruktion. Det er stadig åbent om en almindelig 25-gon eller 31-gon kan konstrueres ved hjælp af dette værktøj.

Tredelt et lige segment

Givet et lige linjestykke kaldet AB, kunne dette opdeles i tre nye lige store segmenter og i mange dele krævet ved brug af skæringssætning

Beregning af binære cifre

I 1998 gav Simon Plouffe en lineal- og kompasalgoritme , der kan bruges til at beregne binære cifre af bestemte tal. Algoritmen involverer den gentagne fordobling af en vinkel og bliver fysisk upraktisk efter omkring 20 binære cifre.

Se også

• Carlyle cirkel
• Geometrisk kryptografi
• Geometri
• Liste over interaktiv geometrisoftware , de fleste af dem viser straightedge- og kompaskonstruktioner
• Matematik af papirfoldning
• Underwood Dudley , en matematiker, der har gjort en bibeskæftigelse med at indsamle falske rette- og kompasbeviser.

Referencer

eksterne links

• Regelmæssige polygonkonstruktioner af Dr. Math på Math Forum @ Drexel
• Konstruktion med kun kompasset ved klippe-knuden
• Vinkeltrisektion af Hippocrates ved klip-knuden
• Weisstein, Eric W. "Angle Trisection" . MathWorld .